适用于模块化多电平变换器的改进调制策略研究

姚骏，尹潇，赵磊，谭义

（重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044）

0 引 言

随着电力电子技术的飞速发展，多电平技术日渐发展成为一门完善的电力电子学科，并在电力系统中得到越来越多的应用［1］。在众多的多电平变换器中，模块化多电平变换器（Modular Multilevel Converter，MMC）由于其易于扩展、设计灵活等诸多优点，受到了国内外学者的广泛关注［2-4］。目前，针对MMC的研究重点主要集中在子模块电容均压控制［5-7］、调制策略［8-10］以及内部二倍频环流抑制［11-13］等方面，其中，调制策略需要解决是如何根据调制波得到开关器件的驱动触发信号的问题，以保证变换器输出目标电压。调制算法是电压源换流器的核心技术之一，算法直接决定了开关器件的通断状态，对变换器的电能转换性能有着十分重要的影响。

MMC的调制策略主要有载波移相调制（Carrier Phase Shifted，CPS）［6］和最近电平逼近调制（Nearest Level Modulation，NLM）［10］两种策略，CPS最早由Hagiwara M等人在文献［14］中提出，载波移相调制的优点在于可以利用较低的开关频率实现较高的等效开关频率，但CPS需要为每个子模块辅以专门的三角载波信号，对于一个三相全桥MMC，变换器每增加一个电平数，就需要增加6路载波信号，背靠背系统则需要增加12路载波信号，这就增加了系统的扩展难度。此外，根据文献［14］所述，为稳定子模块电容电压，需要为每个子模块配备专门的电压平均控制器和均衡控制器，进一步增加了系统的复杂程度。CPS本质上仍然属于脉冲宽度调制，而NLM调制算法不再依赖于载波信号，不再需要控制脉冲宽度，实现方法更为简单，因此更加容易适应MMC电平数的扩展。但当子模块数目较少时，用阶梯波逼近正弦调制波将带来较大的误差。对此，文献［15］提出一种将PWM调制与最近NLM调制相结合的改进调制策略，有效提高了MMC的输出电平数，降低了变换器输出电压的谐波含量，但由于引入了PWM调制，策略实现起来较为复杂。针对子模块数较少时NLM调制逼近误差大的问题，本文提出了一种改进调制策略，所提策略能够将变换器的输出电平数提高近1倍，减小调制策略的逼近误差，有效降低变换器的输出电压谐波含量。所提方法由于无需PWM调制，在工程实现方面更为简单。

1 MMC基本运行特性

1.1 MMC拓扑结构

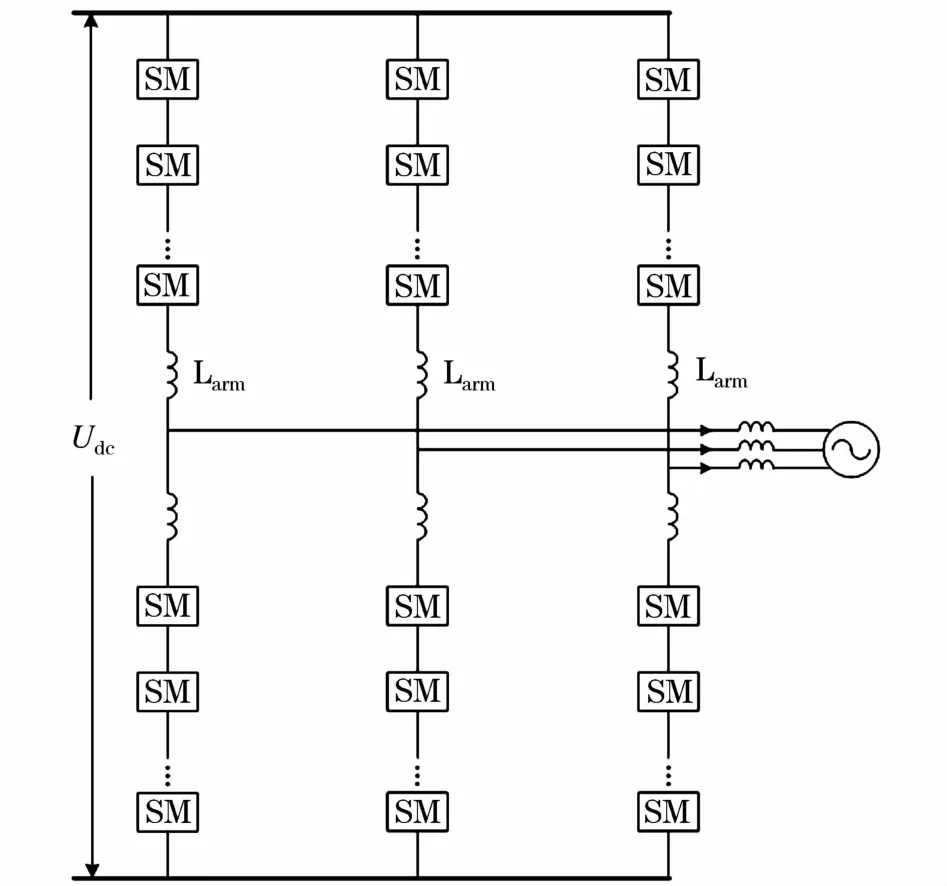
图1 模块化多电平变换器Fig.1 Modular multilevel converter

图1所示为三相MMC拓扑结构，变换器相单元包括上下两个桥臂，每个桥臂由若干子模块单元（submodules，SM）和一个桥臂电感Larm串联而成。在本文的研究中，子模块采用如图2所示的半桥型子模块，通过对两个开关器件T1、T2进行通断控制，可以使子模块投入到变换器桥臂中或者从桥臂中切除，从而使子模块输出电容电压uc和0两个电平。

子模块的具体工作状态如表1所示，当子模块投入到桥臂中时，子模块电容会由于桥臂电流方向不同而被充放电；当子模块从桥臂中切除时，电容被旁路，无论桥臂电流方向如何，电容电压保持不变。通过相应的调制算法对每个相单元内所有子模块的开关状态进行不同组合，便可使变换器在输出点输出幅值和频率可调的交流电压。

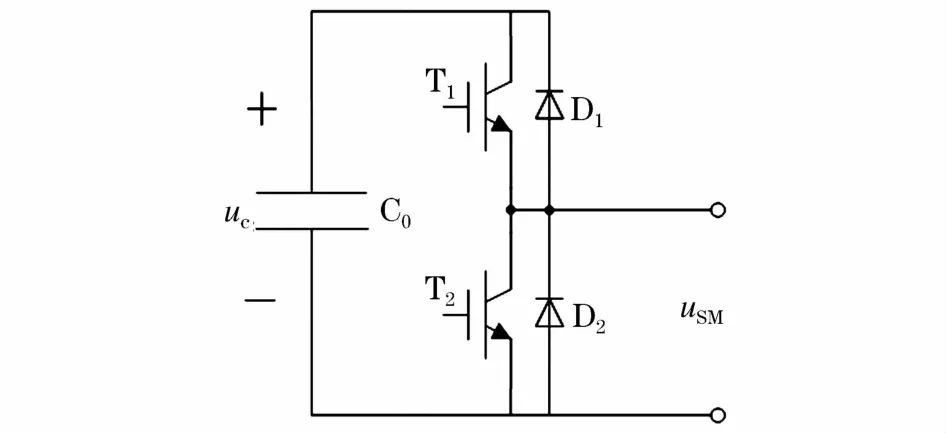
图2 模块化多电平变换器子模块拓扑结构图Fig.2 Topology structure diagram of sub-module of MMC

表1 子模块工作状态Tab.1 Working conditions of sub-modules

1.2 MMC工作原理

正常工作时，在均压算法的控制下，变换器所有子模块电容电压均维持均衡、稳定［5］；为维持直流母线电压的恒定，变换器每相单元均需要投入一定数量的子模块，以支撑直流母线电压［6］。通过在相单元上下桥臂中选择不同数目的子模块投入到桥臂，即可实现变换器交流侧不同电平的输出。由于变换器桥臂为子模块串联结构，由前述子模块的工作原理可知，选择不同数目的子模块投入到桥臂中，即可改变桥臂的整体输出电压，因此可将变换器的桥臂单元等效为一个受控电压源，如图3所示。

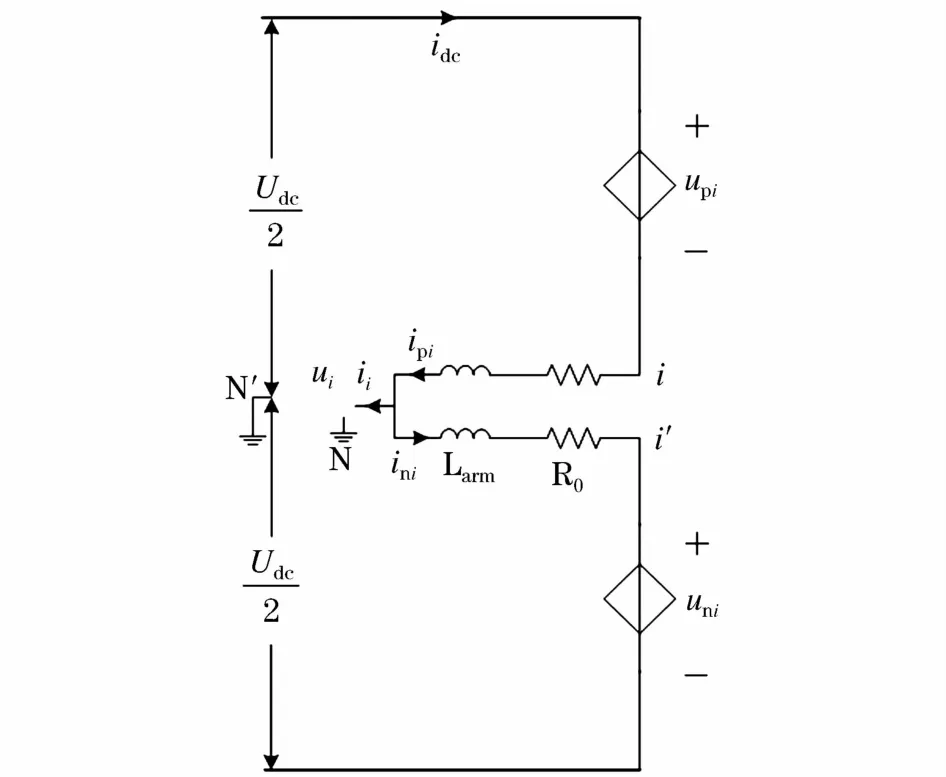
图3 模块化多电平变换器相单元平均等效电路Fig.3 Equivalent circuit of one phase of MMC

图3中，R0代表IGBT导通损耗和桥臂电抗杂散损耗的等效电阻，N和N′分别表示变换器交流侧中性点和假想的直流侧中性点，ui、ii（i=a，b，c，下同）分别表示变换器交流输出点的电压电流，ipi、ini为流过i相单元上下桥臂的电流，upi、uni分别表示i相单元上、下桥臂对外的整体输出电压。

应用基尔霍夫电压方程分析变换器上下桥臂可知，MMC相单元上下桥臂满足以下约束方程：

忽略变换器自身的损耗以及桥臂电感上的压降，则可根据式（1）得到桥臂参考电压 c计算表达式：

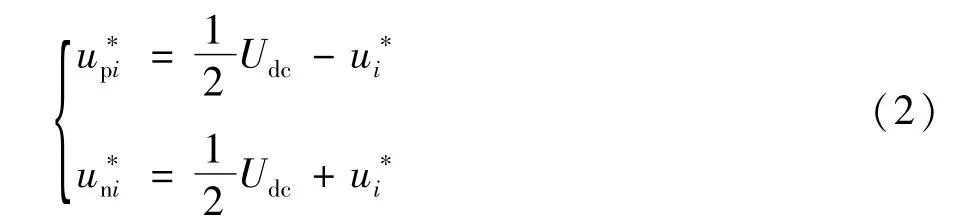
2 MMC调制策略分析

调制策略对MMC的换流性能有着至关重要的影响，目前，适用于MMC调制策略主要有载波移相调制和最近电平逼近调制两种策略。其中，载波移相调制需要为每个子模块设计相应的载波信号和专门的电压控制器，在一定程度上限制了变换器的扩展性能；而最近电平逼近调制过程则不需要依赖载波信号，由于省去了调制波与载波信号的比较调制过程，最近电平逼近调制的实现方法更为简单，更加容易实现变换器电平数的扩展。

2.1 传统最近电平逼近调制策略

在子模块电容电压维持稳定的前提下，选择不同数目的子模块投入到桥臂中即可改变变换器交流侧输出电平。最近电平逼近调制策略的基本思想是利用此特点用变换器的不同电平组成阶梯波去逼近等效正弦调制波。其具体调制过程为：首先利用调制波直接计算变换器各个桥臂需要投入的子模块数目，然后再根据子模块电容的均压算法最终确定各子模块的投入切除状态。

式中Ucref为子模块电容电压子模块电容电压参考值，对每个桥臂包含N个子模块的变换器，Ucref一般取值为Udc/N。根据式（2）、式（3）可改写为：

式中ui*是一个取值连续的变量，为得到整数的子模块数目，需要对式中右边第二项进行取整，常见的取整方法有向下取整 （floor）、向上取整 （cell）以及就近取整（round），一般常采用就近取整函数。因此，根据调制算法求得的上下桥臂需要投入到桥臂中的子模块数分别为：

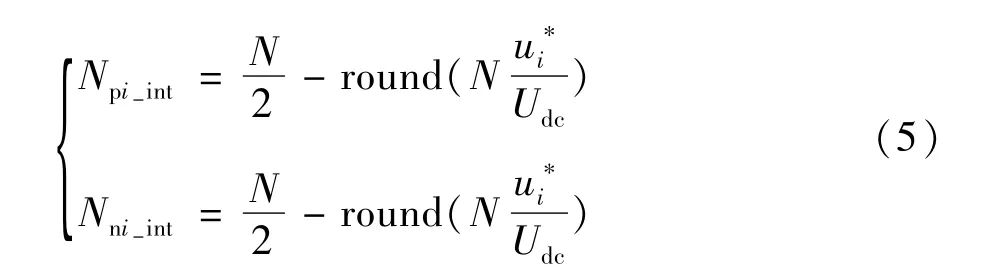
根据式（5）的计算结果，选择相应数目的子模块投入到变换器各桥臂中，即可在变流器的输出点得到逼近调制信号的阶梯波。

2.2 改进最近电平逼近调制策略

由2.1节论述可知，最近电平逼近调制过程只涉及了子模块数N一个参数，且不需要附加的控制器，具有很强的扩展性。但是当变换器包含的子模块数较少时，式（5）中的取整函数将带来较大的误差，影响阶梯波的逼近效果；表2列出了个子模块数为4的MMC变换器的基本工作状态，图4所示为此时利用阶梯波代替正弦调制波的逼近效果。

表2 包含4个子模块的MMC工作状态表Tab.2 Work status table of MMC including 4 sub-modules

由图4可知，电平数较低时，用阶梯波代替正弦波会产生比较大的误差，输出阶梯波由于电平数较少，相邻电平之间的电压差较大，对正弦调制波逼近效果有限，谐波含量大。对每个桥臂包含N个子模块的MMC，在保持每相单元上下桥臂投入子模块总数Nin固定为N的情况下，变换器交流侧最多可输出N+1个电平。

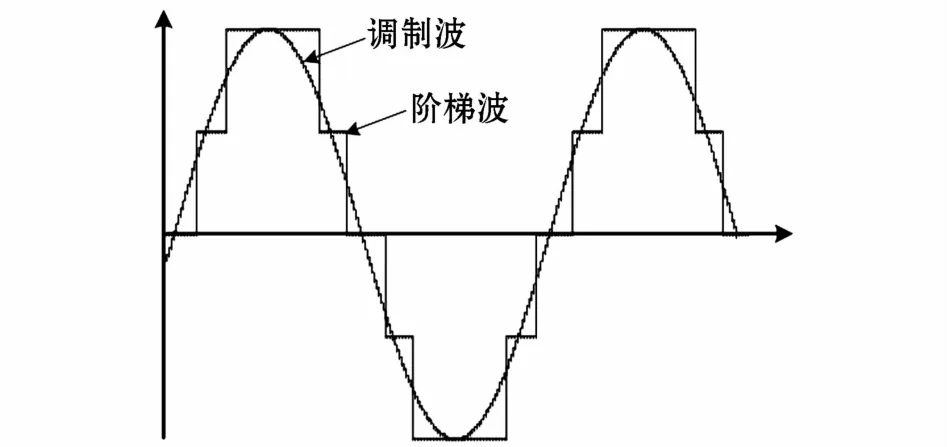
图4 子模块数为4时最近电平逼近调制结果Fig.4 NLM result of MMC with 4 sub-modules

为提高变换器的输出电平数，文献［15］提出了一种将最近电平逼近调制和PWM相结合的改进调制策略，采用该策略调制时，Nin不再固定为N；采用文献［14］中的载波移相调制策略时，变换器的输出电平数为2N+1，该策略对应的Nin也不是始终保持为N。由此可见，适当改变变换器相单元上下桥臂投入子模块总数Nin在某些情况下可以提高变换器的输出性能。按此思路，针对本文提出一种改变相单元投入子模块总数的改进型调制策略，以改善变换器包含子模块数较少时最近电平调制的取整函数会带来较大误差的问题。所提改进策略的具体调制方法为：当计算出需要上桥臂切除1个子模块、下桥臂投入1个子模块时，在下桥臂投入子模块的同时保持上桥臂中子模块状态不变，这样在原有的两个电平之间就多出一个过渡状态。变换器工作在过渡状态时的输出电平介于原有的两个输出电平之间。由此，对子模块为N的MMC，在原来的N+1个输出电平之间均会增加1个过渡电平，变换器的输出电平即由原来的N+1提升至2N+1个，表2所示的5个电平数就增加为表3所示的9个电平，增加部分表示采用改进调制策略时增加的过渡电平。

本文所提改进调制算法实现方法简单，在不需要增加额外的硬件设施的前提下即可将变换器的输出电平数提高近一倍，减小阶梯波相邻电平之间的电压差，增大阶梯波对正弦波的逼近程度，显著改善变换器的输出电压波形，提高变换器的输出性能。

表3 包含4个子模块的MMC改进工作状态表Tab.3 Improved work status table of MMC with 4 sub-modules

3 改进调制策略仿真结果与分析

为验证本文所提改进调制策略的有效性，在PSCAD/EMTDC电磁暂态软件仿真平台上搭建了图所示MMC变换器的详细仿真模型，为验证本文所提调制策略的优越性，对传统最近电压逼近调制和本文所提的改进策略进行了对比仿真，仿真参数如下：桥臂子模块数N=4，直流母线电压Udc=9 kV，子模块电容C=5 000μF，电容电压参考值Ucref=2.25 kV，仿真结果如图5～图7所示。

图5 交流侧输出电压波形Fig.5 Waveforms of output voltages on AC side

图5（a）和图5（b）分别为采用传统NLM调制策略和改进型NLM调制策略时MMC变换器交流侧输出电压波形，由仿真结果可以看出，采用改进型调制策略后，变换器交流侧输出电压波形由5个电平增加到9个电平，电平数提高了近一倍，从而有效减小了阶梯波与正弦调制波之间的误差，调制策略的逼近效果得到明显改善。

图6（a）和图6（b）分别为采用传统NLM调制和所提改进调制策略时，变换器输出电压的FFT分析结果。

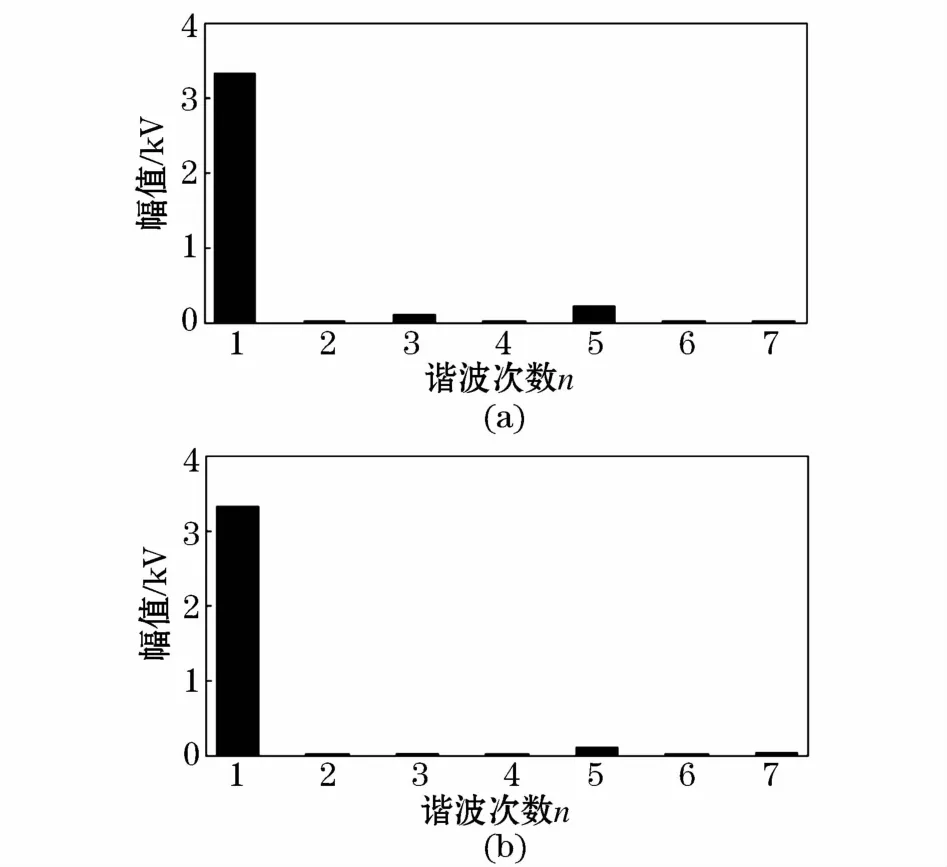
图6 交流侧输出电压FFT分析结果Fig.6 FFT results of output voltages on AC side

对比图6（a）、图6（b）波形可知，采用改进型调制策略后，由于变换器交流侧输出电压电平数增加，变换器输出电压谐波含量明显减小；采用改进调制策略后，输出电压中的3、5次谐波含量相较于传统NLM调制明显减小，变换器的输出性能得到显著提升。

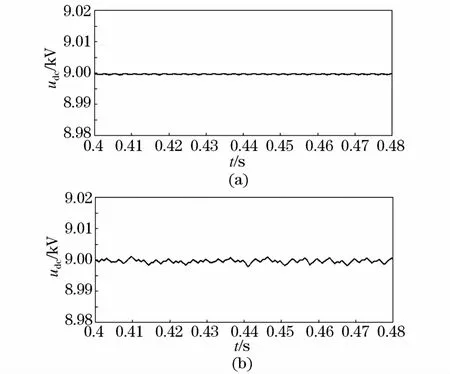
图7 直流母线电压波形Fig.7 Waveforms of DC bus voltage

图7（a）和图7（b）分别为采用两种调制策略时的变换器直流母线电压。对于改进型调制策略，由于每个相单元投入的子模块总数Nin不再固定，造成直流母线电压波动幅值较采用传统最近电平逼近调制算法时增大，不过该波动幅值仍在可以接受的较小范围以内，其基本不影响 MMC变换器的正常工作。

图8（a）、图8（b）分别为采用两种调制策略时a相单元上桥臂中4个子模块的电容电压波形。由图可见，两种调制策略下的子模块电容电压均维持稳定且所有子模块电容电压保持均衡。对比图8中的波形可知，采用改进型调制策略时，子模块电容电压的平均值较采用传统调制策略时略低，这是由于改进型调制策略增加的过渡状态增加了每相单元投入的子模块数目。原来固有的每个工作状态仅有4个子模块投入运行，而新增加的过渡状态则有5个子模块投入到桥臂中，在稳态连续运行过程中，可将相单元整体投入的子模块数等效平均为4.5个，因此子模块电容电压的平均值下降到2 kV左右。由于等效的投入子模块数增多，子模块电容电压波动幅值也相应地减小，更小的电容电压波动幅值有利于延长电容器的使用寿命，这也进一步体现了所提改进控制策略的优势。

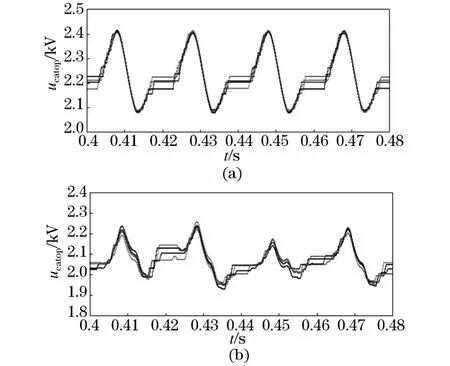
图8 子模块电容电压波形Fig.8 Waveforms of sub-module capacitor voltage

4 结束语

针对MMC包含子模块数较少时最近电平调制策略的取整函数会带来较大误差的问题，本文提出了一种改进调制策略，所提策略实现方法简单，并可以将变换器的输出电平数由N+1提高至2N+1。通过提高输出电平数，所提策略能够大大改善阶梯波对正弦调制波的逼近效果，有效降低变换器输出电压中的谐波含量，并能在一定程度上减小子模块电容压波动幅值，降低电容器的损耗，延长电容器的使用寿命。