基于有限元方法的变压器铁芯优化仿真*
2017-12-21刘旭光顾小虎于春雷张晓同刘斌杨庆福
刘旭光,顾小虎,于春雷,张晓同,刘斌,杨庆福
(1.南瑞集团公司<国网电力科学研究院>,南京 211100;2.江苏南瑞帕威尔电气有限公司,南京 211100;3.南昌航空大学,南昌 330000)
0 引 言
随着城市与农村电网建设的快速发展,变压器的需求量呈快速增长的趋势,它是否节能十分重要[1]。变压器自身的能量消耗有两种:一种是铁芯产生的空载损耗,另一种是主要由导线产生的负载损耗[2]。虽然空载损耗比额定负载损耗小很多,但只要产品挂网运行,不管负载大小,空载损耗总是存在的,尤其在变压器轻载情况下,空载损耗占总损耗的比重很大。因此,降低空载损耗是变压器技术发展的一个趋势。
变压器铁芯柱截面的大小直接关乎铜材的使用量,在保持其他参数不变的情况下,心柱截面积增大,磁通密度降低,损耗减少,但其截面积增大,铜材的使用量增多。若以增大原材料的使用量为代价来减少空载损耗则得不偿失。文献[3]和文献[4]对降低空载损耗的方法进行了简要的阐述,通常都是从硅钢材料的升级、工艺的改进等方面进行分析,并未提出铁芯结构上的改进方法。针对上述问题,采取一些可行方法达到降低空载损耗的目的,本文提出增大铁轭截面积以降低空载损耗的方法,并通过四维可视化算法进行理论分析和有限元分析软件仿真验证,在保证成本可控的情况下,达到降低损耗目的。
1 空载损耗理论分析研究
空载损耗主要包括磁滞损耗、涡流损耗。通常空载损耗数值为变压器铁芯重量、铁芯材料的单位损耗、铁芯加工工艺系数三者的乘积,而其铁芯材料的单位损耗由磁通密度的大小确定,可见空载损耗与铁芯重量、磁通密度有关。
变压器铁芯损耗的计算已经提出一些有效模拟方法,诸如均匀化处理等方法,但是铁芯在垂直进入的漏磁通作用下所产生的损耗与通常损耗不同,称之为附加损耗。对于大型变压器多级铁芯的“末级铁”内部由于变压器线圈漏磁通进入,将产生可观的涡流损耗[5]。当外施交变磁场垂直进入取向硅钢叠片组时,面临磁通进入的若干张硅钢片中可能感应出很强涡流,由此产生的涡流损耗在总铁损中可能占据一定比重。实际中硅钢片中除了垂直进入的漏磁通外,还通过与硅钢片平行的交变磁通,产生的涡流为三维,其仅限于单片内部流动。在正弦磁通情况时,频率范围内空载损耗表达式为:
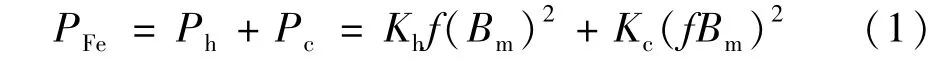
式中的Ph、Pc为磁滞损耗、涡流损耗;Kh、Kc为磁滞铁芯单位损耗、涡流铁芯单位损耗;f为工作频率;Bm为交流磁通分量幅值。
有限元分析软件常采用上式表达式进行空载损耗计算,其中Kh、Kc均由铁芯材料制造厂商提供的损耗曲线得出。
2 变压器数学模型及优化分析
铁芯直径的大小直接影响有效材料的消耗、变压器体积及性能参数等技术经济指标,因此选择技术经济合理的铁芯是变压器计算的重要内容[6],合理的铁芯直径使得硅钢片和导线用量的比例适当,达到最经济效果。
根据电磁感应原理,绕组中的感应电势为:
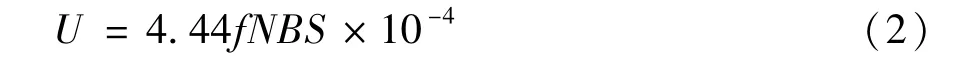
式中f、N、B、S分别表示为电网频率、绕组匝数、磁通密度、铁芯截面积。我国电网频率为50 Hz,故感应电动势数值与三个变量N、B、S表达,利用MATLAB软件编程可得其可视化变化趋势图,如图1所示。
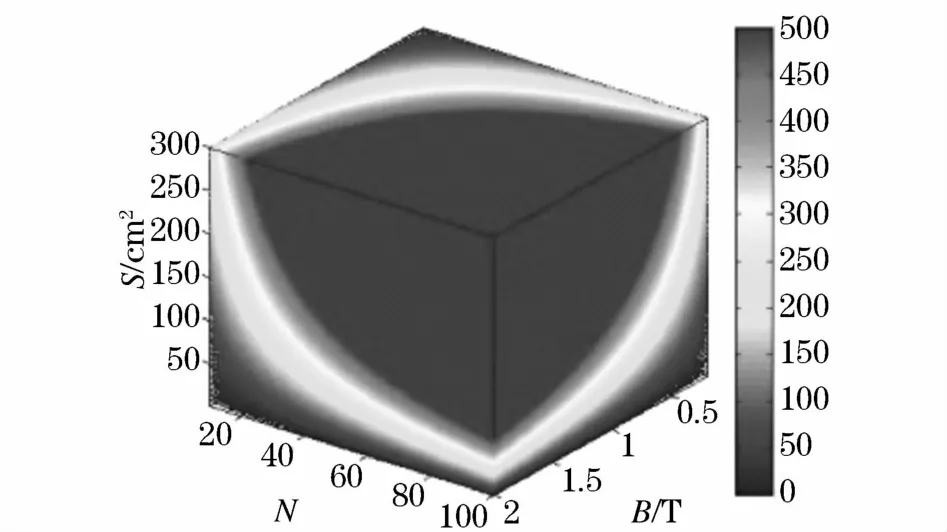
图1 感应电动势可视化图Fig.1 Visualization diagram of induced electromotive force
图1中三个变量N、B、S的取值范围依次为(10,100)、(0.2,2)T、(1,300)cm2,由上图可知三个变量的变化对感应电动势呈非线性变化趋势。图1感应电动势变化范围为(0,500)V,浅色代表数值较小,深色代表数值较大;当变量增大时其可视化图颜色加深,即感应电动势增大。
本文设计的模型低压侧电压为0.4 kV,故从图1中求取满足U=0.4 kV条件的解域,如图2所示,图中绿色区域(深色)即为函数U的解域集。
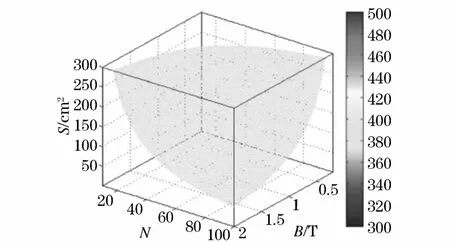
图2 U=0.4 kV解集可视化图Fig.2 Visualization diagram when U=0.4 kV solution set
由图2可知,当感应电动势一定时,B选取大,N不变时,则S较小,硅钢用量较少;B选取小,N不变时,则S较大,硅钢用量较大。
当变压器空载损耗超出标准范围较小时,传统采用同时改变铁芯芯柱、轭截面积方式降低空载损耗,易造成变压器线圈材料增加。
以某公司S13-M-400变压器产品为例,产品铁轭截面积未加大前,其变压器铁芯损耗理论值为419 W,该数值超过设计标准值,未符合标准,故需找到一种合适方法解决该问题。通过几组数据进行曲线拟合可知,当增大铁轭截面积,铁芯柱截面积不变,空载损耗随铁芯总重变化的趋势如图3所示。
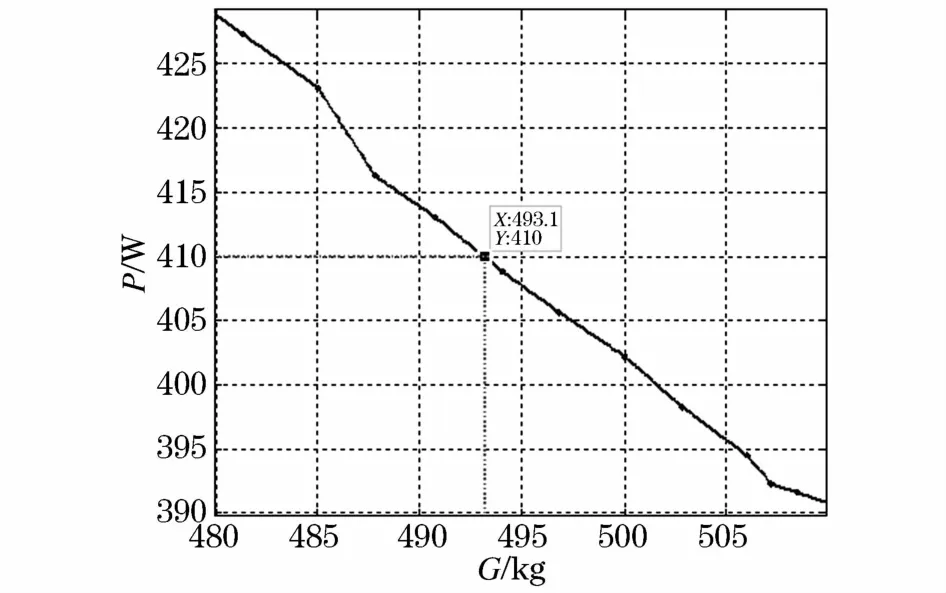
图3 空载损耗随铁芯重量变化图Fig.3 Diagram of no-load loss change with the weight of the iron core
图3中坐标点为空载损耗临界点,即GB 1094中规定额定空载损耗410 W时,铁芯总重对应为493.1 kg。当铁轭截面积增大,相应的磁通密度降低,尽管铁芯总重增大,但空载损耗下降明显。空载损耗与磁通密度影响紧密,如若同时降低芯柱磁通密度,线圈成本就会增加,由上图可知当铁轭截面积的增大,成本增加幅度较小。
可见,铁轭截面积增加对空载损耗的降低作用明显,且可有效控制高性能变压器材料成本。
3 变压器模型计算
变压器空载损耗计算是变压器设计中一个较困难问题,目前设计工程师常利用铁芯平均磁通密度方法进行空载损耗计算,虽然其可满足工程需求,但铁芯磁通密度分布无法进行精确测量,对于产品的性能优化有一定局限性[7],故需利用有限元方法进行计算验证。
本文利用有限元分析软件在瞬态场进行变压器铁轭加大前后模型的仿真计算。求解三维瞬态磁场时,其棱边上的矢量位自由度采用了一阶元计算,而节点上的标量位自由度采用二阶元计算[8]。
电磁分析实际是求解给定边界条件下的麦克斯韦尔方程组问题,是电磁场数值计算和应用研究的基础[9]。三维瞬态场采用T-Ω算法,利用局部剖分法计算三维瞬态所带来的效应,对于低频瞬态磁场,麦克斯韦方程组表达式为:
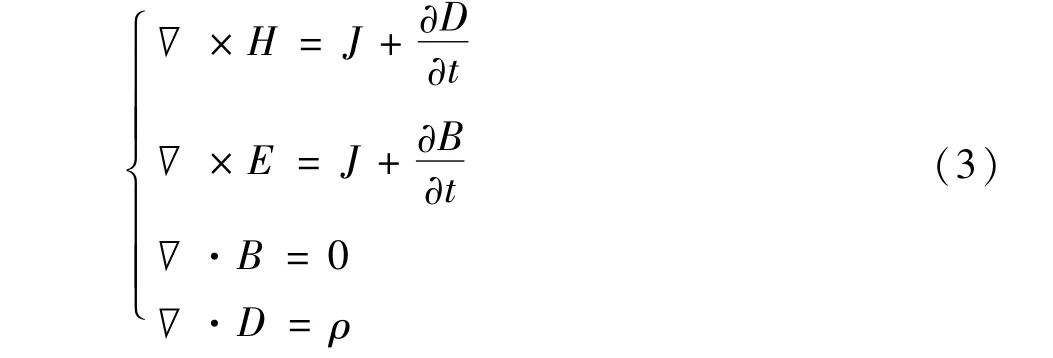
式中E、H、D、B、J、ρ分别为电场强度、磁场强度、电通量密度、磁通量密度、电流密度和电荷密度。对上式方程组中的第一个方程进行取散度,利用第四个方程结果可得:

式中ε、μ、σ分别表示媒质介电常数、磁导率和电导率。由于变压器没有自由电荷,电荷密度可忽略,即式(4)为0。
依据上述理论分析,针对铁轭截面积增加进行优化设计,变压器空载损耗优化设计前后基本参数如表1所示,模型材料属性如表2所示。
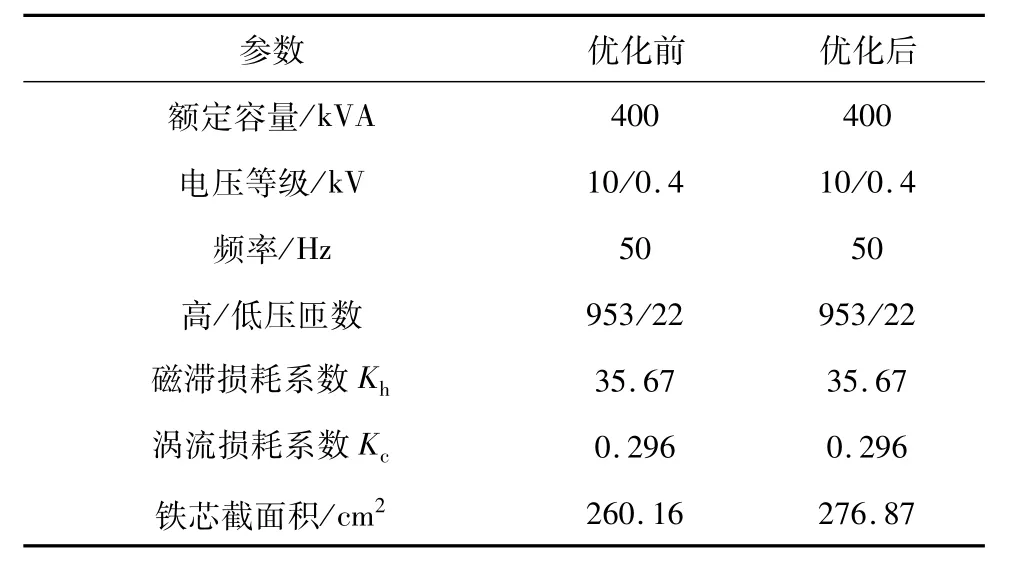
表1 性能参数Tab.1 Performance parameters
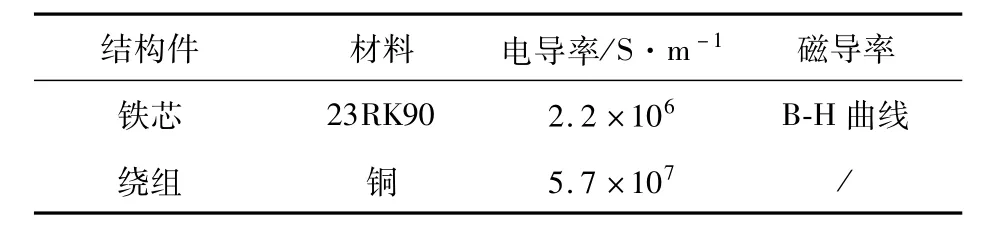
表2 材料属性Tab.2 Material properties
铁轭截面积增加范围由铁芯牌号、铁芯结构尺寸、制造工艺等因素决定[10-11],本文模型铁轭横截面积增加约6.47%左右。变压器铁芯主级片宽为140 mm,仿真环境设置除铁轭面积不同,其余参数均一致,本文针对优化前后两种模型进行仿真验证。
4 空载损耗优化仿真
对于结构简单模型来说,常采用有限元分析软件进行二维模型建模分析,但鉴于其变压器铁芯为叠片形式,结构相对复杂;为提高仿真计算精度,故应采取三维模型进行仿真分析。
由于笔者主要研究变压器磁场分布及空载损耗分析,为节省仿真计算时间及提高效率,笔者将变压器简化模型进行1/2求解计算。由于本文仅研究铁轭加大对空载损耗,故该变压器模型其余结构件可忽略,其中激励源采用电压源,不考虑谐波影响。
利用有限元软件在瞬态场进行分析计算,优化前后模型时刻铁轭加大前后磁通密度变化及分布,其结果如图4所示。
由图4可知,铁轭横截面积未加大前,该变压器铁轭磁通密度颜色较深,即其铁轭磁通密度较大;铁轭横截面积增加后其颜色较浅,即其铁轭磁通密度较小。在变压器模型中取铁轭上某点进行仿真计算,查看该点磁通密度变化情况,如图5所示。
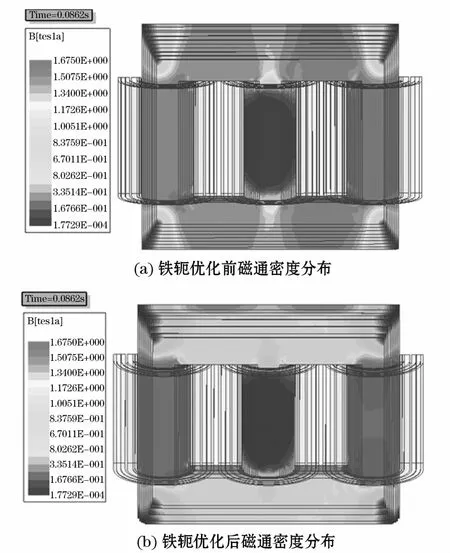
图4 t=0.086 2 s时刻铁芯磁通密度分布Fig.4 Distribution of magnetic flux density when t=0.086 2 s
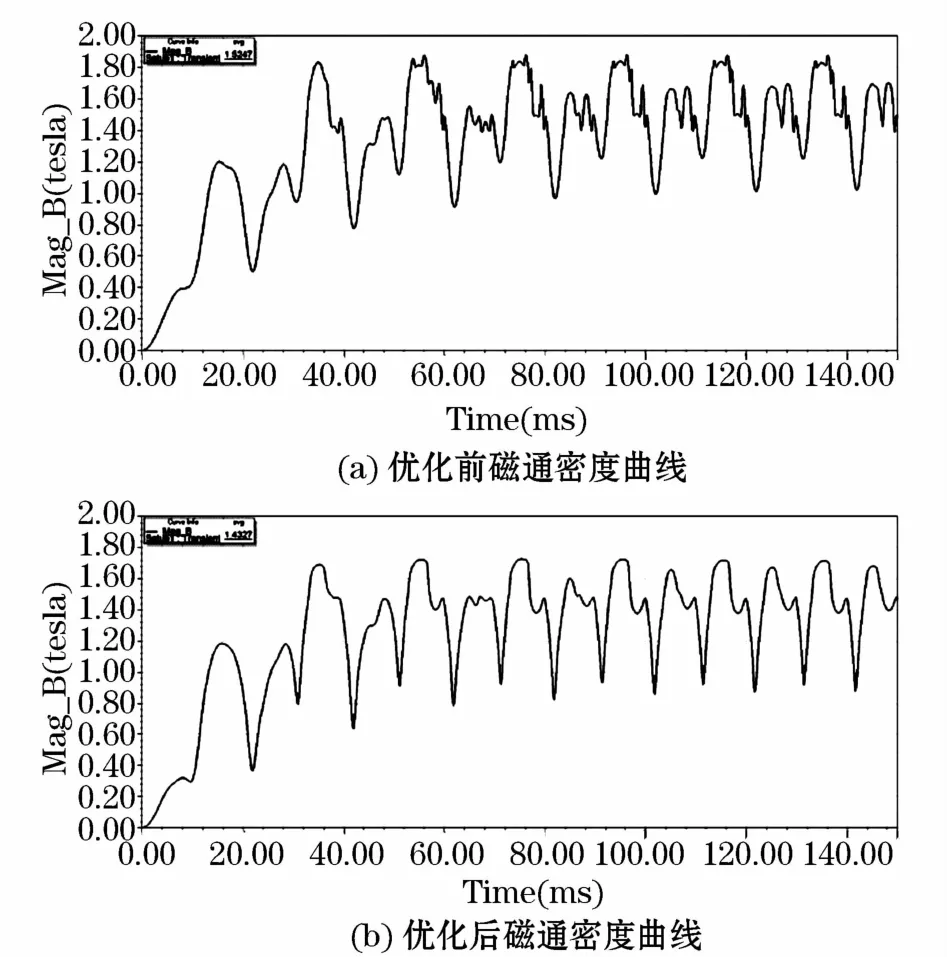
图5 铁芯磁通密度分布Fig.5 Distribution of magnetic flux density
图5(a)为铁轭优化前某点磁通密度变化,其铁轭平均磁通密度为1.524 7 T,图5(b)为铁轭优化后某点磁通密度变化,其铁轭平均磁通密度为1.432 7 T。依据磁通量不变原理,由于优化铁轭横截面积增大,激励源不变,故其磁通密度降低,上述仿真磁通密度结果也验证符合理论计算。变压器模型优化前后空载损耗仿真计算,如图6所示。
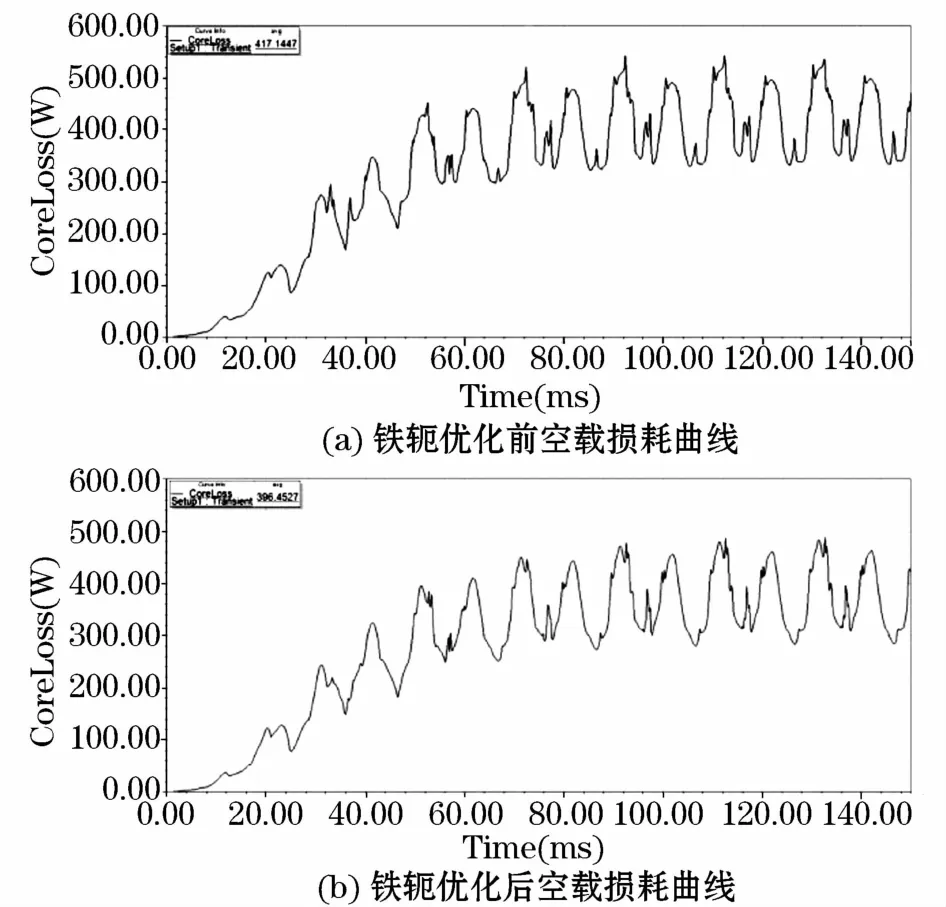
图6 空载损耗曲线Fig.6 No-load loss curve
图6为铁轭优化前后空载损耗曲线,优化前其变压器模型空载损耗仿真数值为417.144 7 W,质量为481.29 kg;改善后其数值为396.452 7 W,质量为494.45 kg;优化前后空载损耗数值下降约4.95%,质量增加2.78%,成本增加相比性能降低较优,验证了设计可行性。
5 结束语
本文主要针对铁轭截面积加大对变压器磁场及损耗变化的影响进行了理论分析,利用有限元分析软件仿真验证其可行性。采用铁轭加大方式可使得空载损耗降低,对于企业今后产品技术研究有推动作用。
