完备二元序列的相关函数

崇金凤，卓泽朋，王春侠

（淮北师范大学 数学科学学院，安徽 淮北 235000）

完备二元序列的相关函数

崇金凤，卓泽朋，王春侠

（淮北师范大学 数学科学学院，安徽 淮北 235000）

文章在研究两个相同周期的完备二元序列互相关函数关系的基础上，给出了4个相同周期的完备二元序列互相关函数间关系，并分析完备二元序列的互相关函数和自相关函数之间的关系.

二元序列；完备序列；互相关函数；自相关函数

0 引言

二元序列在多址通信中可用作地址信号，在连续波雷达中可用作测距信号，在数字通信中可用作群同步信号，还在保密通信中起加密作用等.二元序列是很多序列的构造的基础，关于它的自相关和互相关函数的研究一直是很多学者研讨的热点［1-4］，这些成果在扩频通信和密码学中都有重要的应用.本文给出了4个相同周期序列的互相关函数关系，它可以为研究完备二元序列的互相关函数和自相关函数间的关系提供重要参考.

1 预备知识

令a={ai},ai∈F2（含0和1的有限域）为1个二元序列，若存在正整数l，使得对所有的i，有ai=ai+l，则称序列a是周期序列，把满足此式的最小正整数叫做序列a的周期.

定义1［5］设a={ai}和b={bi}都是周期为N的二元序列，则它们的互相关函数定义为：

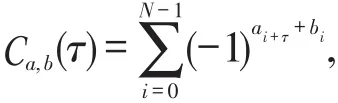
这里0≤τ≤N-1，下标模N运算.特别地，当a=b时，称Ca,a(τ)为序列a的自相关函数，并另记为Aa(τ).

定义2［5］周期为N的二元序列a称为是二值的，如果它的自相关函数Aa(τ)满足：

这里K是常数.当K=-1且N是奇数或K=0且N是偶数时，称序列a具有理想二值自相关函数，此时序列a称为是完备二元序列.为了讨论方便起见，令

PSo={a是周期为N的二元序列|Aa(τ)=-1,τ≢0(modN)且N是奇数}，

PSe={a是周期为N的二元序列|Aa(τ)=0,τ≢0(modN)且N是偶数}.

具有理想二值自相关函数的二元序列在通信中有诸多应用，如雷达测距，硬件测试，编码和密码学等，周期为2n-1的具有理想二值自相关函数的二元序列对应于(2n-1,2n-1-1,2n-2-1)的循环哈达玛差分集.周期为N二元序列a称为是平衡的，如果当N是偶数时，每个周期中1和0的个数都是N/2；或当N是奇数时，每个周期中1和0的个数是(N±1)/2.平衡的二元序列在通信和密码学中也有着广泛应用.

注11）根据（1）式，有

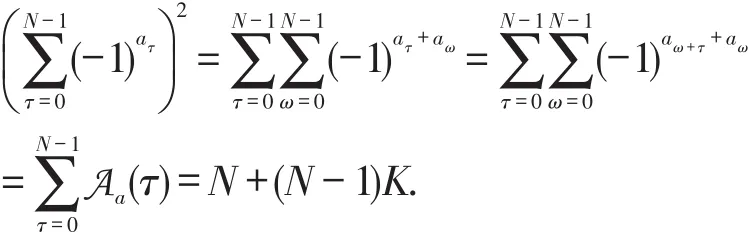
所以，当a∈PSo时，

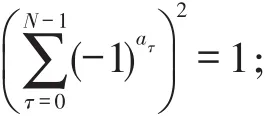
或

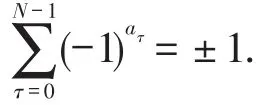
当a∈PSe时，

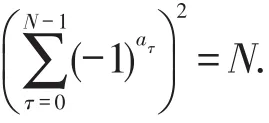
2

）当a,b∈PSo时，

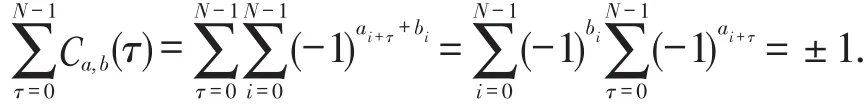
2 主要结果

在本节中，首先研究任意4个同周期的二元序列，它们在互相关函数间的关系，利用此等式，可以方便研究完备二元序列的互相关函数和自相关函数间的关系.

定理1设a,b,x和y是4个周期为N的二元序列，则

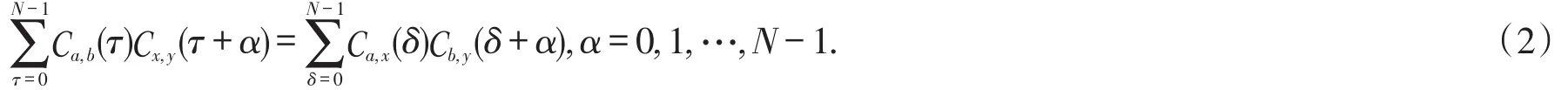
证明为方便起见，记（2）式的左端为L，根据互相关函数的定义，有

证毕.

在定理1中，特别地当a=x,b=y时，有

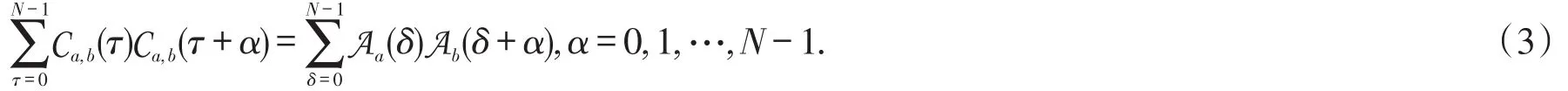
注2（a） 在（3）式中，当a,b∈PSo时，利用（1）式得

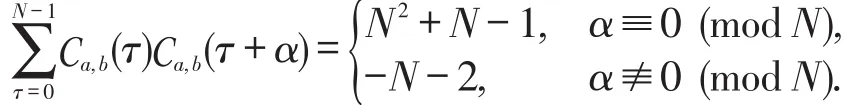
（b）在（3）式中，如果α=0，那么

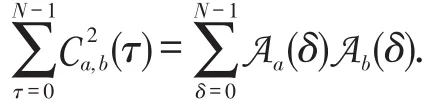
由于Aa(0)=Ab(0)=N，所以，

（c）根据定义2，当Aa(τ)和Ab(τ)是二值时，有

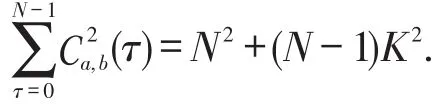
因此，当a,b∈PSo时，

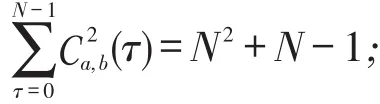
当a,b∈PSe时，

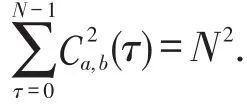
（d）对等式（4）利用柯西不等式得，

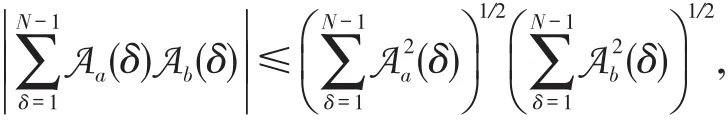
或

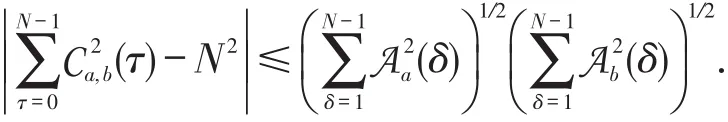
所以，

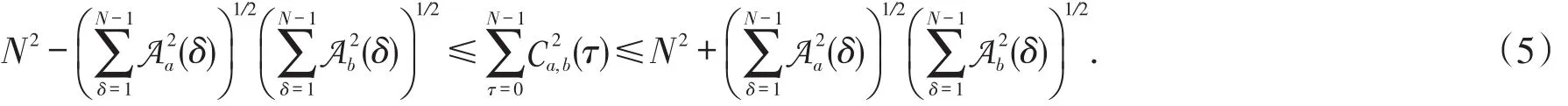
不等式（5）给出了序列的互相关函数与自相关函数间的一种不等关系.对于扩频多址系统，人们希望所使用序列的|Ca,b(τ)|尽可能的小，而不等式（5）表明，此时序列的|Aa(τ)|和|Ab(τ)|也应该尽可能的小.

注3在式（2）中，当b=y时，有

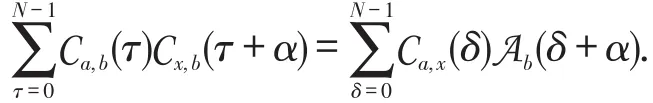
进一步地，如果α=0，那么

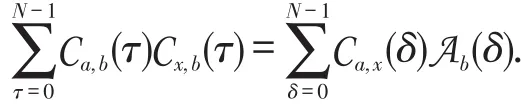
在这里，当b∈PSe时，

在（6）式中，当a=x时，有

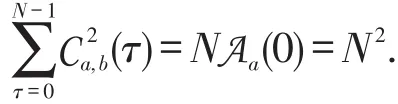
3 结论

本文给出了4个相同周期的完备二元序列互相关函数间关系的定理，并深入分析完备二元序列的互相关函数和自相关函数间的关系.本文的结果进一步丰富了序列的互相关函数性质，为以后的研究工作提供了一定的帮助和借鉴.

［1］NO J S，GOLOMB S W，GONG G，et al.Binary pseudo-random sequences of period2n-1with ideal autocorrelation［J］.IEEE Transactions on Information Theory，1998，44（2）：814-817.

［2］卓泽朋，肖国镇.完备二元序列的互相关性［J］.北京邮电大学学报，2010，33（2）：78-81.

［3］FAN J M，XU Y G，XIA Y B，et al.Two families of Niho sequences having four-valued cross correlation withm-sequenc⁃es［J］.Science China Mathematics，2017，60.［207-04-21］.https://doi.org/10.1007/s11425-016-9061-y.doi：10.1007/s11425-016-9061-y.

［4］ZHANG T，LI S X，FENG T，et al.Some new results on the cross correlation ofm-sequences［J］.IEEE Transactions on Information Theory，2014，60（5）：3062-3068.

［5］GOLOMB S W，GONG G.Signal designs with good correlation：for wireless communications，cryptography and radar appli⁃cations［M］.New York：Cambridge University Press，2005.

Correlation Functions of Perfect Binary Sequences

CHONG Jinfeng，ZHUO Zepeng，WANG Chunxia
（School of Mathematical Sciences，Huaibei Normal University，235000，Huaibei，Anhui，China）

Based on the research of two of the same period perfect binary sequences，on the basis of crosscorrelation function relations，the theorem for four of the same period perfect binary sequences cross-correla⁃tion function relations is given，and in-depth analysis of the perfect binary sequence of cross-correlation function and the relationship between the autocorrelation function.

binary sequence；perfect sequence；cross-correlation function；autocorrelation function

TN 918.1

A

2095-0691（2017）04-0016-04

2017-05-31

安徽省自然科学基金项目(1608085MF143);安徽高校优秀青年人才支持计划重点项目(gxyqZD2016112)

崇金凤（1979- ），女，安徽天长人，硕士，副教授，研究方向为密码学及信息安全.