一种求解约束非线性方程组的非精确Levenberg-Marquardt算法

赵 琪，芮绍平

（淮北师范大学 数学科学学院，安徽 淮北 235000）

一种求解约束非线性方程组的非精确Levenberg-Marquardt算法

赵 琪，芮绍平

（淮北师范大学 数学科学学院，安徽 淮北 235000）

利用绝对值函数的光滑函数将约束非线性方程组转化为一个光滑方程组，用非精确Levenberg-Mar⁃quardt方法求解该光滑方程组，得到一种求解约束非线性方程组的非精确Levenberg-Marquardt算法，证明该算法具有全局收敛性，并给出数值实验.

约束非线性方程；非精确Levenberg-Marquardt算法；全局收敛性

0 引言

设F:Rn→Rn是连续可微映射，约束非线性方程组问题一般形式如下：

其中h:Rn→Rm是一个连续可微映射，且h(x)=(h1(x),h2(x),…,hm(x))T.本文中，假设问题（1）的解集非空，表示欧几里得范数，R++和R+分别表示集合{x∈R|x＞0} 和{x∈R|x≥0}.

约束非线性方程组问题（1）出现在各种数学模型中，如工程设计中的非线性互补、变分不等式问题，经济学中的最优潮流（OPF）问题和可用传输能力（ATC）问题等［1-3］.求解问题（1）的典型方法是基于最优化方法，即寻找下面最优化问题的全局最优解：

一般情况下，与基于最优化方法相比，求解方程组更简单且计算量少.此外，基于最优化方法的解是问题（2）的稳定点，但不一定是问题（1）的解.所以，本文将考虑通过使用绝对值松弛变量函数把约束方程组转化为如下半光滑方程组：

L-M方法是由Levenberg［4］提出，并由Marquardt［5］做进一步研究，此方法克服Jacobian矩阵几乎奇异或坏条件时带来的困难.本文所提出的是一个Armijo步长下的非精确Levenberg-Marquardt算法，此算法具有全局收敛性质.

1 光滑函数和相关性质

定义1［6］（光滑逼近函数） 给定函数H:Rn→Rn，称光滑函数Hˉ(μ,x):Rn+1→Rn(μ＞0)是H的光滑逼近函数，如果对任意的(μ,x)∈R++×Rn，存在κ＞0，使得：

这里κ不依赖于x，则称Hˉ是H的一致光滑逼近函数.

对绝对值函数qi(ti):=||

ti，i=1,2,…,m，采用如下光滑函数［7］：

于是得到绝对值函数q(t):=||t的光滑函数：

事实上，由

可以得到

即当m→+∞时，qˉ(μ,t)光滑逼近绝对值函数

令z=(μ,x,t)∈R++×Rn×Rm，定义映射H：

于是求解方程（3）可转化为求解光滑方程组（7）.下面首先研究光滑函数H(z)的性质.

定理1映射H是连续可微的，对 ∀z=(μ,x,t)∈R++×Rn×Rm，记H(z)的Jacobian矩阵为H′(z)，则有：

其中 ∇F(x)，∇h(x)分别是F(x)，h(x)的Jacobian矩阵，

2 非精确Levenberg-Marquardt算法

本节给出一个求解约束非线性方程组的非精确L-M算法.为此，首先令其中，

由（6）式可知：

通过函数H(z)可以定义一个价值函数ψ(z):Rn+m+1→R+如下：

显然ψ(·)在任意点z=(μ,w)∈R++×Rn×Rm处连续可微.

取γ∈(0,1)，μˉ＞0 ，使得γμˉ＜1，令

这里{αk}⊂R++.由上式可知，{βk} 是单调递减的序列，且因为β0＜γ＜1，故对任意的z0∈R++×Rn×Rm均有

算法（非精确L-M算法）

步骤0选取参数α,ρ,β,η∈(0,1)，δ∈(0,2]. 选取参数γ∈(0,1)满足ˉ＜1. 选取初始点z0=(μ0,w0)

步骤1若zk满足终止条件，则停止；否则，计算且由（10）式、（11）式计算βk.并进入第2步.

步骤2令 (dk)μ=-μk+βkˉ，并求解方程

得 (dk)w，其中

步骤3若下式成立

则令zk+1=zk+dk，转到第5步；否则，转到第4步.

步骤4令dk=-αk∇ψ(zk)+βk，其中0)∈R1+n+m. 记mk为满足下式的最小负整数m：

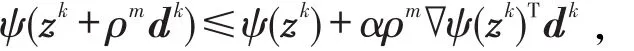
步骤5令转到第1步.

在算法第2步中，想要非精确地求解方程（12），即(dk)w满足：

其中rk是残差向量和非精确地求解方程（12）的措施.由上式可知：

3 收敛性分析

现讨论算法的全局收敛性.为方便起见，引入如下几个指标集：

L={k∈N|算法第2步、第4步在zk-1处被接受 }和K={k|K1⋃K2} ，

这里

假设1由算法产生的序列{zk}满足

假设2残差向量满足：

其中η∈(0,1)，vk=ο(dist(zk,z∗)).

定理2假设对任意整数k≥0，μk∈R++，有μk≥βk，那么算法可产生一个无穷序列{zk}，且满足：μk∈R++，μk≥βk.

证明由于β0≤γ＜1 ，所以z0=(μ0,w0)满足当算法取第 2 步时，由和当算法取第4步时，由

可知

由数学归纳法可知，迭代下去算法可产生一个无穷序列{zk} 满足

定理3设{zk}是算法产生的无穷序列，z∗是{zk}的任一聚点，{zk}K是对应的收敛子序列.那么z∗是ψ(z)的稳定点.

证明由于η∈(0,1)，显然是单调下降的序列.若K1为无限集，则所以{zk}的任一聚点都是ψ(z)的稳定点，即z∗是ψ(z)的稳定点.若K1为有限集，假设z∗不是ψ(z)的稳定点. 下面分两种情况：（i）K2为无限集；（ii）K2为有限集.

当K2为无限集时，对任一k∈K2，有：

且当任意k∈K2时，有：

当K2为有限集时，不失一般性，设对任意k∈K，dk=((dk)μ,(dk)w)，其中(dk)μ=-μk+ˉ，(dk)w是（12）式的近似解，其残差向量：

又

假设

对任一k∈K3，有：，则存在子集K3⊆K，使得：

因为{zk}

K→z∗(k→∞,k∈K)，序列是有界的，所以由上式和（17）式，可得：

又由假设2知由（18）式知：

考虑到{zk}K收敛于ψ(zk)的非稳定点z∗，所以由（19）式可知：

这与假设1矛盾，因此假设不成立，故

这样由（14）、（15）、（16）和（20）式可知

4 数值实验

为了测试算法性能，本节进行数值实验.算法中的参数取值如下：

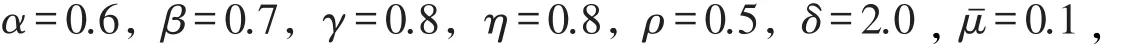
实验终止准则设为‖H(zk)‖≤10-6.试验结果见表1.

算例1试验方程为：

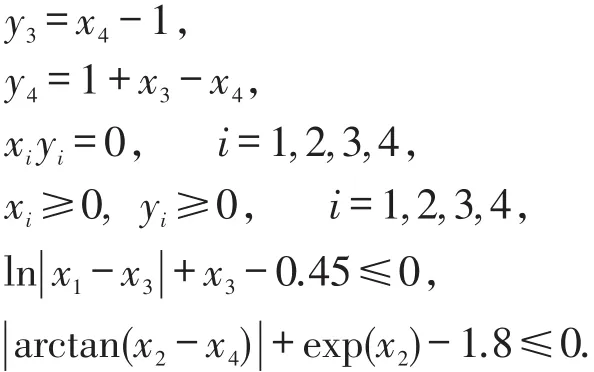
算例2试验方程为：

表1 数值实验结果

从表1结果可以看出，本文所设计的算法稳定可靠，所需迭代次数和计算时间较少，说明文中设计的算法适合约束非线性方程的求解.

［1］YANG Liu，CHEN Yanping，TONG Xiaojiao.Smoothing Newton-like method for the solution of nonlinear systems of equali⁃ties and inequalities［J］.Numerical Mathematics（Theory，Methods and Applications），2009，2（2）：224-236.

［2］BELLAVIA S，MACCONI M，MORINI B.An affine dcaling trust-region approach to bounded-constrained nonlinear sys⁃tems［J］.Applied Numerical Mathematics，2003，44（3）：257-280.

［3］FISCHER A.Solution of monotone complementarity problems with locally Lipschitzian functions［J］.Mathematical Program⁃ming，1997，76（3）：513-532.

［4］LEVENBERG K.A method for the solution of certain nonlinear problems in least squares［J］.Quarterly Applied Mathemat⁃ics，1944，2（2）：164-166.

［5］MARQUARDT D W.An algorithm for least-squares estimation of nonlinear inequalities［J］.SIAM Journal on Applied Mathematics，1963，11（2）：431-441.

［6］韩继业，修乃华，戚厚铎.非线性互补理论与算法［M］.上海：上海科学技术出版社，2006.

［7］QI Liqun，SUN Defeng.Smoothing functions and a smoothing Newton method for complementarity and variational inequali⁃ty problems［J］.Journal of Optimization Theory and Applications，2002，113（1）：121-147.

An Inexact Levenberg-Marquardt Method for Solving Constrained Nonlinear Equations

ZHAO Qi，RUI Shaoping
（School of Mathematical Sciences，Huaibei Normal University，235000，Huaibei，Anhui，China）

In this paper，we first transform the constrained nonlinear equations to a system of smooth equa⁃tions by using the smoothing approximation function of absolute value function.Then an inexact Levenberg-Marquardt method is used to solve the system of smooth equations，and get an inexact Levenberg-Marquardt algorithm to solve constrained nonlinear equations，and the global convergence is obtained.Preliminary nu⁃merical results are given.

constrained nonlinear equations；inexact Levenberg-Marquardt method；global convergence

O 221.2

A

2095-0691（2017）04-0001-06

2017-05-31

安徽省自然科学基金项目（1508085SMA204）；高校优秀青年人才支持计划重点项目（gxyqZD2016109）

赵 琪（1992- ），女，安徽淮北人，硕士生，从事最优化研究.通信作者：芮绍平（1978- ），男，安徽安庆人，博士，副教授，研究方向：优化理论与计算、金融优化.