带有非单调功能性反应的时滞捕食者-食饵系统的多个周期正解

孔德玉，梁 峰，王 皓

（安徽师范大学 数学计算机科学学院，安徽 芜湖 241002）

带有非单调功能性反应的时滞捕食者-食饵系统的多个周期正解

孔德玉，梁 峰，王 皓

（安徽师范大学 数学计算机科学学院，安徽 芜湖 241002）

文章研究带有非单调功能性反应的时滞捕食者-食饵系统中多个周期正解的存在性.通过使用Mawhin′s重合度拓展定理，得到一些新的结果，推广现存文献的主要结果.不同的是主要结果是参数相关的.最后，给出结果的一个应用.

周期正解；捕食者-食饵系统；Fredholm算子；Mawhin′s重合度延拓定理

0 引言

Lotka-Voterra系统的几种模型、稳定性和周期现象等在文献［1］中有一定的介绍.近些年，拓扑度［2］也开始被广泛应用于Lotka-Voterra系统的周期解存在性研究［3-9］中，并取得很多可喜的结果，使得Lotka-Voterra系统的研究更为丰富.其中，Wang等［10］研究如下捕食者-食饵系统

其中x(t),y(t),z(t)分别表示食饵、捕食者-1和捕食者-2的密度，a(t),b(t),e(t),f(t),d1(t),d2(t),τ1(t),τ2(t),g1(t),g2(t)全是正ω-周期连续函数，m＞0，n＞0是两个实常数，K(s):ℝ+→ℝ+是一个使可测的规范化函数.毫无疑问，两个捕食者是竞争关系.通过使用Mawhin′s重合度拓展定理，文献［10］得到系统（1.1）至少有4个ω-周期正解.

本文将对系统（1.1）引入一个参数，从而推广文献［10］的主要结果，使之在生物学中具有更广泛的研究意义.因此，我们考虑如下带有非单调功能性反应的时滞捕食者-食饵系统其中γ≥1且为一个参数.易看出，当γ=1，系统(1.2)便可退化成系统(1.1).所以，可看出本文研究包含文献[10]的研究成果，并考虑出参数γ可取范围.从而得出更好的研究结果.

为了简便，全文将采用以下记号：

其中f(t)是一个ω-周期恒正连续的函数，

通过简单计算可得

1 准备工作

本文的主要工作是研究系统（1.2）周期正解的存在性，为此，我们先引入拓扑度的一些有关概念和重要结果.

定义1设X和Y是Banach空间，L:D(L)⊂X→Y是一个线性映射，如果：

（i）ImL是Y的闭子空间，

（ii）dimkerL=codimImL＜∞，

则L是一个指标为零的Fredholm算子.

若L是一个指标为零的Fredholm算子，令X1=kerL，Y2=ImL，则存在直和X=X1⊕X2，Y=Y1⊕Y2，那么存在连续映射

从而可知L|kerP⋂D(L):(I-P)X→ImL是可逆的，且记它的逆为Kp.

定义2设X和Y是Banach空间，Ω⊂X是一个有界开集，L:D(L)⊂X→Y是一个指标为零的Fred⁃holm算子，连续算子N:Ω⊂X→Y如果满足：

（I）Kp(I-Q)N()是X的相对紧子集，

（II）QN()是Y的有界子集，则称N在中是L-紧的.

因为ImQ与kerL是同构的，所以存在同构映射J:ImQ→kerL.

引理1［1］（重合度拓展定理）设X,Y为Banach空间，L为指标为零的Fredholm算子，Ω是X中的有界开集，N在上是L-紧的.假设下列条件成立：

（1）Lx≠λNx,x∈∂Ω⋂DomL,λ∈(0,1)；

（2）QNx≠0,x∈∂Ω⋂kerL；

（3）deg{JQN,Ω⋂kerL,0}≠0，其中J:ImQ→kerL为同构映射.

则方程Lx=Nx在DomL⋂中至少存在一个解.

2 主要结果

定理1对于系统（1.2），假设

则系统(1.2)至少有4个ω-周期正解.

证明对系统（1.2）引入一个变量变换，

直接计算得

显然系统（2.1）是等价于系统（1.2）的.为完成定理1的证明，只需要证明在定理1的条件下，系统（2.1）至少有4个ω-周期解.取

则X,Y是两个具范数或Y的Banach空间.

定义线性算子L，P和Q有如下形式，

令N:X→Y满足，

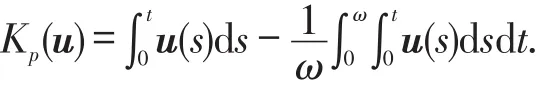
直接计算可得

和

其中

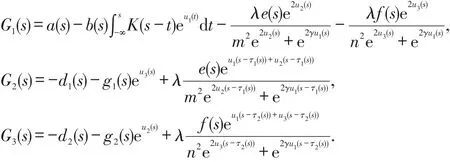
因此，利用Lebesgue定理可知,QN和Kp(I-Q)Nu是连续的.对任意Ω⊂X的有界开集，可用Ascoli-Arzela定理得是紧的. 因此，Q(有界. 所以，N在上是L-紧的.

为完成定理1的证明，需要在X中找出至少4个合适的有界开子集Ωi(i=1,2,3,4).为此，我们考虑算子方程Lx=λNx,λ∈(0,1)，

假设u(t)=(u1(t),u2(t),u3(t))⊺∈X是系统（2.2）的一个解.把系统（2.2）两边同时在区间[0,ω]上积分，可得

由式（2.2）—（2.5）可知

类似的，可得

显然，对于u(t)=(u1(t),u2(t),u3(t))⊺∈X，存在ζi,ηi∈[0,ω]使

从而

对于系统（2.2），有

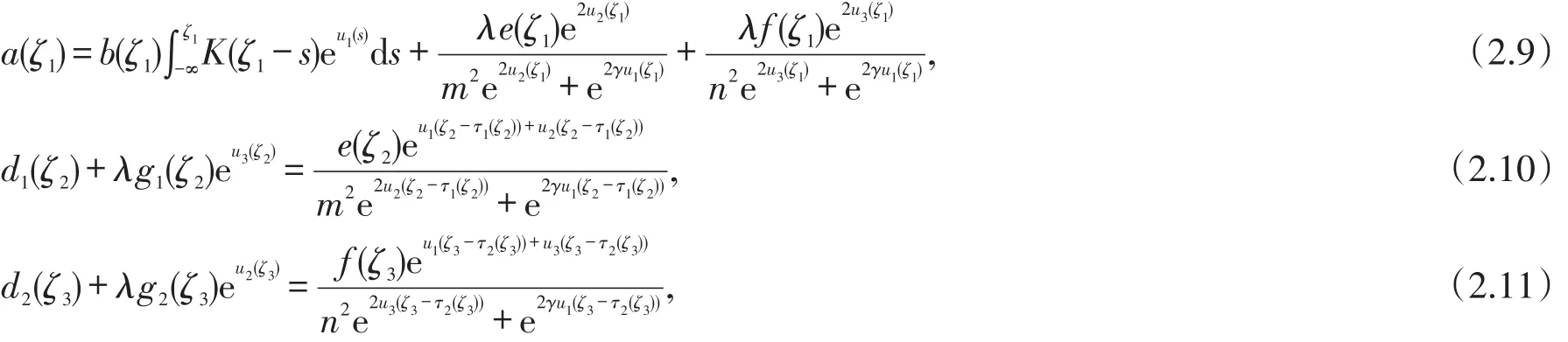
和

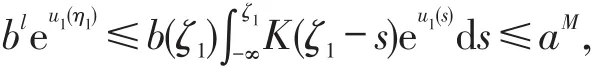
和

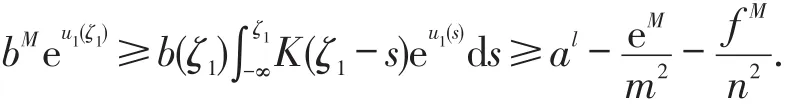
从而有

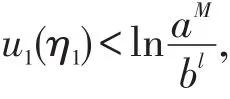
和

对于任意的t∈[0,ω]，有

和

这意味着

由式（2.10），（2.15）和（2.16），可知

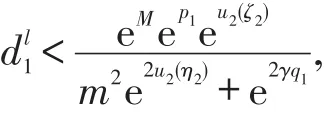
即

因此，对于所有的t∈[0,ω]，可知

在（2.18）中，令t=η2得

上式可改写成

此意味着

进一步可得

其中α±如引言中定义.相似于（2.19），在［H3］下易得

明显地，对所有的t∈[0,ω]，有

（2.13）式表明

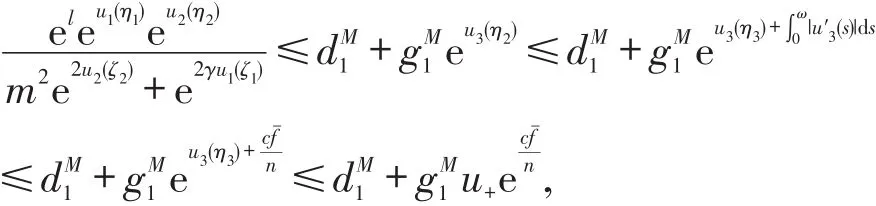
从而

利用（2.23）式可得

因此

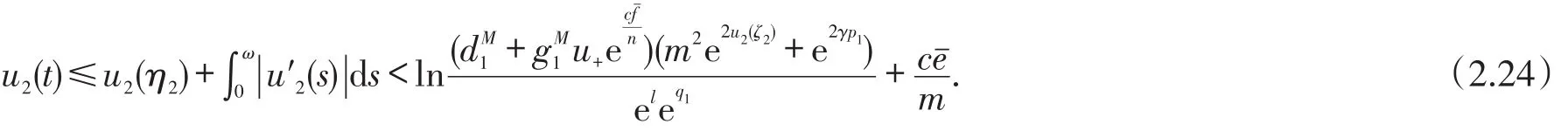
类似于（2.19）式，有

由（2.14）式可知

从而

因此

令t=ζ3可得

利用（2.26）和（2.27）式，可知

接下来，验证引理1中的条件成立.

首先，对于u(t)=(u1,u2,u3)T∈ℝ3，考虑QN(u,0).

在条件［H2］—［H5］，可以证明QN((u1,u2,u3)T,0)=0有4个不同的解，这4个解可表示如下：

显然，lnα±,lnβ±,lnδ±,lnu±,H21,H31和R1全与λ无关.从而可取C∈ℝ+使得现在，构造如下4个开集

因此，Ωi⊂X是满足Ωi⋂Ωj=Ø,i≠j,i,j=1,2,3,4的有界开集.因此引理1中的条件是满足的.易得u1∈Ω1,u2∈Ω2,u3∈Ω3,u4∈Ω4. 从而关于u∈∂Ωi⋂kerL=∂Ωi⋂R3,i=1,2,3,4，有QN(u,0)≠0. 直接计算可得

其中J是满足ImQ=kerL的同构映射.至此，我们证明Ωi满足引理1中的所有假设.所以，系统(2.1)至少有4个ω-周期解ui(t)∈Ωi,i=1,2,3,4.显然，对于i≠j(i,j=1,2,3,4),ui(t)和uj(t)全是不同的.从而证明定理1.

注1本文推广文献［9］对系统（1.1）的结果.

注2如果，则无法使用引理1去解出系统(2.1)有一个ω-周期正解.

注3定理1，注1和注2告诉我们系统（1.2）的解的个数依赖于参数γ.

3 应用

本部分将给出主要结果的一个应用.

例 在系统（2.1）中，如果取

利用Maple17辅助计算，容易得出定理1中的所有条件都成立.因此，通过定理1，系统（2.1）至少存在4个周期正解.

［1］CHEN Lan.Mathematical ecology models and research methods［M］.Beijing：Science Press，1988.

［2］GAINES R E，MAWHIN J L.Coincidence degree and nonlinear differential equations［M］.Berlin：Springer-Verlag，1977.

［3］XIA Yonghui.Global analysis of an impulsive delayed Lotka-Volterra competition system［J］.Commun Nonlinear Sci Num⁃er Simul，2011，16（3）：1597-1616.

［4］LU Shiping.On the existence of positive periodic solutions to a Lotka-Volterra cooperative population model with multiple delays［J］.Nonlinear Anal，2008，68（6）：1746-1753.

［5］FANG Hui，XIAO Yongfeng.Existence of multiple periodic solutions for delay Lotka-Volterra competition patch systems with harvesting［J］.Appl Math Model，2009，33（2）：1086-1096.

［6］MOUSSAOUI A，BASSAID S，DADS E H A.The impact of water level fluctuations on a delayed prey-predator model［J］.Nonlinear Anal,2015，21：170-184

［7］LIU Guirong，YAN Jurang.Positive periodic solutions of neutral predator-prey model with Beddington-DeAngelis function⁃al response［J］.Comput Math Appl，2011，61：2317-2322.

［8］LIN Guojian，HONG Yiguang.Periodic solutions in nonautonomous predator-prey system with delays［J］.Nonlinear Anal RWA，2009，10：1589-1600.

［9］FENG Jianwen，CHEN Shihua.Four periodic solutions of a generalized delayed predator-prey system［J］.Appl Math Com⁃put，2006，181：932-939.

［10］WANG Qi，FANG Yayun，LU Dicheng.Existence of four periodic solutions for a generalized delayed ratio-dependent predator-prey system［J］.Appl Math Comput，2014，247：623-630.

［11］ZHANG Guodong，SHEN Yi.Periodic solutions for a neutral delay Hassell-Varley type predator-prey system［J］.Appl Math Comput，2015，264：443-452.

［12］DING Xiaoquan，JIANG Jifa.Positive periodic solutions in delayed Gause-type predator-prey systems［J］.J Math Anal Ap⁃pl，2008，339：1220-1230.

［13］LIU Guirong，YAN Weiping，YAN Jurang.Positive solutions for a class of neutral delay Gause-type predator-prey system［J］.Nonlinear Anal，2009，71：4438-4447.

Multiple Positive Periodic Solutions in Qeneralized Delayed Predator-prey System with Non-monotonic Functional Responses

KONG Deyu,LIANG Feng,WANG Hao
（School of Mathematics&Computer Science，Anhui Normal University，241002，Wuhu，Anhui，China）

In this paper，we study the existence of multiple positive periodic solutions to a generalized de⁃layed predator-prey system with non-monotonic functional responses.By using Mawhin’s continuation theo⁃rem of coincidence degree principle，some new results are obtained.It is interesting that the number of solu⁃tions is related to a parameter，which is different from the corresponding ones of the known paper.

positive periodic solution；predator-prey system；Fredholm mapping；Mawhin′s continuation theorem.

O 193

A

2095-0691（2017）04-0007-09

2017-05-31

国家自然科学基金项目（11671013）；安徽省自然科学基金项目（1308085MA08）

孔德玉（1990- ），女，安徽霍邱人，硕士生，研究方向：常微分方程与动力系统.通信作者：梁 峰（1974- ），男，安徽太和人，博士，教授，研究方向：常微分方程与动力系统.