二阶变系数线性微分方程的一类通解

2017-12-20叶永升

淮北师范大学学报(自然科学版) 2017年4期

关键词：淮北二阶常数

王慧，叶永升

（淮北师范大学数学科学学院，安徽淮北 235000）

二阶变系数线性微分方程的一类通解

王慧，叶永升

（淮北师范大学数学科学学院，安徽淮北 235000）

文章利用待定函数法，把二阶变系数线性微分方程y″+p(x)y′+q(x)y=f(x)降为一阶线性微分方程，从而推导出二阶变系数线性微分方程的一类通解为，其中C1，C2为任意常数，k为常数，并证明该通解存在的充要条件是p(x)+(x+k)q(x)=0，同时还得出特殊情形的相应结果.

变系数；线性；微分方程；通解

0 引言

变系数线性微分方程不仅在常微分方程理论方面具有重要价值，而且在物理学、化学、自动控制以及电子技术等方面也具有重要作用.在变系数线性微分方程求解问题中，对于阶数较高的微分方程，可以通过降阶法，将其转化为阶数较低的微分方程求解，因此，低阶方程的求解非常重要，特别是二阶变系数线性微分方程的研究一直备受关注.此类方程的通解求法一般是比较困难的，没有普遍适用的方法可循，但当其系数满足某些特定条件时，其通解是可求的.文献［1-10］是近年来关于此类方程求解问题的研究成果，研究思路大体一致，即通过变量代换的思想方法，把二阶变系数线性微分方程降为一阶微分方程或者是转化为二阶常系数线性微分方程，从而得到二阶变系数线性微分方程的可解类型或通解存在条件.本文将利用待定函数法，进一步讨论二阶变系数线性微分方程的通解形式，寻找通解存在的充要条件.

1 预备知识

称为二阶变系数线性微分方程.若f(x)≡0时，方程（1）变为

方程（2）称为与方程（1）对应的二阶变系数齐次线性微分方程.若f(x)≠0，方程（1）称为二阶变系数非齐次线性微分方程.

引理1［11］若p(x)，q(x)为x的连续函数，则一阶线性微分方程y′+p(x)y=q(x)的通解为

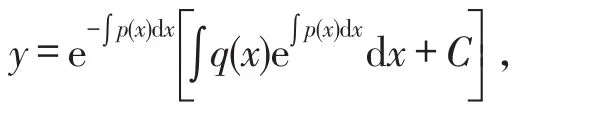
为证明本文主要结论的需要，下面介绍相关定义及引理.

定义1［11］若p(x)，q(x)及f(x)为x的连续函数，则方程

其中C为任意常数.

2 主要结论

定理1二阶变系数非齐次线性微分方程（1）有通解

的充要条件是p(x)+(x+k)q(x)=0，其中C1，C2为任意常数，k为常数.

证明为了简便，不妨记，则（3）式可写为

必要性：若（3）式是方程（1）的通解，则

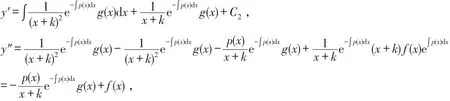
将y,y′,y″代入方程（1），得

化简，得

充分性：设y=(x+k)u(x)是方程（1）的解，其中u(x)为待定的二阶可导函数，k为常数，则

将y,y′,y″代入方程（1），整理可得

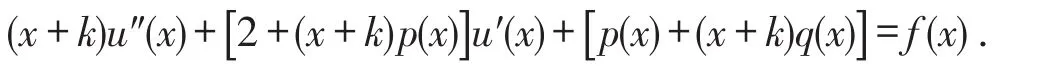
由于p(x)+(x+k)q(x)=0，得

这是一个以u′(x)为未知函数的一阶非齐次线性微分方程，由引理1知，其通解为

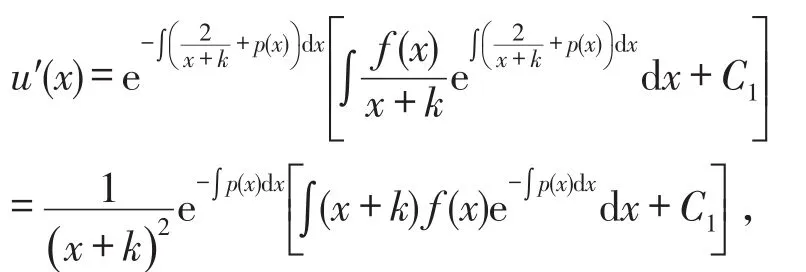
两边积分，得

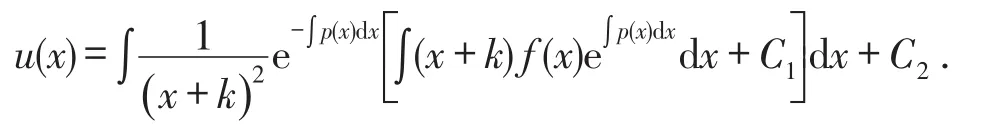
故原方程的通解为

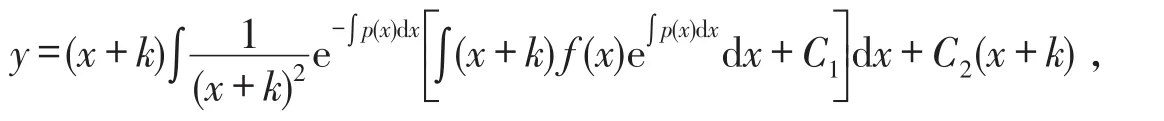
其中C1，C2为任意常数，k为常数.

由定理1，可以得到以下推论.

推论1二阶变系数非齐次线性微分方程（1）有通解

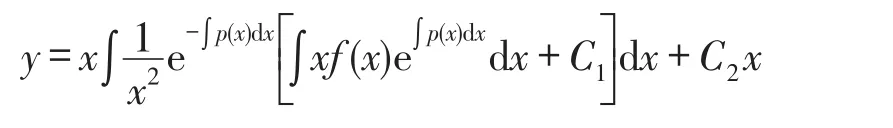
的充要条件是p(x)+xq(x)=0，其中C1，C2为任意常数.

推论2二阶变系数齐次线性微分方程（2）有通解

的充要条件是p(x)+(x+k)q(x)=0，其中C1，C2为任意常数，k为常数.

推论3二阶变系数齐次线性微分方程（2）有通解

的充要条件是p(x)+xq(x)=0，其中C1，C2为任意常数.

3 应用举例

例1求微分方程的通解，k为常数.

解该方程是二阶变系数非齐次线性微分方程，这里

满足条件p(x)+(x+k)q(x)=0，由定理1知，方程的通解为

其中C1，C2为任意常数.

例2求微分方程的通解，其中n为常数.

解该方程是二阶变系数齐次线性微分方程，这里

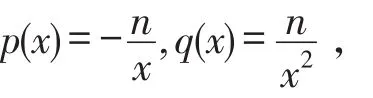
满足p(x)+xq(x)=0，由推论3知，方程的通解为

其中C1，C2为任意常数.

4 结束语

变系数线性微分方程在实际生活中应用广泛，但是其通解形式一直很难求，本文利用待定函数法，把二阶变系数线性微分方程降为一阶线性微分方程，推出二阶变系数线性微分方程的一类通解形式，并证明该通解存在的充要条件.

［1］李高，常秀芳.关于二阶变系数线性常微分方程求解法的研究［J］.大学数学，2010，26（2）：12-14.

［2］杜庆.二阶变系数线性非齐次微分方程的通解［J］.天津工程师范学院学报，2010，20（4）：48-50.

［3］杨万顺.二阶变系数线性常微分方程的求解［J］.潍坊学院学报，2011，11（2）：62-64.

［4］张玉兰.二阶变系数齐次微分方程的通解［J］.长沙大学学报，2013，27（2）：1-3.

［5］张玉兰.一类二阶变系数线性微分方程的通解［J］.佳木斯大学学报（自然科学版），2013，31（4）：638-639.

［6］高杨，王贺元.一类二阶变系数线性微分方程的解法［J］.高等数学研究，2014，17（1）：81-82.

［7］孙瑞.变系数微分方程的解法［J］.九江学院学报（自然科学版），2015，30（1）：56-60.

［8］孙杰华，杜超雄.一类二阶变系数线性微分方程解的研究［J］.邵阳学院学报（自然科学版），2016，13（1）：19-22.

［9］文武.一些特殊类型的变系数二阶线性微分方程解法的研究［J］.大学数学，2016，32（4）：106-113.

［10］文武.二阶变系数线性微分方程通解的进一步研究［J］.四川文理学院学报，2016，26（5）：7-12.

［11］王高雄，周之铭，朱思铭，等.常微分方程［M］.3版.北京：高等教育出版社，2006.

General Solution of Second Order Linear Differential Equations with Variable Coefficients

WANG Hui，YE Yongsheng
（School of Mathematical Sciences，Huaibei Normal University，235000，Huaibei，Anhui，China）

In thispaper，the second orderlineardifferentialequationswith variable coefficientsy″+p(x)y′+q(x)y=f(x)are reduced to the first order linear differential equations by using the undetermined function methods.Next，this paper derived out a sufficient and necessary conditionp(x)+(x+k)q(x)=0for the second order linear differential equations with variable coefficients existing a general solution as the form