移动焊接机器人焊缝跟踪控制系统设计
2017-12-20
(云南机电职业技术学院,昆明 650203)
移动焊接机器人焊缝跟踪控制系统设计
李林会李琳
(云南机电职业技术学院,昆明 650203)
为提高移动焊接机器人的焊缝跟踪精度,结合RBF神经网络和PID控制设计了一种焊缝跟踪控制系统。介绍了焊接机器人系统组成并建立了相应的运动学模型,重点论述了RBF神经网络结构以及控制器的设计方法。通过神经网络在线辨识梯度信息,根据梯度信息在线调整比例、积分、微分系数,以提高系统控制性能。仿真结果表明:采用所述控制方法,能较好地实现复杂轨迹跟踪。在焊缝跟踪过程中,移动焊接机器人运行平稳,具有较高跟踪精度。
焊接机器人焊缝跟踪RBF神经网络PID控制
0 序 言
移动焊接机器人通常具备结构简单、适应性强等特性,所以比较适合非结构作业环境,在大型球罐焊接、造船等领域的应用十分广泛[1-2]。为提高焊缝跟踪精度、确保焊接质量,设计一种性能优良的焊接机器人控制系统具有一定理论和实际意义[3]。然而,现有的控制方法大多以焊接机器人的运动学模型为基础,而且其实际工作环境比较复杂,受机器人本身特性及外部干扰等因素的影响,无法得到满意的控制结果[4-7]。为解决此问题,可以考虑引入智能控制算法。
理想情况下,焊接机器人应具有一定的抗干扰能力和鲁棒性,以保证焊枪沿焊缝中心线稳定运行,同时满足相应的位姿和速度要求[8]。轮式移动焊接机器人是一种典型的非完整约束系统,其约束条件不可积。近几年,结合积分Backstepping方法及Lyapunov稳定性原理受到诸多学者的高度重视,该方法可在一定程度上解决非完整约束系统的轨迹跟踪控制问题[9-10]。但是跟踪过程的平滑度不够,尽管有一些相关改进算法,仍无法解决外界扰动的影响[11]。
在建立移动焊接机器人运动学模型的基础上,设计一种RBF神经网络PID控制器,以实现焊缝跟踪控制。通过仿真验证所述控制方法能够有效改善跟踪效果。
1 焊接机器人
1.1 简 介
移动焊接机器人焊缝跟踪系统主要包括移动机器人、工控计算机、送丝机、弧焊电源、旋转电弧传感器、DA输出卡和数据采集卡等,具体结构如图1所示。其工作过程可以描述为:通过霍尔传感器采集焊接电流的变化,经数据采集卡将其传送至工控计算机;运算处理后,可获得当前时刻焊枪位置偏差和倾角值;经控制器处理后可得到车轮和十字滑块的控制量,经DA转换以实现相应伺服电动机的控制,进而完成焊缝跟踪。

图1 焊接机器人
选用轮式移动焊接机器人,其主要由移动小车和十字滑块构成,具备4个自由度,可对折线、弯曲、直线等类型焊缝进行跟踪。移动小车结构为万向轮前后对称布置,驱动轮位于中间采用差速驱动,十字滑块位于驱动轮轴线上。偏差检测装置采用旋转电弧传感器,可直接作焊枪使用;同时其与十字滑块连接,所以可在水平和垂直两个方向上移动。
1.2 运动学模型
移动机器人运动学模型如图2所示。从图2可以看出:Oxy表示固定坐标系;Cx1y1表示移动坐标系,选取移动机器人中心作为坐标原点。定义机器人中心坐标为(xc,yc)T;移动速度大小为vc;其与x轴夹角为θc;角速度大小为wc;目标位置为r点,对应参考速度大小为(vr,wr)T,其方向与焊缝轨迹切线重合。固定坐标系下,焊枪前端位置可表示为(xw,yw,θw)T。
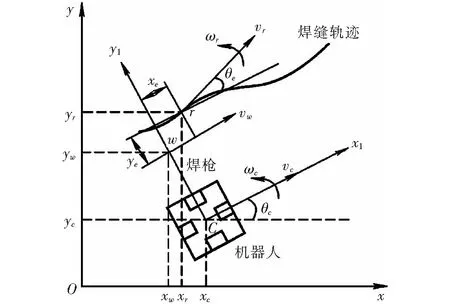
图2 焊接机器人运动学模型
利用n维坐标矢量q=(q1,q2,…,qn)T来描述机器人系统,如果受到m个约束,那么可表示为:
(1)
当运动学模型为非完整约束时,上式可写成:
q=J(q)z
(2)
式(2)中J(q)为n×(n-m)矩阵,同时满足
JT(q)AT(q)=0;z∈Rn-m
(3)
如果移动焊接机器人驱动轮的运动为纯滚动,那么式(1)中A(q)可描述为:
A(q)=(-sinθccosθc0)
(4)
式(2)中速度矢量z可描述为:
z=(vcωc)T
(5)
J(q)可表示为:
(6)
根据轮式移动焊接机器人中心点可得焊枪前端的运动学方程:
(7)
对上式求导可得:
(8)
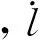
2 RBF神经网络PID控制器设计
结合RBF神经网络和传统PID控制设计了一种控制方法。与传统PID相比,该控制方法具有很好的抗干扰性能;与BP网络相比,同样可以解决输入和输出之间的非线性映射问题,不过其隐含层和输出层之间为线性映射,能够避免局部极小问题而且可以加快学习速度。
2.1 RBF神经网络
对于RBF网络结构,其输入向量可表示为X=[x1,x2,…,xn]T;径向基向量为h=[h1,h2,…,hm]T,其中hj为高斯函数:
(9)
式中,bj表示第j个节点基宽度参数而且非负;cj表示第j个节点的中心矢量的变化量。
RBF网络辨识输出可表示为:
qm(k)=w1h1+w2h2+…+wjhj+…+wmhm
(10)
式中,wj表示网络权向量的变化量。
网络辨识器性能指标函数可表示为:
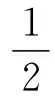
(11)
式中,q(k)表示系统实际输出。基于RBF神经网络的PID控制系统原理如图3所示。梯度信息可通过神经网络在线辨识获得,那么PID控制器三个参数则能够根据梯度信息实时调整,进而适应相关变化,从而提高系统的控制性能。
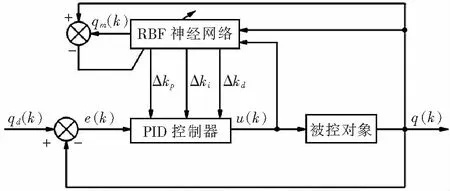
图3 基于RBF神经网络的PID控制系统原理
2.2 控制器设计
定义焊缝跟踪误差为e(k)=qd(k)-q(k),其中qd(k)表示k时刻焊缝位置;q(t)表示k时刻焊枪前端实际位置。
PID控制器的输入可表示为:
(12)
那么PID控制算法可描述为:
u(k)=Δu(k)+u(k-1)
(13)
Δu(k)=kpX1(k)+kiX2(k)+kdX3(k)
(14)
利用RBF神经网络整定PID控制器系数kp,ki,kd,整定性能指标函数可表示为:
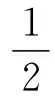
(15)
根据梯度下降法可得到相关调整公式为:
(16)
(17)
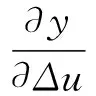
3 仿真研究
为验证所设计控制算法的有效性,文中进行轨迹跟踪仿真试验。设定跟踪轨迹为圆形焊缝,其直径为2 m;移动焊接机器人本体逆时针沿圆弧转动;焊枪期望速度为20 mm/s;本体最大调整角速度为0.02 rad/s;采样周期为0.2 s;机器人焊枪初始位姿为(-5 mm,10 mm,2°)。
设定PID控制器初始参数如下:kp=1,ki=0,kd=0;网络学习速率η1,η2,η3均为0.45。仿真结果如图4所示,其中图4a为轨迹跟踪结果,图4b为焊枪线速度。
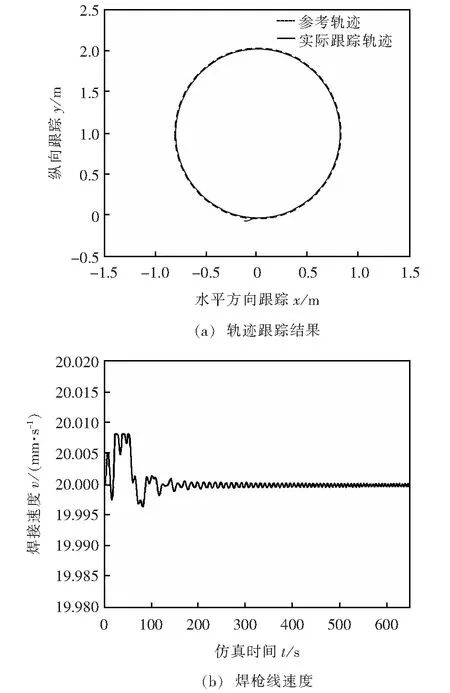
图4 仿真结果
在焊接工作过程中,受工件表面不平、摩擦等因素的影响,驱动轮半径会发生变化。另外,负载变化容易导致系统质量、转动惯量出现变化。同时焊接误差信号具有随机性,所以在仿真过程中将随机干扰信号加入到对应项中。由仿真结果可以看出:焊枪轨迹跟踪误差可以控制在±0.2 mm范围内;焊枪线速度为20±0.02 mm/s,跟踪效果比较理想。
[][]
综上所述,采用所述控制方法能较好地实现复杂轨迹跟踪,而且跟踪精度较高。
4 结 论
(1)移动焊接机器人结构简单,适应性强,比较适合大焊缝、复杂焊缝。简述了移动焊接机器人结构及其运动学模型,结合RBF神经网络和PID控制设计了一种焊缝跟踪控制器,该控制器具有一定抗干扰性。
(2)仿真结果表明:机器人运动性能稳定且具有较高的跟踪精度。移动焊接机器人轨迹跟踪嵌入式控制系统对提高焊接自动化具有一定借鉴意义。
[1] Aghili F. A prediction and motion-planning scheme for visually guided robotic capturing of free-floating tumbling objects with uncertain dynamics[J]. IEEE Trabsactions on Robotics,2012,28(3): 634-649.
[2] 陈洪堂,李海超,高洪明,等. 基于人机工程的主从机器人遥控焊接焊缝跟踪误差分析[J]. 焊接学报,2012,33(5): 9-12.
[3] 高延峰,张 华,毛志伟,等. 轮式机器人折线焊缝跟踪协调控制方法[J]. 焊接学报,2008,29(5): 33-37.
[4] 洪 波,张淇淋,李湘文,等. 移动式焊缝跟踪机器人跟踪精度分析方法[J]. 焊接学报,2012,33(1): 13-16.
[5] 李月华,张 华,叶建雄. 移动焊接机器人及混合控制[J]. 工业控制计算机,2007,20(7): 9-10.
[6] 伍 明,李琳琳,孙继银. 基于概率数据关联交互多模滤波的移动机器人未知环境下动态目标跟踪[J]. 机器人,2012,34(6): 668-679.
[7] 吕学勤,张 轲,吴毅雄. 轮式移动焊接机器人输出反馈线性化控制[J]. 机械工程学报,2014,50(6): 48-54.
[8] 毛志伟,潘际銮,张 华. 狭小空间直角角焊缝移动焊接机器人系统研制[J]. 中国机械工程,2010,21(17): 2040-2043.
[9] 高 胜,常玉连,张瑞杰,等. 基于自由漂浮空间机器人的空间焊缝跟踪[J]. 焊接学报,2008,29(11): 65-68.
[10] Gao Y F,Zhang H,Ye Y H. Back-stepping and neural network control of a mobile robot for curved weld seam tracking[J].Procedia Engineering,2011(15): 38-44.
[11] 吴 勃,许文芳,陈虹丽. 神经滑模控制在机器人轨迹跟踪中的应用[J]. 电机与控制学报,2009,13(1): 99-104.
2017-06-21
TG404
李林会,1964年出生,大学本科,副教授。主要从事自动控制技术及机电一体化技术研究。
