变自由度轮足复合机器人轨迹规划验证及步态研究

牛建业，王洪波※，史洪敏，李 东，李姗姗，吴少振



变自由度轮足复合机器人轨迹规划验证及步态研究

牛建业1,2，王洪波1,2※，史洪敏1，李 东1，李姗姗1，吴少振1

（1. 燕山大学河北省并联机器人及机电系统实验室，秦皇岛 066004； 2. 燕山大学先进锻压成形技术与科学教育部重点实验室，秦皇岛 066004）

为了适应现代化农业对机器人的新要求，该文基于仿生学原理，提出一种可变自由度、轮足复合式、串并混联机构作为四足机器人的腿部机构。该文首先对机器人的整机和腿部机构进行了构形设计，并进行了位置分析；然后，根据农业上的一般地形和障碍物地形，规划了机器人足端普通轨迹及越障轨迹，并利用软件进行了轨迹仿真；其次，根据机器人静态及动态稳定性判据，在保证稳定性的前提下，完成了机器人对角小跑步态规划，并进行了仿真研究；最后，对机器人单腿样机进行了足端轨迹规划验证试验。试验结果表明：该单腿样机可以按给定的轨迹运动，证明该机器人机构设计是可行的，足端运动轨迹规划是正确的。但实际轨迹和理论计算轨迹存在误差，轴方向最大误差2.5mm，轴方向最大误差5.3 mm，误差均小于10 mm，在允许范围内，该机器人能够满足农业现代化的使用需求。

机器人；路径；验证；轮足复合式机器人；变自由度；串并混联机构；步态规划

0 引 言

农业机器人是一种新型多功能农业机械，农业机器人的出现和应用，改变了传统的农业劳动方式，促进了现代农业的发展[1-2]。但是目前常用的农业机器人多为专用型机器人，功能单一、利用率低。同时，由于中国农业逐步向农业企业、家庭农场的模式转变，对农业机器人的性能提出了更高的要求，如地面适应能力强、速度快、载重大、一机多用等[3-4]。轮足复合式机器人以其地面适应能力强、灵活性好，可搭载不同末端执行器的特点，成为国内外机器人领域研究的热点，对于丰富农业机器人的多样性起到积极作用[5]。

查阅国内外文献，现有的轮足复合式机器人根据其结构特点可以划分为以下三类[6]：第一类，目前研究成果较多的是将轮子安装在腿部的末端，使轮子和腿形成串联结构，“以轮作脚”，轮和腿分别具有独立驱动。该结构既可以单独用轮式或足式移动，又可以两种方式混合移动。该结构实际上只是两种移动方式功能上的简单组合，在腿式行走时，机体稳定性不高。如Roller Walker、ATHLETE、Shrimp、Hylos和哈尔滨工业大学研制的机器人HITAN-I[7-11]。第二类，相比第一类而言，该类轮足机器人通过转换机构由轮变成腿，结构简单，运动稳定性好，但是越障能力以及承载能力有限。如Sojourner、Mars Rover、清华大学研制的机器人以及台湾国立大学研制的Quattroped[12-14]。第三类，该类机器人和第一类相比，轮和腿完全分离，既可采用单一方式移动，也可以混合式移动。结构上更加简单，控制更容易，承载能力更大，但是结构尺寸较大，比较笨重。如Leon、Wheeleg以及中国科学技术大学研制的HyTRo-I[15-17]。

通过上述研究分析，对现有的轮足复合式机器人机构进行取长补短，本文提出一种可变自由度、串并混联、轮足复合式机构作为机器人单腿结构。该机构轮和腿可以分别驱动，能实现足式行走和轮式快速行驶2种运动模式。在此基础之上，对机器人腿部机构的足端轨迹规划进行了研究，包括一般情况下足端轨迹及越障情况下足端轨迹两种。基于机器人静态稳定性及动态稳定性判据，对轮足复合机器人进行了对角小跑步态规划及仿真。最后，对机器人单腿样机进行了足端运动轨迹验证。

1 四足机器人机构研究

1.1 整机及腿部机构设计

根据生物学理论，人和动物的骨骼多以串联的方式连接，而大多数骨骼肌以并联方式借助肌腱附着在骨骼上。因此从结构方式上，串并混联机构更接近于生物仿生[18-19]。根据上述理论，本文设计出一种基于变自由度、串并混联、轮足复合式单腿机构的新型轮足复合式机器人，如图1所示。由图1可以看出，该轮足复合式机器人由4个结构相同的机械腿、机架、驱动部分及轮足转换机构等组成。四条机械腿两两对称布置，通过髋部与机架相接，两条前腿的布置相同，两条后腿的布置相同。

1. 左前腿 2. 右前腿 3. 左后腿 4. 右后腿 5.机架 6. 小腿 7. 大腿 8. UPS支链1 9. UPS支链2 10. 髋部

1.1.1 自由度分析

式中为腿部机构的自由度数，为腿部机构的阶数（=6-），为机构的公共约束数，为腿部机构中构件的数目，为腿部机构中运动副的数目，f为腿部机构中第个运动副的自由度数，为腿部机构中的冗余约束数；为腿部机构中的局部自由度数。

每条机械腿有3个自由度，其具体结构为：机械腿通过大腿和2个运动支链（8、9）的3个虎克铰（U副）与髋部相连接，构成一个3支链的并联结构，即（2-UPS+U）机构。其中，2个运动支链（8、9）结构相同，均为UPS支链，其虎克铰端与髋部连接，另一端通过球铰（S副）与大腿相连接，中间部分为电动推杆（P副）即直线驱动器，为腿部机构的主要驱动装置。大腿一端通过虎克铰与髋部相连接，另一端通过转动关节（R副）与小腿串联，该转动关节由电机驱动，从而能够实现机器人小腿的屈伸动作。上述结构中，2个电动推杆模仿动物腿部的骨骼肌分布来驱动大腿两个方向的摆动，然后通过转动关节（R）与小腿串联，整体组成了（2-UPS+U）&R串并混联机构。

大腿采用对开式安装方式，通过筋板和左右侧板组成主体框架，小腿驱动电机和轮足转换机构安装在大腿框架内部，使整体结构更加紧凑，空间利用率高，且便于制造安装和维修。膝关节部分，大腿与小腿之间通过蜗轮轴形成一个转动副，该结构具有运动平稳、承载能力大的优点。轮子安装在膝关节的外侧，此种方式不会像安装在足端那样影响到小腿运动的灵活性。

注：图中O、A1、A2为固定在机架上三个虎克铰的中心点，此三点共面，OA1、OA2分别与机架的两个直角边平行，且OA1⊥OA2，长度分别为a1和a2。B1和C1为两个UPS支链球副的中心，BB1和CC1分别为大腿和两个支链的连接杆，长度分别为b和c，且BB1⊥CC1。l01和l02为两个UPS支链中的移动副，l1为大腿杆长，l2为小腿杆长，K为膝关节中心点，P为足端中心点，M为原点O在地面的投影。在构件看作刚体的基础上，建立了腿部机构的坐标系；α和β为大腿杆绕X轴和Y轴的旋转角度，γ为小腿杆绕Xk轴的旋转角度。下同。

此串并混联、轮足复合式机械腿，使机器人具有2种运动模式。当机器人以腿式运动模式行走时，小腿伸出着地，此时腿部机构具有3个自由度，作为四足步行机器人可跨越障碍，适应非结构地形。当机器人以轮式运动模式行进时，小腿弯曲收回，车轮着地，此时腿部机构为具有2个自由度的并联结构，具有负载大、刚度好的优点。同时，整体重心降低，四个车轮同时驱动，机器人作为四轮移动机器人实现快速行驶。

1.1.2 轮足转换实现方案分析

对于轮足复合式机器人，需要有轮足转换机构来实现轮式行驶和腿式行走方式的快速转换。为了使机器人结构上更加紧凑，将轮足转换机构置于大腿主体内部。如果小腿和车轮分别由电机独立驱动，将会占用较大空间，增加大腿的体积和质量。为了解决这个问题，本文提出一个电机驱动两种行走方式的方案。

该机构主要由驱动电机、传动轴、蜗轮、蜗杆轴、圆锥齿轮、电磁离合器和联轴器等组成。其中，传动轴穿过蜗杆轴内孔（该蜗杆轴沿轴向加工圆形通孔），一端与驱动电机输出轴和电磁离合器1前端固定，另一端通过键与小圆锥齿轮联接，传动轴可在蜗杆轴内孔自由转动。蜗杆轴与电磁离合器1后端通过螺栓固定，并与蜗轮相啮合；蜗轮通过轴承支撑固定在大腿上，并带动小腿实现屈伸动作。小圆锥齿轮与大圆锥齿轮啮合，大圆锥齿轮通过轴承由车轮轴支撑，并和电磁离合器2前端固定，电磁离合器2后端与车轮轴固定，轴端部安装有车轮。轮子和小腿的驱动采用同一个电机，减小了机械机构和控制的复杂性。轮和小腿的传动系统相对独立，采用不同减速比达到各自的速度要求，能够使机器人在行走模式时具有大转矩，而在轮式模式时具有高速性。

1.2 参数设定

通过研究上述国内外现状，并结合现代农业对于机器人速度及载重的要求，本文设计的机器人目标最大载质量为200 kg，最大越障高度200 mm，足式模式下最大速度为1 m/s，轮式模式下最大速度为5 m/s。根据该设计目标经前期对机器人经过运动学分析，工作空间计算，各部尺寸进行优化设计，并建立三维模型，并对电机及电动推杆进行计算和选型。最终给定腿部机构各杆的参数尺寸，以及各输入杆长范围、关节处的动作范围及最大速度，如表1所示。

表1 腿部机构尺寸及运动副参数

1.3 位置分析

机构的位置分析分为位置正解和位置反解[20]。位置正解为已知输入各驱动关节值求解输出端位姿参数[21-22]。在此腿部机构中，并联部分的输入参数为驱动杆01、02的变化值，输出参数为杆1绕固定坐标系的轴和轴的转动角、。而串联部分输入参数为、以及小腿2绕动坐标系K-XYZ的转动角，输出参数为小腿的位姿。

根据几何关系及旋转变换矩阵，可知

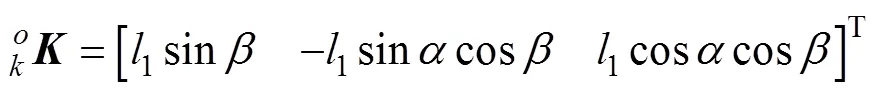
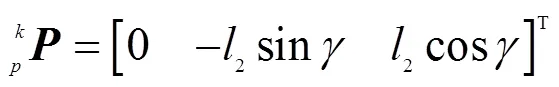
运动坐标系P-XYZ相对固定坐标系的旋转变换矩阵可以表示为

由上述变换矩阵可得足端点处在固定坐标系中的坐标为

根据各点坐标及各坐标系之间的旋转变换矩阵，可以得到两个移动副驱动01、02的长度参数表达式为

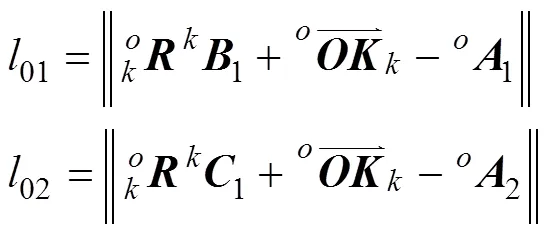
将上式带入相应的值并展开，便可以得到2个移动副驱动01、02的长度计算式

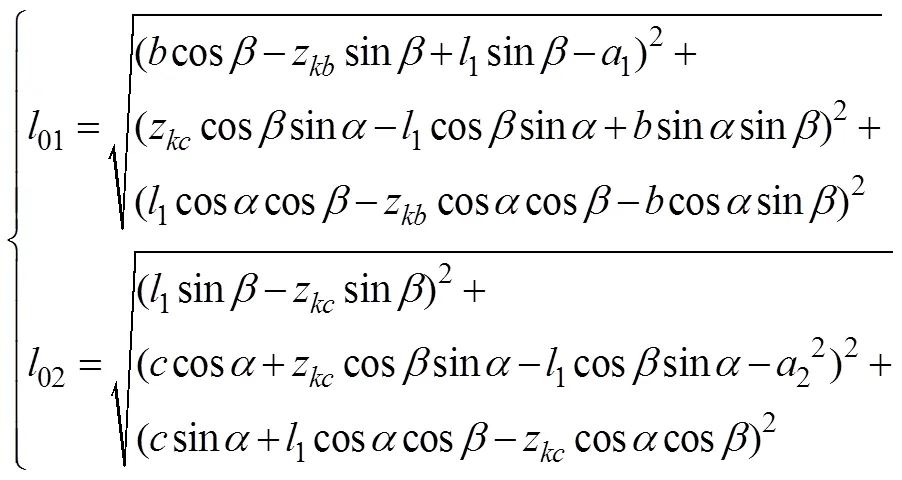
式中z为膝关节到大腿杆点的距离，z为膝关节到大腿杆点的距离。

由此，可将输入参数01、02的值代入（6）式，并将得到的、连同代入（4）式，可以得到足端点在固定坐标中的坐标值（p pp）。此过程为腿部机构的位置正解。

位置反解分析为已知输出参数求输入参数，即已知腿部足端点的位姿，即点在固定坐标中的坐标值（p pp），求解各输入参数01、02和的值。根据几何法在腿部机构中，连接点与点，并向地面作原点的投影，投影点记作，连接、、三点，构造成三角形。如图2所示，在三角形与三角形中，根据三角形余弦定理，可以得到

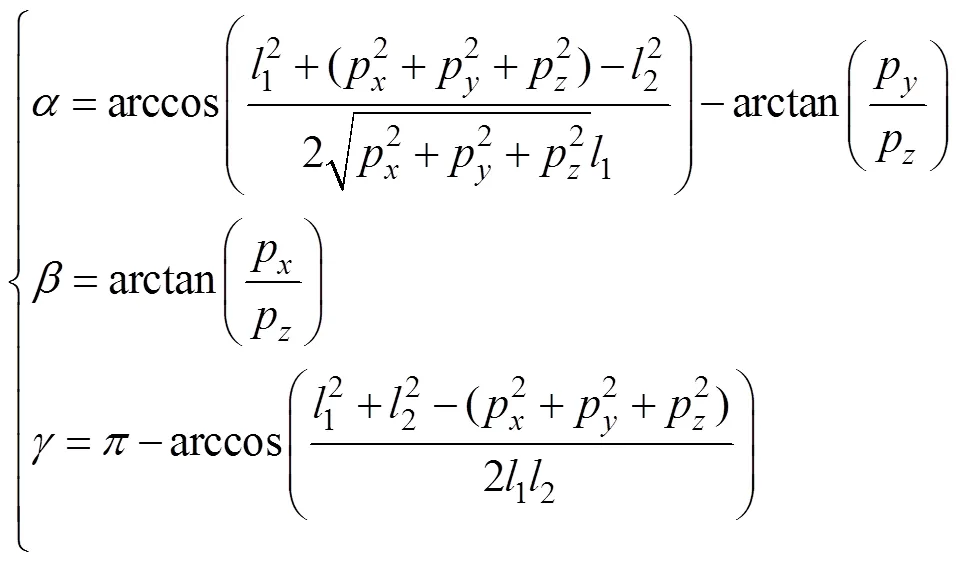
由上式可得、和的值，将得到的、代入式（6）即可得到两个移动副驱动01和02的长度值。

2 四足机器人足端运动轨迹规划

足端运动轨迹规划对于机器人在运动过程中的步幅大小、越障能力、平稳协调性以及是否打滑、拖地等起到决定性作用，需要对其进行深入研究。

机器人在运动过程中，腿部按其所处状态分为摆动腿和站立腿。其中足端离开地面进行迈步动作的腿称为摆动腿；足端与地面接触并保持相对静止来支撑机器人保持站立，实现机体移动的腿称为站立腿，也称作支撑腿。因此，腿机构相应的存在两种运动状态：摆动腿的摆动迈步和站立腿推动机体的移动。摆动腿决定着机器人的歩幅大小和跨越障碍物时的抬腿高度[23]；站立腿支撑着机器人负载，并通过站立腿的驱动实现机器人整体的运动[24]。

2.1 摆动腿足端运动轨迹规划

机器人足端运动轨迹是指足端点相对于地面的运动，即足端点坐标系相对于地面固定坐标系的位姿变化。为规划单腿机构轨迹，首先在腿部运动初始位置建立固定于地面的坐标系，设定初始状态下=15°，=0°，=60°。

机器人在行走时，其足端轨迹是水平方向迈腿和竖直方向抬腿放腿的轨迹合成，因此需要对两个方向的轨迹方程进行规划，保证所有关节都同时到达各指定路径点。由于该机器人四条腿的布置为前后、左右均对称，所以既可以前后行走，即沿图2中轴方向行走；又可以横向行走，即沿图2中轴方向行走。现以向前行走为例，其足端轨迹类似于正弦曲线，前半部分为加速，后半部分为减速，可以分解为轴方向和轴方向两个方向的运动。

轴方向的加速度表达式为

式中A表示幅值，mm；T表示摆动腿的摆动周期，s。

对式（8）进行积分，可以得到轴方向的速度

为了保证足端运动轨迹的平滑，必须对轨迹规划给出以下限制条件：1）腿部机构运行平稳，为保证机构着地无冲击和明显摇晃，足端轨迹在开始和落地时加速度必须为0[25]；2）腿部机构运动轨迹速度和加速度连续无畸点[26]；3）在其工作空间中规划足端轨迹，其弧长合理且易于表达与计算；4）腿部机构在运动过程中与地面之间不产生滑动，且无拖地现象。则腿部机构轨迹规划的约束条件为

式中0表示摆动腿一个迈步周期的步长，mm。

可以得到沿轴方向迈步的运动规律为

若机器人横向行走时，其在水平方向（沿图2中轴方向）的轨迹函数类似于前后行走时水平方向（沿图2中轴方向）的轨迹函数，因此由式（11）同理可得横向行走时轴方向的轨迹函数为

式中1表示摆动腿一个迈步周期的步长，mm。

机器人无论前后行走还是横向行走，其足端在轴方向的轨迹函数相同，分为抬腿和落腿两个阶段。同时，为消除腿的急动和冲击，需同时保证离地和落地两个时刻的速度和加速度为零。因此，采用分段函数进行表示，设三段分段函数为：抬起摆动段1，所用时间为1T；直线段2，所用时间为2T；落下摆动段3，所有时间为3T，且1+2+3=1。可得足端在轴方向的运动规律为

式中0为足端轨迹最高幅值，mm。

对式（13）进行分析可知，当曲线在=T/2时刻，加速度急剧变化，从而惯性力也会急剧变化，导致足端不稳定，振动严重。对其进行修正后，取1=0.25，2=0.5，3=0.25时，得到机器人腿部机构前后行走及横向行走时在高度方向足端运动轨迹规划函数为

2.2 摆动腿足端越障轨迹规划

为了使机器人满足在不平坦的田地上作业，需要对其进行足端越障轨迹规划，使其能跨越不规则的小型障碍物。目前，足端越障轨迹规划方法主要有初等函数曲线组合法和样条插值曲线法。初等函数曲线组合是通过函数参数的调整改变步长和足端提离高度；而样条插值曲线是通过优化插值点改变轨迹形态以实现越障功能，同时可降低轨迹长度，提高平滑性。相比之下，本文将采用插值曲线方法中的关节空间分段多项式曲线进行足端轨迹规划。

在轨迹规划中，首先要简化模型，用相互叠加的圆包络障碍物，并适当地增大包络圆，包络圆直径为1，建立摆动腿越障简化模型，如图3所示。因障碍物高度较低，故只需考虑小腿构件与障碍物的碰撞，将小腿看作有一定直径的圆柱体，其直径为2，并将此直径叠加到包络障碍物的包络圆上，并取一定的安全裕度σ。

摆动腿足端的初始抬腿点为该腿作为支撑腿结束时刻的状态，设初始点坐标为（y z），此时各关节输入角度α、β、γ为已知，可写成矩阵的形式并记作0。设规划的目标足端落地点坐标为（y z），此时各关节输入角度α、β、γ为已知，可写成矩阵的形式并记作，假设障碍物包络圆的圆心坐标为为（y z）和半径r，则有

首先需要定义3个关节在轨迹中间点（=1，…，）的输入参数为变量，其具体表达式为

现以第（=1,，2，3）个关节为例，中间点-1与中间点之间的4次多项式轨迹曲线表式如下

式中a0n~a4n为第个关节、中间点-1与中间点之间多项式的系数，t表示第段轨迹的起始时间，s。

最后一段曲线的轨迹表式如下

注：矩形表示障碍物；虚线圆为包络障碍物的圆，半径为1；实线圆为包络圆与足端实体叠加成的圆，半径为c；1为轨迹曲线中间点，为高度余量；（y z）为起始点坐标，（y z）落足点坐标。

Note: The rectangle represents the obstacle. The dashed circle is the circle for enveloping obstacle, and its radius is1. The solid circle is the circle formed by superposition of the envelope circle and the foot-end entity, and its radius isc.1is the intermediate point of the trajectory curve, andis the height margin. （y z）is the coordinates of starting point, and （y z） is the coordinates of terminal point.

图3 摆动腿越障模型简化图

Fig.3 Simplified diagram of obstacle model for swing leg

根据起始点位置（y z）及落足点位置（y z），可求摆动腿起始点及落足点各关节输入值0和g，并且起始点输入速度及输入加速度须为0。再将起始点的已知条件及第一个中间点的输入关节变量代入，可求得第一段曲线的轨迹曲线，根据第一段轨迹曲线可求得第一个中间点的输入加速度，依次可求得每段的轨迹曲线。

通过逆运动学就可求得关节输入参数，因此，通过搜索变量使足端轨迹达到避障功能。

2.3 轨迹规划仿真

为确定机器人腿部机构初始站立状态的腿部角度，初始状态关节角、需要遵循以下选择原则：1）摆动腿机构抬腿时，机器人在另外三条站立腿的支撑下能保持瞬时的平衡；2）避免摆动腿抬腿时因能量变化大而造成振动冲击；3）支撑机体的站立腿驱动关节使机体前移所需能量小，减小关节间冲击。因此，定义大腿杆件的初始角度=15°，=0°，小腿杆件的初始角度=60°。以常见小型障碍物为例，将其简化为直径100 mm球体的内接不规则多面体，结合电动推杆最大速度为200 mm/s，最终选取足端运动曲线最高幅值0=100 mm，步长0=100 mm，并给定单腿迈步周期为T=0.1s。将腿部机构按照式（11）、式（12）及式（14）所规划的轨迹运动一个周期，并将仿真结果与MATLAB软件中理论运动曲线进行对比。

根据轨迹规划，可求出01、02和的输入值及输入杆速度变化对应的曲线如下图4所示。由于本机构为解耦机构，以沿轴方向前进为例，电动推杆01的变化量为0。

图4 轨迹规划广义坐标输入值

从图中可以看出，02行程变化量及膝关节转动弧度在允许范围内，并且腿部机构输入杆的速度变化范围符合电动推杆及电机的输入速度范围。

图5为单腿在摆动周期中，足端点相对于地面坐标系在各个方向的位移和速度，在MATLAB软件中理论计算曲线和机构在ADAMS软件仿真中得到的仿真曲线的对比。在仿真结果中，腿部机构在满足速度要求的前提下，其抬腿高度为98.2 mm，迈步步长为101.3 mm，可以达到跨越直径小于100 mm的小型障碍物的能力。腿部机构运动速度曲线连续无畸点，总体位移曲线符合腿部足端点抬腿及下落的运动规律，变化平稳，且腿的起、落点与地面间的相对速度为0，抬腿和落腿时加速度为0，消除了腿的急动和冲击，能够实现无冲击和软着陆。通过仿真结果与理论结果对比，抬腿高度和迈步步长误差在2 mm以内，满足使用要求，验证了腿部机构足端运动轨迹规划的正确性，因此该轨迹规划可行。

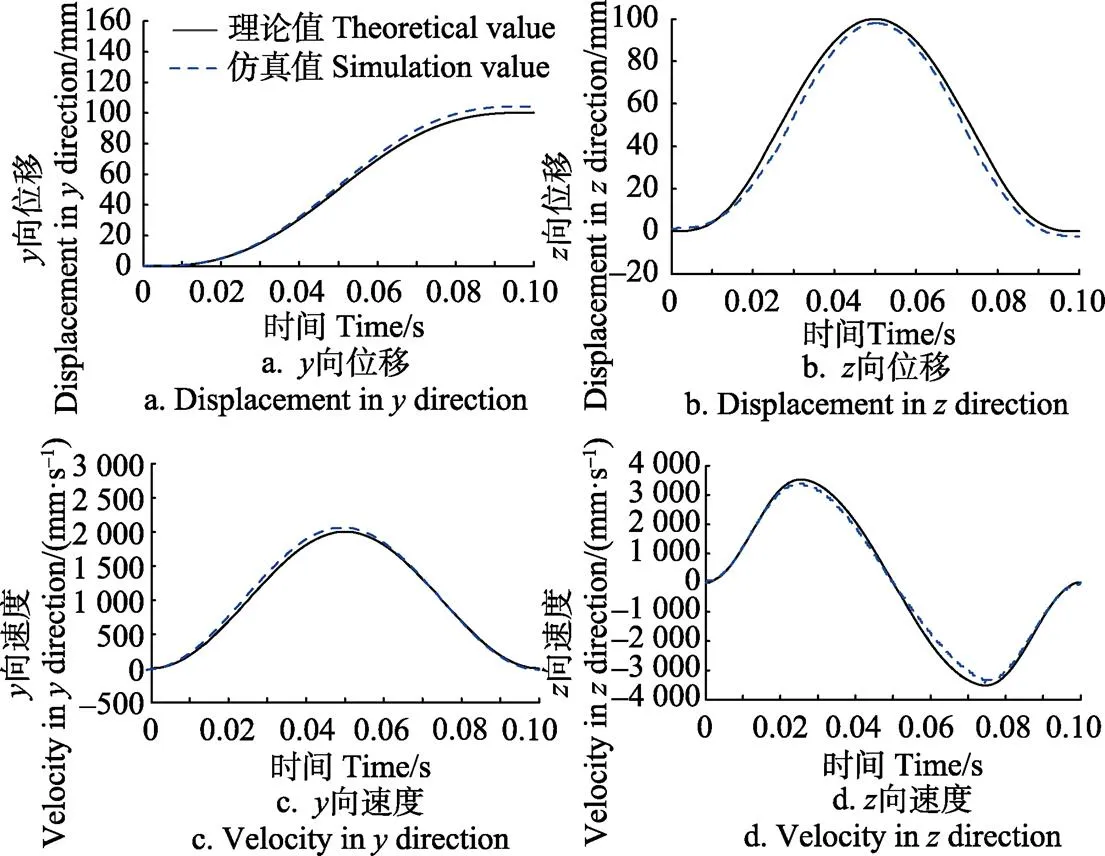
图5 足端轨迹规划理论与仿真对比

3 四足机器人步态研究

3.1 步态规划基本参数

机器人在步态规划前，需定义如下参数：

1）占地系数，占地系数是指机器人腿机构着地时间和一个步态周期（s）的比值。当＞0.5时，机器人任何时刻都至少有三条腿支撑地面，机器人移动速度较慢。当=0.5，机器人始终存在两条站立腿和两条摆动腿，处于对角小跑状态，速度较快。当＜0.5时，机器人在任何时刻支撑在地面的站立腿少于两条，机器人处于跳跃运动状态，速度快。

2）步长：机器人在一个周期内行走的距离，mm。

3.2 稳定性判据

机器人步态研究的前提是保证机器人在农田非结构地形上行走，频繁跨越不规则土块等小型障碍物时的稳定性，即在步态生成时必须进行实时的稳定性计算分析，只有在保证实时稳定性的前提下，机器人才能实现行走要求[27]。本文在考虑机器人稳定性的过程中，主要考虑了以下问题：1）机器人主要应用于不平坦路面，运行路况对于稳定性的影响不能忽略。2）机器人迈步过程中摆动腿的抬起与落下都会影响机器人的重心位置，稳定性受重心位置变化的影响不可忽略。3）机器人的运行速度较快，不可忽略。

机器人稳定性判据分为两大类，分别为静态稳定性判据和动态稳定性判据。本文主要针对农田中不平坦地面的静态步行（＞0.5）及较平坦地面的动态步行（=0.5）进行规划，因此，要考虑各个判据的适用范围，同时采用静态的稳定余量及动态的零力矩点（Zero Moment Point，以下简称ZMP）作为机器人稳定性判据。

3.2.1 静态稳定性

机器人以静态爬行步态前进时，其稳定性可用稳定余量作为评价标准。稳定余量是指机器人重心向着地面作垂线的垂足（重心投影点）位于站立腿支撑点连接所形成的支撑多边形内部，则不会发生翻倒。重心投影点到支撑腿多边形各边的距离可以作为稳定余量的评价量。如图6所示，根据站立腿足端形成的三角形及机体重心的位置，可求得重心到该三角形各边的距离，其中最小值即为稳定余量值[28]。设定23、24、34为各边到重心的距离，通过三边的表达式，可以得到稳定余量d的值为

注：白色圆形表示摆动腿，黑色圆形表示站立腿。

Note：White circle represents the swing leg, and the black circles represents the standing leg.

图6 腿1爬行步态迈步简图

Fig.6 Step diagram of leg 1 in crawl gait

3.2.2 动态稳定性

该机器人动态稳定性选用零力矩点作为稳定性判据，根据其定义零力矩点主要是求解一点使该机构的惯性力及力矩的和为零。该机器人有4条腿，设第（=1,2, 3,4）条腿的第（=1,2,3,4）个杆件的质量为m，加速度为a。其中四个杆件分别为大腿杆、小腿杆、电动推杆01和电动推杆02。机器人机体的质量为m，kg，其加速度为a，mm/s2，在忽略外力及外力矩的情况下，第条腿所受的合力为惯性力和重力之和为

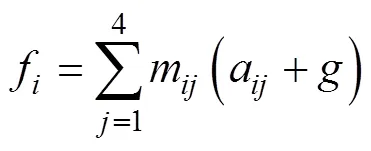
上平台机体所受的惯性力和重力之和为

机器人的重心在固定坐标系中的位置为（x y z），机器人整机总的重力之和为

机器人总的惯性力之和为

式中a、a、a为机器人总体加速度在、、三个方向的分量；a、a、a为机器人第条腿、第个杆件加速度在、、三个方向的分量；a、a、a为机器人机体加速度在、、三个方向的分量。

将所有腿部机构及机体的惯性力及重力等效为重心处的惯性力及重力，并假设机器人零力矩点的坐标为（ZMPZMP），则根据零力矩点的定义，可以求得其位置坐标为

式中x、y、z为重心坐标，a、a为机器人总体加速度在、方向的分量。当机器人动态步行时，由于惯性力的作用机器人的重心可能移动到稳定区域的外部，但要保证ZMP在稳定区域之内。

3.3 动态步态规划

为了使机器人达到快速行走的目的，机器人应采用动态步行，本文将规划动态步行中的对角小跑步态[29]。在规划对角小跑步态时，通过重心控制，使重心和惯性力的合力向量通过支撑腿着地点的连线。

首先将机器人各腿进行编号：左前腿编号为1，左后腿编号为2，右后腿编号为3，右前腿编号为4；并将对角上的两条腿分为一组，即腿1和3一组，腿2和4一组。因此，对角小跑步态可分为两种，即（1、3）→（2、4）步态和（2、4）→（1、3）步态[30]。下面对第一种步态进行分析，顺序为（1、3）→机体前移→（2、4）→机体前移→（1、3），如图7所示[31]。在=0 s时，腿1、3处于摆动相的0相位，支撑相的2π相位，即将开始迈步；腿2、4处于支撑相的0相位，摆动相的2π相位，即将开始支撑。

注：白色矩形表示腿部处于摆动相，灰色矩形表示腿部处于支撑相，黑色矩形表示支撑腿推动机体前移。

假设摆动腿向前迈1个步长所用时间为/2，=2s，机体向前移动半个步长所用时间为4。起始时刻，机器人处于四腿站立状态。在=0~/2期间，腿1和腿3成为摆动腿，并向前迈出1个步长，另外两条腿2和4站立支撑机体。其中当=0~/4期间，此时机器人重心位置在站立腿的对角线上；当=/4~/2期间，由于摆动腿1和3将要完成向前跨步的动作，此时机器人重心因为摆动腿的前移而有摔倒趋势，为使机器人保持稳定状态，站立腿2和4一边支撑机体，一边驱动相应的输入关节，推动机体向前平移/2；=/2时刻，机体移动到位，摆动腿1和3完成一个步长的跨步，即将变为站立腿，原站立腿2和4即将变为摆动腿。=/2~期间，摆动腿2和4完成向前一个步长的迈步，同时腿1和3站立支撑机体。此过程中，站立腿1和3支撑机体并驱动相应输入关节使机体前移/2，使机器人重新恢复稳定状态。上述整个过程为机器人对角小跑步态的一个完整周期。

为保证机器人在田间较平坦地面能实现快速小跑以提高行进效率，并能够保持动态稳定性，对机器人对角小跑步态按以下具体步骤规划：

1）ZMP点的轨迹曲线

根据对零力矩点理论的分析可知，机器人的ZMP点必须落在站立腿的对角线上，根据图6所示的坐标系，机器人站立腿对角线方程可以根据直线系数方程求得

式（26）为机器人ZMP点所在的曲线，可直接作为机器人ZMP点拟合的曲线。

2）规划机器人重心位置

根据得出的机器人ZMP点位置的计算公式，变换其方程可以得到

解上式微分方程可以得到

机器人对角小跑步态规划中，由于腿1与腿3膝关节方向不同，腿2与腿4膝关节方向不同，所以其足端轨迹函数不同。摆动腿向前跨步过程中，由于站立腿驱动输入关节使机体向前平移/2，所以摆动腿足端相对于固定坐标系向前移动/2。根据文中轨迹规划函数可知，机器人向前运动时，前腿作为摆动腿足端点运动轨迹曲线的函数为

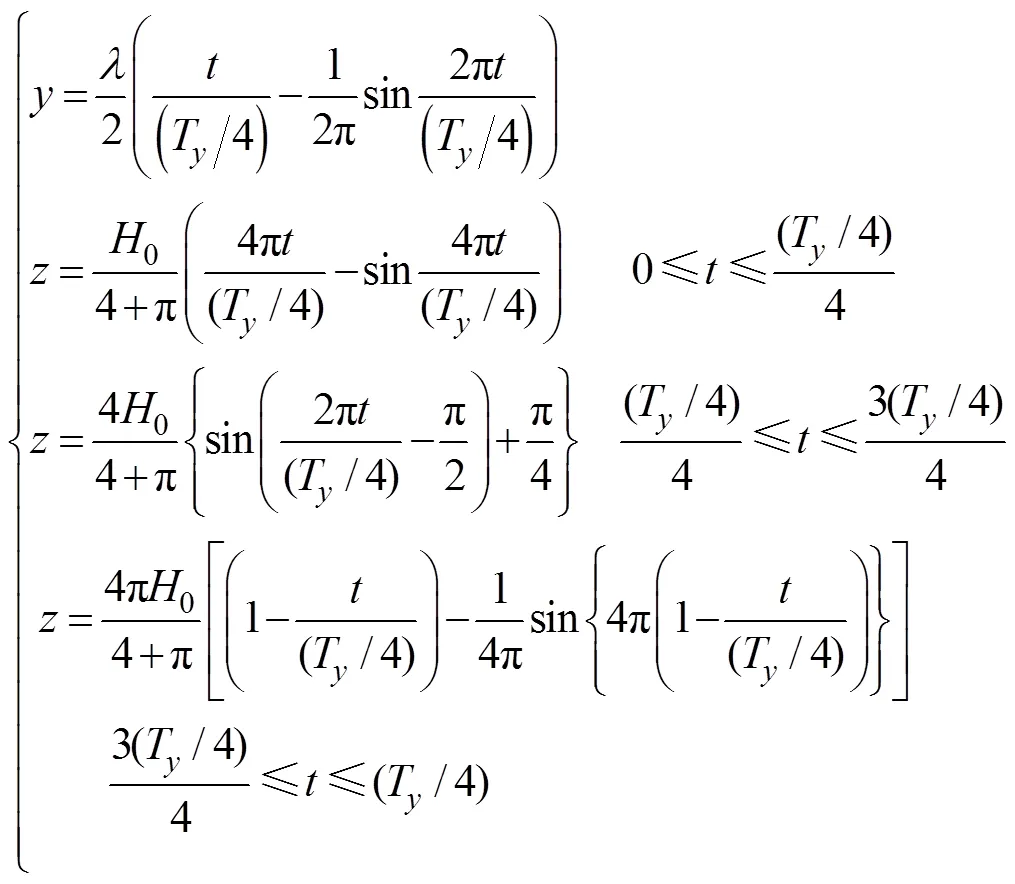
后腿作为摆动腿足端点运动轨迹函数在轴方向与前腿运动轨迹函数一致，方向轨迹函数为

上述摆动腿足端运动轨迹曲线为足端点的位姿在足端点与地面接触点处固定坐标系中的函数描述，应用逆运动学理论，可将足端点处期望的位姿函数转换成期望的输入关节角。

在摆动腿跨步时，机器人站立腿驱动关节使机体向前平移，所以站立腿的轨迹相对于地面接触点处固定坐标系的坐标为（s s s），其表达式为

式中表示平台移动速度，表示平台高度。

根据站立腿逆运动学计算，可将足端点位姿函数转换成期望的输入关节角。

机器人控制系统通过控制输入关节的输入值，使其按规划的各段关节轨迹平滑运动，并协调各关节间的运动，便可完成机器人对角小跑步态。

3.4 步态仿真

为在ADAMS中进行建模，将机器人整机模型及单腿模型从SolidWorks中导入ADAMS中，添加各运动副的运动约束及足端与地面的接触力和摩擦力，最后针对机器人的动态步态进行仿真。

机器人对角小跑步态仿真如下图8a～8d所示。可以看出，机器人在对角小跑步态时，其迈步稳定，机体移动速度较快。图8e所示为机器人机体重心的位置变化，可以看出，机器人机体重心变化约为0.9 mm，重心变化很小。重心基本不随机器人的移动而变化，足以保证机器人在对角小跑步态时，不会因为重心起伏造成机器人稳定性很差。

图8 机器人整机对角小跑步态仿真

4 轨迹规划试验

为了验证设计的可行性，制作了机器人的单腿样机，该样机由机械本体、2个电动推杆和1个电机、3块控制器、3块驱动器、2个电源模块和上位机组成，如图9所示。经过前期计算分析，选用的电动推杆01最大行程125 mm，最大推力11kN，最高速度200 mm/s。电动推杆02最大行程200 mm，最大推力15.6 kN，最高速度200 mm/s。膝关节驱动电机额定电压为48 V、额定功率400 W、额定转矩0.8 N·m、峰值转矩1.6 N·m、额定电流11 A、额定转速4 500 r/min、空载转速5 900 r/min。

机器人单腿轨迹规划试验是机器人整机步态试验的基础，所以本文对单腿样机进行了轨迹规划验证试验。具体试验过程如下：

1）根据本文对腿部机构位置的正反解及轨迹规划，得到理论数据并导入控制软件，使单腿样机做出迈步动作，如图9a～9g所示。

2）在单腿样机足端点测量处放置反射球，并能使激光打在反射球上。采用激光跟踪仪对样机足端点的运动轨迹进行跟踪测量。

3）使用手持式测量传感器测量腿部机构足端点的位置，重复试验五次并保存采集数据，最终在上位机轨迹输出界面输出实际轨迹曲线。

4）将理论数据利用MATLAB软件生成理论曲线，并对比理论计算轨迹和实际轨迹的重合度，如图9h所示。

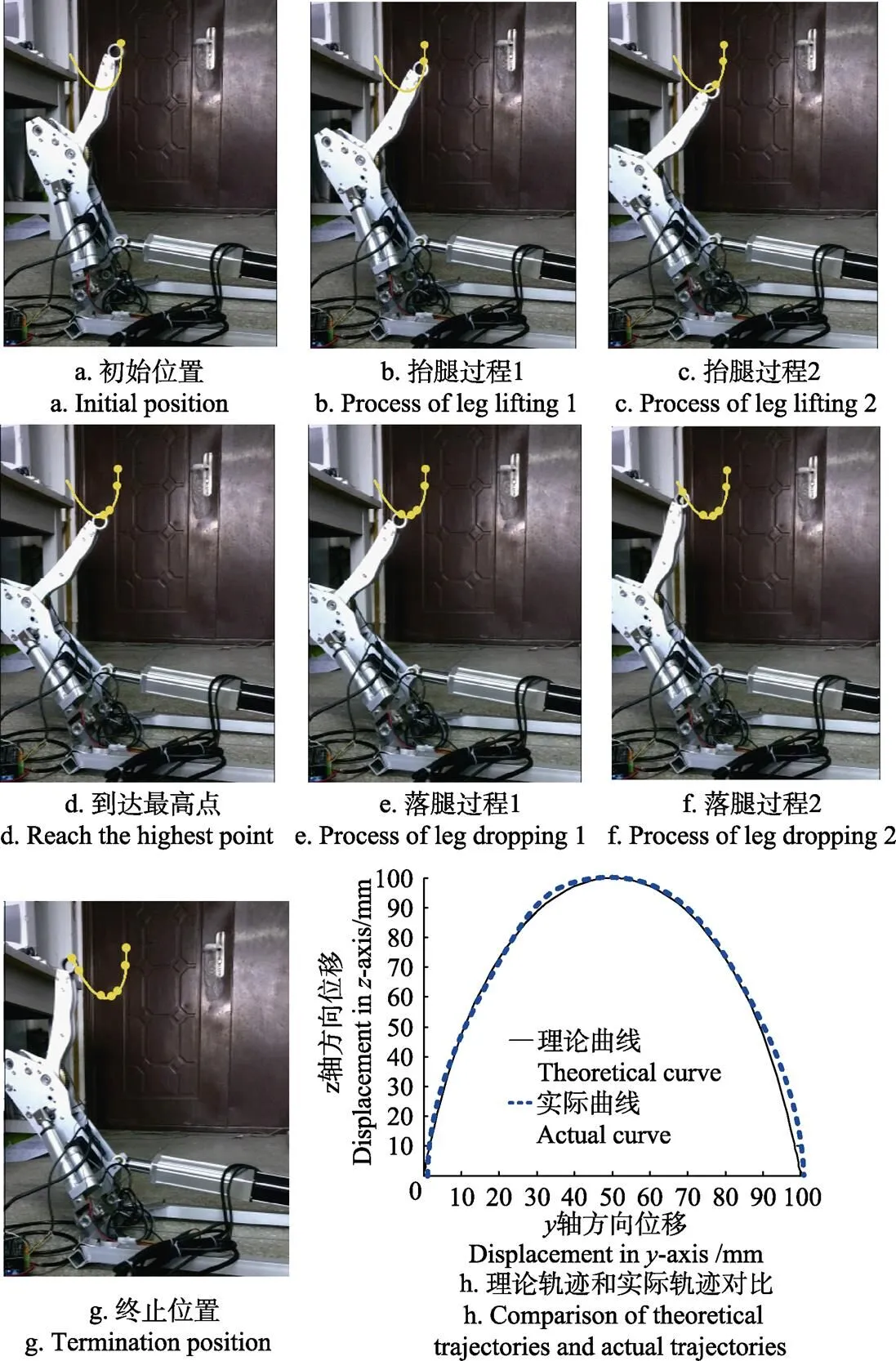
图9 机器人单腿轨迹规划试验结果

在上述试验中，机器人单腿样机能够按照前文规划的越障轨迹完成整套动作，且动作连续、比较平稳无大的波动。验证了机构设计的可行性，输入关节在其运动范围内，无卡死现象。通过对比足端运动实际轨迹与理论轨迹可以看出，两者基本重合，但存在误差。最大误差出现在落脚处，轴方向最大误差2.5 mm，轴方向最大误差5.3 mm，误差均小于10 mm，在误差允许范围内，该误差主要来源于机构的加工误差和装配误差。

5 结 论

本文提出了一种基于（2-UPS+U）&R机构的轮足复合式、串并混联四足机器人，该机械腿为可变自由度机构，具备轮式和足式两种运动模式。该机器人可以在不同的地形作业，可以搭载多种不同的末端执行器，适应不同的作物，提高机器人的利用率，可避免功能单一的缺点。对机器人腿部机构一般足端轨迹及越障足端轨迹进行了规划和仿真。在越障足端轨迹仿真结果中，其抬腿高度为98.2 mm，误差为1.8 mm；迈步步长为101.3 mm，误差为1.3 mm，得出机器人能够翻越小型障碍。基于机器人静态及动态稳定性判据，对机器人进行了对角小跑步态规划，并通过ADAMS软件进行了仿真分析，机体重心高度变化约为0.9 mm，证明机器人可以在该步态下稳定行走。最后，对机器人单腿样机进行了轨迹规划试验，该单腿样机可以按给定的轨迹运动，验证了机构设计的可行性。通过轨迹跟踪试验，发现理论计算轨迹和实际轨迹存在误差，轴方向最大误差2.5 mm，轴方向最大误差5.3 mm，误差均小于10 mm，在误差允许范围内，该误差主要来自加工和装配误差。

今后将完成机器人整体样机的制作，进一步提高加工和装配的精度。进行转弯步态、爬阶梯步态的规划，并利用整体样机对规划的各种步态及其稳定性进行试验验证。

[1] 朱凤武，于丰华，邹丽娜，等. 农业机器人研究现状及发展趋势[J]. 农业工程学报，2013，29(6)：10－13. Zhu Fengwu, Yu Fenghua, Zou Lina, et al.Research status quo and future perspective of agricultural robots[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE),2013, 29(6): 10－13.(in Chinese with English abstract)

[2] 王儒敬，孙丙宇. 农业机器人的发展现状及展望[J]. 中国科学院院刊，2015，30(6)：803－809. Wang Rujing, Sun Bingyu. Development status and expectation of agricultural robot[J]. Bulletin of Chinese Academy of Sciences, 2015, 30(6): 803－809. (in Chinese with English abstract)

[3] 林欢，许林云. 中国农业机器人发展及应用现状[J]. 浙江农业学报，2015，27(5)：865－871. Lin Huan, Xu Linyun. The development and prospect of agricultural robots in China[J]. Acta Agriculturae Zhejiangensis, 2015, 27(5): 865－871. (in Chinese with English abstract)

[4] 张金柱，金振林，陈广广. 六足步行机器人腿部机构运动学分析[J]. 农业工程学报，2016，32(9)：45－52. Zhang Jinzhu, Jin Zhenlin, Chen Guangguang. Kinematic analysis of leg mechanism of six-legged walking robot[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(9): 45－52. (in Chinese with English abstract)

[5] 曲梦可，王洪波，荣誉. 轮腿混合四足机器人六自由度并联机械腿设计[J]. 农业工程学报，2017，33(11)：29－37. Qu Mengke, Wang Hongbo, Rong Yu. Design of 6-DOF parallel mechanical leg of wheel-leg hybrid quadruped robot [J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(11): 29－37. (in Chinese with English abstract)

[6] 王晓芸. 轮腿复合式救援机器人机构分析与仿真[D]. 秦皇岛：燕山大学，2015. Wang Xiaoyun. Mechanical Analysis and Simulation of a Novel Wheel-Leg Hybrid Rescue Robot[D]. Qinhuangdao: Yanshan University, 2015. (in Chinese with English abstract)

[7] Endo Gen, Shigeo Hirose. Study on Roller-Walker improve­ment of locomotive efficiency of quadruped robots by passi­ve wheels[J]. Advanced Robotics,2012, 26(8/9): 969－988.

[8] Wilcox B H, Litwin T, Biesiadecki J, et al. Athlete: A cargo handling and manipulation robot for the moon[J]. Journal of Field Robotics, 2007, 24(5): 421－434.

[9] Siegwart R, Lamon P, Estier T, et al. Innovative design for wheeled locomotion in rough terrain[J]. Robotics and Autonomous Systems, 2002, 40: 151－162.

[10] Grand C, Benamar F, Plumet F, et al. Stability and traction optimization of a reconfigurable wheel-legged robot[J]. The International Journal of Robotics Research, 2004, 23(10/11): 1041－1058.

[11] Wang Pengfei, Sun Lining. Wheeled foot quadruped robot HITAN-I[J]. High Technology Letters, 2006, 12(4): 346－350.

[12] 韩鸿硕, 陈杰. 21世纪国外深空探测发展计划及进展[J]. 航天器工程, 2008, 17(3): 2－4.

[13] 郭丽峰, 陈恳, 赵旦谱, 等. 一种轮腿式变结构移动机器人研究[J]. 制造业自动化, 2009 (10): 1－6.

[14] Chen Shenchiang, Huang Kejung, Chen Weihsi, et al. Quattroped: A leg-wheel transformable robot[C]//IEEE/ASME Transactions on Mechatronics, 2014, 19(2): 730－742.

[15] Eric Rohmer, Matthew Collins, Giulio Reina, et al. A novel teleoperated hybrid wheel-limbed hexapod for the exploration of lunar challenging terrains[C]//International Symposium on Space Technology and Science. 2008: 3902－3907.

[16] Lacagnina M, Muscato G, Sinatra R. Kinematics, dynamics and control of a hybrid robot Wheeleg[J]. Robotics and Autonomous Systems, 2003, 45(3/4): 161－180.

[17] Lu Dongping Dong Erbao, Liu Chunshan, et al. Design and development of a leg-wheel hybrid robot HyTRo-I[C]// IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2013: 6031－6036.

[18] 王洪波，齐政彦，胡正伟，等. 并联腿机构在四足/两足可重组步行机器人中的应用[J]. 机械工程学报，2009，45(8)：24－30. Wang Hongbo, Qi Zhengyan, Hu Zhengwei, et al. Application of parallel leg mechanisms in quadruped/biped reconfigurable walking robot[J]. Journal of Mechanical Engineering, 2009, 45(8): 24－30. (in Chinese with English abstract)

[19] 桑凌峰.载人四足并联腿步行椅机器人理论与实验研究[D].秦皇岛：燕山大学，2015. Sang Lingfeng. Theory and Experimental Research for Human-Carrying Quadruped Walking Chair Robot with Parallel Leg Mechanism[D]. Qinhuangdao: Yanshan University, 2015. (in Chinese with English abstract)

[20] 文红，李俭. 基于BP神经网络的并联机器人位姿分析[J].成都大学学报(自然科学版)，2013，22(1)：46－49. Wen Hong, Li Jian. The displacement analysis of parallel manipulators based on BP neural network[J]. Journal of Chengdu University (Natural Science Edition), 2003, 22(1): 46－49. (in Chinese with English abstract)

[21] 熊有伦，丁汉，刘恩沧. 机器人学[M]. 北京：机械工业出版社，1993：97－114.

[22] 黄真，赵永生，赵铁石. 高等空间机构学[M]. 北京：高等教育出版社，2006：277－283.

[23] 陈学东，孙翊，贾文川. 多足步行机器人运动规划与控制[M]. 武汉：华中科技大学出版社，2006：122－135.

[24] Sakakibara Y, Kan K, Hosoda Y, et al. Foot trajectory for a quadruped walking machine[C]//IEEE International Workshop on Intelligent Robots and Systems, Ibaraki, 1990: 315－322.

[25] Roy S S, Pratihar D K. Dynamic modeling, stability and energy consumption analysis of a realistic six-legged walking robot[J]. Robotics and Computer-integrated Manufacturing, 2013, 29: 400－416.

[26] McGhee R B, Frank A A. On the stability properties of quadruped creeping gaits[J]. Mathematical Biosciences, 2002, 3: 331－351.

[27] 李满宏，张建华，张明路. 新型仿生六足机器人自由步态中足端轨迹规划[J]. 中国机械工程，2014，25(6)：821－825. Li Manhong, Zhang Jianhua, Zhang Minglu. Foot trajectory planning for a hexapod biomimetic robot using free gait [J]. China Mechanical Engineering, 2014, 25(6): 821－825. (in Chinese with English abstract)

[28] Yoneda K, Hirose S. Tumble stability criterion of integrated locomotion and manipulation[C]// IEEE International Conference on Intelligent Robots and Systems, Osaka, Japan, 1996, 2: 870－876.

[29] 谢惠祥，罗自荣，尚建忠. 四足机器人对角小跑动态控制[J]. 国防科技大学学报，2014，36(4)：146－151.

Xie Huixiang, Luo Zirong, Shang Jianzhong. Dynamic control for quadrupedal trotting locomotion[J]. Journal of National University of Defense Technology, 2014, 36(4): 146－151. (in Chinese with English abstract)

[30] 张国腾，荣学文，李贻斌，等. 基于虚拟模型的四足机器人对角小跑步态控制方法[J]. 机器人，2016，38(1)：64－74. Zhang Guoteng, Rong Xuewen, Li Yibin, et al. Control of the quadrupedal trotting based on virtual model[J]. Robot, 2016, 38(1): 64－74. (in Chinese with English abstract)

[31] 王立鹏，王军政，汪首坤，等. 基于足端轨迹规划算法的液压四足机器人步态控制策略[J]. 机械工程学报，2013，49(1)：39－44. Wang Lipeng, Wang Junzheng, Wang Shoukun, et al. Strategy of foot trajectory generation for hydraulic quadruped robots gait planning[J]. Journal of Mechanical Engineering, 2013, 49(1): 39－44. (in Chinese with English abstract)

牛建业，王洪波，史洪敏，李 东，李姗姗，吴少振. 变自由度轮足复合机器人轨迹规划验证及步态研究[J]. 农业工程学报，2017，33(23)：38－47. doi：10.11975/j.issn.1002-6819.2017.23.006 http://www.tcsae.org

Niu Jianye, Wang Hongbo, Shi Hongmin, Li Dong, Li Shanshan, Wu Shaozhen. Trajectory planning verification and gait analysis of wheel-legged hybrid robot with variable degree of freedom[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(23): 38－47. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.23.006 http://www.tcsae.org

Trajectory planning verification and gait analysis of wheel-legged hybrid robot with variable degree of freedom

Niu Jianye1,2, Wang Hongbo1,2※, Shi Hongmin1, Li Dong1, Li Shanshan1, Wu Shaozhen1

(1.066004,; 2.066004,)

With the continuous promotion of agricultural modernization in China, new requirements for agricultural robots are put forward. The agricultural robots are developing in the direction of automatic walking and unmanned operation, and the working environment is extended from structured environment to unstructured environment. In the future, the agricultural robots should be able to change DOF (degree of freedom) through mechanical structure changes and carry different end effectors to adapt to different types of crops, which can achieve one machine multipurpose and improve the utilization rate. In order to adapt to the new requirements of modern agriculture for robots, according to the principle of bionics, this paper presents a novel quadruped robot with 3-DOF leg mechanism based on the serial-parallel and wheel-legged mechanism, which consists of 2-universal joint-prismatic joint-spherical joint plus universal joint, and revolute joint ((2-UPS+U) &R). Firstly, based on the principle of bionics, the leg mechanism and the whole structure of the robot are developed. The walking of human and animal is realized by the contraction and relaxation of the skeletal muscle to drive the bone, and through the analysis of the distribution of muscle structure, the mechanism uses 2 electric push rods to mimic the muscle distribution of the leg to drive the swing of the robot’s upper leg in 2 directions. The mechanism has the combining advantages of series mechanism and parallel mechanism. It overcomes small work space and can achieve high precision and strong bearing capacity. The robot not only can walk in four-legged mode, but also can curl up the lower leg and become the wheeled mode to achieve rapid movement. According to the analysis of the robots with high speed and heavy load at home and abroad, the desired maximum load of the robot studied is 200 kg, the maximum speed in the legged mode is 1 m/s, and the maximum speed in the wheeled mode is 5 m/s. According to the design objective, the parameters of each part are optimized. Then the forward and inverse kinematics analysis of position for swing leg is carried out. Secondly, according to the general terrain and obstacle terrain in agriculture, the constraints for trajectory planning are put forward. Then the general trajectory planning functions of the robot’s foot-end in forward step and side step are obtained, and the obstacle negotiating trajectory of the robot foot-end is planned by spline interpolation curve, which provides the basis for robot gait planning. The obstacle trajectory planning is simulated by using the ADAMS software, results showed that the lifting height is 98.2 mm with error of 1.8 mm, and the step length is 101.3 mm with error of 1.3 mm, witch show that the robot can overcome small obstacles, and the trajectory planning is correct. The velocity and acceleration of the leg mechanism are continuous without distortion points, and the leg’s jerking movement and concussion are eliminated. All the results above show that the foot-end can achieve soft landing, and the kinematics and foot-end trajectory planning are correct. Thirdly, according to the requirement of robot gait planning, the static stability criterion and the ZMP (Zero Moment Point) theory of dynamic stability criterion are analyzed. Under the premise of ensuring the stability, the diagonal trot gait planning of robot is completed, and the fast walking of the robot is achieved. Based on the diagonal trot gait planning of the robot, the simulation is carried out. The simulation results show that the robot moves steadily and fast, with the height of the robot’s center of gravity changing only about 0.9 mm, and the gait planning is correct. Finally, the trajectory planning experiment of the robot’s single leg prototype is carried out. The leg prototype can move according to the given trajectory, and the feasibility of the mechanism design is verified. The trajectory tracking experiment shows that there are some errors between the theoretical trajectory and the actual trajectory. The maximum error of y-axis is 2.5 mm and the maximum error of z-axis is 5.3 mm, but the errors are less than 10 mm, within the allowable range of error. The errors mainly come from the manufacturing errors and assembly errors. In the future, the turn gait, pivot steering gait and climbing stair gait will be studied. The research on stability analysis and gait planning will provide a theoretical basis for establishing control system of the quadruped robot.

robots; trajectories; verification; wheel-legged hybrid robot; variable degree of freedom; series-parallel mechanism; gait planning

10.11975/j.issn.1002-6819.2017.23.006

TP242.6

A

1002-6819(2017)-23-0038-10

2017-06-04

2017-11-02

欧盟地平线2020项目H2020-MSCA-RISE-2016: Smart Robot for Fire-fighting（No.：734875）；欧盟第七框架计划项目FP7-PEOPLE-2012-IRSES：Real-time adaptive networked control of rescue robots (No.：318902)；燕山大学机械工程学院协同创新项目（JX2014-01）

牛建业，男，河北保定人，博士生，主要从事并联机器人理论与应用方面的研究。Email：jyniu@ysu.edu.cn

王洪波，男，河北邢台人，教授、博士研究生导师，主要从事康复机器人和微创手术机器人方面的研究。Email：hongbo_w@ysu.edu.cn