基于边界相切拟合的轴对称工件缺陷重构方法*

陈友兴，刘蔺慧，吴其洲，李海洋，王召巴

（中北大学信息与通信工程学院，太原 030051）

基于边界相切拟合的轴对称工件缺陷重构方法*

陈友兴，刘蔺慧，吴其洲，李海洋，王召巴

（中北大学信息与通信工程学院，太原 030051）

针对轴对称工件超声检测缺陷重构问题，通过分析传统基于传播时间反演方法的不足和误差产生的原因，提出了一种基于边界相切拟合的缺陷重构方法，并针对实际检测缺陷的类型，采用圆和椭圆作为模型对缺陷进行重构。从重构结果上看，当检测实心体工件时，圆形缺陷的圆拟合重构误差不大于0.1 mm，圆形缺陷的椭圆拟合重构误差小于0.4 mm，椭圆形缺陷的椭圆拟合重构误差小于0.3 mm，空心体工件由于检测方式不同，误差会比实心体大一些。

超声检测，缺陷重构，边界相切，椭圆拟合，传播时间

0 引言

轴对称工件在生产过程和使用过程中常常会带来缺陷，影响着产品的正常和安全使用，因此，需要对产品进行缺陷检测。目前，一般的方法是通过旋转工件和移动超声探头来实现工件的整体扫描，并完成重构［1］，其中，圆截面的缺陷重构技术是轴对称工件缺陷检测的关键。

kirchhoff近似、born近似和k-wave伪谱法是目前较为常用的适用于单一截面的逆时反演技术［3-5］，但这些方法对检测回波数据要求很高，且最终的结果也只能得到最终的声场反演成像效果，大大地影响了其实用性。

本文针对轴对称体工件，采用文献［1］的检测方式，通过分析传统基于传播时间缺陷边界确定方法的不足及原因，提出了一种基于边界相切拟合的重构方法。为了验证本文方法的有效性和准确性，还用Comsol Multiphysics软件［6］模拟理想缺陷，并进行重构。

1 基于传播时间缺陷边界确定方法的局限性

本文的检测方式与文献［1］相同。图1（a）是针对一带有圆孔缺陷的铝圆柱体进行某一截面扫查的超声B扫描图，铝圆柱体外径为100 mm，在检测截面上以中心点为原点，在（25，0）和（0，-25）处各有一个直径Φ4 mm的圆孔；图1（b）是提取出来的外表面回波与缺陷回波的传播时间差Δt。

根据传统基于传播时间缺陷边界确定方法，利用图1（b）即可以确定出超声波在缺陷表面的反射点，从而确定出缺陷的边界。图2（a）是实心体缺陷得到的结果，从结果中看，缺陷边界明显存在误差，其根源在于超声波在传播时是以一定扩散角传播的，在这个扩散角内遇到缺陷都会返回缺陷回波，因此，从单一缺陷回波中确定边界点是不科学的。

如图2（b）所示，超声波由探头A'处以一定的半扩散角∠M1AM2=∠M3AM2=α1发射出去，经耦合界面到达缺陷表面反射，A点是M1N1、M2N2的交点，即超声的镜像发射点，那么∠M1A'M2=∠M3A'M2=α2为超声波在检测介质中传播的扩散角，根据Snell定理，

式（1）中，c1和c2分别为耦合介质（水）和检测介质（铝）的纵波声速。根据式（1）可知，由于铝的声速是水的4倍左右，那么即使超声初始发射半扩散角α1很小，那么弧线N1N3会随着传播距离的增加而增加，且不可忽略。这里假设α1很小，那么有AM1=AM2，A'M1=A'M2，检测工件表面的圆弧 M1M3可以近似为直线。从图2（b）可知，在已知Δt的情况下，可以知道缺陷的边界点一定在以A为圆心，以d=AM2+l为半径的圆上，AM2可以根据声速和探头与工件表面的距离A'M2来求得。

2 基于边界相切的重构原理

从图2（b）的分析可知，当有多个探测点时，可以根据每个探测点确定的圆弧重构出缺陷的边界。根据缺陷的特征信息（包括探测点位置和距离d），可以画出所有的圆弧信息（本文称作波前圆弧）。用图1的数据可以得到如图3的波前圆弧。从图3中可以很直观地看出缺陷的区域，因此，只要能够拟合出与这些弧线相切的缺陷边界那么就完成了缺陷重构。圆、椭圆可以作为实际中大部分缺陷的重构模型，下面介绍其重构原理。

2.1 圆形缺陷重构方法

假设一缺陷可以用圆形模型来进行重构，该模型所需要确定的参数包括圆心 O（x0，y0）和半径 r。如图4所示，图中A1～A3为具有缺陷信息的探测点的镜像发射点，d1～d3为包含缺陷信息的距离，Cj为以Aj（xj，yj）为圆心，dj为半径的圆弧（j=1，2，3），根据两圆相切的原理，可以列出方程组：

理论上可以通过求解方程组（2），得到x0，y0和r。实际检测中波前弧线不可能得到精确解，缺陷也不可能是精确的圆形，因此，不能通过这个方式进行求解。由于每个缺陷所对应的缺陷回波信息远远大于3个，因此，可以通过最小二乘法拟合出最佳解，拟合方程可以写成

在已知dj，xj，yj的情况下可以通过数值拟合得到圆心x0，y0和r。K越大，拟合精度越高。

2.2 椭圆形缺陷重构方法

假设一缺陷可以用椭圆形模型来进行重构，该模型所需要确定的参数包括椭圆中心O（x0，y0）、长半轴a、短半轴b和倾斜角θ。直角坐标系下的椭圆方程可以写成

也可以写成

式中，pi（i=1，2，…，5）为方程参数，式（4）和式（5）的两种形式可以互相转换。

因此，从理论上来说，只要能够找到5个及以上的缺陷数据，就能用类似于圆的拟合方法，拟合出椭圆方程。在已知圆与椭圆的情况下，可以通过数值方法求解出相切相关的参数，但在未知椭圆的情况下，期望通过已知外切圆来拟合椭圆的问题，据了解还没有直接解析求解方法。针对这一问题，本文提出了采用两圆相切近似圆与椭圆相切的方法，将椭圆的不同弧线段用不同半径的圆来近似，以此求得相应的切点，并进行椭圆拟合。

图5示出了用圆弧来近似椭圆弧的情况，如在Q1、Q2、Q3点处分别用圆弧 CC1、CC2、CC3来近似椭圆弧。从图中可以看出，当椭圆弧足够短时，具有很高的近似精度。

下面具体介绍本文的椭圆重构方法。已知有K组相邻的缺陷数据，先提取出第1～L组的数据，对应的信息有 A1～AL、d1～dL、C1～CL，采用式（3）的方法重构出圆（中心点为O1），并求出相应的切点。实际上CC1不能与所有的C1～CL都相切，因此，并不能找到真正意义上的切点。考虑到缺陷边界一定在波前圆弧Cj上，所以这里确定Cj与AjO1的交点作为波前圆弧Cj与CC1的近似切点。依次类推取第2～（L+1）组、第 3～（L+2）组、…、第（K-L+1）～K 组可以拟合出 CC1、CC2、…、CCK-L+1，并得到相应的 CCi与 Aj近似切点Bij。这样对于每个阵元Aj都会得到在Cj最少1个最多L个对应的切点，Bij的分布见式（6）。

对于在同一波前圆弧Cj上的所有近似切点Bij，取中间点作为最终的切点Bj。这样K组缺陷数据就能得到K个切点Bj（j=1～K），并由这K个切点按最小二乘法拟合出椭圆。

3 数据验证

采用第2节的算法，针对图3的数据进行缺陷重构，其结果如下页图6所示，具体参数如表1所示，表中位置为中心坐标（x0，y0），圆的尺寸用半径r表示，椭圆的尺寸用长半轴a和短半轴b表示。从图6和表1中可以看出，采用圆拟合时尺寸相当，但位置上有点偏离，椭圆拟合的结果基本上包含了理想边界和拟合圆的区域，短半轴与圆半径相当，长半轴误差较大，基本上体现了图3中总体轮廓的尺寸和方向。

表1中的位置和尺寸的偏差可能还和实际工件的制作有关，本文中理想边界的参数（位置和尺寸）是根据工件设计的尺寸得到，并不是通过准确测量最终产品的尺寸得到的，因此，实际工件的大小与理想边界还有一定的误差。为了说明本文方法重构的精度和有效性，下面采用Comsol Multiphysics软件模拟理想工件的检测过程，并按照本文的方法进行重构。Comsol Multiphysics软件是一款有限元软件，可以模拟超声波的传播过程，并获取监测点的回波信号。

表1 实际检测重构结果的参数分析（单位mm）

表2 仿真圆形缺陷重构的参数分析（单位mm）

图7是模拟直径为100 mm的一铝圆柱体的B扫描图，围绕工件表面每1°仿真一个超声回波信号，仿真时计算步长为0.1 μs，即采用频率为10 MHz，工件中存在两个直径为10 mm的圆形缺陷。从图7可以看出表征缺陷的特征与图1基本一样。图8是缺陷重构结果，表2为相应的参数。从结果中可以看出对于圆形缺陷，采用圆拟合方法进行重构的位置误差小于0.05 mm，尺寸误差不大于0.1 mm；采用椭圆拟合方法进行重构的位置误差小于0.2 mm，尺寸误差小于0.4 mm。

图9是对椭圆形缺陷进行检测仿真得到的缺陷重构结果，其中图9（a）的工件是一直径为100 mm的铝实心圆柱体，图9（b）的工件是一外径为100mm，内径为60mm的铝空心圆柱体，阵元偏离中心5.6mm入射，折射角约为30°，其余仿真条件与图7的一样，表3是缺陷理想参数和重构参数。

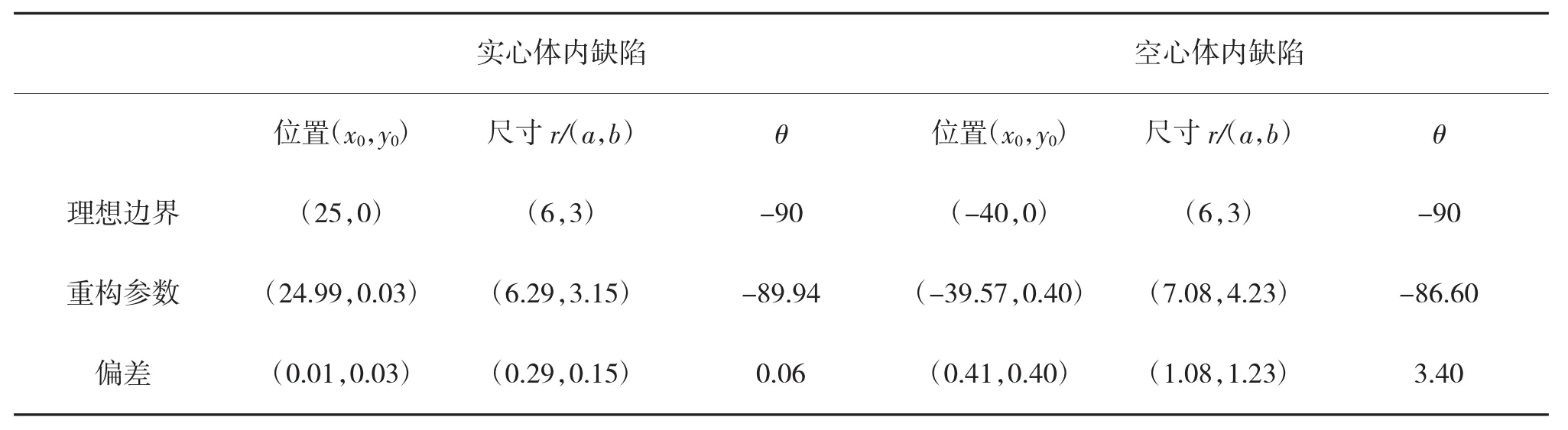
表3 仿真椭圆形缺陷重构的参数分析（单位mm°）

从表3可以看出，对于实心体来说，椭圆形缺陷重构的位置误差小于0.05mm，尺寸误差小于0.3mm，方向误差小于1°；对空心体来说，所有误差都相对大一些，主要原因是空心体检测时采用偏离中心发射和接收，在工件和耦合界面表面存在折射角问题，缺陷反射回波信号的成份也更复杂，因此，可以通过更加准确地提取缺陷的时间特征，以及入射点的校正来提高重构精度，这将是本项目下一步的研究内容。

4 结论

本文针对轴对称工件超声检测缺陷重构问题，通过分析传统基于传播时间反演方法的不足和误差产生的原因，提出了一种基于相切拟合的缺陷重构方法，针对实际检测常见缺陷的类型，采用圆和椭圆作为模型对缺陷进行重构，结论如下：

（1）本文的方法是在传统基于声线分析的传播时间反演方法的基础上，考虑了超声传播的扩散角因素，提高了反演精度；

（2）对于实心圆柱体，垂直入射检测时由于声束在圆形界面入射和透射都呈对称的，因此，重构精度较高；而偏离中心入射，存在入射点处不对称、具有较大折射角问题，增大了重构误差；

（3）从重构结果上看，圆形缺陷用圆拟合比椭圆拟合更加准确有效，因此，在实际拟合中重构模型的选择也是很重要的一个环节。

［1］陈友兴，吴其洲，赵建辉，等，合金火箭弹弹体缺陷超声自动检测及信号处理 ［J］. 固体火箭技术，2013，36（5）：706-710.

［2］肖兆骞，陈友兴，任阳山，等.基于体绘制的圆柱体构件缺陷三维重构方法 ［J］. 火力与指挥控制，2015，41（3）：22-25.

［3］郑钢丰，吴斌，何存富.用改进的Kirchhoff方法重构非均匀介质中缺陷形状 ［J］. 压电与声光，2012，34（1）：118-120.

［4］顾雯琪.超声检测柱状体内缺陷的三维反演方法研究［D］.太原：中北大学，2015.

［5］李雅.基于声场模型的回旋体内部缺陷重构方法研究［D］.太原：中北大学，2016.

［6］WANG M，YUAN W，HALE A.Three-dimensional simulation of ultrasound-induced microalgal cell disruption［J］.Applied Biochemistry and Biotechnology，2016，178（6）：1184-1195.

Reconstruction for Flaw in Axisymmetric Workpiece Based on Boundary Tangent Principle and Fitting Technology

CHEN You-xing，LIU Lin-hui，WU Qi-zhou，LI Hai-yang，WANG Zhao-ba
（School of Information and Communication Engineering，North University of China，Taiyuan 030051，China）

Ultrasonic is used to detect the flaw in the axisymmetric workpiece.This paper analyzes the reason for the shortage and the error of the tradition reconstruction method based on travel time，and proposes an improved reconstruction method based on boundary tangent principle and fitting technology.The circle model and ellipse model are used respectively.The results show that for the workpiece with solid body，the errors are not more than 0.1 mm when circle model used for circle flaw，and the errors are less than 0.4 mm when ellipse model used for circle flaw，and the errors are less 0.3mm when ellipse model used for ellipse flaw.The results also show that the workpiece with hollow body has bigger error than that with solid body，because ultrasound is in normal incidence mode for the former，and in off-center incidence mode for the latter.

ultrasonic testing，flaw reconstruction，boundary tangent，ellipse fitting，travel time

TB52

A

10.3969/j.issn.1002-0640.2017.11.27

1002-0640（2017）11-0126-05

2016-09-17

2016-10-27

国家自然科学基金（61201412，11604304）；山西省青年学术带头人计划基金；山西省自然科学基金（2012021011-5）；山西省高等学校科技创新基金资助项目（201657）

陈友兴（1978- ），男，福建福安人，博士，副教授。研究方向：超声检测及信号处理。