基于动态贝叶斯网络的复杂网络抗毁性分析*

胡 鑫 ，王 刚 ，2，马润年

（1.空军工程大学信息与导航学院，西安 710077；2.空军工程大学防空反导学院，西安 710051）

基于动态贝叶斯网络的复杂网络抗毁性分析*

胡 鑫1，王 刚1，2，马润年1

（1.空军工程大学信息与导航学院，西安 710077；2.空军工程大学防空反导学院，西安 710051）

复杂网络抗毁性是复杂网络在节点或边遇敌攻击后能继续维持基本功能的能力，是衡量军事信息网络鲁棒性和敏捷性的重要指标。针对复杂网络及对作战体系支撑能力的多指标、复杂化和动态演绎特点，在静态分析方法基础上，提出基于动态贝叶斯网络的抗毁性分析方法。建立了复杂网络抗毁性指标体系。构建了基于动态贝叶斯网络的复杂网络抗毁性评估模型，提出确定评估模型参数的方法。仿真验证了方法的可行性和有效性。

动态贝叶斯网络，复杂网络，抗毁性

0 引言

复杂网络抗毁性是指复杂网络在节点或边遭受攻击后继续维持基本功能的能力，是战场复杂网络性能的重要度量指标。通信领域的复杂网络抗毁性通常仅考虑网络拓扑结构的可靠性［1］，军事领域的复杂网络抗毁性则指己方网络在遭受敌火力打击情况下，在规定时间内完成预定任务的能力［2］。一般意义上，复杂网络抗毁性指复杂网络在其节点（或边）失效后，能够继续维持基本性能的能力［3］。

关于复杂网络抗毁性研究，主要集中在复杂网络抗毁性的静态拓扑结构分析。如Albert和Barabasi等人提出了不同的网络拓扑结构应对节点失效的鲁棒性问题［4］。文献［5］引入自然连通度指标来分析衡量复杂网络的抗毁性；文献［6］结合无标度网络和随机网络模型、分析了网络拓扑结构对复杂网络抗毁性的影响；文献［7］提出增加小度节点间连接边的方法来分析复杂网络抗毁性。复杂网络抗毁性的静态分析，注重复杂网络物理拓扑的抗毁性，但忽略了在时序变化情况下的复杂网络效能，缺乏对复杂背景下网络的抗毁性预测。围绕抗毁性动态分析；文献［8］从初始负载定义、负载分配原则和负载容量出发，分析了级联故障模型；文献［9］针对无尺度网络仿真研究了在网络最大负载节点失效情况下，网络的聚集系数、平均度和幂律指数等指标与级联抗毁性的相关关系。总体来讲，现有的动态分析，主要针对复杂网络级联抗毁性，考虑在时序变化情况下网络构建成本和级联抗毁性的双重优化。由于各网络节点（或边）之间的级联关系，如果网络中有节点（或边）失效则会导致网络中其他节点（或边）失效，最终会导致整个网络的崩溃［10］，客观上制约了级联抗毁性分析。

基于此，本文提出了基于动态贝叶斯网络的复杂网络抗毁性分析。动态贝叶斯网络反映相邻时间片之间的相互依赖关系，不仅能够准确、清晰地刻画复杂网络抗毁性随时序变化的情况，还能对复杂网络节点（或边）的变化及复杂网络抗毁性进行连续的感知和动态分析。

1 动态贝叶斯网络理论与方法

1.1 动态贝叶斯网络理论

动态贝叶斯网络是贝叶斯网络在时序上的扩展，动态是指贝叶斯网络中节点的值是动态变化的［11］。在动态贝叶斯网络中，时间片通过弧与相邻时间片连接，反映了与相邻时间片之间的相互依赖关系，它不仅具有静态贝叶斯网络的功能特性，还能在时序范围内充分体现复杂网络节点抗毁性对整个网络结构的影响。将DBN表示为，其中先验网络B0表示起始贝叶斯网络，转换网络表示两个或两个以上时间片的贝叶斯网络。用条件概率表示前一时刻概率已知情况下，当前状态发生的概率。

1.2 动态贝叶斯网络方法

隐形马尔科夫模型（Hidden Markov Model，HMM）［11］是动态贝叶斯网络常用的方法。HMM在每个时序内产生一个预测值和一个观测值，HMM状态变化图如图1所示。

其中，HMM的推理算法如下：

由于 Xt=i，d 分离了 yt+1：T和 y1：t，有：，考虑到y1：t观测值是确定的，因此

2 复杂网络抗毁性指标

复杂网络抗毁性指标的选取，应遵循独立、可测和层次性的体系构建原则。考虑网络攻防特点，复杂网络抗毁性指标的选取应重点考虑3个问题：是否成功实现预定目标的效果，抵御攻击所付出的代价以及网络节点（或边）受到攻击后依然能维持复杂网络基本性能的能力。以下将指标体系的一级指标分为抗毁性收益、抗毁性损耗和抗毁性顽存。参考复杂网络静态抗毁性［12］和复杂网络动态级联抗毁性的指标测度［13］，又在一级指标下划分出二级指标，其中，抗毁性收益划分为网络凝聚度、节点重要性和聚集系数；抗毁性损耗分为失效节点数、初始负载和相对增加成本；抗毁性顽存分划分为网络易毁性和网络恢复性。具体如下页图2所示。

2.1 抗毁性收益

抗毁性收益是指我方网络在受到攻击后，网络能够实现预定目标所获得的效果。

网络凝聚度 ρ（G）定义为［14］：

其中，q（i）为节点i的强度，li为节点i相邻节点数，dij为节点i与节点j之间的最短路径。

节点重要性 IMC（i）定义为［14］：

其中，G'（i）表示将网络节点i收缩后所得的网络。

聚集系数 Ci定义为［5］：

其中，Ei为节点i相邻节点之间实际连边数量，ki为节点i的相邻节点数量。

2.2 抗毁性损耗

抗毁性损耗是指我方网络抵御敌方网络攻击所付出的代价。

失效节点数CF定义为［15］：

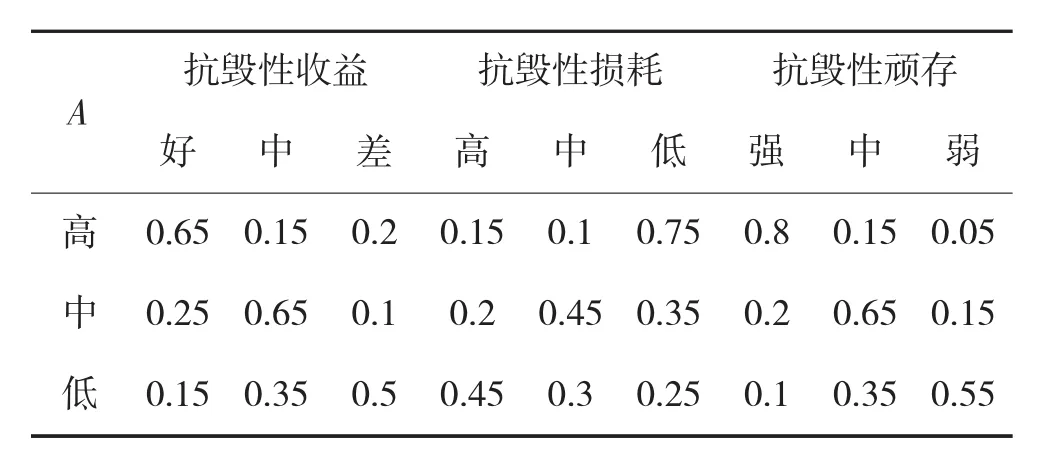
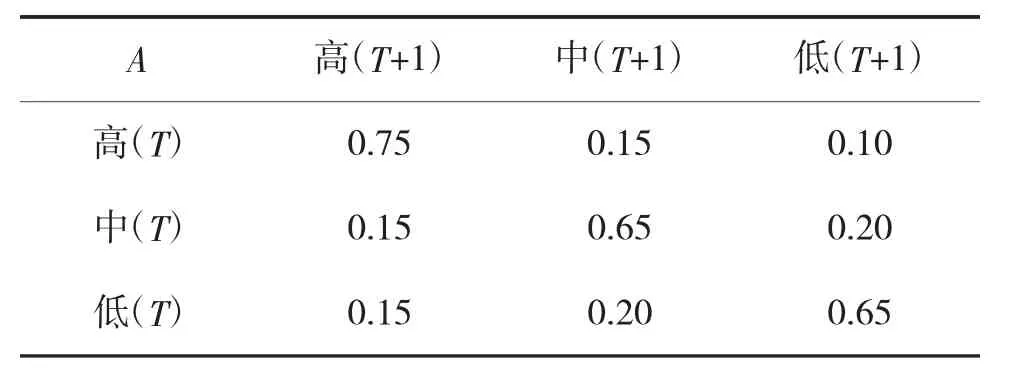
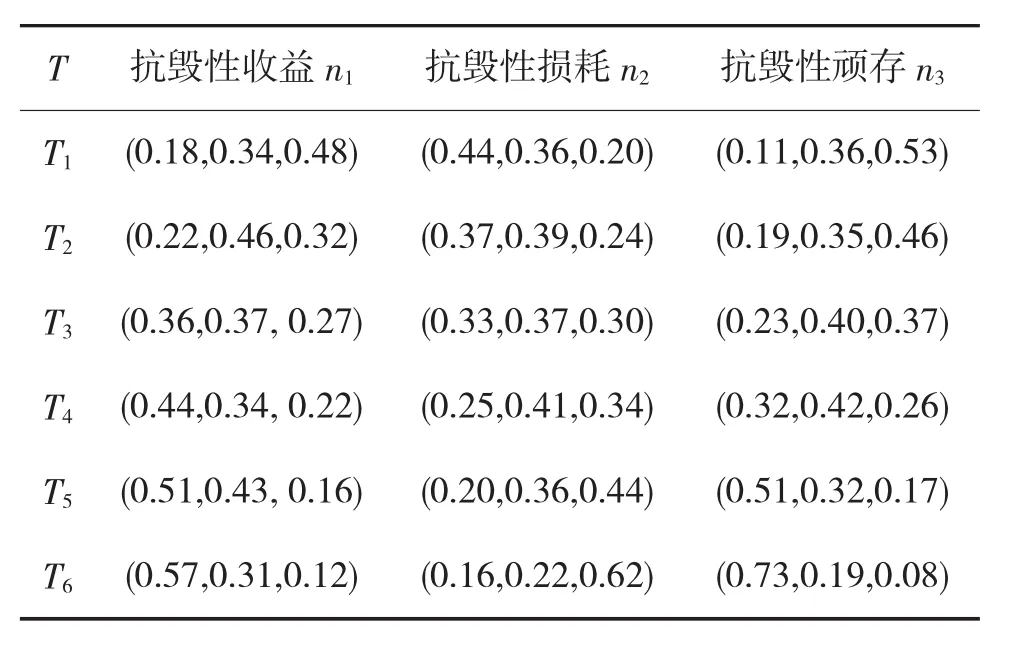
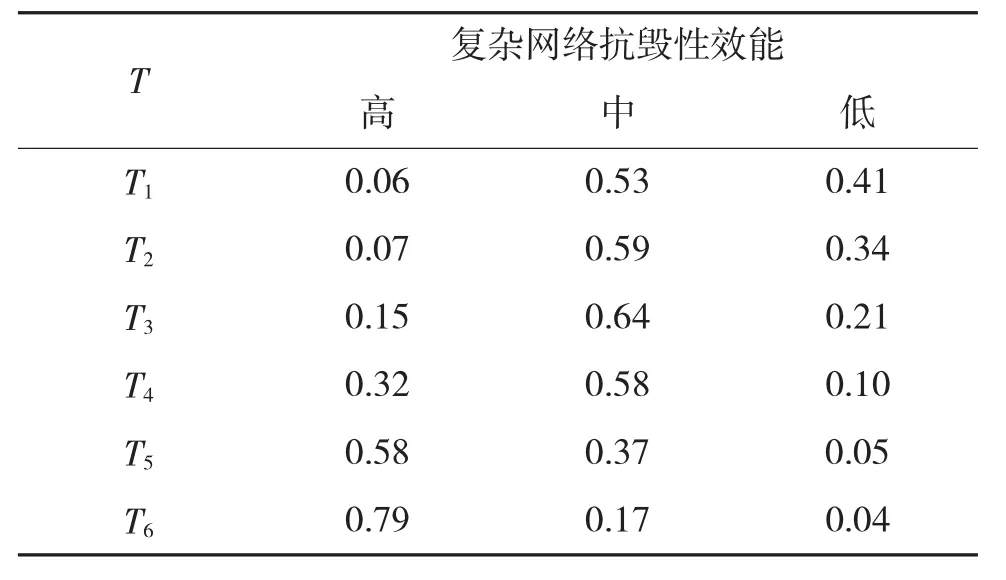
其中，CFn（0

初始负载 Li定义为［8］：

其中，ki为节点度，hi为节点的通信层级，H为网络总通信层级，γ和θ为负载参数。

相对增加成本I定义为［15］：

其中，ΔCi和Li分别为网络中节点的空闲容量和初始负载。

2.3 抗毁性顽存

抗毁性顽存是指我方网络节点抵域敌网络攻击的能力。

网络易毁性定义为［16］：

网络恢复性定义为［16］：

3 基于动态贝叶斯网络的复杂网络抗毁性模型

3.1 动态贝叶斯网络分析模型

复杂网络抗毁性效能分析指标各要素之间，既有层级关系，还包括指标要素之间的相互影响和相互联系。分析复杂网络抗毁性效能，可将抗毁性效能视为目标节点，底层的影响因素视为网络节点［17］，按照控制层、网络层两个层次，通过上述分析，构建基于动态贝叶斯网络的复杂网络抗毁性效能分析模型，如图3所示。并对准则层指标进行模糊取值，如表1如示。

3.2 确定评估模型参数

复杂网络抗毁性效能分析的模型参数主要有：一是起始网络节点的条件概率，反映了网络中关联节点之间的因果关系，在实际分析过程中，该值可由专家根据经验知识给定；二是网络状态转移概率，反映了各时间片之间网络节点状态改变的概率，在实际分析过程中，该参数值可由专家对以往的历史数据进行分析，再结合经验知识加以给定。由于受到专家经验知识的影响，模型的参数值在一定程度上存在主观性，因此，在实际过程中，可通过取多组数据，并将这些数据导入模型中进行多次调试，得到结果后对模型参数进行适当的调整，从而提高可信度。

由于缺少充足的事例充当模型的统计样本，以下评估模型的参数值，是在该领域相关资料的基础上，综合专家意见，并进行合理假设给出的。节点准则层指标的条件概率分布如表2所示，节点状态转移概率表如表3所示。

表2 节点准则层条件概率表

表3 节点状态转移概率表

4 仿真算例

由于动态贝叶斯网络推理建立在观测信息基础之上，因此，分析网络抗毁性效能需要观测统计节点在时间片内的概率值，并将观测值输入动态贝叶斯网络模型，触发网络推理，最终得出根节点（即复杂网络抗毁性效能）的状态概率，完成评估。

表4 节点准则层观测概率值

在网络攻击行动开始后，分别对抗毁性收益、抗毁性损耗和抗毁性顽存3项指标分别进行6次观察统计，如表4所示。由于预先获取情报有限，本文假设网络抗毁性优先等级相同，即高、中、低的概率分别为0.33、0.34、0.33。

表5 复杂网络抗毁性效能概率表

由表4的观测数据可知，随着时间的推移，抗毁性收益好、抗毁性损耗低、抗毁性顽存强的概率都有一定的提升，相应的抗毁性效能高的概率也随之增加，表明复杂网络抵御不确定攻击的强度随着时间的推移越来越强。将上述观测数据输入到动态贝叶斯网络模型中，对模型进行推理，得到各观测时间点复杂网络抗毁性效能概率，如表5所示，复杂网络抗毁性效能概率分布图，如下页图4所示。

仿真结果分析：复杂网络抗毁性效能与抗毁性收益、抗毁性损耗、抗毁性顽存均呈正相关关系。由图4可以看出，抗毁性效能高的概率在起始时刻明显低于抗毁性效能低的概率，但随着时间推移，在某一时刻（图中T3时刻）附近，抗毁性效能高的概率将超过抗毁性效能低的概率，且两者之间的差距随时间的增长越来越大，且抗毁性效能高的概率增长速度越来越快，并在一定时刻达到稳定状态。仿真结果表明运用基于动态贝叶斯网络的复杂网络抗毁性分析方法，能够准确清晰地对各时间节点复杂网络抗毁性进行持续感知和动态分析。

5 结论

复杂网络抗毁性效能分析，是促进网络化作战理论发展、构建良好的军事信息网络鲁棒性和敏捷性的重要手段。本文结合动态贝叶斯网络对复杂网络抗毁性进行动态分析，通过分析构建网络抗毁性评估指标体系和评估模型，仿真验证了模型的可行性和有效性。该方法结合专家经验知识，实现了对各时间节点的复杂网络抗毁性的持续感知和动态分析，同时，也为复杂网络在抵御敌方网络攻击作战过程中提供了更加自主、科学和可控的决策手段。

［1］刘啸林.网络抗毁性研究介绍［J］.计算机应用与软件，2007，24（6）：135-136.

［2］田旭光，朱元昌，邸彦强.指挥控制系统网络动态抗毁性［J］.火力与指挥控制，2012，37（6）：88-91.

［3］马润年，文刚，蔺根茂.链路赋权军事通信网的抗毁性评估［J］.电光与控制，2013，20（10）：11-13.

［4］ALBERT R，JEONG H，BARABASI A L.Error and attack tolerance of complex networks［J］.Nature，2000 ，406（6794）：378-382.

［5］王班，马润年，王刚.基于自然连通度的复杂网络抗毁性研究［J］.计算机仿真，2015，32（8）：315-318.

［6］DAVID S A，MARK E T.NEC2 Effectiveness and agility：analysis methodology，metrics，and experimental results［R］.Alexandria：Institute for Defense Analysis.2012.01.

［7］ZHUO Y，PENG Y F，LONG K P.Improving robustness of complex communication networks by allocating redundancy links［C］//Communications and Photonics Conference and Exhibition（ACP），2009：1-2.

［8］段李东，吴俊，邓宏钟.基于可调负载重分配的复杂网络抗毁性级联失效模型［J］.系统工程理论与实践，2013，33（1）:203-208.

［9］彭兴钊，姚宏，张志浩.基于节点蓄意攻击的无尺度网络级联抗毁性 ［J］. 系统工程与电子技术，2013，35（9）:1978-1978.

［10］MOTTER A E，LAI Y C.Cascade-based attacks on complex networks［J］.Phys.Rev.E，2002，66（8）:065102.

［11］史建国，高晓光.动态贝叶斯网络及其在自主智能作战中的应用［M］.北京：兵器工业出版社，2008.

［12］郭世泽，陆哲明.复杂网络基础理论［M］.北京:科学出版社，2012.

［13］王甲生，吴晓平，陈永强.加权无标度网络级联抗毁性研究［J］.复杂系统与复杂性科学，2013，10（2）:13-19.

［14］朱涛，张水平，郭戎潇.改进的加权复杂网络节点重要度评估的收缩方法［J］.系统工程与电子技术，2009，31（8）:1902-1905.

［15］LI P，WANG B H，SUN H.A limited resource model of fault-tolerant capability against cascading failure of complex network［J］.Eur.Phys.J.B，2008，62（1）:101-104.

［16］LATORA V，ARCHIORI M.Vulnerability and protection of infrastructure networks［R］.Phys.Rev.E，2015，71:015103.

［17］贺平，罗小明.基于动态贝叶斯网络的电子对抗演练效果评估研究［J］.装备学院学报，2014，25（3）:120-124.

［18］张肖，戴明强，邵帅.舰艇装备保障网络的抗毁性分析［J］.兵器装备工程学报，2016，37（1）:97-101.

Complex Network Invulnerability Based on Dynamic Bayesian Network

HU Xin1，WANG Gang1，2，MA Run-nian1
（1.School of Information and Navigation，Air Force Engineering University，Xi’an 710077，China；2.School of Air Defense and Anti Missile，Air Force Engineering University，Xi’an 710051，China）

Complex network invulnerability is the ability to maintain the basic function of the complex network in case of node or edge attack，and it’s the important factor to measure the robustness and agility of information network in military area.In view of the complex network performance and the multi index，the complexity and the dynamic deductive characteristic to the support ability of the combat system，a innovation method of Dynamic Bayesian Network（DBN）invulnerability are proposed，compared with the method of static analysis.In detail，the complex network invulnerability index system is first established，and the model is presented based on DBN，as well as method to determine the parameters of the evaluation model.Finally，simulation results show that the method is available and effective.

Dynamic Bayesian Network（DBN），complex network，invulnerability

TN91

A

10.3969/j.issn.1002-0640.2017.11.02

1002-0640（2017）11-0005-05

2016-09-17

2016-11-27

国家自然科学基金（61573017）；国家社科基金资助项目（15BGJ007）

胡 鑫（1993- ），男，湖南湘西人，硕士研究生。研究方向：复杂系统建模。