导弹弹头的单脉冲雷达检测概率计算及性能评估
2017-12-18秦建强孔祥玉胡绍林马红光
秦建强, 孔祥玉, 胡绍林, 马红光
(1.火箭军工程大学,西安 710025; 2.西安卫星测控中心故障诊断实验室,西安 710043;3.北京理工大学珠海学院航空学院,广东 珠海 519088)
导弹弹头的单脉冲雷达检测概率计算及性能评估
秦建强1, 孔祥玉1, 胡绍林2, 马红光3
(1.火箭军工程大学,西安 710025; 2.西安卫星测控中心故障诊断实验室,西安 710043;3.北京理工大学珠海学院航空学院,广东 珠海 519088)
为了提高导弹在攻击过程中的生存概率,需要合理地进行弹道设计。以锥球体作为弹头模型,基于单脉冲体制雷达,运用电磁计算软件计算弹头的雷达横截面(RCS)值,并对弹头在不同射面角和不同垂直高度下的被检测概率进行了计算。结果表明,有两个区域的检测概率较高,分别是射面角为0°~90°、弹头垂直高度为20~60 km以及射面角为270°~360°、弹头垂直高度为20~60 km的区域。射面角为90°~270°时,弹头的检测概率一直处于较低的水平,可以通过合理选择导弹的射面角来改变雷达视角,从而使弹头的被检测概率处于一个较低水平。
导弹; 生存概率; 弹道设计; RCS; 检测概率; 雷达视角
0 引言
导弹对地面军事目标进行攻击时,敌方被攻击区域的反导雷达对于导弹的突防是个重要威胁。当具有特定外形和覆盖涂层的弹头进入反导雷达的责任区域内,雷达会根据每一时刻弹头的姿态、空间位置、雷达视角做出反应,首先检测该弹头,对其运动状态进行计算,弹道计算、轨迹预测、跟踪、与火控雷达分享数据、指引反导导弹对我方弹头进行摧毁,从而实现防御反导的目的。
近年来,美国以及世界上许多国家正逐步在其领土、战区及要害目标附近布置频段多元、功能各异、性能各异的警戒雷达或预警雷达,组成战区甚至国土导弹防御系统[1],给导弹在攻击时的生存带来严重威胁。为了提高我方导弹武器生存概率,从生产过程中的导弹外形设计[2]、外壳隐身涂层[3],到导弹在使用时的弹道设计规划[4]、发射时机等全流程都要充分考虑弹头的突防性能[5]。
目前的文献大都从导弹目标的RCS是一个常数这个假设出发[6-7],进行雷达目标检测概率计算与分析。而本文从不同视角得到的目标RCS也不同这个角度出发,以锥球体作为弹头模型,基于单脉冲体制雷达,运用电磁计算软件计算弹头的RCS值,对导弹从不同方向来袭时、不同垂直高度下的被检测概率进行了计算,研究如何通过选择射面角来达到降低敌雷达检测概率,提升对敌打击效果的目的。本文有针对性地对敌方反导雷达性能进行分析,对我方导弹弹道优化、突防策略调整具有重要的参考价值。
1 雷达检测模型及雷达性能
1.1 单部单脉冲体制雷达检测模型
根据雷达方程[8]可知,在距离雷达R处散射截面积为σ的目标的信噪比为[9]
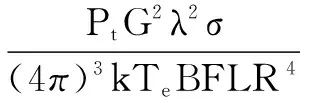
(1)
式中:Pt为发射机峰值功率;G为天线增益;λ为电磁波信号波长;σ为目标的雷达散射截面积;k为玻尔兹曼常数;Te为有效噪声绝对温度;B为接收机带宽;F为接收机噪声系数;L为雷达系统损耗;R为目标距离。
假设雷达接收机的输入信号由雷达回波信号和加性噪声信号组成,雷达接收机的两个正交通道噪声是互不相关的零均值低通高斯噪声,具有相同的方差ψ2。雷达信号是幅度为A的正弦波,功率即为A2/2。
当信号r(t)中有噪声、无目标时,信号服从瑞利分布;当信号r(t)中包含目标和噪声时,信号服从莱斯分布。
设定门限VT,当信号中仅有噪声出现且超过了门限电压VT的概率就是虚警概率,即
(2)
当信号中包含目标和噪声,且超过门限电压VT的概率就是检测概率,即

(3)
式中:RS,N为输入信号的信噪比;Q(a,b)为Marcum Q函数[10]。
根据式(3),在虚警概率Pfa一定时,计算得到信噪比RS,N,再用Marcum Q积分函数[11]即可计算得到距离雷达R处、雷达散射截面积为σ的目标的检测概率Pd。
1.2 雷达性能参数设置
雷达的技术指标设置如下:频宽4~6 GHz;捷变频带宽为640 MHz;发射峰值功率为1200 kW;发射天线增益为40 dB(主波束最大方向增益);中心工作波长为5.43 cm;发射损耗为2.7 dB;大气损耗为1 dB;探测距离为3~170 km。
2 系统建模与仿真
2.1 雷达、导弹与被攻击目标建模
针对地基雷达的防空功能,建立单部雷达目标检测的数学模型,如图1所示。
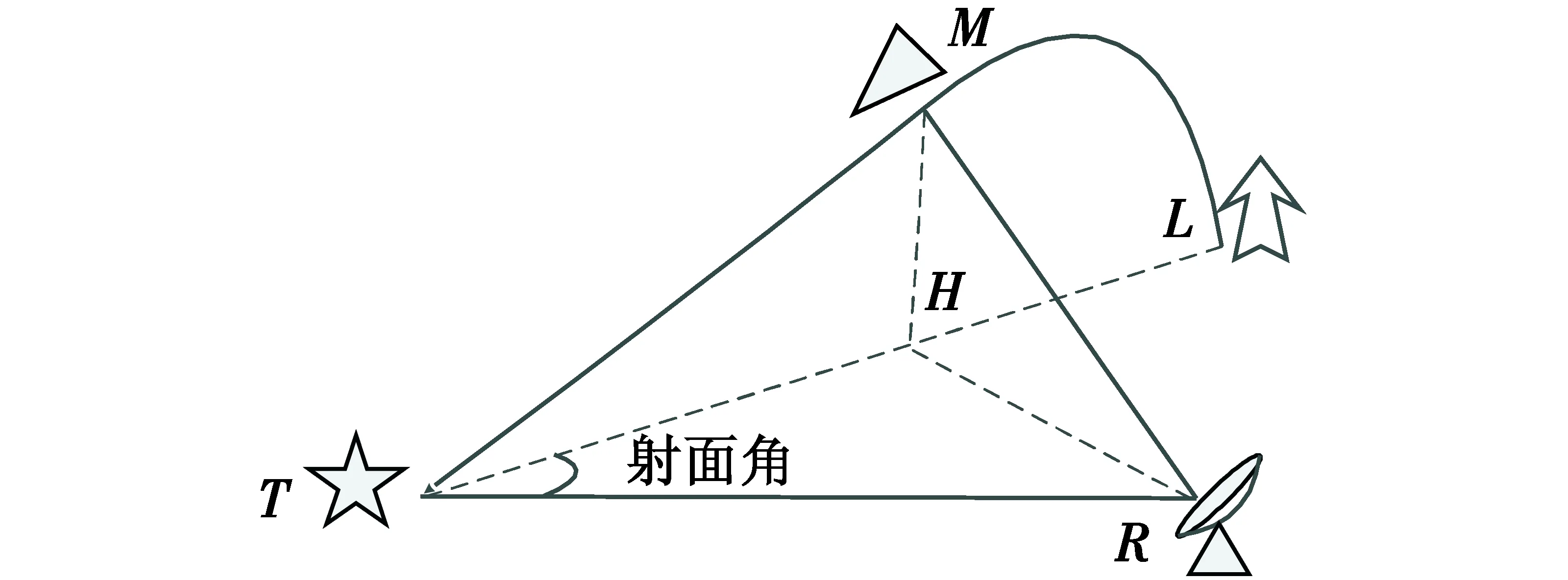
图1 单部单脉冲雷达目标检测模型Fig.1 Model of a single pulse radar for target detection
图1中:M为我方导弹;T为敌方被攻击目标;R为敌方雷达;H为导弹在大地的投影。我方导弹M以一定的攻角沿着预定弹道攻击敌方T的过程中,不仅可以实时得到自身的对地垂直高度MH,而且在弹头飞向攻击目标时会受到敌方雷达的侦测。已知,∠HTR为导弹射面与RT(即雷达与目标连线)之间的夹角,即射面角;RM的长度为雷达与导弹之间的距离;∠RMT为雷达视线与导弹飞行方向之间的夹角。
整个攻击、侦测过程可以归纳为:
1) 弹头在∠HTR为射面角的射面内,以固定攻角∠HTM飞向目标的过程中,实时得到自身的垂直高度MH;
2) 雷达在此过程中实时侦测弹头,并根据雷达与被攻击目标之间的距离RT,实时解算雷达与弹头之间的斜距RM和雷达对弹头的视角∠RMT;
3) 根据雷达性能参数和预先得到的弹头RCS值,结合2)中得到的雷达与弹头之间的斜距,首先计算出信噪比RS,N,再计算出雷达对弹头的检测概率。
2.2 弹头建模及其RCS仿真

通过比较文献中弹头的尺寸与雷达的波长(38λ×18λ×4λ=2736λ3)可知,该目标属于电大尺寸目标。利用电磁计算软件CST(试用版)的微波工作室积分求解器进行RCS计算,软件求解器设置为多层快速多极子算法(MLFMM)[13-14],平面波激励,频率设定为5.6 GHz,远场RCS观测器。根据锥球体弹头形状的对称性以及为了计算的简便,假定锥球体轴线与锥球体运动方向平行,即φ=0°,分别以-180°~+180°的入射角扫描弹头,每次步进1°分别计算弹头的RCS值。
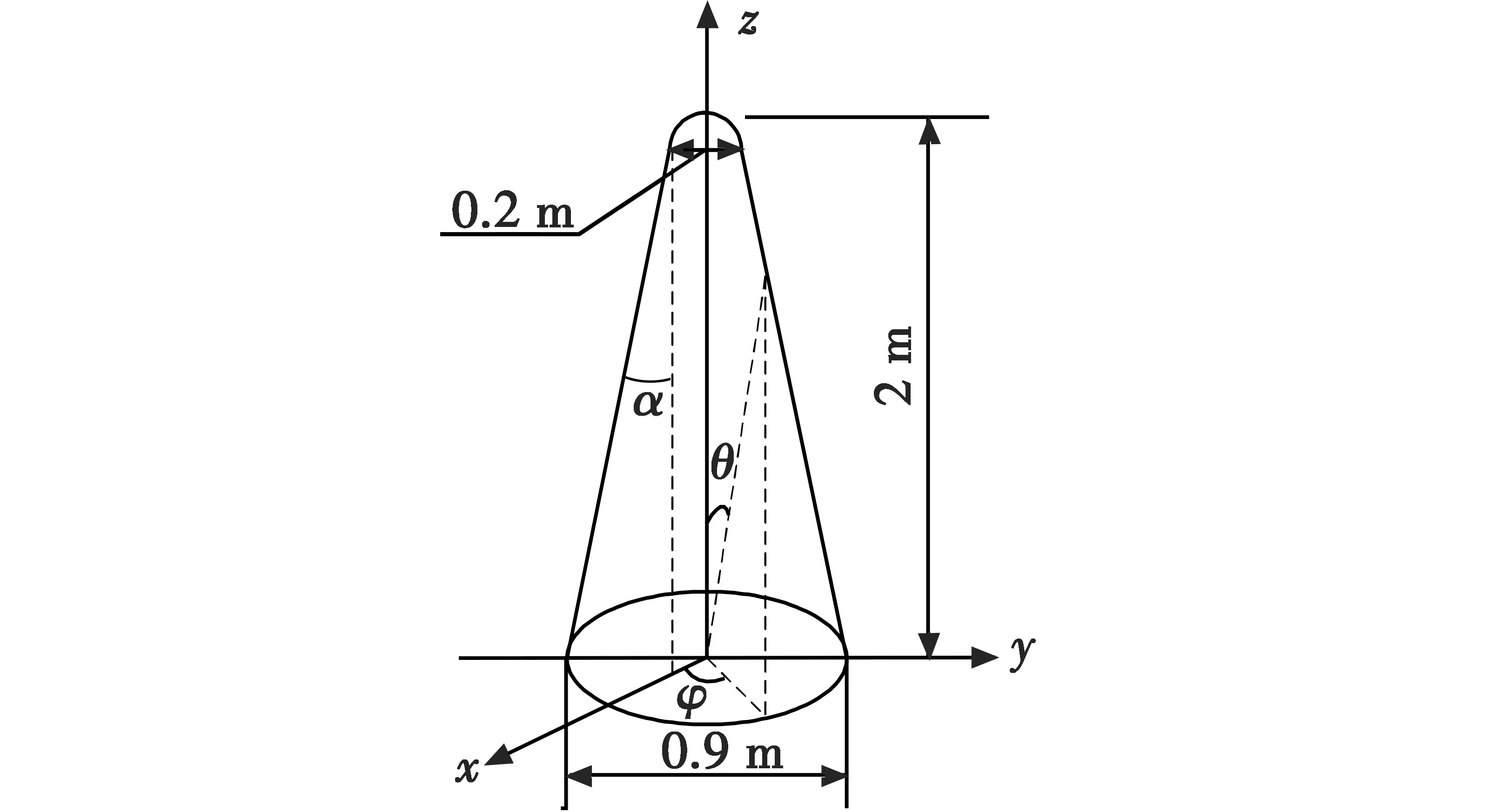
图2 锥球体弹头模型几何尺寸Fig.2 Scale of cone-spheroid warhead model
弹头的RCS计算结果如图3所示,横坐标是雷达视线与锥球体对称轴方向的夹角θ,纵坐标是在该视线下雷达波束照射后的RCS。从图3中可以看出,随着雷达视角的改变,锥球体的RCS值差异较大,在0°和±180°时,雷达波束对准弹头的两个端头,会出现较大峰值;在±80°附近也会出现一个明显峰值,雷达波束与锥球体的侧面边线垂直(锥球体的半锥角为10.4°),后向散射较强。其他雷达视角下RCS值做较小幅度波动,最后将计算得到的弹头RCS结果转存为数据列表待用。

图3 锥球体的RCS(φ=0°)Fig.3 RCS of cone-spheroid warhead while φ=0°
2.3 单部雷达目标检测仿真
单部雷达对弹头目标的检测为在获取弹头模型RCS的基础上,实时利用弹头与雷达间相对位置、雷达视角计算出其对弹头目标的检测概率。
仿真条件:弹头攻角为45°(弹头下落的过程中弹头的俯仰角和偏航角不发生变化),雷达工作频率采用5.6 GHz,虚警概率设定为10-6,雷达与被攻击目标间的距离为60 km,弹头垂直高度从100 km下降到20 km,射面角变化范围为0°~360°。
仿真内容包括: 1) 固定射面角为53°,弹头垂直高度从100 km下降到20 km,观察雷达的检测概率变化情况;2) 固定弹头垂直高度为30 km,射面角从0°变化到360°,观察雷达的检测概率变化情况;3) 同时改变射面角和弹头垂直高度,弹头的垂直高度从100 km下降到20 km,射面角从0°变化到360°,观察雷达的检测概率变化情况。
结合2.1节中的攻击、侦测过程,计算仿真步骤如下(见图4):
1) 根据雷达的频率和弹头的几何尺寸,在电磁仿真软件中计算出弹头在各雷达视角下的RCS值,转存为数据列表待用;
2) 设定弹头攻角∠HTM,雷达与被攻击目标间的距离RT;
3) 改变弹头垂直高度MH,模拟弹头下落的过程;
4) 针对弹头的每一垂直高度MH,改变射面角∠HTR,实时计算雷达、弹头间的斜距RM,雷达视角∠RMT;
5) 利用步骤4)中计算得到的雷达视角∠RMT从步骤1)中的RCS数据列表中得到弹头实时的RCS值;
6) 根据弹头的RCS值、雷达与弹头的斜距RM以及雷达的具体参数,通过雷达方程计算得到对弹头回波功率产生的检测信噪比RS,N;
7) 根据预设的虚警概率Pfa,利用Marcum Q积分就可以计算得到雷达的检测概率Pd;
8) 重复步骤4)~7),得到各高度、各射面角下雷达对弹头的检测概率。
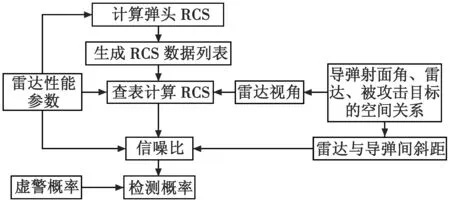
图4 单部雷达检测概率计算流程图Fig.4 Flow chart for computation of detection probability in single pulse radar
3 仿真分析与讨论
按照上述仿真条件及流程,得到的仿真结果如下。
1) 射面角为53°,弹头垂直高度从100 km下降到20 km,雷达对弹头的检测概率的变化情况见图5和图6。由图5可知,在射面角为53°时,随着弹头垂直高度的下降(100~20 km),雷达的视角从23°平滑上升到80°。由图6可知,随着弹头垂直高度的下降,检测概率整体趋势从0上升到1,并且在上升过程中出现了振荡、跳跃。由图3可知,在雷达视角为80°附近弹头的RCS存在一个极大值,此时的检测概率也会达到一个极大值,所以雷达视角从23°变化到80°,检测概率的整体趋势从0上升到1,并且从图3中可以看出RCS值的变化不是平滑的,存在剧烈振荡和跳跃现象,导致了检测概率的振荡和跳跃。
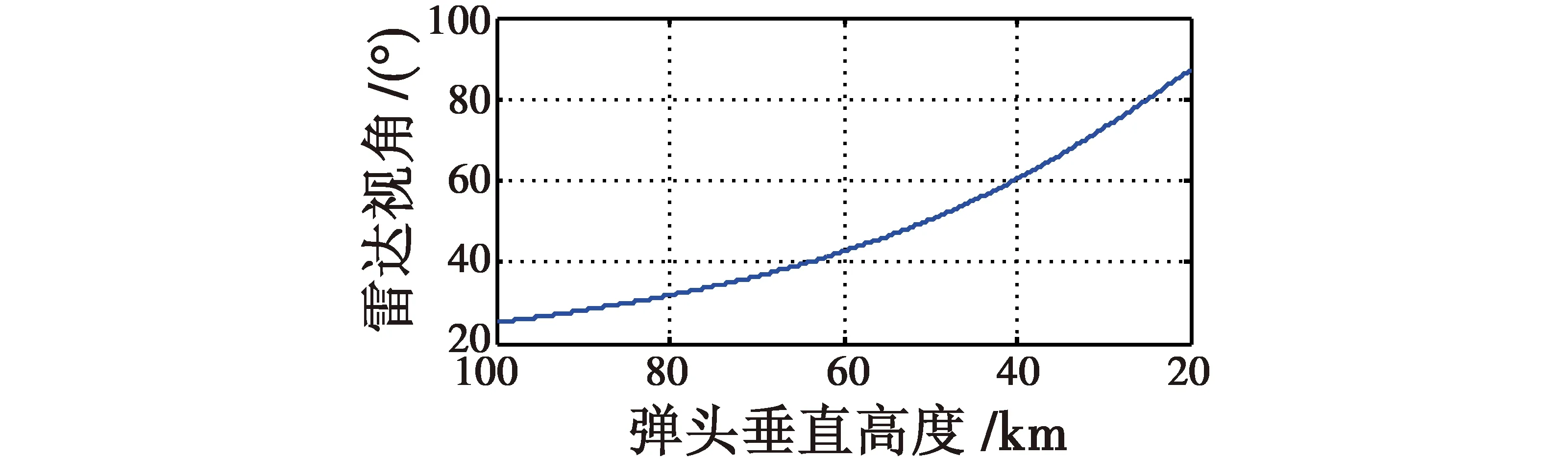
图5 雷达视角随弹头垂直高度变化曲线Fig.5 Influence of warhead height on radar aspect angle
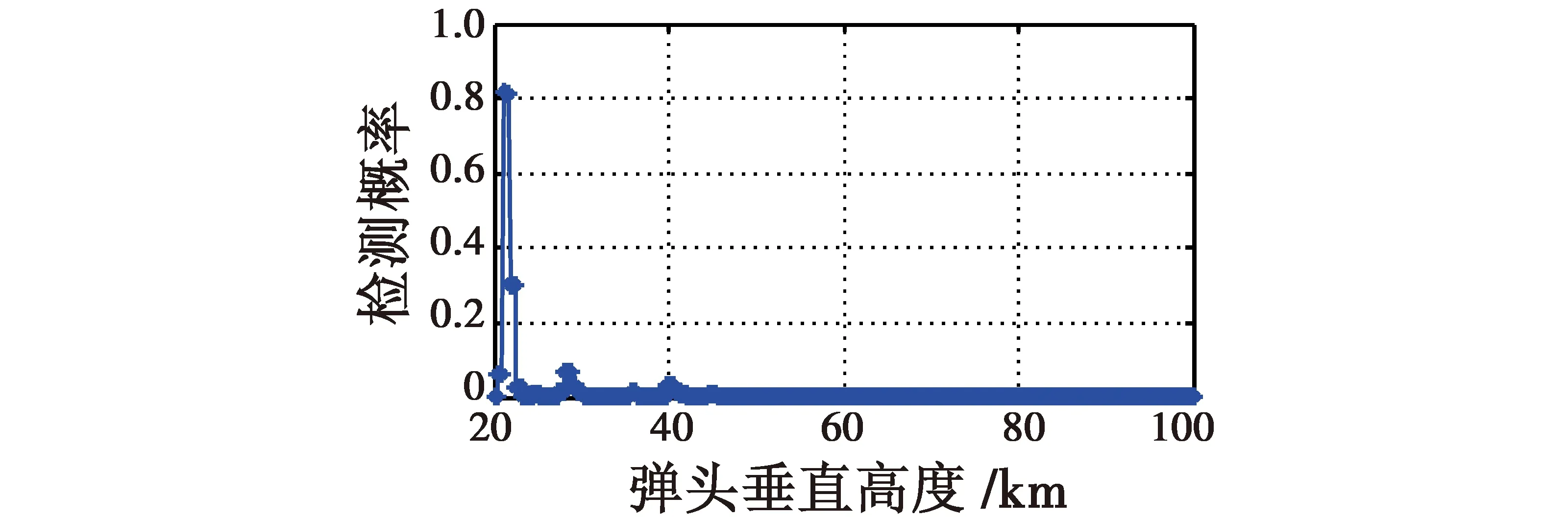
图6 检测概率随弹头垂直高度变化曲线Fig.6 Influence of warhead height on radar detection probability
2) 弹头的垂直高度为30 km,射面角从0°变化到360°,雷达对弹头的检测概率随射面角的变化情况见图7和图8。
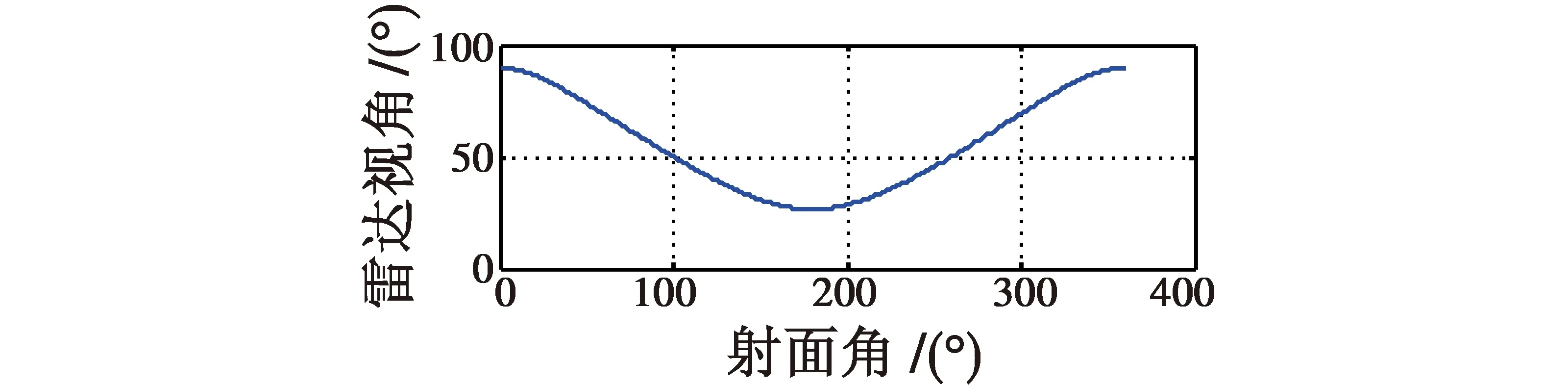
图7 雷达视角随射面角变化曲线Fig.7 Influence of launch angle on radar aspect angle at warhead height of 30 km

图8 检测概率随射面角变化曲线Fig.8 Influence of launch angle on detection probability
由图7可知,在弹头垂直高度为30 km时,随着射面角的变化(0°~360°),雷达视角从90°下降到23°左右后又上升到90°附近。由图8可知,在射面角变化过程中,检测概率在整体趋势上也从1下降到0,再从0上升到1;但在上升和下降的过程中,检测概率出现了剧烈的振荡和跳跃。具体的原因是射面角的变化引起了雷达视角的变化,但是弹头的RCS值与雷达视角的关系并不是平滑的,导致了检测概率的振荡和跳跃,具体见图8。
3) 弹头的垂直高度从100 km下降到20 km,射面角从0°变化到360°,雷达对弹头的检测概率的变化情况见图9和图10。
由图9中可知,射面角从0°变化到360°,雷达视角出现了两个波峰和一个波谷;弹头垂直高度从100 km下降到20 km,雷达视角呈上升趋势,从23°上升到了80°,其中,在射面角0°和360°附近时,雷达视角上升速度较快。

图9 射面角和弹头垂直高度对雷达视角的影响Fig.9 Influence of warhead height and launch angle on radar aspect angle
由图10可知,检测概率较高有两个区域,分别为射面角在0°~90°、弹头垂直高度为20~60 km和射面角在270°~360°、弹头垂直高度为20~60 km的区域,该区域内射面角和弹头垂直高度共同作用导致雷达视角落在20°到80°之间。在射面角为90°~270°,弹头的检测概率一直处于较低的水平。所以,如果考虑降低弹头的被检测概率,可以在设计弹道时将射面角设定为90°~270°。
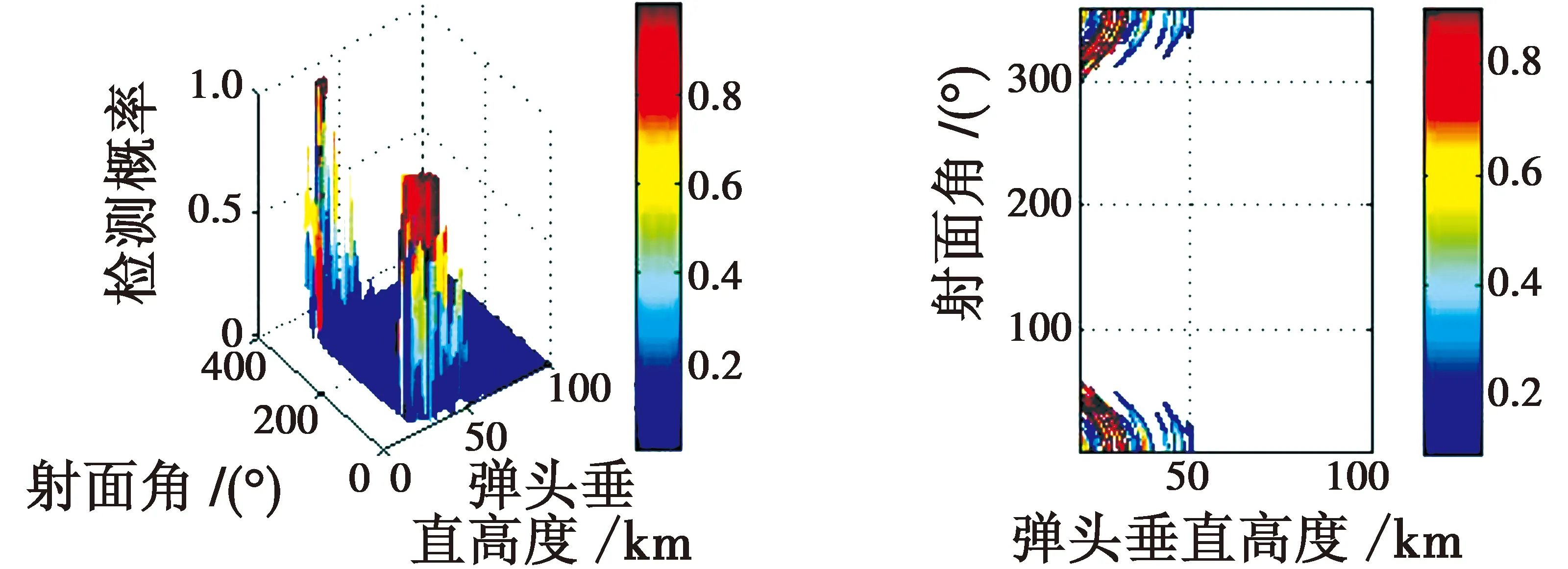
图10 弹头垂直高度和射面角对检测概率的影响Fig.10 Influence of warhead height and launch angle on detection probability
4 结论
本文首先运用电磁计算软件求出了锥球体弹头模型在不同雷达视角下的雷达散射截面积,再分别计算弹头目标在不同射面角和垂直高度下的被检测概率。结果表明检测概率较高的有两个区域,分别为射面角在0°~90°、弹头垂直高度为20~60 km以及射面角在270°~360°、弹头垂直高度为20~60 km的区域。在射面角为90°~270°,弹头的检测概率一直处于较低的水平。通过分析可知,弹道的射面角、弹头的垂直高度会引起雷达视角的变化,从而导致弹头的被检测概率的变化,所以在研究导弹突防问题时,可以考虑射面角的影响。另外,由于检测概率的变化源于雷达视角的变化,还可以考虑在弹道固定的情况下,通过调整弹头的姿态角,改变雷达视角,从而达到合理控制弹头的被发现概率,实现导弹突防的目的。
[1] 金圣彪.美国弹道导弹防御系统的发展现状及趋势[J].导弹与航天运载技术,2009(5):57-61.
[2] 王荣,张红军,王贵东,等.吸气式空空导弹外形多学科一体化优化设计[J].航空学报,2016,37(1):207-215.
[3] 罗志勇,郝璐.超声速飞行器隐身技术发展趋势分析[J].战术导弹技术,2016(2):16-22.
[4] 黄春华,刘凌宇,梁彦刚.高超声速滑翔飞行器再入拉起段弹道优化设计[J].战术导弹技术,2016(1):24-27.
[5] 雍恩米,钱炜祺,何开锋.基于雷达跟踪仿真的滑翔式再入弹道突防性能分析[J].宇航学报,2012,33(10):1370-1376.
[6] 杨正,曹志耀.防空警戒雷达以一种频率对空中目标的检测概率计算[J].电光与控制,2007,14(4):41-43.
[7] 吕栋雷,胡浩.雷达检测概率额计算[J].火力指挥与控制,2008,33(12):144-145.
[8] MERRILL I S.Radar handbook[M].3rd ed.New York:The McGraw-Hill Companies,2008.
[9] MERRILL I S.Introduction to radar systems[M].3rd ed.New York:The McGraw-Hill Companies,2001.
[10] BARICA A,MESZAROS T.Bounds for the symmetric dif-ference of generalized marcum Q-functions[C]//IEEE Jubilee International Symposium on Applied Computational Intelligence and Informatics,IEEE,2015:529-540.
[11] PARL S.A new method of calculating the generalized function[J].IEEE Transactions on Information Theory, 1980,26(1):121-124.
[12] 周超,张小宽,张晨新.再入段等离子体对弹头RCS的影响研究[J].现代雷达,2014,36(3):83-86.
[13] SONG J M,CHEW W C.Multilevel fast multipole algorithm for solving combined field integral equations of electromagnetic scattering[J].Microwave Optechnollet, 1995,10(1):14-19.
[14] GOMEZ-SOUSA H,RUBINOS-LOPEZ O,MARTINEZ-LORENZO J A.Multilevel fast multipole algorithm with multiple octrees for the solution of large-scale plasmonic problems with junctions[C]//European Conference on Antennas and Propagation,IEEE,2015:125-132.
DetectionProbabilityCalculationandPerformanceEvaluationofMonopulseRadar
QIN Jian-qiang1, KONG Xiang-yu1, HU Shao-lin2, MA Hong-guang3
(1.Rocket Force University of Engineering,Xi’an 710025,China; 2.Lab. of Fault Dianosis,Xi’an Satellite Control Center,Xi’an 710043,China; 3.Aviation Insitute of Zhuhai College,Beijing Institute of Technology,Zhuhai 519088,China)
In order to improve the survival probability of missiles in attacking process,the trajectory of it should be designed properly.Based on the monopulse radar performance indexes,the RCS values of a cone-spheroid shaped warhead are calculated out by using electromagnetic computing software.And detection probabilities of the warhead at different launch angles and different altitudes are computed out respectively.Numerical simulation results show that there are two areas where detection probability stays at a high level.One is that the launch angle is in the range of 0°~90°,while warhead altitude locates in 20~60 km;the other is launch angel is in the range of 270°~360° while warhead altitude locates in 20~60 km.The detection probability keeps at al low level when the launch angle is in the range of 90° to 270°.It comes to us that launch angle of missile should be selected carefully to keep the detection probability stay at a lower level.
missile; survival probability; trajectory design; RCS; detection probability;radar aspect angle
TN957.51
A
1671-637X(2017)03-0007-04
2016-02-25
2016-04-20
国家自然科学基金(61174207,61074072,61174138)
秦建强(1986 —),男,山西忻州人,博士生,工程师,研究方向为信号处理、故障诊断和非线性系统分析。
