帕斯卡尔的早期数学观

王幼军

(上海师范大学 哲学与法政学院，上海 200234)

帕斯卡尔的早期数学观

王幼军

(上海师范大学 哲学与法政学院，上海 200234)

数学是社会思想和文化的产物，几乎每一位数学家的数学观都受到其所生活的时代和环境的智识氛围、思想思潮和所有社会资源的影响。在这方面，帕斯卡尔早期数学观的发展变化提供了一个典型的案例，其典型特征是他关于数学的观点与其宗教追求密切地联系在一起，主要体现在其数学研究的动机、目标以及他对数学之于信仰的价值等问题坚持不懈的追求和思考上。帕斯卡尔的早期数学观深受以梅森为代表的巴黎数学家团体的影响；他们对数学的神圣性、有效性和确定性深信不疑，数学研究是其信仰的一部分。这种认识奠定了帕斯卡尔数学生涯的基础，他的数学实践深深地打上这种宗教数学观的烙印，其关于算术三角形的工作即是这种特色的典型体现。但同时，随着帕斯卡尔交往圈子的扩大，詹森主义者对数学之于信仰的价值的质疑以及德·梅勒爵士对于数学的确定性以及应用的局限性的质问，促使帕斯卡尔对其早期数学观进行反思。

帕斯卡尔；数学观；算术三角形；数学哲学

法国数学家帕斯卡尔(Blaise Pascal，1623—1662)的数学成就已广为人知，但是他关于数学知识的本质、方法和价值的观点以及数学研究的动机等方面却鲜为人知。作为17世纪最伟大的数学家、科学家和思想家之一，帕斯卡尔对于数学的认识也经历了如其多重身份一样的演化过程，特别是其早期数学观的形成和变化与17世纪欧洲的智识氛围和各种文化因素之间的关系比人们通常所认为的更加复杂和密切。本文基于前人的研究，旨在通过对帕斯卡尔的著作和其主要的精神生活节点的分析，来研究他的早期数学观的形成和演化过程，将着重强调其早期数学观的形成、它对于其数学实践的影响、它的转向，以及数学在更广泛的智识领域中的价值的思考。

一、早期数学观的形成

帕斯卡尔生活的17世纪被称为“数学世纪”，此时，无论是数学自身的发展还是数学在自然科学领域的应用等方面皆取得了引人注目的辉煌成就，数学的思想方法也被愈加广泛地引入到人类智识的所有领域，以求达到人类梦寐以求的数学般的确定性和有效性。17世纪30年代中期，被称为“梅森数学家沙龙”的学者共同体就是这个时代特色的一个体现，它是由梅森神父(Marin Mersenne，1588—1648)发起和组织的每周一次的学者聚会，先后参加的人员有罗伯瓦尔、德扎格、卡尔卡维、霍布斯、伽桑狄、笛卡尔等人。这些名噪一时的学者或是当时某一新数学领域的开创者，或是对数学推崇有加且极力倡导将数学理性精神推广至人学领域的思想家。关于这个学者团体的数学观和数学追求的动机，彼得·迪尔(Peter Dear)的研究表明，[1](P47)梅森创办的这个学术沙龙(有人也称之为梅森学派)兼有教育和学术研究的性质，其宗旨就是通过学者之间的交流，或者通过参加者的社会关系，寻求到那个时代具有“阿基米德式的”数学天赋的人才并给予系统的训练和培养，以期达到对古代数学的超越，从而极大地丰富数学的研究成果以及发现各种数学领域和对象之间的潜在关系；他们探讨数学的目的就是彰显数学知识的确定性、有效性和神圣性。

关于数学，梅森学派的基本观点有三个：一是强调数学作为人类知识基础的重要性，这种重要性的体现就是数学的绝对确定性，因为在宗教争论中这种确定性在消除怀疑论者的影响力方面起到了核心作用。梅森在《针对怀疑论者和皮罗主义者，科学的真理性》(1625)一文中说，数学是“极其确定和正确的科学，在其中根本没有悬置的位置”。[2](P54)二是强调数学的有效性，认为数学对于了解哲学、医学、炼金术、犹太神秘哲学、政治和法学以及机械学是必需的。梅森声称，如果一个人不想被排除在真正的学者团体之外，他就不能忽略对这门学科的研究，就像柏拉图拒绝那些“不懂几何者”进入柏拉图学院一样。三是强调对于几何学重要性的认可不仅是希腊哲学的基调，而且也是“基督教哲学”的基调。在标记为基督徒的这部书中，其最基本的特征就是数学，特别是几何学为通向神圣的上帝提供了独一无二的通道：数学乃是上帝在人间的镜像，数学有助于宗教的成熟。这种观点凸显了文艺复兴以后欧洲知识界所持有的一种崭新的数学观——宗教数学观。在梅森看来，这种数学观主要体现在上帝即是一位至高无上的数学家，数学某种程度是上帝的一个镜像反映。例如，神和一之间的对应关系既代表了简约性，又代表了创造的丰富性；上帝和圆之间的关系表明了上帝的永恒性。在数学中彰显上帝性质的例子不胜枚举，基于此，梅森认为阐释数学原理的创造性工作就是在模仿造物主的行为。数学的简单性、复杂性、丰富性和不可思议的有效性有助于向人类揭示上帝。通过模仿上帝这位几何学家，会使人的心灵转向自我超越，那些能够发挥其数学才能的个人会更加接近上帝的完美。梅森说：

在神学之后，没有一门呈现在我们面前的科学像数学那样让人看到了如此之多的奇迹，数学使我们的心灵超越了自己，也使我们意识到神(的存在)；它对静力学、水力学、气体力学也产生了令人不可思议的影响，看起来人类是可以模仿令人赞叹的上帝的作品的。[2](P59)

所以，对梅森和其追随者而言，数学追求的宗教意义不言而喻。这是鼓励他人投入到数学事业的宗教基础，在数学中致力于追求上帝的完美性成为数学研究的一个主要动力。这种动机之重要性的另一体现是：它刺激了怀有基督教信仰的人们对于具体的数学活动的热切追求以及基督教哲学家们对数学精神的更加广泛的探寻，通过对数学知识的不懈追求和勤勉的研究工作建立信仰成为他们的首要目标。梅森学派有一个雄心勃勃的计划：寻求前人尤其是希腊人未曾发现的数学不同领域之间的密切联系以及数学结果的丰富多样性，以彰显数学的无限潜力，从而揭示出上帝创造万物的奥秘和荣耀。就这样，梅森赋予几何学以神圣性的精神使命被其数学团体的成员们付诸实践，帕斯卡尔就是其中最杰出的实践者之一。

帕斯卡尔的父亲艾蒂安·帕斯卡尔也是一位数学家且与梅森学派交往甚密。1637年帕斯卡尔14岁时，在他父亲的引荐下进入这个圈子。梅森等人对于这位具有非凡数学天赋的少年器重有加并精心栽培，希望他能够成为新时期的阿基米德以达到“完美”数学这一目标。帕斯卡尔在梅森圈子中作为最年轻的参加者与其他会员的关系是亦师亦友，他在弥漫着浓厚的宗教数学思想的精神氛围中浸淫多年，即使在离开巴黎之后的许多年，他仍然经常回到这个沙龙参加活动并一直与之保持着密切的联系。自此，他的数学能力得以飞速发展，1639年16岁的他就完成了令笛卡尔深感惊讶的数学论文《圆锥曲线论》。

帕斯卡尔在那些尊崇数学的学者们的影响下度过了他的成长时期，他早期所处的智识氛围奠定了其数学生涯和精神生活的基础，他完全接受了梅森等人的宗教数学观。1640年帕斯卡尔举家迁往鲁昂时，他是带着在巴黎数学家团体中学习和感悟到的使命离开巴黎的，他尤其热切地将梅森学派所倡导的数学的宗教使命付诸具体的行动——通过研究数学的简单性、丰富性和不可思议的有效性，从而向世人揭示上帝的至高至美。帕斯卡尔以后的工作特征表现出梅森计划的持续性，即通过探索数学命题和结果的丰富多样性以达到“完美”的数学，他关于算术三角形的工作正是他早年接受的这种宗教数学观的延伸和体现。

二、早期数学观的实践：《论算术三角形》

1654年帕斯卡尔向巴黎数学学院提交了一篇演说词，在其中他勾画了数学和自然哲学活动的范围并提出了他的发表计划。这篇演说后来发表时被冠以《论算术三角形》之名，其内容是早已完成的几篇关于某些数的繁杂多样性质的论文组合。帕斯卡尔的算术三角形是由一些数字所组成的一个图式(见图1)，其每一格子中的数是通过一个简单法则从一个出发点自动生成的。这个出发点1在三角形的(左)顶端，生成的法则是：三角形每一格子中的数都是其上一行同列的格子中的数与同行前一列的格子中的数之和——C(n,k)=C(n-1,k)+C(n,k-1)。根据这个法则，这个“生成器”便会自动生成三角形的所有元素。这个法则就是帕斯卡尔所阐述的一些奇妙性质的最终来源。这篇长文由两部分组成，第一部分探讨了三角形中的数的多种性质，第二部分探讨了算术三角形在形数、组合论、概率论(赌注分配问题)、二项式展开等领域中的应用。[3]

图1 帕斯卡尔的算术三角形

对于帕斯卡尔而言，这个三角形的应用价值远远超越了一个数字图式本身，他的目标在于表明：在各种各样的推演中所显示出的只不过是一个思想产物的繁衍增殖。一些表面上看起来似乎毫不相干的领域——形数、组合论、概率论(赌注分配问题)、二项式展开——实际上只不过是一些相同数集的不同说法而已。这些特殊的数与离散的可数数也有关联，也与帕斯卡尔的抛物线下的面积求法有关，这些结果的令人惊异之处是揭示出离散与连续的领域竟然也有着密切的联系！在《思想录》中，帕斯卡尔把可数数与连续量(他简单地称之为“空间”)之间的联系做了进一步的扩展：“数目模仿空间，而空间的性质却是如此不同。一切都是由同一个主宰所造就和指导的：根茎、枝叶、果实；原则、结果。”[4](B119)这种差异巨大的不同实体(离散的可数数和连续的空间点)之间的密切关系，令人联想到或许存在于其他自然实体之间的隐蔽关系。这样，帕斯卡尔对各种数的探索也意味着对宇宙组成结构的探索，掌握和理解数学的法则有助于洞察上帝根据“数、测量和质量”运作自然的方式。他说：“经上说：‘上帝将一切事物置于数、测量和质量之中。’这三者就包含了整个宇宙。因此，数、测量和质量之间有着必不可少的相互关系。因为如果没有运动着的事物，我们就不能想象运动。这个事物就是1，它是所有数的起源，同样，如果没有空间，运动也就不能存在，由此看到，这三样事物都蕴含于第一个(数)之中了。”[5](P122)

对于这些数的研究能够揭示出数、测量和质量之间的密切关系，人类能够拥有这些存在之关系的确定性知识，即使不了解隐匿于它们背后的原因和理由。这种知识是确定的、清晰的、明白的和完备的，即使不是由因果推理得到的。

自然对于自身的模仿也可以扩展到人类活动中：“自然模仿其本身：一粒谷子种在好的土地上就有出产；一条原则种在好的精神里也有出产。”[4](B119)在论文中，帕斯卡尔发现了基于某种方法的一些不可思议的联系。这种方法也有助于培养创造性的心智和激励人类理性的信心。这种心智具有超乎人想象的掌握众多法则的潜力，能够清晰地阐明这些不同的法则集合之间的关系，因此这种心智能够窥视如空间和时间等超越数学概念的一些思想，由此更加接近如无限等超越的神学思想。

丹尼尔·朱利彻(Daniel Julich)认为，[2](P226)帕斯卡尔对于其算术三角形的描述明确地凸显了他和梅森的宗教数学观之间的相似性。这表现在他对几何学家目标的清晰论述：几何学家的工作就是朝向“繁荣命题”的目标，为的是发现众多“丰富多样的、伟大的定理”，从而达到模仿上帝的目标。另外，帕斯卡尔在文章中重申了梅森关于数学的繁殖能力的强调。例如，梅森把数“1”描述为上帝的镜像之一，它是不可再分割的，它会产生“蕴含于数中的所有完美性”；这就像上帝的简单性，也像上帝的丰饶多产性，通过操作能够产生无限多的整数。可以说，帕斯卡尔努力发现算术三角形的各种交叉性质的动力与梅森的信念是一致的，可以说是梅森的“通过数学能够提升自己至神圣完美境界”的信念的扩展。

从1648至1654年这段时期，是帕斯卡尔短暂一生中健康状况较好的时光，是他的数学和物理研究最旺盛的阶段。其工作的特征非常明显地遵循了梅森为数学设置的目标，通过丰富数学领域的成果和建立数学领域之间的新联系，致力于追求至美的数学状态，以达到对于造物主的虔诚模仿。对此时的帕斯卡尔而言，数学即为宗教信仰中精神生活的一部分，是一种灵性的操练，也是为成熟信仰所做的精神准备。然而这种理性的宗教数学观正在随着他与詹森主义者的交往而发生变化。

三、早期数学观的转向

詹森主义是17世纪在天主教内部兴起的一场神学运动，其发起者康内留斯·詹森(Cornelius Jansen, 1585—1638)是一位坚定的奥古斯丁主义者，詹森及其追随者完全接受了奥古斯丁关于罪和恩典的教义，强调人性的彻底堕落，强调神的恩典对救赎的必要性以及神圣的预定等观点。詹森主义者认为其对手耶稣会士过于强调人的理性，借由自由意志而夸大人的自主性，以至于使耶稣救赎的工作成了廉价的恩典。相对于耶稣会士，詹森主义者更加强调常识、习惯和生活方式对于信仰的重要性，号召其教徒过极度虔诚的生活。1646年，时年23岁的帕斯卡尔首次直接接触詹森教派的德尚兄弟。那一年帕斯卡尔的父亲艾蒂安由于跌倒而导致大腿骨受伤，善于正骨术的德尚兄弟来到帕斯卡尔家中照料艾蒂安三个月直到其康复。在此期间，帕斯卡尔系统地研习了詹森教派的教义，他开始相信这个有些激进的教派比流于形式的传统天主教更有价值，由此激起了他对信仰的空前热情；触动他的正是这个教派强调常识、习惯和生活方式对于信仰的重要性，他把这次经历称为自己的“第一次皈依”。

1647年以后，帕斯卡尔本人一直与詹森派的大本营罗亚尔港(Port Royal)保持着密切的联系。詹森教派的灵修导师不赞成帕斯卡尔只安于做一位有宗教信仰的学者，他们认为，说宗教学者是通过研究和学问来寻求体现其献身精神的人，这只是不知天高地厚的知识分子的狂妄，真正信仰的培育乃是源自人的直接体验。詹森主义提供的精神影响使得帕斯卡尔开始重新评估其早先的数学观，他开始领悟数学的局限性，开始认同“数学只不过是一种技能或手艺”的观点。1647年9月，妹妹雅克琳在写给姐姐吉尔伯特的一封信中提到帕斯卡尔甚至说自己“不再是一位数学家”，[2](P198)他的兴趣更多地转向宗教的活动与沉思。在1648年1月，帕斯卡尔在写给吉尔伯特的信中明确强调：“正是常识所指导的理智使人相信，即使不借助推理也必须相信。”[2](P198)对于新思想路径的明显兴趣和不情愿被认定为一个单纯的数学家表明：其观点已偏离了梅森学派的观点——数学工作本身就是一种精神灵修工作。罗亚尔港施加的影响促进了这种认识的转变：从理性的宗教数学观到虔诚信徒的训导和操练。

从现有的文献资料来看，帕斯卡尔关于数学局限性意识的觉醒还有赖于他曾经结交的世俗贵族朋友德·梅勒爵士(Chevalier de Mere，1607-1684)的影响。德·梅勒接受过良好的古典教育，他在《论精神》(1677)一书中谈到的一次旅行，为我们了解帕斯卡尔数学思想的转型提供了一些线索。这次旅行大约发生在1651或1652年，在梅勒看来，那时帕斯卡尔的兴趣范围仍然局限在数学上，其作为一个有天赋的个体范例还没有表现出理解力的广度；但是，通过与骑士和其他两位朋友仅仅几天的谈话和讨论，帕斯卡尔就从一个“既没品位，也没情趣的人”转化到了一个能够超越自身本然和天赋才能的境界。[6]

梅勒认为，此时的帕斯卡尔尽管由于其无与伦比的天赋，在数学、算术机以及其他实验领域做出了引人注目的成绩，但是他的这些活动仍停留在匠人般本能的原始状态——他们只在天赋本能所驱使的范围内进行操作，就如钟表匠制造钟表这类有限的技艺一样。对于梅勒来说，数学的局限性主要表现为其范围的局限性，数学家是如此专注于一些抽象的法则，以至于他们无法有意义地从事其他学科。数学尤其不能满足于人的领域，因为它无法将各种主题传达给各种各样的人。这正是帕斯卡尔在写作《思想录》时所意指的局限性，他写道：“我曾经长时期从事抽象科学的研究，而在这方面所能沟通交流的人数之少使我失望。当我开始研究人的时候，我就看出这些抽象科学是不适宜于人的。”[4](B144)

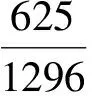
梅勒由此意识到数学的局限性以及他对于数学的确定性和有效性的怀疑，他要促使帕斯卡尔从其数学至高的梦幻之中醒悟，尽管数学是世界上“最优秀的技艺”。这种提醒加强和鼓励了帕斯卡尔从詹森主义者那里受到的启发：数学与科学活动并非完全献身于上帝的最重要的职责。学者梅斯纳德(Mesnard)认为，[7](P256)梅勒多年后凭记忆记述的他与帕斯卡尔的交往夸耀了自己在促使帕斯卡尔重新评估数学的转变中所起的作用，尽管如此，在梅勒炫耀夸张的叙述的背后隐含了一些具有启发性的信息，那就是：帕斯卡尔的快速转换表明他已经处于多种思想交叉混合的突破时期。梅勒与其他一些世俗之士的观点有助于使帕斯卡尔进一步理清和摆脱数学技艺的局限性，他早期的训练曾经将他牢固地禁锢在这种局限之中。

梅勒的综合思考与詹森主义者宗教奉献的诉求在帕斯卡尔的思想和生活的各个方面都产生了共鸣，但这种影响还没有显现出立竿见影的效果，早期的数学观念仍然由于惯性在影响着帕斯卡尔，数学继续占据着其生活的主要方面。直至1654年11月，以“火之夜”[8](P20～21)而著称的一次神秘的体验给予帕斯卡尔一些前所未有的感受，这是他的数学思考和其他科学活动从未给予他的。从此他全心倾注于宗教的活动和沉思，对于数学，他开始转向一种更广阔的视角，尤其转化为对数学的确定性和局限性的反思，其后期的数学观最终定位于《论几何学的精神》[9]和《思想录》[4]两部作品之中。对于此时的帕斯卡尔而言，数学的确定性和局限性正反映了人作为被造物的有限性与试图追求完美性和超越性的悖论处境，这种数学观的核心论点在其著名的赌注论证中得到了充分的展现。[10]

概而言之，帕斯卡尔早期数学观的形成和演化始终与他所处的时代和社会的智识氛围有着极为密切的关系，这表现为激发其数学研究动机的宗教因素、他对数学知识的本质和方法的思考，以及在数学的价值等方面坚持不懈的追求和思考上。帕斯卡尔在少年时代深受以梅森为代表的巴黎数学家团体的影响，他们皆对上帝乃是一位至高无上的数学家以及数学的至高至美和确定性深信不疑。对他们而言，数学研究是宗教信仰的一部分。这种宗教数学观是帕斯卡尔早年数学生涯和精神生活的基础，并对他的数学实践产生了极大的影响。后来由于受到詹森主义者对数学在信仰中的价值的质疑以及德·梅勒爵士对数学的确定性及其应用的局限性的质疑的影响，他开始了对数学的局限性的思考；但在实践上，此时是其数学创造力最旺盛的时期，关于算术三角形以及概率论等方面的研究是早期形成的宗教数学观的惯性驱动使然。而最终，随着帕斯卡尔全心倾注于宗教的信仰，他放弃了早期所崇尚的数学神圣的观点，而更多地转向了数学对于信仰的有限价值的反思。

[1] Peter Dear. Mersenne and the Learning of the Schools[M]. New York:Ithaca, 1988.

[2] Daniel Julich. Pascal, Devout Savant: Science, Religion,and the Learned Community in Seventeenth-Century Paris[D]. A Dissertation for the PH.D., University of Florida, 2009.

[3] A. W. F. Edwards. Pascal’s Arithmetical Triangle[M]. New York: Charles Griffin, 1987.

[4] 帕斯卡尔.思想录[M].何兆武,译.北京：商务印书馆，1997.

[5] Matthew L. Jones. The Good Life in the Scientific Revolution: Descartes, Pascal, Leibniz and the Cultivation of Virtue[M]. Chicago: University of Chicago Press，2006.

[6] Oystein Ore. Pascal and the Invention of Probability Theory[J]. The American Mathematical Monthly, Vol. 67, No. 5, 1960.

[7] Mesnard. Pascal et les Roannez[M]. Vol.1. Paris: Desclée De Brouwer, 1965.

[8] 道格拉斯·格鲁休斯.帕斯卡尔[M].江绪林,译.北京：中华书局，2003.

[9] Blaise Pascal. “On the Geometrical Spirit”, Miscellaneous Writings of Blaise Pascal[M]. London: Longman, Brown, Green, and Longmans Paternoster-Row, 1849，73-76.

[10] 王幼军.帕斯卡尔赌注的形式演化[J].上海师范大学学报(哲学社会科学版)，2015,(4).

OnPascal’sEarlyViewsonMathematics

WANG Youjun
(College of Philosophy, Law and Politics, Shanghai Normal University, Shanghai 200234, China)

Mathematics is the product of social culture. Almost every mathematician’s mathematical view was influenced by the intellectual atmosphere of his times and the environment, and all the social resources. In this respect, the development of Pascal’s early mathematical concept provides a typical case, whose typical characteristic was that Pascal’s views on mathematics were closely connected with his pursuit of religious spirit, his motivation of doing mathematics, the methods of mathematical research, and the perennial pursuit of the relations between mathematics and knowledge, transcendence and salvation. Pascal was influenced in his boyhood by Mersenne’s cycle, which was a group of mathematicians in Paris. They thought of God as a supreme mathematician and mathematics as a Divine Science with certainty of supreme beauty, thus there is a clearly religious significance in the pursuit of the mathematical sciences. This faith laid a foundation for his mathematical career and spiritual life. Pascal’s mathematical practice is deeply imprinted on this religious mathematical concept, and his work on arithmetic triangle is a typical manifestation of the characteristic. At the same time, Jansenist’s questioning of the sufficiency of mathematical reasoning in faith and Chevalier de Méré’s suggestions that mathematics was of dubious value awakened Pascal’s reflection on the suitability and limitations of mathematics.

Pascal, views on mathematics, arithmetic triangle, philosophy of mathematics

N031

A

1004-8634(2017)06-0115-(06)

10.13852/J.CNKI.JSHNU.2017.06.015

2017-03-09

上海高校高峰高原学科建设计划资助

王幼军，上海人，上海师范大学哲学与法政学院教授，博士生导师，主要从事数学史、数学哲学研究。

(责任编辑：法 芒)