液桥内热质耦合对流不稳定性及旋转磁场法控制1)

邹 勇 朱桂平 李 来 黄护林,2)

*(南京航空航天大学能源与动力学院，南京210016)

†(安徽工业大学数理学院，安徽马鞍山243032)

液桥内热质耦合对流不稳定性及旋转磁场法控制1)

邹 勇*,†朱桂平*李 来*黄护林*,2)

*(南京航空航天大学能源与动力学院，南京210016)

†(安徽工业大学数理学院，安徽马鞍山243032)

浮区法因具有无坩埚接触污染的生长优点而成为生长高完整性和高均匀性单晶材料的重要技术.但熔体中存在的毛细对流会给浮区法晶体生长带来极大挑战，这是由于对流的不稳定会导致晶体微观瑕疵的产生和宏观条纹等缺陷的形成.为了提高浮区法生长单晶材料的品质，研究浮区法晶体生长中毛细对流特性及如何控制其不稳定性显得尤为重要.本文采用数值模拟的方法对半浮区液桥内SixGe1−x体系中存在的热质毛细对流展开研究并施加旋转磁场对其进行控制.结果表明：纯溶质毛细对流表现为二维轴对称模式，温度场主要由热扩散作用决定，而浓度场则由对流和溶质扩散共同支配；纯热毛细对流呈现三维稳态非轴对称流动，浓度分布与熔体内热毛细对流的流向密切相关，等温线在对流较大的区域发生弯曲；耦合溶质与热毛细对流则为三维周期性旋转振荡流.施加旋转磁场后，熔体周向速度沿径向向外增大，熔体内浓度场和流场均呈现二维轴对称分布.

浮区法，毛细对流，表面张力，数值模拟，旋转磁场

引言

浮区单晶生长技术[1-3]作为无坩埚法，是制备单晶的一种重要方法，广泛用于高精度硅、高温合金及其他半导体材料的生长[4-5].浮区法晶体生长是一个包含固体导热、熔体对流、固液相变等多种传热流动方式的复杂热--质输运过程.生长过程中的传热流动特性直接影响功率消耗、温度分布、界面形状等宏观晶体生长参数，并最终决定单晶内部的微观结构和缺陷、杂质的分布.因此，有必要深入研究熔体中的热质流动特性并对其进行有效控制，以改善单晶质量[6-9].由于浮区单晶生长中存在着自由表面，表面张力驱动的马兰哥尼(Marangoni)对流对熔体中杂质浓度的分布会产生极大的影响[10].单晶中杂质分布的不均匀性是制约晶体质量的主要因素之一，它所导致的材料光学、电学性质的不均匀性将最终损害半导体电子和光电子器件的性能.要想充分利用浮区结晶法的优点生长出高品质的单晶，首先必须了解杂质分布不均匀性的起源和形成，即晶体生长中的杂质分凝现象.晶体生长过程中，生长界面处的杂质浓度分布除了受温度场支配的生长界面的形状、稳定性的影响之外，还由质量输运过程决定，即通过扩散过程和伴随对流过程(动量输运过程)实现.扩散过程由熔区内的浓度梯度驱动，而动量输运过程则紧密依赖于熔区内的流场.

目前，人们对于单纯的热毛细对流稳定性从实验[11-13]和理论[14-16]上已有较深入的研究.结果表明：随着温差增大，马兰哥尼对流将发生失稳并出现热流体波不稳定性；进一步增大温差，流场将出现更为复杂的振荡流动，其振荡特性与马兰哥尼数Ma有关.在地面条件下，热毛细对流还将和重力产生的自然对流耦合在一起[17-19].吴勇强等[18]采用2cst硅油实验研究了矮液桥浮力--热毛细对流的起振及转捩到混沌的过程，并分析了不同液桥的温度振荡频率及相位变化情况.结果发现，液桥高径比、体积比对起振温差及振荡频率都有很大的影响.随后，王佳等[19]对大尺寸液桥内部的浮力--热毛细对流流场结构和流动模式展开研究.实验发现在临界Ma附近，流场内会出现行波现象，流动模式也会随高径比的变化而发生变化，继续增大Ma，流动会进入混沌状态.

实际上，由于半导体晶体的掺杂需要，尤其是合金材料，在浮区生长中，熔体中存在着很大的浓度梯度，这将引起强烈的宏观分凝.表面处的浓度梯度诱导溶质毛细对流，这种毛细流和由温度梯度产生的热毛细对流耦合在一起，形成复杂的流动.Lyubimova等[20-21]利用线性稳定性方法分析了浮区晶体生长中不同情况下三维热--质耦合对流的发展过程，获得了非轴对称对流随时间演化的特性和结构图像.从他们得到的不同结晶速度和高径比参数下热马兰哥尼数MaT--溶质马兰哥尼数MaC的稳定性平面图可以看出：即使是弱的溶质对流扰动也会引起热毛细流动稳定性的大幅变化；弱的热毛细效应的存在同样会对溶质毛细流的稳定性造成较大的影响.Minakuchi等[22]以全浮区液桥模型研究了零重力下溶质--热毛细耦合对流，得到结论是尽管MaC比MaT大，但是自由表面上由浓度梯度引起的轴向对流强度反而比热毛细对流小.在国内，游仁然和胡文瑞[23]首先采用了液桥模型开展耦合热--质对流的研究，他们发现MaC对液桥中的流场和浓度场具有重要影响，但对温度场分布的影响较弱.Zhou和Huai[24]对具有变界面的液桥中的热毛细对流和溶质毛细对流进行了数值分析，研究发现，当MaT与MaC的比值为−1时，自由表面在冷、热两端凸出而中间收缩.目前，这些研究的重点主要集中在毛细对流的特征上，在毛细对流的控制方面的研究相对较少.

由于硅、锗等熔体具有良好的导电性，通过外加磁场可有效地抑制熔体流动并影响热质传输，从而减少晶体的生长条纹，控制晶体生长的界面、杂质的分离等.各种外部磁场[25-29]中，旋转磁场具有低功耗的特点，其在导电熔体中产生洛伦兹力不仅能够增加传质速率，还能增强熔体流动的稳定性，因此施加旋转磁场对导电熔体进行主动控制是可行的.目前为止，旋转磁场已用于Czochralski法[30-31]、液相扩散法[32]、Bridgman法[33]及浮区法[28-29]等晶体生长中，相应的理论分析及实验研究已经展开，取得了一定的成果.鉴于理论分析和实验研究在高温条件下存在的困难，目前仅有少量实验报道溶质毛细对流对Si-Ge浮区晶体生长的不利影响[34]，利用旋转磁场对Si-Ge体系中毛细对流进行控制的研究尚未见报道.本文采用半浮区液桥模型，通过数值模拟研究SixGe1−x体系中热质毛细力对熔体对流的贡献，对比分析各种毛细对流的特征以及旋转磁场下熔体的传热传质流动特性.

1 物理数学模型

本文计算采用了柱坐标系(r,θ,z)下的半浮区液桥模型，物理模型如图1所示.在零重力条件下，不考虑自由面的变形，即认为液桥自由面为圆柱面，液桥高为L，悬浮在具有相同半径R的圆盘之间，将固液界面简化为无滑移平面，分别位于z=0和z=L处并保持温差∆T(∆T=Th−Tc)不变.

假设熔体为不可压缩的牛顿型黏性流体，表面张力作用在自由表面上，其大小可表示为温度及浓度的线性函数[24]

式中σ0=σ(T0,C0)，γT=∂σ/∂T，γC=∂σ/∂C,C为浓度.只考虑表面张力随温度升高而减小，随溶质浓度增大而增大这一特殊情况.假设流体的其他物性不随温度变化而仅随浓度变化，且与浓度呈简单的线性混合规律.施加的外部旋转磁场强度和频率分别为B0和ω，其分布可表示为[28-29]

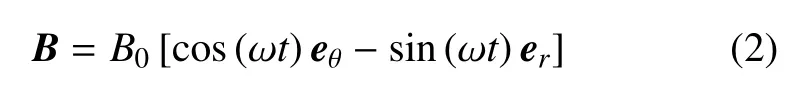
式中，eθ和er分别是轴向和径向单位矢量.

基于以上假设，外加旋转磁场作用下，熔区内磁流体动力学方程组可表示为

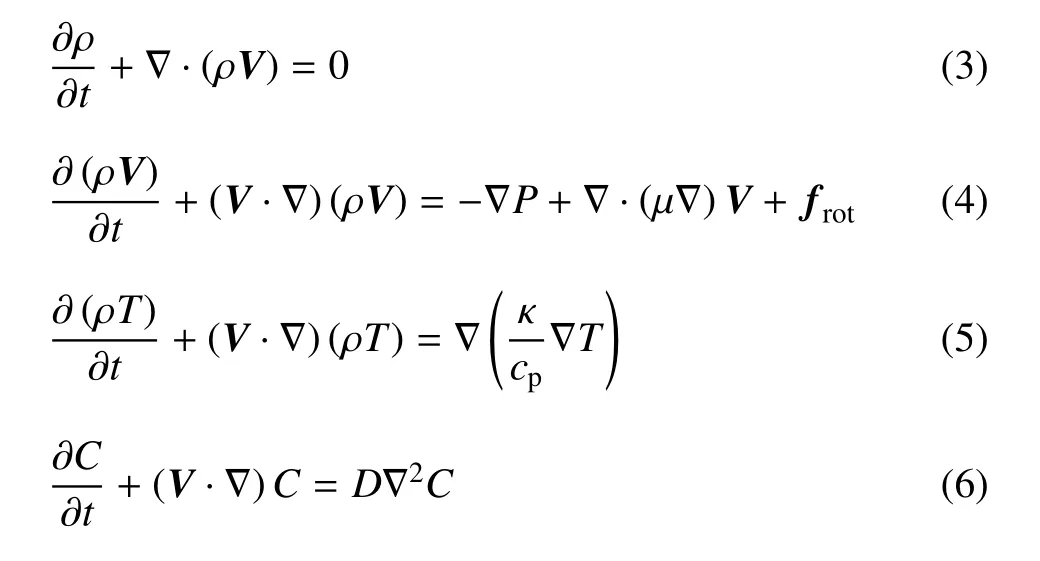
式中，∇是在柱坐标系下的算符，V是速度矢量，T为熔体温度，C为熔体中Si的质量浓度.ρ为熔体密度，P为压力，µ为动力黏度，κ为导热系数，cp为比定压热容，D为Si在Ge中的扩散系数.假设混合熔体的物性与Si浓度呈简单的线性关系，即ρ=CρSi+(1 −C)ρGe，µ=CµSi+(1 −C)µGe，κ=CκSi+(1−C)κGe，cp=CcpSi+(1−C)cpGe.旋转磁场在熔体内部产生的洛伦兹体积力可表示为[35]其中σe为电导率.

边界条件和初始条件设定如下：

当z=L时

当z=0时

当r=R时

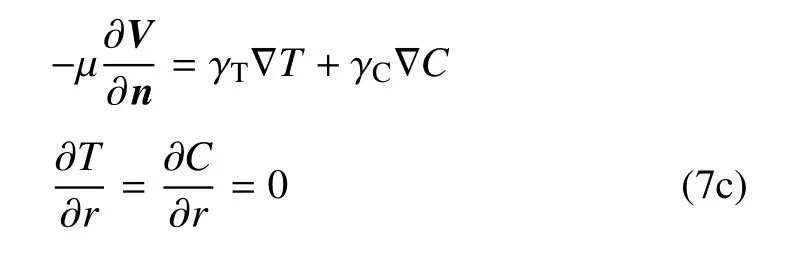
当t=0时

式中，n是自由表面的法向矢.

表1 SixGe1−x体系物性参数[34,36]及其他计算所需参数Table 1 Physical properties of the SixGe1−xmelt[34,36]and other parameters needed

2 计算方法

采用非结构化网格的有限体积法对控制方程进行空间离散，并在自由表面及交界面附近进行局部加密，网格独立性验证曲线如图2所示，其对应的网格量如表2所示.由图2可见，当网格数大于20万时，液桥内监测点P(r=R,θ=0,z=L/2)的无量纲温度最大值变化较小，综合考虑计算准确性和计算时间，选择40×80×80(r向×θ向×z向)的网格进行数值计算.计算中采用时间步长为10−3s.对动量方程、能量方程中的对流项采用QUICK格式离散，扩散项都采用二阶中心差分离散，时间项采用二阶隐式推进法，压力速度耦合采用PISO算法.算法的正确性同文献[37]的结果进行了比较.表3显示的是当Pr=0.01,Re=3500时，相同模型下熔体中最大速度值umax和周向最大速度值wmax同文献[37]的对比结果，可以看出，两者基本吻合.

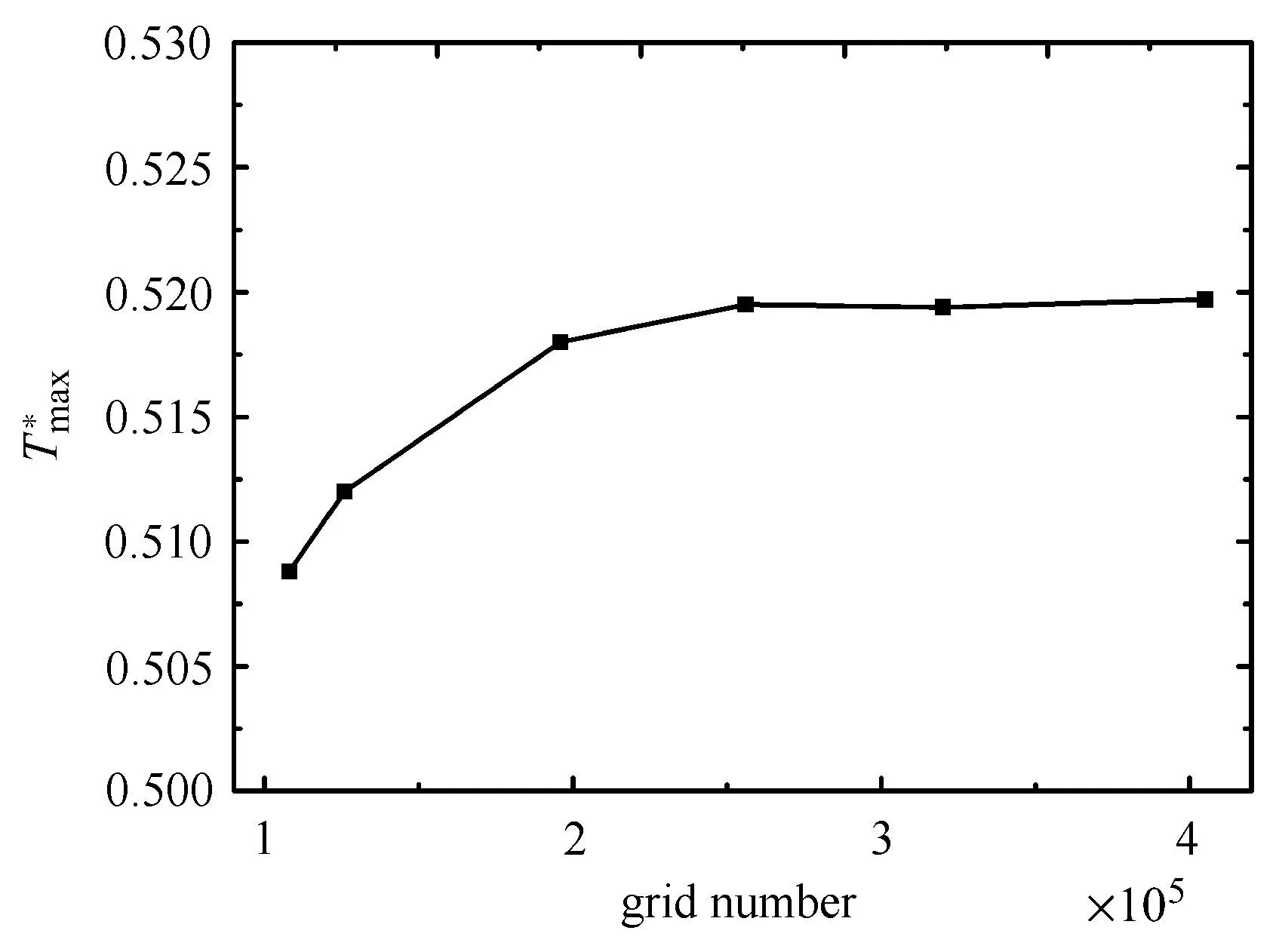
图2 网格独立性验证曲线Fig.2 Grid independence veri fi cation curve

表2 网格量Table 2 Grid numbers with di ff erent meshes

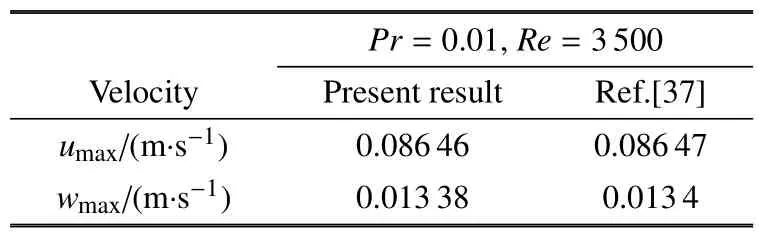
表3 本文和文献[37]的计算结果对比Table 3 Comparison of the present result and the result of Ref.[37]

3 结果与分析

3.1 无磁场时熔区内毛细对流特征

零重力环境下，由重力引起的浮力对流消失，晶体生长过程中熔体质量的输运，主要依赖扩散，因而可实现纯扩散晶体生长过程以获得较大的浓度梯度，同时又可以避免不稳定浮力流对晶体质量的影响.但在空间浮区法晶体生长过程中，虽然克服了浮力对流的作用，但由表面张力梯度驱动的马兰哥尼对流在熔区中占据主导地位.本文中由于所研究的SixGe1−x体系中溶质Si浓度很大，自由表面溶质毛细力的影响亦不容忽视.数值结果表明，当仅考虑溶质毛细力时，由其驱动的对流沿自由表面从Si浓度较低的下底面流向浓度较高的上底面，在子午面内形成左右两个对称的对流涡，并在液桥中心区域形成逆向回流涡，结果如图3(a)所示.在扩散作用下，同时受对流影响，子午面上半部Si浓度等值线(虚线所示)呈“W”型分布(由对称性只显示右半部)，但是，由于熔体的普朗特数远小于施密特数，温度等值线仍呈平行分布(图中左半部点划线所示)，这与游仁然和胡文瑞[23]得到的关于溶质毛细对流对温度场影响较弱的结论是一致的.中截面z=L/2上速度轴对称的分布特点(图4(a))表明熔体中对流是二维定常流.

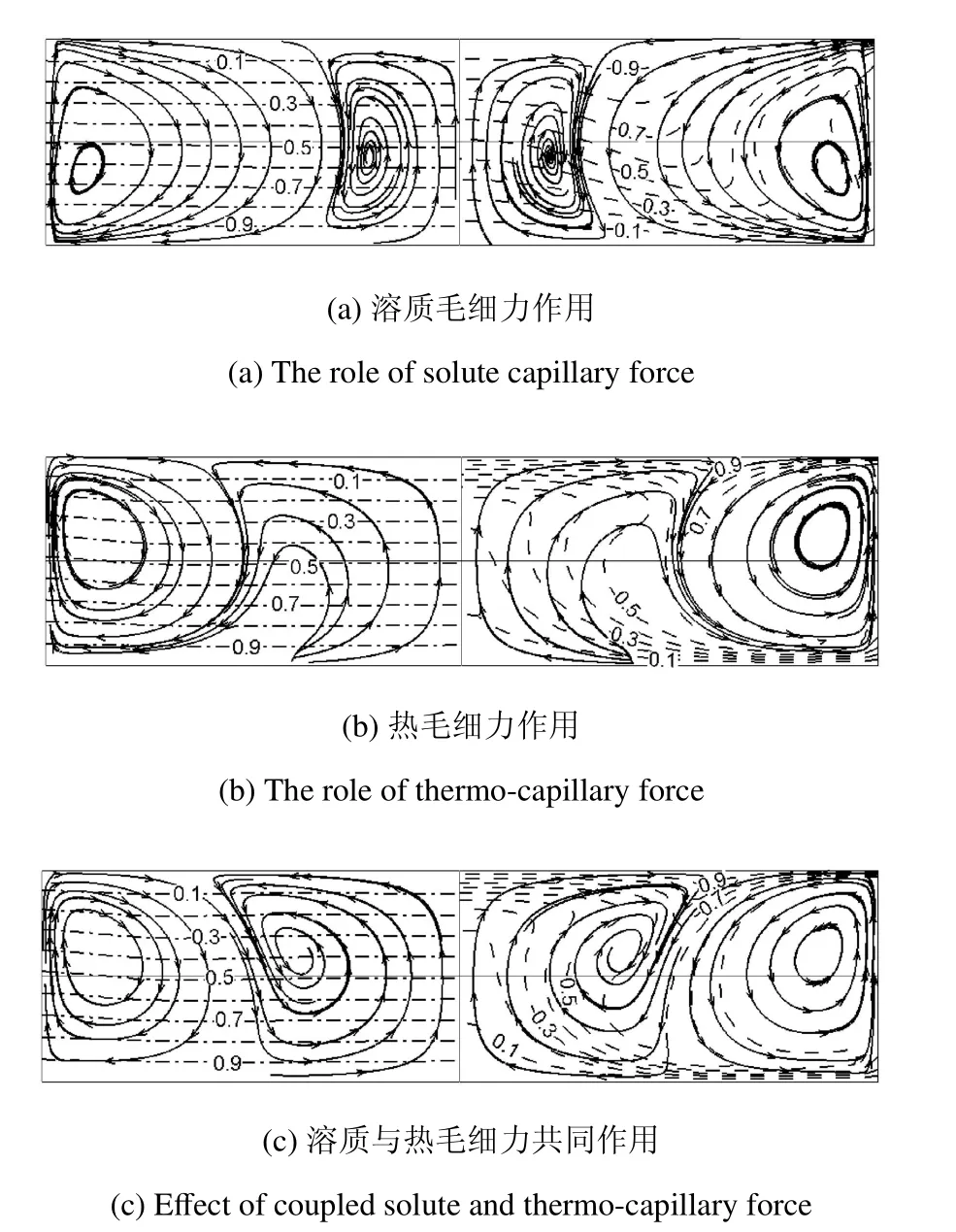
图3 无磁场时子午面上流线(实线)、无量纲温度(T*)(左边点划线)和Si浓度(右边虚线)分布图Fig.3 Streamline(solid line),dimensionless temperature(T*)(dash-dot line in the left)and Si concentration(dashed line in the right)distribution on the meridian plane without magnetic fi eld

熔体在热毛细力的作用下，对流结构明显不同于溶质毛细对流，由图3(b)不难看出，虽然热毛细对流在子午面内也形成左右两个对称的对流涡，但并未在液桥中心区域形成完整的回流涡.两种对流涡心位置也有很大的不同，溶质毛细对流涡心在中截面下方，而热毛细对流的涡心在中截面的上方.由于热毛细对流比溶质毛细对流强度大，所以回流速度也较大，液桥底部Si浓度较低的熔体被输运到液桥上方区域，在上底部附近形成较大的浓度梯度，其等值线(虚线所示)也由“W”型变成“π”型.等温线(点划线所示)在自由表面附近区域向上底面弯曲，此时熔体对流由二维轴对称流动转变为三维稳态非轴对称流动，其周向波数m=4，如图4(b)所示.

图4 无磁场时中截面z=L/2速度(m/s)分布图Fig.4 Velocity(m/s)distribution on z=L/2 section without magnetic fi eld

由图3(c)可见当溶质毛细力和热毛细力共同作用时，其液桥内对流结构与图3(b)中所示热毛细力单独作用时的对流结构相近，此时对流涡心较热毛细对流的涡心略有下移，所不同的是在液桥中心部区域形成了完整的逆向回流涡.此逆向回流涡结构在图 3(a)所示的仅有溶质毛细力作用下的液桥对流结构中同样存在，因此为溶质毛细对流结构所特有.然而，由监测点P的速度及Si浓度随时间变化曲线 (图 5)可以看出：仅溶质毛细力驱动时，P点的速度很小，溶质毛细对流很弱，因此热毛细对流的强度和耦合毛细对流强度相当.但是在溶质毛细力和热毛细力共同驱动下，熔体对流呈现三维周期振荡模式，由傅里叶频谱分析可知其振荡频率f=0.0292Hz(τ=34.2s).溶质毛细流对表面处浓度影响很大，从图5(b)可见，虽然热毛细对流的强度比溶质毛细流的强度大，但是溶质毛细流驱动下P点的Si浓度比热毛细流下P点的浓度要小很多，耦合后P点浓度介于两者之间并随时间呈周期性变化.图6显示了中截面z=L/2上Si浓度在一个周期内的振荡图样，其周向波数m=4，与热毛细对流的周向波数相同.由此可见，即使是弱的溶质对流也会引起热毛细对流稳定性的大幅变化，使稳态的对流转变为周期性振荡流，这一点可以从文献[20-21]的结论得以验证，但与文献[38]的结论不同，他们认为当热毛细对流与溶质毛细对流耦合时，对流的稳定性反而比仅有溶质毛细对流的稳定性要高.

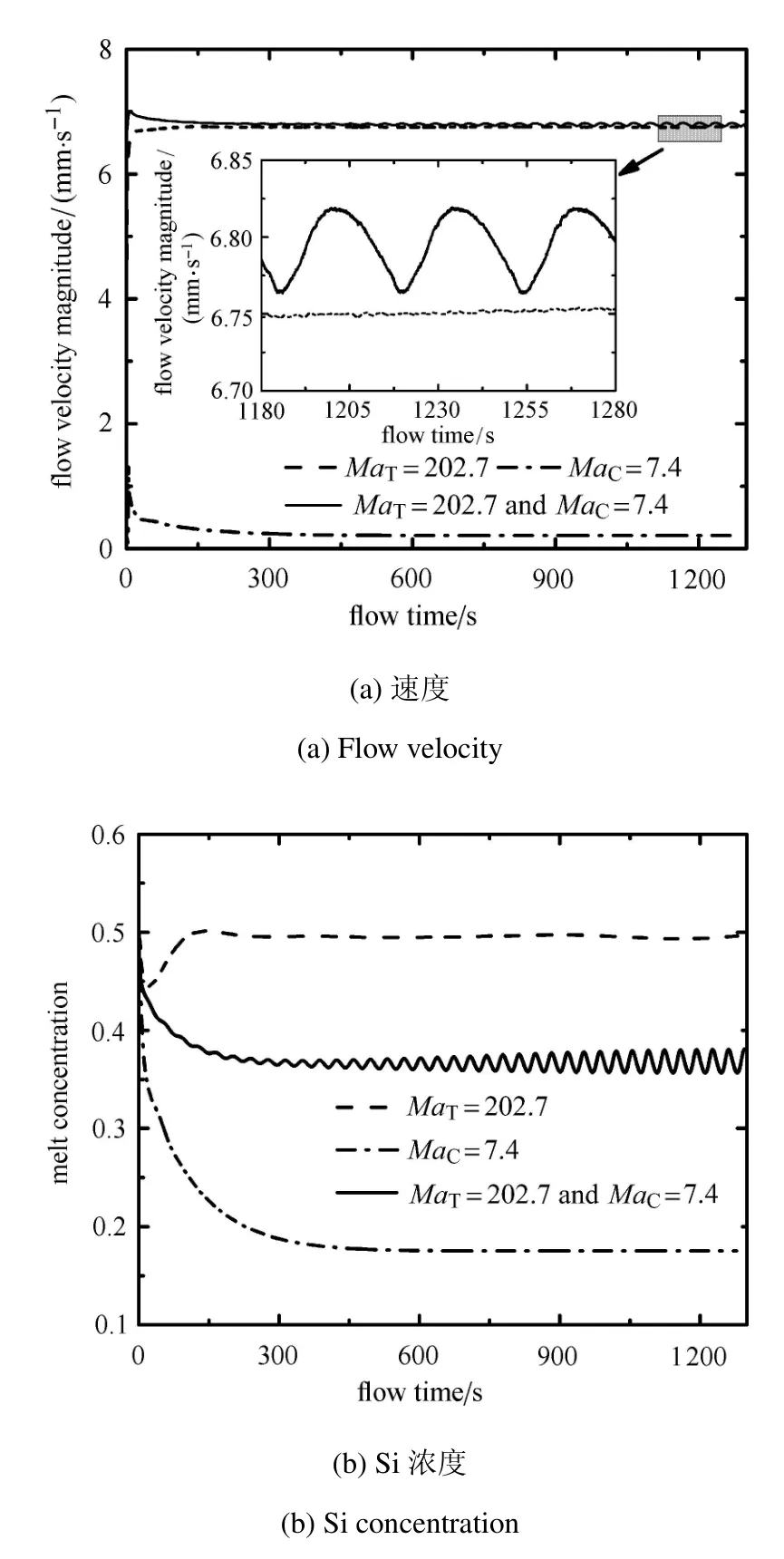
图5 无磁场时监测点P的速度及Si浓度随时间变化曲线Fig.5 Curves of velocity and Si concentration of point P with time without magnetic fi eld

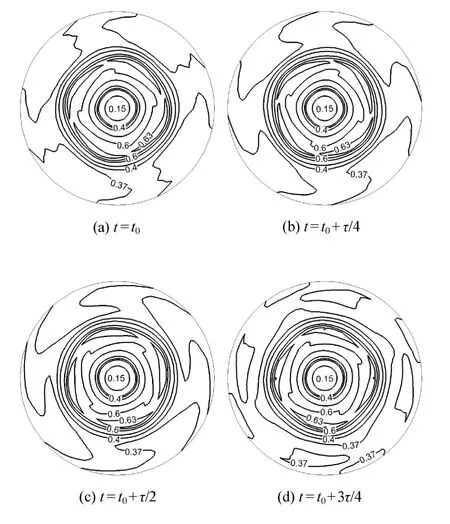
图6 溶质与热毛细力共同作用时中截面z=L/2上Si浓度周期性振荡图Fig.6 Periodic oscillation of Si concentration on z=L/2 section under the e ff ect of coupled solute and thermo-capillary force without magnetic fi eld

对文献[20-21,38]中截然不同的论述，我们更倾向于认同文献[20-21]的结果.就本文而言，溶质毛细对流和热毛细对流都是沿自由表面从下底面向上底面流动，它们耦合时流动是加强的.分析监测点P的数据可知，熔体仅由溶质毛细力驱动时的速度V1=0.21mm/s，对应溶质MaC=7.4；仅由热毛细力驱动时的速度V2=6.75mm/s，对应热MaT=202.7，两者速度之比V2/V1=32.这是由于热毛细力比溶质毛细力要大得多，两者马兰哥尼数之比MaT/MaC=27.因而，当两种不同形式的对流叠加时，流动稳定性发生变化，速度呈现小幅振荡模式.熔体内的浓度则发生较大幅度的振荡.前文已经分析，溶质热毛细对流的涡心在熔体的下半部，所以处在中截面上监测点P的浓度受下半部低浓度的熔体影响较大，C1=0.175；而纯热毛细对流的涡心在熔体的上半部，导致监测点P受上半部影响大，C2=0.495.当两种对流耦合时，高、低浓度的熔体相混合，不稳定性增加，浓度产生较大的振荡，振荡频率和速度振荡频率相同，其峰谷值为0.024.

3.2 旋转磁场对熔区内毛细对流的影响

通过以上分析可知，熔区内流场结构对于溶质Si的输运过程有直接而强烈的影响，因此均匀合理的流场结构有利于改善Si浓度分布的均匀性.在熔区内施加旋转磁场，可以激发熔体运动产生强迫对流.旋转磁场可以对熔体产生与磁场旋转方向相同的周向搅拌作用，适当调节旋转磁场的磁场强度，可以使该强迫对流成为熔体内的主导运动，从而在晶体生长过程中对传热传质有较好的控制.

图7显示，选取的不同磁泰勒数(Ta在7500∼17500之间)时子午面上的流动状态均呈轴对称分布，这是由于旋转磁场产生的洛伦兹力对熔体搅拌作用的结果.从计算结果看，其温度等值线为一系列平行线，此时熔体内对流结构与无磁场时各毛细力驱动的对流结构均不同.原来在液桥中心部区域的逆向回流涡被挤压到液桥下部，并且随着磁场的增加，因回流而削弱的表面毛细对流的程度更大，这样在子午面上的4个顶点附近各形成一个对流涡胞，并且上下两对对流涡胞关于z轴对称.在对流作用下，除表面附近外，熔体中大部分区域Si浓度的等值线走向基本和流线一致，这样，液桥上部分Si浓度较大的熔体向中截面方向流动，液桥下部分Si浓度较低的熔体也向中截面方向流动，因此在中截面附近形成较大的浓度梯度.

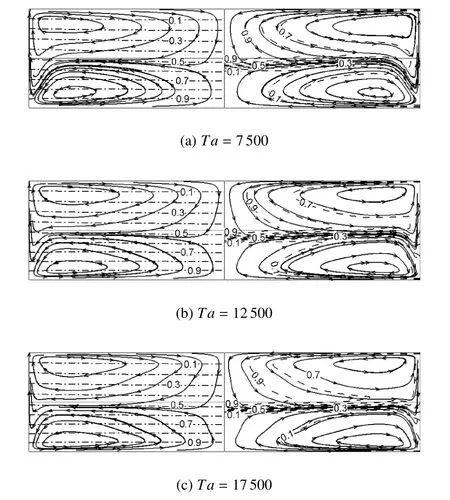
图7 旋转磁场下子午面上流线(实线)、无量纲温度(T*)(左边点划线)和Si浓度(右边虚线)分布图Fig.7 Streamline(solid line),dimensionless temperature(T*)(dash-dot line in the left)and Si concentration(dashed line in the right)distribution on the meridian plane with rotating magnetic fi eld

图8 不同磁泰勒数下中截面z=L/2速度(m/s)等值线图Fig.8 Velocity(m/s)contour lines on z=L/2 section under di ff erent magnetic Taylor numbers

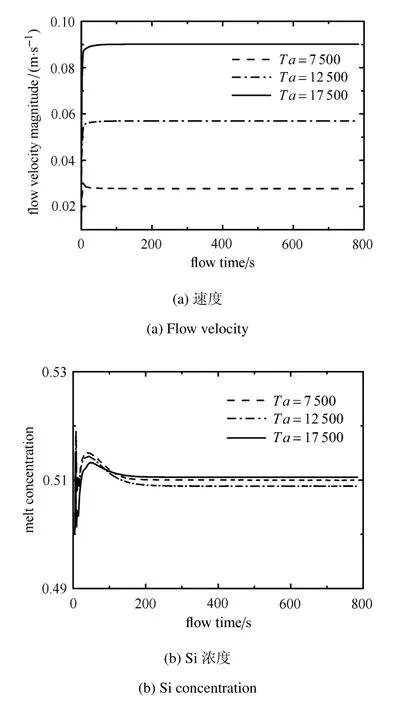
图9 不同磁泰勒数下监测点P的速度及Si浓度随时间变化曲线Fig.9 Curves of velocity and Si concentration of point P with time under di ff erent magnetic Taylor numbers

图8速度分布显示周向波被完全抑制，在旋转磁场洛伦兹力的搅拌下，周向速度关于液桥的中心轴对称，其大小沿径向向外增大并在自由表面处达到最大值.图9显示监测点P的速度及浓度振荡特征已经消失，由此可见，施加3mT(对应Ta=7500)的旋转磁场所产生的强迫对流已经成为熔体内的主导运动，从而熔体由三维振荡流转变为二维轴对称流动；增大磁场强度，监测点P的速度随磁泰勒数近似线性增大.当B0=7mT(Ta=17500)时，测得P的速度为9cm/s，这和Dold等[28]施加7.5mT旋转磁场生长硅单晶时得到的实验数据一致，只是由于SixGe1−x熔体的物性参数不同于Si熔体的物性参数，这一速度略小于文献[28]得到的速度值11cm/s.虽然监测点P点的速度变化很大，但是该处的Si浓度基本相同，并且和纯热毛细流下P点的浓度差别不大.

图10显示中截面z=L/2上Si浓度也呈中心对称分布，浓度等值线呈环状结构，Si浓度周向分布的不均匀性被完全消除，表明旋转磁场的作用可使浓度呈现轴对称分布的特点.在自由表面附近，由于表面张力流的作用，使得下方的Si浓度低的熔体向上方输运，所以中截面上的边缘处Si浓度最小.从图11中截面上Si浓度随径向变化曲线可以看出，浓度从中心处沿径向向外逐渐降低，但在r/R=0.95处出现一个峰值.结合图7不难发现，由于受到液桥下部逆向回流涡的挤压，毛细对流涡胞的流线在r/R=0.90附近突然向下，然后出现一个峰值.在峰值两侧，轴向速度的方向经历了突变，沿半径增加的方向，轴向速度由原来的负向变为正向，原本中截面上方Si浓度高的熔体向下输运变为下方Si浓度低的熔体向上输运，因此在中截面上r/R=0.95处Si浓度出现一个峰值.对比不同磁泰勒数下中截面上Si浓度沿径向变化曲线，我们发现Ta=17500时的浓度曲线较为平坦些，因此，针对文中设定的晶体生长条件，施加7mT(Ta=17500)的旋转磁场可以对传质进行更好的控制.

图10 不同磁泰勒数下中截面z=L/2上Si浓度分布Fig.10 Si concentration contour lines on z=L/2 section under di ff erent magnetic Taylor numbers

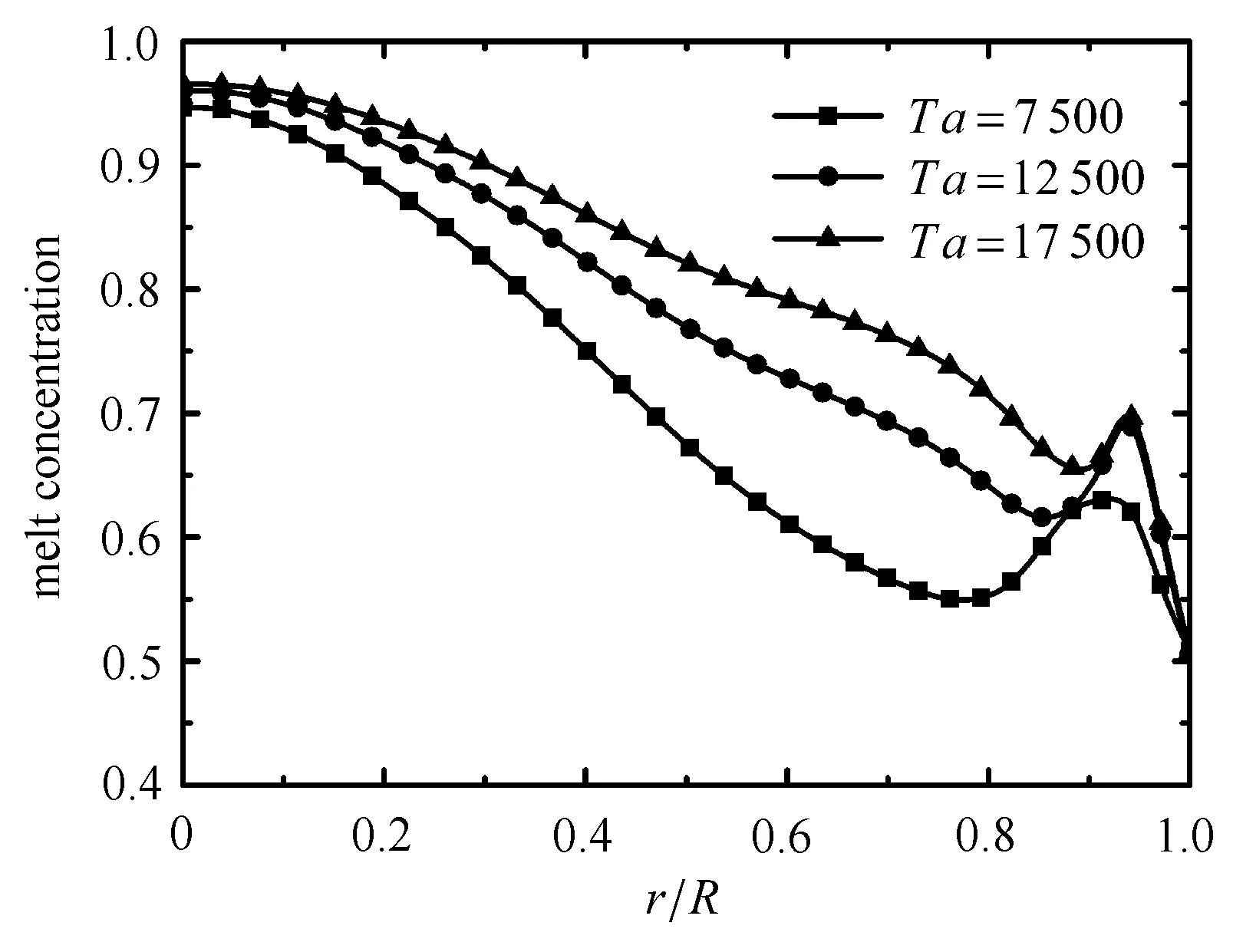
图11 不同磁泰勒数下中截面z=L/2上Si浓度随径向变化曲线Fig.11 Si concentration on z=L/2 section versus radial direction curves under di ff erent magnetic Taylor numbers

4 结论

本文采用半浮区液桥模型，用数值方法研究了溶质毛细对流及热毛细对流的流动特征，并分析了旋转磁场对耦合溶质--热毛细对流流场及浓度场的影响.得到以下结论：

(1)仅受溶质毛细力作用时，熔体在自由表面附近形成低浓度区域，熔体中部区域浓度由扩散和对流共同支配，子午面上浓度等值线呈“W”型；温度场主要由扩散作用决定，呈轴对称分布；溶质毛细对流为二维轴对称流.

(2)在纯热毛细力作用下，熔体内浓度场受热毛细对流的影响很大，浓度分布与熔体内对流流向相关，子午面上浓度等值线呈“π”型分布；温度等值线在自由表面附近区域向上底面弯曲，热毛细对流呈现三维稳态非轴对称流动，其周向波数m=4.

(3)耦合溶质--热毛细对流为三维旋转振荡流，振荡频率f=0.0292Hz，其周向波数与热毛细对流的周向波数相同，m=4.施加旋转磁场后，在洛伦兹力的搅拌下，熔体周向速度沿径向向外增大.在选取的3种不同磁泰勒数(Ta在7500∼17500之间)旋转磁场作用下，熔体内的周向波均被完全抑制，浓度场和流场均呈现二维轴对称分布.因此，施加旋转磁场有助于熔体流动的稳定性和浓度分布、温度分布的均匀性，有利于溶质具有周向对称分布特点的合金晶体的生长.

1 Otani S,Hirata K,Adachi Y,et al.Floating zone growth and magnetic properties of Y2C two-dimensional electride.Journal of Crystal Growth,2016,454:15-18

2 Hossain MM,Watauchi S,Nagao M,et al.E ff ects of growth parameters on silicon molten zone formed by infrared convergent-heating floating zone method.Journal of Crystal Growth,2017,459:105-111

3 Sabanskis A,Surovovs K,Virbulis J.3D modeling of doping from the atmosphere in fl oating zone silicon crystal growth.Journal of Crystal Growth,2017,457:65-71

4 Muiznieks A,Virbulis J,Ldge A,et al.Floating zone growth of silicon//Peter Rudolph ed.Handbook of Crystal Growth(Second Edition).Boston:Elsevier,2015.241-279

5 Da¸bkowska HA,Da¸bkowski AB,Hermann R,et al.Floating zone growth of oxides and metallic alloys//Peter Rudolph ed.Handbook of Crystal Growth(Second Edition).Boston:Elsevier,2015.281-329

6 Lyubimova TP,Skuridyn RV.The in fl uence of vibrations on the stability of thermocapillary flow in liquid zone.International Journal of Heat and Mass Transfer,2014,69(2):191-202

7 Lin K,Dold P,Benz KW,Numerical study of in fl uences of buoyancy and solutal Marangoni convection on flow structures in a germanium-silicon fl oating zone.Crystal Research and Technology,2005,40(6):550-556

8 Surovovs K,Muiznieks A,Sabanskis A,et al.Hydrodynamical aspects of the fl oating zone silicon crystal growth process.Journal of Crystal Growth,2014,401:120-123

9 Capper P,Zharikov E.Oscillatory-driven fluid flow control during crystal growth from the melt//Peter Rudolph ed.Handbook of Crystal Growth(Second Edition).Boston:Elsevier,2015.951-993

10 Tsukada T.The role of marangoni convection in crystal Growth//Peter Rudolph ed.Handbook of Crystal Growth(Second Edition).Boston:Elsevier,2015.871-907

11 Schwabe D,Benz S.Thermocapillary flow instabilities in an annulus under microgravity—results of the experiment magia.Advances in Space Research,2002,29:629-638

12 Schwabe D,Cramer A,Schneider J,et al.Experiments on the multiroll-structure of thermocapillary fl ow in side-heated thin liquid layers.Advances in Space Research,1999,24:1367-1373

13 Schwabe D,Zebib A,Sim BC.Oscillatory thermocapillary convection in open cylindrical annuli.Part 1.Experiments under microgravity.Journal of Fluid Mechanics,2003,491:239-258

14 Chang CE,Wilcox WR.Inhomogeneities due to thermocapillary flow in floating zone melting.Journal of Crystal Growth,1975,28:8-12

15 Smith MK,Davis SH.Instabilities of dynamic thermocapillary liquid layers:Part 1.Convective instabilities.Journal of Fluid Mechanics,1983,132:119-144

16 Li K,Matsumoto S,Imaishi N,et al.Marangoni fl ow in fl oating half zone of molten tin.International Journal of Heat and Mass Transfer,2015,83:575-585

17 姜欢,段俐,康琦.矩形液池热毛细对流转捩途径研究.力学学报,2015,47(3):422-429(Jiang Huan,Duan Li,Kang Qi.Study on transition to chaos of thermocapillary convection in a rectangular liquid pool.Chinese Journal of Theoretical and Applied Mechanics,2015,47(3):422-429(in Chinese))

18 吴勇强,段俐,李永强等.大普朗特数大液桥浮力--热毛细对流地面实验.力学学报,2012,44(6):981-989(Wu Yongqiang,Duan Li,Li Yongqiang,et al.Ground experiments of bouyant thermocapillary convection of large scale liquid bridge with large Prandtl number.Chinese Journal of Theoretical and Applied Mechanics,2012,44(6):981-989(in Chinese))

19 王佳,吴笛,段俐等.大尺寸液桥热毛细对流失稳性地面实验研究.力学学报,2015,47(2):580-586(Wang Jia,Wu Di,Duan Li,et al.Ground experiments of bouyant thermocapillary convection of large scale liquid bridge with large Prandtl number.Chinese Journal of Theoretical and Applied Mechanics,2015,47(2):580-586(in Chinese))

20 Lyubimova TP,Skuridyn RV.Numerical modelling of threedimensional thermo-and solutocapillary-induced fl ows in a fl oating zone during crystal growth.The European Physical Journal Special Topics,2011,192(1):41-46

21 Lyubimova TP,Skuridin RV,Faizrakhmanova IS.Thermo-and soluto-capillary convection in the fl oating zone process in zero gravity conditions.Journal of Crystal Growth,2007,303:274-278

22 Minakuchi H,Okano Y,Dost S.A three-dimensional numerical simulation study of the Marangoni convection occurring in the crystal growthofSixGe1−xbythe fl oat-zonetechniqueinzerogravity.Journal of Crystal Growth,2004,266:140-144

23 游仁然,胡文瑞.浮区中热和溶质的毛细对流.半导体学报,1992,13(4):209-216(You Renran,Hu Wenrui.Analysis of thermo-solutal-capillary convection in fl oating zone.Chinese Journal of Semiconductors,1992,13(4):209-216(in Chinese))

24 Zhou XM,Huai XL.Free surface deformation of thermosolutocapillary convection in axisymmetric liquid bridge.Microgravity Science and Technology,2015,27(1):39-47

25 Robertson GD,Oconnor JD.Magnetic fi eld e ff ects on fl oat-zone Si crystal growth:Strong axial fi elds.Journal of Crystal Growth,1986,72:110-122

26 Hirata H,Hoshikawa K,Silicon crystal growth in a cusp magnetic field.Journal of Crystal Growth,1989,96:747-755

27 邹勇,张银,唐硕捷等.微重力下静态磁场对浮区法硅单晶生长的影响.人工晶体学报,2015,44(9):2343-2349(Zou Yong,Zhang Yin,Tang Shuojie,et al.E ff ect of static magnetic fi elds on growth of fl oating-zone silicon single crystal under microgravity.Journal of Synthetic Crystals,2015,44(9):2343-2349(in Chinese))

28 Dold P,Cröll A,Lichtensteige M,et al.Floating zone growth of silicon in magnetic fi elds:IV.Rotating magnetic fi elds.Journal of Crystal Growth,2001,231:95-106

29 YaoL,ZengZ,LiX,etal.E ff ectsofrotatingmagnetic fi eldsonthermocapillary fl ow in a fl oating half-zone.Journal of Crystal Growth,2011,316:177-184

30 Grants I,Gerbeth G.The suppression of temperature fl uctuations by a rotating magnetic fi eld in a high aspect ratio Czochralski con fi guration.Journal of Crystal Growth,2007,308:290-296

31 Zhou X,Huang H.Numerical simulation of Cz crystal growth in rotating magnetic fi eld with crystal and crucible rotations.Journal of Crystal Growth,2012,340:166-170

32 Yildiz E,Dost S.A numerical simulation study for the combined e ff ect of static and rotating magnetic fi elds in liquid phase di ff usion growth of SiGe.Journal of Crystal Growth,2007,303:279-283

33 Wang L,Shen J,Shang Z,et al.Preparation of gradient material in Sn-Cd peritectic alloy using rotating magnetic fi eld.Journal of Crystal Growth,2013,375:32-38

34 Campbell TA,Schweizer M,Dold P,et al.Float zone growth and characterization of Ge1−xSix(x6 10 at%)single crystals.Journal of Crystal Growth,2001,226:231-239

35 Rakoczy R.Enhancement of solid dissolution process under the influence of rotating magnetic fi eld.Chemical Engineering and Processing:Process Intensi fi cation,2010,49(1):42-50

36 AbbasogluS,SezaiI.Three-dimensionalmodellingofmelt fl owand segregation during Czochralski growth of GexSi1−xsingle crystals.International Journal of Thermal Sciences,2007,46:561-572

37 Levenstam M,Amberg G.Hydrodynamical instabilities of thermocapillary fl ow in a half-zone.Journal of Fluid Mechanics,1995,297:357-372

38 Minakuchi H,Takagi Y,Okano Y,et al.The relative contributions of thermo-solutal Marangoni convections on fl ow patterns in a liquid bridge.Journal of Crystal Growth,2014,385:61-65

INSTABILITY OF COUPLED THERMO-SOLUTE CAPILLARY CONVECTION IN LIQUID BRIDGE AND CONTROL BY ROTATING MAGNETIC FIELD1)

Zou Yong*,†Zhu Guiping*Li Lai*Huang Hulin*,2)
*(College of Energy and Power Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing210016，China)
†(School of Mathematics and Physics，Anhui University of Technology，Ma’anshan243032，Anhui，China)

Floating zone method is an important technology for growth of high-integrity and high-uniformity single crystal materials due to its free of crucible contamination.However,the capillary convection in the melt brings a great challenge to the fl oating zone crystal growth.This is because the instability of convection will cause the formation of some crystal defects such as microscopic imperfections and macroscopic stripes.Therefore,it is very important to investigate the behaviors of the capillary fl ow and control its instability in order to improve the quality of the produced single crystal materials.In this paper,numerical simulations are performed to investigate all kind of the capillary convection in the half floating liquid bridge on the SixGe1−xsystem.And the impact of the external rotating magnetic fi eld is also investigated on the stability of capillary convection.The results show that the purely solute capillary convection is a two-dimensional axisymmetric model，and the temperature fi eld is mainly determined by thermal di ff usion while the concentration fi eld is dominated by convection and solute di ff usion together.On the other hand,the purely thermo-capillary convection presents three-dimensional unsteady axisymmetric fl ow.The concentration distribution is closely related to the fl ow direction of thermo-capillary convection.The isotherms bend in the region with strong convection.The coupled solute and thermocapillary convection is a three-dimensional periodic rotating oscillatory fl ow.When the rotating magnetic fi eld is applied,the circumferential velocity of the melt increases with increasing radius.Both the concentration fi eld and the fl ow fi eld in the melt show a two-dimensional axisymmetric distribution.

fl oating zone，capillary convection，surface tension，numerical simulation，rotating magnetic fi eld

O363.2,O782+.6

A doi：10.6052/0459-1879-17-102

2017–03–27 收稿，2017–09–26 录用,2017–09–26 网络版发表.

1)国家自然科学基金(51276089)、江苏省“六大人才高峰”(2015-XNY-003)和安徽工业大学青年基金(QZ201517)资助项目.

2)黄护林，教授，博士，主要研究方向：磁流体流动与传热.E-mail:hlhuang@nuaa.edu.cn

邹勇,朱桂平,李来,黄护林.液桥内热质耦合对流不稳定性及旋转磁场法控制.力学学报,2017,49(6):1280-1289

Zou Yong,Zhu Guiping,Li Lai,Huang Hulin.Instability of coupled thermo-solute capillary convection in liquid bridge and control by rotating magnetic fi eld.Chinese Journal of Theoretical and Applied Mechanics,2017,49(6):1280-1289