翼伞-载荷系统的航迹跟踪

窦天恒，程文科，高普云

（国防科技大学 航天科学与工程学院，湖南 长沙 410073）

翼伞-载荷系统的航迹跟踪

窦天恒，程文科，高普云

（国防科技大学 航天科学与工程学院，湖南 长沙 410073）

翼伞-载荷系统可被用于精确空投、定点无损着陆以及大型航天器的回收，在航空航天、军事等领域发挥着非常重要的作用。因此，基于翼伞-载荷系统的八自由度动力学模型，采用横向非线性控制方法，对翼伞-载荷系统的航迹跟踪进行了理论分析与仿真模拟。仿真结果表明，飞行器与参考点之间的较佳距离L1为100 m；该距离内，无风和受到5 m/s常值风情况下，所提出的翼伞-载荷系统均能较好地完成90°, 180°,270°, 360°转弯的航迹跟踪，说明横向非线性控制方法具有较好的控制性能和一定的抗风能力，可被应用于翼伞-载荷系统的航迹跟踪控制，为翼伞-载荷系统的优化设计以及大型航天器回收的精确控制提供参考。

翼伞-载荷系统；横向非线性控制方法；航迹跟踪

0 引言

进入21世纪以来，随着科学技术的迅猛发展和新军事变革的不断深入，航空航天和军事领域对精确空投和无损定点着陆技术的要求越来越高。翼伞-载荷系统可被用于精确空投和大型航天器的回收，应用前景广阔，逐渐成为空投和回收领域的研究热点[1]。

翼伞-载荷系统是一个复杂的非线性控制系统，在进行助推器等大型载荷的回收时，由于载荷较大，为了避免系统失稳，需要考虑载荷与伞体之间的相对运动。目前，国内对翼伞-载荷系统的控制研究主要基于六自由度的动力学模型。因此，为了实现对翼伞-载荷系统的精确控制，有必要建立八自由度动力学模型，并在此基础上研究翼伞-载荷系统的控制及航迹跟踪方案。

1 翼伞-载荷系统的八自由度动力学模型

在进行助推器等大型载荷的回收时，为了避免翼伞-载荷系统失稳，需要考虑载荷和伞体之间的相对运动，建立至少二体的动力学方程。当前国内对翼伞控制方面的研究主要基于六自由度模型[2]，即将伞体和载荷看作刚性连接的整体，不考虑两者之间的相对运动。而在实际应用中，伞体与载荷之间是存在相对运动的，显然，基于六自由度的控制方法研究已经不能满足实际应用的需求。因此，本研究使用的模型为翼伞-载荷系统的八自由度刚性铰接模型[3]，即在六自由度模型[4-6]的基础上，考虑了载荷相对于伞体的两个相对转动自由度[7]，即相对偏航和相对俯仰。

2 翼伞-载荷系统的跟踪控制

翼伞-载荷系统不同于固定翼飞机或旋翼飞行器，其横向控制只能通过左右后缘下拉来实现，且操纵具有一定的迟滞性[8]，因此，可以将导弹制导中的横向非线性制导方法用于翼伞-载荷系统的跟踪控制。

2.1 横向非线性控制方法的原理

横向非线性控制方法[9-10]的原理是在期望轨迹上选取一系列的航迹点，控制飞行器在这一系列航迹点上飞行，即可跟踪一条给定的路径。每计算1次，都要在期望轨迹上距离翼伞L1的位置上选择一个参考点，如图1所示。

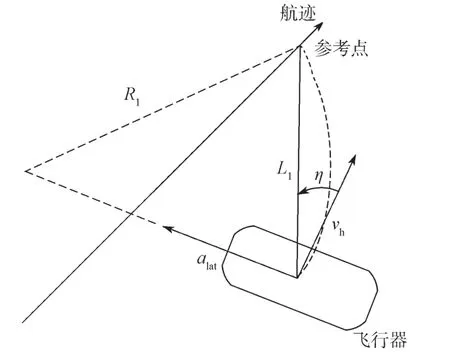
图 1 横向非线性控制方法原理图Fig. 1 A schematic diagram of the lateral non-linear control method

选取的参考点与翼伞的连线和翼伞水平速度vh之间的夹角用η表示，则产生的横向加速度的表达式为

如果选取的参考点位于飞行器速度矢量的左侧，则横向加速度方向向左；反之，如果选取的参考点位于飞行器速度矢量的右侧，则横向加速度方向向右。当飞行器的速度方向刚好指向参考点时，横向加速度为0。因此，在横向加速度的作用下，飞行器将沿圆周从当前位置向参考点运动，如图1中虚线所示。圆周运动的半径R1为

通过这种横向非线性控制方法，可以实现对飞行器的航迹跟踪。

2.2 参考点选取对跟踪控制的影响

在横向非线性控制方法中，参考点的选取非常关键，其用飞行器当前位置到参考点的距离L1表示。横向非线性控制方法的原理就是控制飞行器的速度方向指向参考点，因此，L1的选取至关重要，下面分析L1对跟踪控制的影响，图2为参考点对跟踪控制的影响示意图。

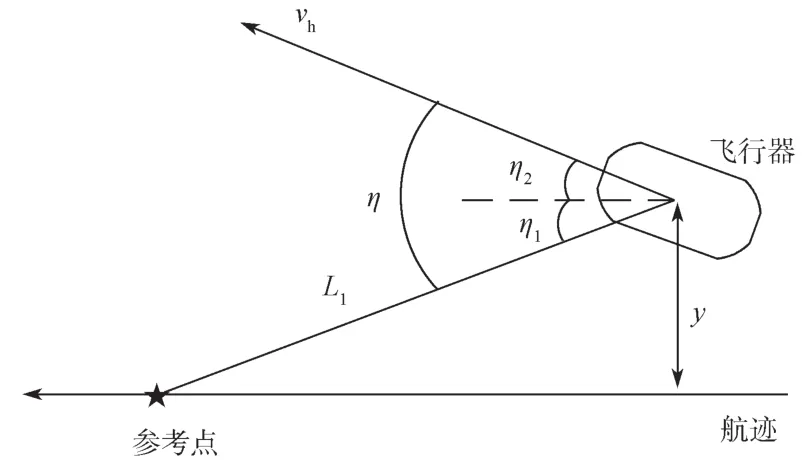
图 2 参考点对跟踪控制的影响示意图Fig. 2 In fl uence of reference point on tracking control

如图2所示，L1为飞行器与参考点之间的距离，y为横向轨迹偏差，vh为飞行器当前的速度，η1，η2为飞行器的横向偏差。假设η很小，则有

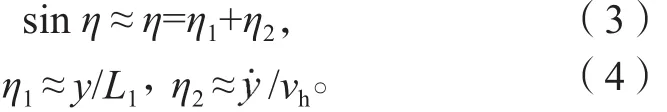
将式（3）（4）代入式（1）可得

由式（5）可知，飞行器与参考点之间的距离L1是影响控制器增益的重要因素：如果L1取值过小，飞行器运动的向心加速度过大，可能会使系统失稳；如果L1取值过大，飞行器运动的向心加速度过小，则会使系统响应较慢，跟踪时间较长。

2.3 翼伞-载荷系统的航迹跟踪

在翼伞-载荷系统受控进行横向加速的过程中，假设其沿一条圆弧轨迹运动，该轨迹由参考点的位置、翼伞-载荷系统的位置以及翼伞载荷系统的速度方向决定[9]。该圆弧轨迹从翼伞-载荷系统当前位置开始，与速度方向相切，在参考点处结束。这样，翼伞-载荷系统的横向加速度就等于该段圆弧轨迹的向心加速度。由式（2）可得该圆弧轨迹的曲率半径为

由此可得，其向心加速度为

翼伞-载荷系统沿圆弧运动的角速度为

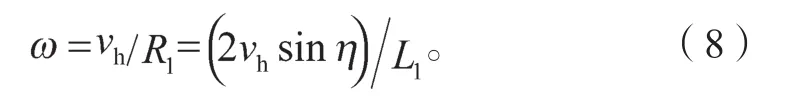
式中ω为翼伞-载荷系统的偏航角速度，即转弯速率。

翼伞-载荷系统的横向控制只能通过左右后缘下偏实现，即通过转弯来实现。根据对翼伞-载荷系统转弯特性的分析，得到翼伞-载荷系统不同的单侧后缘下偏量对应的转弯速率和转弯半径[3]，如表1所示。因此，在跟踪期望轨迹的过程中，可以根据横向非线性控制中的角速度即翼伞-载荷系统的转弯速率来确定后缘下偏量的大小。

表 1 单侧下偏量与转弯速率、转弯半径的关系Table1 Relationship between brake de fl ection and turning rates and radius

由表1可以得知，当下偏量δ=5%时，翼伞-载荷系统的转弯速率为0.009 8 rad ·s-1；当下偏量δ=10% 时，其转弯速率为 0.027 5 rad ·s-1。

假设翼伞-载荷系统的下偏量与转弯速率为线性关系，则翼伞-载荷系统的瞬时后缘下偏量可以

式中k为比例系数。

由于翼伞-载荷系统的操纵具有一定的迟滞性，因此，可以通过调节k的大小来适当增加控制量，以克服其迟滞性的影响，同时增强其抗风能力。

此外，由表1还可得知，当下偏量δ=30%时，转弯半径为133 m。由于下偏量过大会导致翼伞-载荷系统失稳，因此，当期望轨迹的曲率半径小于133 m时，认为翼伞-载荷系统只能以最大的转弯速率来跟踪，即取翼伞-载荷系统的最大下偏量δ=30%。

2.4 航迹跟踪的仿真与结果分析

由前面的分析可知，L1取值的大小对航迹跟踪的效果有着重要的影响，下面以跟踪90°转弯航迹为例，仿真翼伞-载荷系统的跟踪效果。

假设翼伞-载荷系统在无风环境下正沿x轴正方向飞行，将L1分别取50, 100, 150, 200, 300, 400 m，比例系数k取3，所得仿真结果如图3所示。

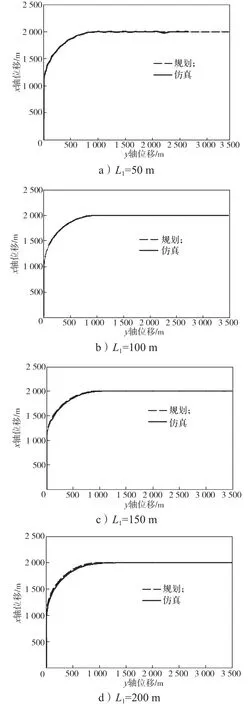
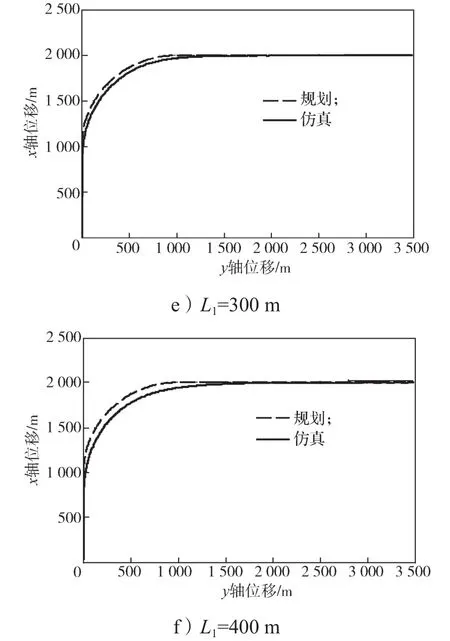
图3 不同L1取值下的航迹跟踪仿真结果Fig. 3 Simulation results of trajectory tracking with different values of L1

由图3可知，当L1取值过小时，控制效果不理想，曲线收敛较快，但后期会有不衰减的微小振荡，如图3a；当L1取值过大时，收敛较慢，控制时间较长，需要足够的距离才能跟踪到指定方向，控制精度较低，如图e、f。可见，所得仿真结果与之前对L1取值的理论分析基本一致。对比图3中各曲线可以得知，当L1=100 m时，控制效果最好。

下面取L1=100 m，分别仿真翼伞-载荷系统在无风情况下跟踪90°, 180°, 270°, 360°转弯的航迹图，所得仿真结果如4所示。

由图4可知，翼伞-载荷系统较好地完成了对各转弯角度的跟踪，达到了预期控制效果，控制精度较高。

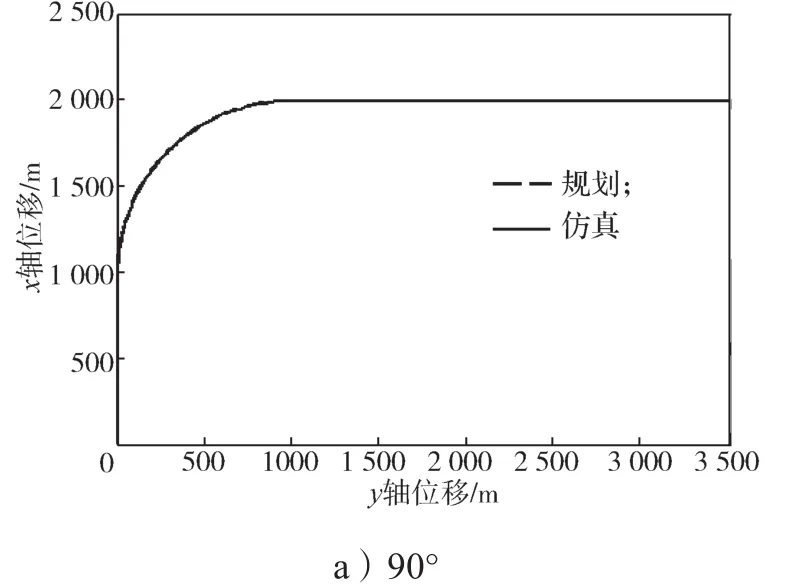
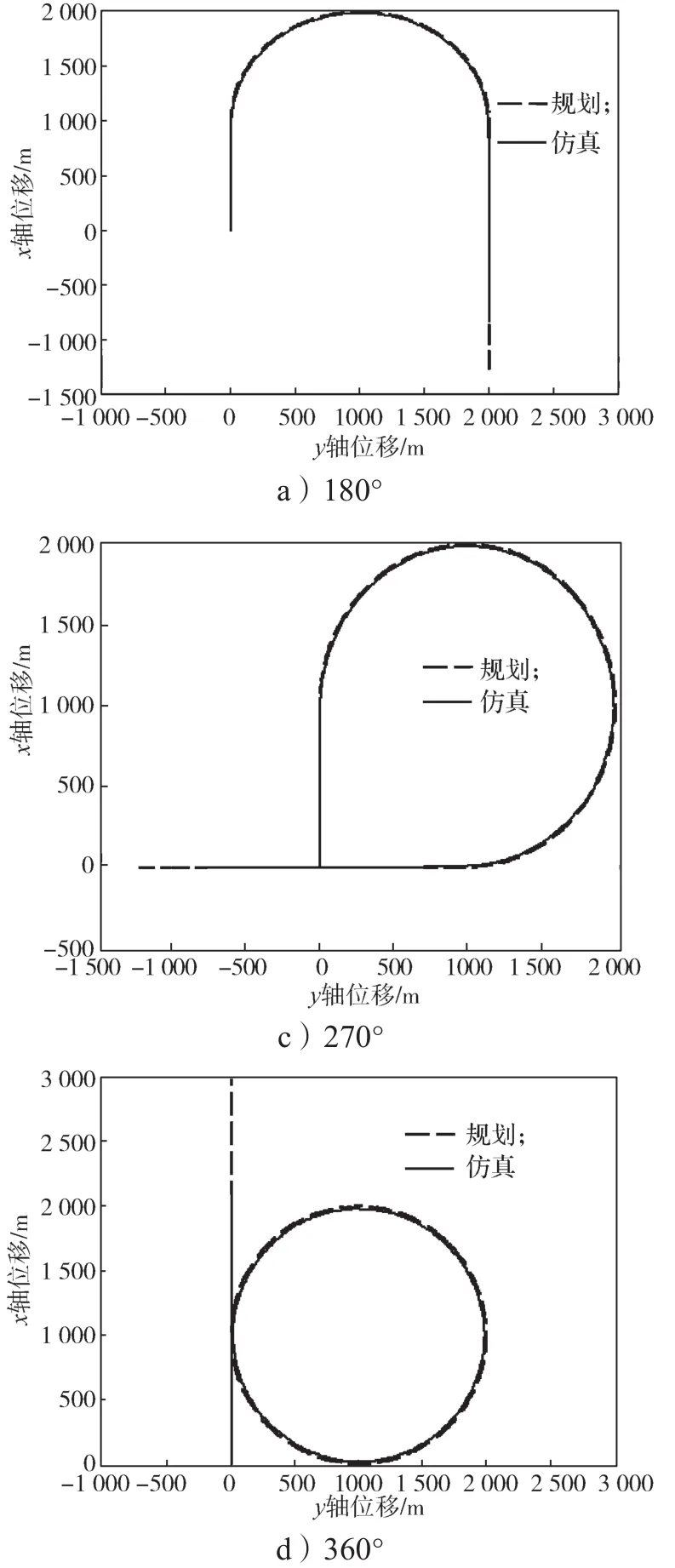
图4 无风下不同转弯角度的航迹跟踪仿真结果Fig. 4 Simulation results of trajectory tracking under different turning angles without wind

为了进一步考察该控制方法的抗风性能，假设翼伞-载荷系统受到5 m/s的常值风，风向沿x轴正方向，其它条件与无风时保持一致。分别仿真翼伞-载荷系统跟踪90°, 180°, 270°, 360°转弯的航迹图，所得仿真结果如图5所示。

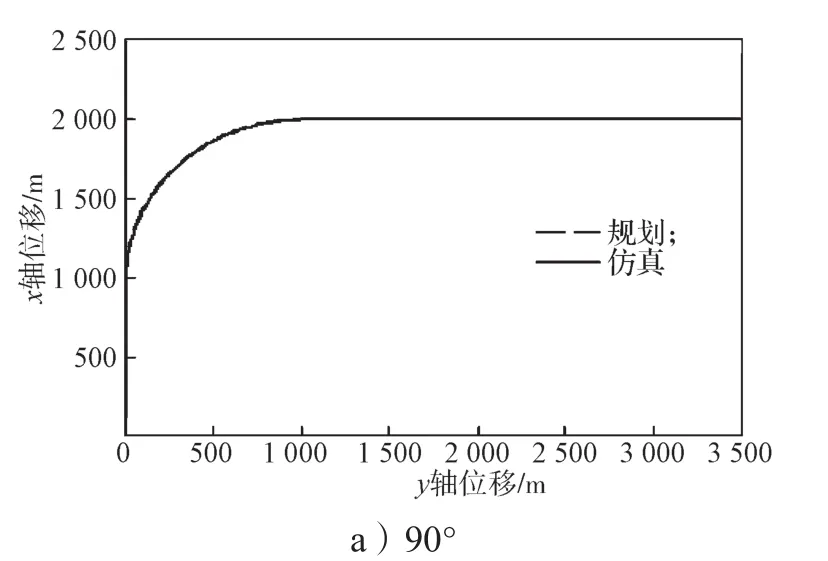
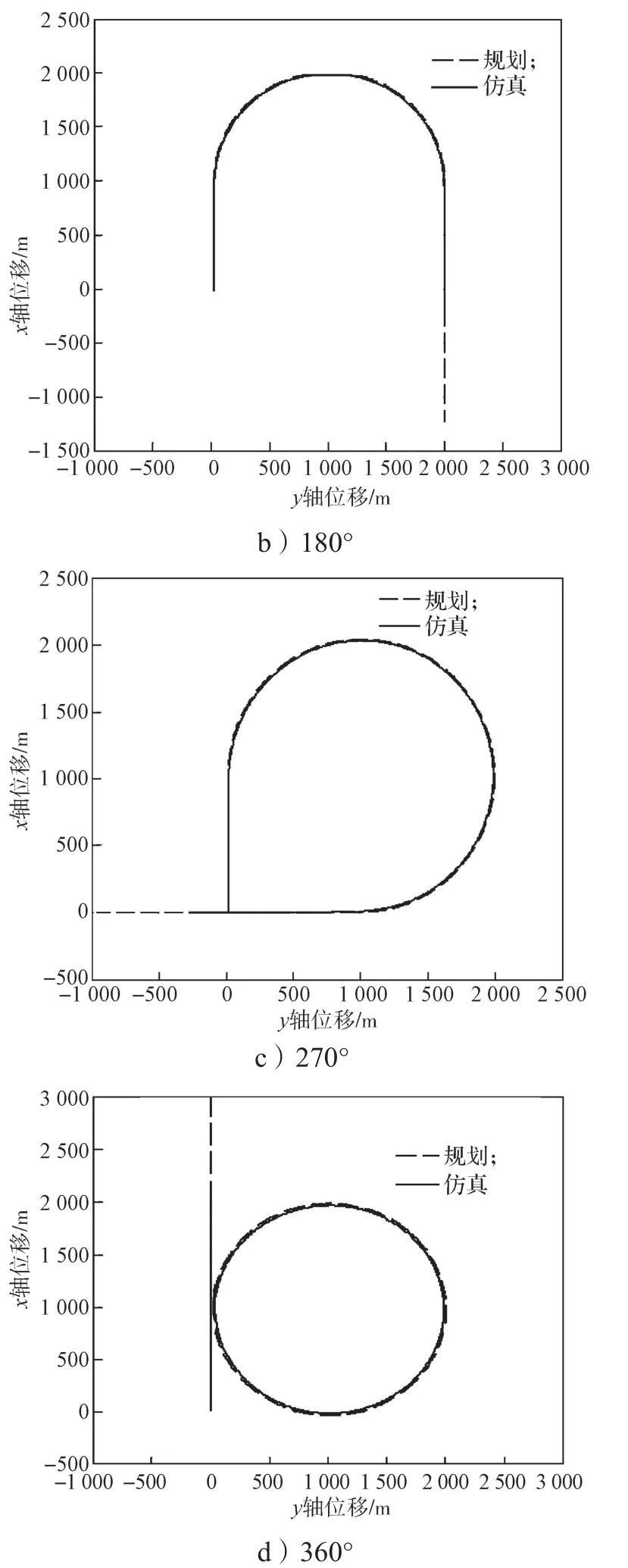
图5 风速为5 m/s时不同转弯角度的航迹跟踪仿真结果Fig. 5 Simulation results of trajectory tracking under different turning angles with a wind of 5 m/s

对比分析图5与图4可知，在无风和受到5 m/s常值风情况下，翼伞-载荷系统的跟踪轨迹差别很小，控制效果基本相同，说明横向非线性控制方法具有一定的抗风能力。但仿真实验过程中发现，当风速达到一定数值后，翼伞-载荷系统不能有效地跟踪航迹。如以360°转弯为例，假设风速为10 m/s，风向沿x轴正方向，其它条件不变，所得仿真跟踪结果如图6所示。由图6可知，当风速达到10 m/s时，翼伞-载荷系统不能有效地跟踪360°转弯航迹，控制过程出现较大偏差，且这种偏差在顺风时尤为明显。

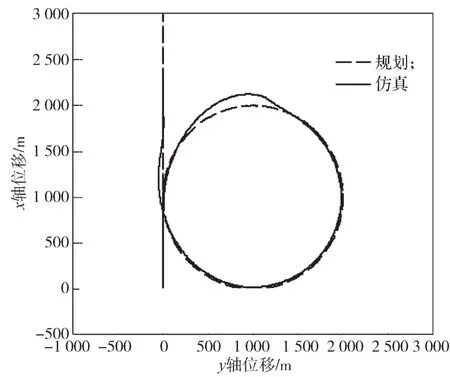
图6 风速为10 m/s时360°转弯航迹跟踪仿真结果Fig. 6 Simulation results of trajectory tracking under a turning angle of 360° with a wind of 10 m/s

翼伞-载荷系统的抗风能力与后缘下偏量的大小有关，式（9）中提到，由于翼伞-载荷系统的迟滞性，适当提高比例系数k可以增大控制量，可在一定程度上提高翼伞-载荷系统的抗风能力。以上仿真过程中k的取值都为3，下面选取k=1，L1=100 m，以360°转弯为例，分别仿真无风和风速为5 m/s常值风情况下翼伞-载荷系统的跟踪情况，所得结果如图7所示。

图7 k=1，L1=100 m时有无风下360°转弯航迹跟踪仿真结果Fig. 7 Simulation results of trajectory tracking undera turning angle of 360°without wind or with k=1 and L1=100

由图7可知，当k=1时，在无风情况下，翼伞-载荷系统360°转弯的航迹跟踪效果与图4d基本相同，可见能较好地完成航迹跟踪；但在风速为5 m/s的常值风影响下，航迹跟踪效果与图5d相差较大，不能有效地完成跟踪。这一结果表明，适当增大k的取值，可以在一定程度上提高翼伞-载荷系统的跟踪精度和抗风能力，仿真结果与此前的理论分析一致。

3 结论

本文基于翼伞-载荷系统的八自由度模型，采用横向非线性控制方法，研究了翼伞-载荷系统的航迹跟踪，通过仿真验证，可得到如下结论：

1）飞行器与参考点之间的距离L1是影响控制器增益的重要因素，其取值大小对航迹跟踪的效果有着重要影响，当L1取值过小时，控制效果不理想，曲线收敛较快，且后期会有不衰减的微小振荡；当L1取值过大时，收敛较慢，控制时间较长，需要足够的距离才能跟踪到指定方向，控制精度较低，所设定的取值范围内，当L1=100时，控制效果最好。

2）所提出的横向非线性控制方法较好地完成了对90°, 180°, 270°, 360°转弯的航迹跟踪，达到了预期控制效果，控制精度较高。

3）在无风和受到5 m/s常值风情况下，翼伞-载荷系统的跟踪轨迹差别很小，控制效果基本相同，说明横向非线性控制方法具有一定的抗风能力。但当风速达到一定程度后，如10 m/s，翼伞-载荷系统不能有效地跟踪航迹。

4）适当增大k的取值，可以在一定程度上提高翼伞-载荷系统的跟踪精度和抗风能力。

以上结论表明，所提出的翼伞-载荷系统能较好地完成各转弯的航迹跟踪，说明横向非线性控制方法具有较好的控制性能和一定的抗风能力，能够应用于翼伞-载荷系统的航迹跟踪控制，为实现翼伞-载荷系统的精确稳定控制提供了理论方法。

[1] 宋旭民，程文科，彭 勇，等. 先进的精确空投系统[J].航天返回与遥感，2004，25(1)：6-10.SONG Xumin，CHENG Wenke，PENG Yong，et al. Advanced Precision Airborne Delivery Systems[J].Spacecraft Recovery and Remote Sensing，2004，25(1)：6-10.

[2] 熊 菁. 翼伞系统动力学与归航方案研究[D]. 长沙：国防科技大学，2005.XIONG Jing. Research on the Dynamics and Homing Project of Parafoil System[D]. Changsha：National University of Defense Technology，2005.

[3] 窦天恒，程文科. 翼伞-载荷系统的建模和运动特性分析[C]//第五届全国航天飞行动力学技术研讨会论文集. 文昌：航天飞行动力学技术重点实验室，2017：154-164.DOU Tianheng，CHENG Wenke. Modeling and Motion Characteristic Analysis of the Parafoil-Payload System[C]//The 5th National Symposium on Space Flight Dynamics. Wenchang：The Key Laboratory of Space Flight Dynamics，2017：154-164.

[4] 胡文治，陈建平，张红英，等. 翼伞空投系统的动力学建模与飞行控制仿真[J]. 航空计算技术，2017，47(3)：70-73.HU Wenzhi，CHEN Jianping，ZHANG Hongying，et al. Dynamics Modeling and Flight Control Simulation of Parafoil Aerial Delivery Systems[J]. Aeronautical Computing Technique，2017，47(3)：70-73.

[5] 周 靓，戈嗣诚，张青斌，等. 翼伞空投系统动力学建模与仿真[J]. 航天返回与遥感，2017，38(2)：10-16.ZHOU Liang，GE Sicheng，ZHANG Qingbin，et al.Dynamic Modeling and Simulation of Parafoil Airdrop System’s[J]. Spacecraft Recovery and Remote Sensing，2017，38(2)：10-16.

[6] 蒋万松，荣 伟. 火箭助推器翼伞回收动力学仿真分析[J]. 兵器装备工程学报，2017，38(3)：6-13.JIANG Wansong，RONG Wei. Dynamical Simulation Analysis for Booster Recovery with Parafoil System[J].Journal of Weapon and Equipment Engineering，2017，38(3)：6-13.

[7] 熊 菁，宋旭民，秦子增. 翼伞系统两体相对运动分析[J]. 航天返回与遥感，2004，25(2)：10-16.XIONG Jing，SONG Xumin，QIN Zizeng. Analysis on Two Body Relative Movement of Parafoil System[J].Spacecraft Recovery and Remote Sensing，2004，25(2)：10-16.

[8] MÜLLER S，WANGER O，SACHS G. A High-Fidelity Nonlinear Multibody Simulation Model for Parafoil Systems[C]// 17th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar.California：[s. n.]，2003：325-334.

[9] GIDEON V D K. Flight Control System for an Autonomous Parafoil[D]. Stellenbosch：Stellenbosch University，2013.

[10] WATANABE M，OCHI Y. Modeling of Nonlinear Dynamics of a Powered Paraglider[J]. Journal of the Japan Society for Aeronautical & Space Science，2008，56(658)：499-509.

Research on the Path Tracking of the Parafoil-Payload System

DOU Tianheng，CHENG Wenke，GAO Puyun
（School of Aerospace Science and Engineering，National University of Defense Technology，Changsha 410073，China）

The parafoil-payload system, which plays an important role in such fi elds as aerospace and military affairs, can be applied for precision airdrop, nondestructive landing and large spacecraft recovery. Therefore, based on 8-DoF dynamic model of the parafoil-payload system, the lateral nonlinear control method has been adopted to analyze and simulate the tracking of the parafoil-payload system. The simulation results show that 100 m will be the optimum distance L1between the vehicle and the reference point, under which condition, the proposed parafoil-payload system can ef fi ciently achieve trajectory tracking under different turning angles of 90°, 180°, 270° and 360° without wind or with a constant wind of 5 m/s. It illustrates that the lateral non-linear control method exhibits a better control performance as well as certain control ability to withstand wind, which can be applied to the trajectory tracking of the parafoil-payload system, thus providing a good reference to the optimization design of the parafoil-payload system and precision control of large spacecraft recovery.

parafoil-payload system；lateral non-linear guidance method；path follower

V448.121；TP391.9

A

1673-9833(2017)05-0011-06

10.3969/j.issn.1673-9833.2017.05.003

2017-08-10

窦天恒（1992-），男，山东青州人，国防科技大学硕士生，主要研究方向为航天器回收，E-mail：dth_1210@163.com

（责任编辑：廖友媛）