三角形问题中避免增解的常用策略

江苏 王安寓 范贤丽

三角形问题中避免增解的常用策略

江苏 王安寓 范贤丽

计算是数学学习中的一种重要技能．数学运算是新课标六大数学核心素养之一．数学运算不仅是数学发展的重要起源，更是数学后续发展思想方法的源泉．数学运算贯穿数学的基本脉络，几乎渗透到数学的每一个角落．三角形问题中离不开计算，但有些三角形问题的计算往往会出现增解，如何避开增解呢？首先，要弄清楚产生增解的原因，然后根据产生增解的原因寻找对应的解决策略．造成解三角形问题的增解的原因，主要有运用同角三角函数的平方关系开方、由正弦值求角的运算、钝角或锐角的充要条件等等．根据增解原因，思考对应的解决策略：少用开方、少用正弦、缩小角的范围、找准钝角或锐角的充要条件等等．

策略一：能用倍角，符号内蕴，不用开方

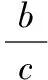
(Ⅰ)求sinB；

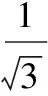
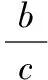
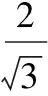
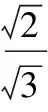
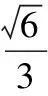
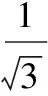
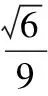
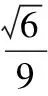
点评：当出现平方关系需要开方时，一定要小心，要判断清楚符号，才能实施开方运算．当题设中存在倍数关系时，要优先选择倍数关系，避开出现开方造成增解．

策略二：能用余弦，或者正切，不用正弦

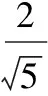
分析：由条件易求sinA, sinB，再由和角公式求C的某一三角函数值．

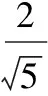
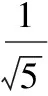
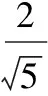
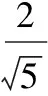
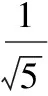
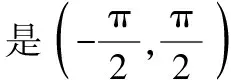
由于是限制在三角形中，角的范围往往是(0,π)，因此，要多求余弦或正切，而少用正弦．

错解：设P(x,y)在第一象限，

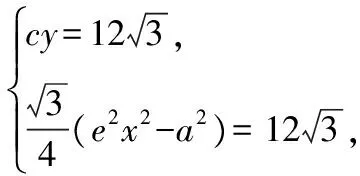
即a4-16a2+48=0，解得a2=4或12，

正解：设P是第一象限的点，设|PE|=m,|PF|=n，则m-n=2a，则余弦定理有

4c2=m2+n2-mn=(m-n)2+mn，∴mn=4b2，

策略三：钝角锐角，充要条件，避开增解

【例4】钝角三角形ABC中，a=1，b=2，则最大边c的范围是________．

分析：最大边所对的角一定为钝角．由cosClt;0求得c的范围．

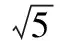
错因分析：显然c不能取很大的值．实际上，c=5gt;a+b，构不成三角形．

在三角形中，一般用余弦定理就能避开增解，为什么本题出现了增解？请先思考：cosClt;0C为钝角吗？也就是说，cosClt;0是C为钝角的必要不充分条件．cosClt;0中还包含cosC=-1！C为钝角lt;Clt;π-1lt;cosClt;0．因此，在附加条件“三角形”下，C为钝角的充要条件是-1lt;cosClt;0．

正解：∵c是最大边，△ABC为钝角三角形，∴C为钝角，∴-1lt;cosClt;0，

点评：在△ABC中，角A为钝角-1lt;cosAlt;0；角A为锐角0lt;cosAlt;1．

锐角三角形ABC

笔者不禁回想起向量夹角为钝角的问题．能借鉴吗？

题目(必修4P85练习5改编)设向量a=(x,4)，b=(-2,-1)，向量a与b的夹角为钝角，则实数x的取值范围是________．

解析：a与b的夹角为钝角a·blt;0且a与b不共线-2x-4lt;0且-x≠-2×4xgt;-2且x≠8．

在处理向量夹角为钝角时，采用剔除法：在a·blt;0中剔除a与b共线，相当于排除a与b的夹角为π(当然也包含0)的情形．这种解法能借鉴到三角形中钝角问题．

如，例4也可以采用向量的解法．

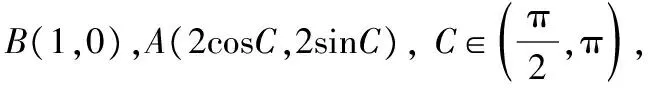
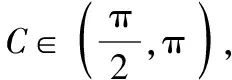
这种解法是最本质的解法．

这启发我们，解三角形问题，完全可以用解析法．

策略四:用已知角，表示待角，避开增解

分析：由题意求角A，用余弦定理求边c．

∴a2=7=32+c2-3c，解得c=1或2．

点评：由正弦定理求边所构建的方程是一次式，其解也唯一．因此，不会出现增解．与策略一比较，应能体会求边与求角的不同处理方式．本题中，“锐角三角形ABC”是指A,B,C都是锐角，不能只看一个角或两个角．本题求边c，也可以用射影定理求解．c=acosB+bcosA=2．

策略五:比较函值，确定角围，避开增解

分析：求出sinB,cosC，运用诱导公式和两角和的正弦公式求解．

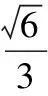
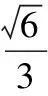
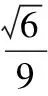
点评：比较正弦值，结合正弦定理，得到边的关系，再根据大角对大边、大边对大角的结论，确定角的范围，是求解某些三角形问题的常用方式．挖掘隐含条件，缩小角的范围，是求解三角形问题必须考虑的．

策略六:二次方程，多解检验，避开增解

(Ⅰ)求角C的大小；

(Ⅱ)若a2=2b2+c2，求tanA的值．

分析：(Ⅰ)根据向量共线得到关于cosC的方程，解方程并注意范围；(Ⅱ)由边的关系联想正弦定理，降次、万能公式或化切，解方程即可．

(Ⅱ)∵a2=2b2+c2,

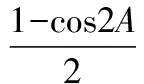
正解1：由余弦定理得c2=a2+b2-ab，

∴a2=2b2+c2=2b2+a2+b2-ab，∴ab=3b2，

∴a=3b，

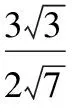
正解2：仿上得a=3b，

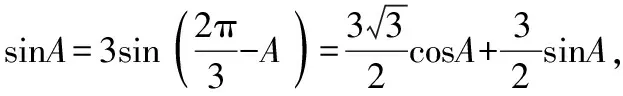
江苏省南京市六合区实验高级中学)