立体几何中向量法求点的坐标的解题策略

湖北 向正银

立体几何中向量法求点的坐标的解题策略

湖北 向正银

利用空间向量求角与距离是高考的一个高频考点，关键是建立空间直角坐标系，在没有明显建系条件的，先要找到两两垂直的三条线，在选择合适的原点建系，有时个别点的坐标不能直接写出来，需要借助向量间的关系来转化；题目已知数据太少无法写坐标，巧设多个参数求解；已知条件线段比中含参数不易写坐标，引入新的参数后再转化.

一、建系后个别点的坐标直接写不出，利用向量间的关系来转化

(Ⅰ)求证：平面BCD⊥平面AB1C；

(Ⅱ)若OC=OA，求直线C1D与平面ABC所成角的正弦值.

所以△BAD∽△AA1B1，则∠AB1B=∠ABD,

∠BAB1+∠ABD=90°,∠BOA=90°,

即BD⊥AB1,又CO⊥平面ABB1A1，

所以CO⊥AB1,又BD∩CO=O,

所以AB1⊥平面BCD，AB1⊂平面AB1C，

所以平面BCD⊥平面AB1C.

(Ⅱ)以为O原点，分别以OD,OB1,OC所在的直线为x轴、y轴、z轴建立空间直角坐标系，

设直线C1D与平面ABC所成的角为

二、题目已知数据太少无法写坐标，巧设多个参数求解

【例2】(2017·武汉市四月高三联考试题)如图，在三棱柱ABC-A1B1C1中，平面A1ACC1⊥平面ABC，AB=BC=2，∠ACB=30°，∠C1CB=120°,BC1⊥A1C.E为AC中点，

(Ⅰ)求证：A1C⊥平面C1EB；

(Ⅱ)求二面角A1-AB-C的余弦值.

解：(Ⅰ)证明略.

又平面A1ACC1⊥平面ABC，AB=BC=2，

E为AC中点，

联立①，②解方程组得

设平面A1AB的一个法向量m=(x,y,z)，

【点评】这道立体几何是一道难题，当时学生的正确率不到1%，因为建系后A1的纵坐标，竖坐标都不知道，标准答案是设|AA1|=t,∠A1AC=θ，通过条件列两个方程，解出参数，写出A1的坐标，使问题解决，实际上直接设A1的坐标，更容易思考和计算.

三、已知条件线段比中含参数不易写坐标，引入新的参数后再转化

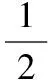
(Ⅰ)求证：平面DPC⊥平面BPC;

【解析】(Ⅰ)证明:如图，取PB中点N，连接MN,AN．

∴四边形ADMN为平行四边形，

∴AD⊥平面PAB，∴AD⊥AN，

∴AN⊥MN，AP=AB，∴AN⊥PB，

∴AN⊥平面PBC．∵AN∥DM，

∴DM⊥平面PBC，即平面DPC⊥平面BPC.

(Ⅱ)存在符合条件的λ.以A为原点，AB方向为x轴的正方向，AD方向为y轴的正方向，AP方向为z轴的正方向，建立如图所示的空间直角坐标系．

设平面PDE的法向量n1=(x,y,z)，

令y=2,则z=2,x=2-t,

取平面PDE的一个法向量为n1=(2-t,2,2)．

平面DEB即为xAy平面，

湖北省兴山县第一中学)