我为高考模考命题——谈概率统计题的命制

新疆 徐 波

我为高考模考命题
——谈概率统计题的命制

新疆 徐 波

概率统计试题在高考试卷中占了一道大题(12分)，历来为兵家(考生)必争之地，概率统计试题的核心是考查考生的数据处理能力，那么，什么是数据处理能力呢？对比2016年和2017年高考考纲后发现,对数据处理能力的要求已经发生了悄然的变化：

2016年高考考纲中对数据处理能力的要求是：

“数据处理能力：会收集、整理、分析数据,能从大量数据中抽取对研究问题有用的信息,并做出判断.

数据处理能力主要依据统计或统计案例中的方法对数据进行整理、分析，并解决给定的实际问题.”

2017年高考考纲中对数据处理能力的要求是：

“数据处理能力：会收集、整理、分析数据,能从大量数据中抽取对研究问题有用的信息,并做出判断.

数据处理能力主要是指针对研究对象的特殊性，选择合理的收集数据的方法，根据问题的具体情况，选择合适的统计方法整理数据，并构建模型对数据进行分析、推断,获得结论.”

对比2016年和2017年高考考纲中对数据处理能力的要求，我们发现：2017年高考考纲中对数据处理能力的要求提高了，如果说2016年考纲对数据处理能力的要求是“会用模型”，那么2017年考纲对数据处理能力的要求就是“根据问题的具体情况，选择合适的统计方法，构建模型对数据进行分析、推断,获得结论.”也就是说对模型的要求提高了.

由于笔者有多年参与乌鲁木齐市高三诊断性测试命题的经历和经验，其中的概率统计题的命制大多是由笔者负责完成的，在对历年高考真题的研究和在乌鲁木齐市高三诊断性测试命题实践中笔者深切体会到用样本估计总体、用样本的频率分布估计总体的概率分布，这是概率统计这门课程的基本思想，而数据处理能力又是解决概率统计题的关键，所以，下面笔者就选择几道我们原创的乌鲁木齐市高三诊断性测试试题来进行举例说明，同时，也想把这些原创的试题介绍给大家共享和交流.

一、含有两个随机变量的题型定式

通过研究历年高考试题，我们发现在一个题目里总是会设置两个随机变量X和Y，其中X是作为已知条件呈现出来的(呈现的方式有频率分布直方图、频率分布表、茎叶图等)，而Y是与X有关联的一个量，Y是X的函数，Y与X的这种函数关系的呈现方式可以是解析式、也可以是表格.Y就是用来出题的，题目当中的问题就是针对Y这个量来出的.这是这些年高考题的一个基本的模式和套路.

【例1】(2014年乌鲁木齐市高三第一次诊断性测试理科第19题)某市共有100万居民的月收入是通过“工资薪金所得”得到的，如图是抽样调查后得到的工资薪金所得X的频率分布直方图，工资薪金个人所得税税率表如表所示.表中“全月应纳税所得额”是指“工资薪金所得”减去3 500元所超出的部分(3 500元为个税起征点，不到3 500元不缴税).

工资个税的计算公式为“应纳税额”=“全月应纳税所得额”乘以“适用税率”减去“速算扣除数”.

全月应纳税所得额适用税率(%)速算扣除数不超过1500元30超过1500元至4500元10105超过4500元至9000元20555………

例如：某人某月“工资薪金所得”为5 500元，则“全月应纳税所得额”为5 500-3 500=2 000元，应纳税额为2 000×10%-105=95(元)

在直方图的工资薪金所得分组中，以各组的区间中点值代表该组的各个值，工资薪金所得落入该区间的频率作为x取该区间中点值的概率.

(Ⅰ)试估计该市居民每月在工资薪金个人所得税上缴纳的总税款；

(Ⅱ)设该市居民每月从工资薪金所得交完税后，剩余的为其月可支配额y(元)，试求该市居民月可支配额y的数学期望.

【命题构思意图】出题的时候，我们首先要构思两个有关联的随机变量X和Y，因此就想到了居民的月收入X和他的纳税额Y，二者之间的关系由税率表来呈现(这个关系其实是一个分段函数，而且这个分段函数模型在人教A版必修一教材中出现过，源于课本，对所有的同学来说背景是公平的)，居民的月收入X是用来作为已知条件给出的，呈现方式我们首选还是用频率分布直方图，那么，题目要出的问题就针对Y这个量来出，可以出Y的分布列、Y的期望等问题，但都觉得落入了俗套，所以最后我们还是出了求Y的总量这样的问题.

另外，用样本估计总体，用样本的频率分布估计总体的概率分布，这是统计这门课程的基本思想，因此，概率统计试题的命制不能离开这个主航道，所以我们在题目中以抽样调查后得到的工资薪金所得X的频率分布直方图来作为总体该市100万居民的月收入的概率分布，就是要体现统计这门课程的这一基本思想.

最后，如何用样本去估计总体？如何用样本的频率分布直方图去估计总体的概率分布？这是一个具体的操作技术层面的事情，在直方图中，往往以各组的区间中点值代表该组的各个值，以样本值落入该区间的频率作为总体取该区间中点值的概率，这是在频率分布直方图中经常采用的一种数据处理的手段，所以我们在题目中也希望能够制造机会，使考生展示这样的一种数据处理能力.

解：(Ⅰ)工资薪金所得的5组区间的中点值依次为3 000,5 000,7 000,9 000,11 000，x取这些值的概率依次为0.15,0.3,0.4,0.1,0.05，算得与其相对应的“全月应纳税所得额”依次为0,1 500,3 500,5 500,7 500(元)，按工资个税的计算公式，相应的工资个税分别为：

0(元)，

1 500×3%-0=45(元)，

3 500×10%-105=245(元)，

5 500×20%-555=545(元)，

7 500×20%-555=945(元)；

∴该市居民每月在工资薪金个人所得税上缴纳的总税款为

(45×0.3+245×0.4+545×0.1+945×0.05)×106=2.1325×108(元)；

(Ⅱ)这5组居民月可支配额y取的值分别是Y1,Y2,Y3,Y4,Y5，

Y1=3 000(元)；

Y2=5 000-45=4 955(元)；

Y3=7 000-245=6 755(元)；

Y4=9 000-545=8 455(元)；

Y5=11 000-945=10 055(元)；

∴Y的分布列为

Y300049556755845510055P0．150．30．40．10．05

∴该市居民月可支配额的数学期望为

E(Y)=3 000×0.15+4 955×0.3+6 755×0.4+8 455×0.1+10 055×0.05=5 986.75(元)

【解法指导】学生解这种含有两个随机变量的题型问题时，首先在审题时就要自觉的去捕捉题目里设置的是哪两个随机变量X和Y，其中X是已知的，它的呈现方式是哪种(呈现的方式有频率分布直方图、表格、茎叶图等)，Y是用来出题的，题目针对Y这个量出了一个什么样的问题，而Y与X的关系的呈现方式又是什么.要把这些题目中的要素迅速地提炼出来，然后进行数据处理.本题在具体进行数据处理时，在直方图中以各组的区间中点值代表该组的各个值、以样本值落入该区间的频率作为总体取该区间中点值的概率，这种手法是在频率分布直方图中经常采用的一种数据处理的手段，复习中希望考生牢固掌握在频率分布直方图中如何求中位数、均值、方差这些基本的数据处理能力.

【命题反思】本题第二问中又设计了一个量“该市居民月可支配额”，这样一来本题中就贯穿了三个量：月工资薪金所得→全月应纳税所得额→月可支配额，这样就显得环节多了一点，一般来说高考题中只设置两个相关联的随机变量，这两个随机变量X和Y以一种函数关系呈现出它们彼此间的联系，本题设置了三个随机变量，就显得略多了一点，有重复考查之嫌.

二、注重对重要的概率模型进行考查

数据处理能力常常需要在“会用模型”这样一个平台上去展示，我们中学学习的超几何分布、二项分布、正态分布都是最常用、最经典的概率模型，所以，无论是高考还是模考，都会对这些重要的概率模型着重进行考查.

【例2】(2017年乌鲁木齐市高三第一次诊断性测试理科第19题)某地十余万考生的成绩近似地服从正态分布，现从中随机地抽取了一批考生的成绩，将其分成6组：第一组[40,50)，第二组[50,60)，……，第六组[90,100]，作出频率分布直方图如图所示.

(Ⅰ)用每组区间的中点值代表该组的数据，估算这批考生的平均成绩和标准差(精确到个位)；

(Ⅱ)以这批考生成绩的平均值和标准差作为正态分布的均值和标准差，设成绩超过93分的为“优”，现在从总体中随机抽取50名考生，记其中“优”的人数为Z，试估算Z的期望．

附：

若X～N(μ,σ2)，

则P(μ-σlt;Xlt;μ+σ)=0.683，

P(μ-2σlt;Xlt;μ+2σ)=0.954,

P(μ-3σlt;Xlt;μ+3σ)=0.997.

【命题构思意图】我们想设置一个情景来考查我们中学学习的超几何分布、二项分布、正态分布这些重要的概率模型，但是我们还是不忘用样本的频率分布估计总体的概率分布这一根本思想，因此我们设置出抽取一批考生的成绩，作出频率分布直方图这个背景(这相当于抽取了一个样本)，再用这个样本去估计总体正态分布的两个重要参数(均值和标准差)，以此来确定出这个总体正态分布.而正态分布的考查只限于P(μ-σlt;Xlt;μ+σ)=0.683，P(μ-2σlt;Xlt;μ+2σ)=0.954，P(μ-3σlt;Xlt;μ+3σ)=0.997这三个概率值，因此，我们在出题的时候就要精准地瞄准这些临界值才行,这样就考查了正态分布这个概率模型，但是，我们还希望考查超几何分布、二项分布这些重要的概率模型，所以我们就出了“现在从总体中随机抽取50名考生，记其中‘优’的人数为Z”这一问题，这个问题既可以纳入超几何分布概率模型、又可以纳入二项分布这个概率模型，但是我们故意在题目出示的已知条件“某地十余万考生的成绩近似地服从正态分布”里，模糊了总数“十余万考生”，这样你要想用超几何分布概率模型来做，计算上就行不通，最后就被“逼”到二项分布这个概率模型上来了.

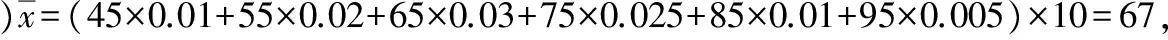
s2=(45-67)2×0.01×10+(55-67)2×0.02×10+(65-67)2×0.03×10+(75-67)2×0.025×10+(85-67)2×0.01×10+(95-67)2×0.005×10=166，

(Ⅱ)依题意X～N(67,13)，

P(μ-2σlt;xlt;μ+2σ)=P(41lt;xlt;93)=0.954，

∵Y～B(50,0.023)，∴E(Y)=50×0.023=1.15.

【解法指导】本题要求考生牢固掌握在频率分布直方图中如何求均值、方差这些基本的数据处理能力，能够对超几何分布、二项分布这些概率模型进行识别辨析和应用.

【命题反思】本题在“用样本的频率分布估计总体的概率分布”这样一个背景下设计考查了正态分布这个概率模型，但是，我们还希望考查超几何分布、二项分布这些重要的概率模型，所以我们就设置了“现在从总体中随机抽取50名考生，记其中‘优’的人数为Z”这一问题，这个问题既可以纳入超几何分布概率模型、又可以纳入二项分布这个概率模型，但是我们故意在题目出示的已知条件“某地十余万考生的成绩近似地服从正态分布”里，模糊了总数“十余万考生”，这样你要想用超几何分布概率模型来做，计算上就行不通，最后就被“逼”到二项分布这个概率模型上来了.总之，对超几何分布、二项分布这些概率模型的辨析和应用是非常重要的.

三、注重对重要的统计案例进行考查

数据处理能力还需要针对研究对象的特殊性，根据问题的具体情况，选择合适的统计方法整理数据，并构建模型对数据进行分析、推断,获得结论.我们中学学习的独立性假设检验、回归分析就是最常用、最经典的两个统计案例，所以，无论是高考还是模考，都会对这些重要的统计案例着重进行考查.

身高x(cm)60708090100110体重y(kg)6810141518＾e(1)0．410．011．21-0．190．41＾e(2)-0．360．070．121．69-0．34-1．12

(Ⅰ)求表中空格内的值；

(Ⅱ)根据残差比较模型①，②的拟合效果，决定选择哪个模型；

(Ⅲ)残差大于1 kg的样本点被认为是异常数据，应剔除，剔除后对(Ⅱ)所选择的模型重新建立回归方程.

(结果保留到小数点后两位)

【命题构思意图】我们中学学习的回归分析是最常用、最经典的一个统计案例，因此，我们想设置一个情景来考查这个统计案例，这首先需要构造两个“相关变量”，我们还是依据课本和学生都熟悉的生活经验，选择了身高与体重这两个量，再结合人教A版课本选修2-3上的残差分析的有关内容，我们首先要求考生对两个回归模型进行比较和评判，作出取舍和选择，最后剔除异常数据后再对所选择的那个模型重新建立回归方程.以达到优化回归方程的目的.在这样一个完整的过程中来考查考生对回归模型的理解掌握程度和数据处理能力.

(Ⅱ)模型①残差的绝对值的和为0.41+0.01+0.39+1.21+0.19+0.41=2.62，

模型②残差的绝对值的和为0.36+0.07+0.12+1.69+0.34+1.12=3.7，

2.62lt;3.7，所以模型①的拟合效果比较好，选择模型①.

(Ⅲ)残差大于1 kg的样本点被剔除后，剩余的数据如下表

身高x(cm)607080100110体重y(kg)68101518＾e(1)0．410．01-0．39-0．190．41

【解法指导】本题要求考生对建立回归模型、利用回归模型预测、评价回归模型、残差分析的方法等有关内容都有所了解，在这样一个完整的过程中来考查考生对回归模型的理解掌握程度和数据处理能力.虽然只是套公式做题，但是对计算能力的要求还是较高的，平时复习时养成把公式中的项目列成表再代入计算的习惯，按程序性知识的学习机制进行学习.

新疆兵团二中)