类比·探究·结论

安徽 李昭平

类比·探究·结论

安徽 李昭平

由一事物的性质类比联想到另一事物的相应性质，是近几年高考出现的一种新题型.这种问题，往往融直观想象、逻辑推理、数学运算等数学核心素养于一体，能有效考查学生的合情猜想、思维水平和综合能力.一般涉及到结构上、概念上、次数上、元数上、方法上的类比和探究，常见的有平面向空间类比、椭圆向双曲线类比、低次向高次类比、等差向等比类比、少元向多元类比等等.下面予以介绍，供参考.

1.平面向空间类比

【例1】我们知道：在平面几何中，△ABC的三条中线相交于一点，这个点叫三角形的重心,并且重心分中线之比为2∶1(从顶点到对边中点).据此，我们拓展到空间：把空间四面体的顶点与对面三角形的重心的连线叫空间四面体的中轴线，则四条中轴线相交于一点，这点叫此四面体的重心.类比上述命题，请写出四面体重心的类似性质,并证明.

【思路】将三角形边的中点类比到四面体面的重心,将三角形重心性质的证明方法类比到空间四面体中，利用相似三角形对应边成比例.

【解析】四面体重心的性质:空间四面体的重心分顶点与对面三角形的重心的连线之比为3：1(从顶点到对面三角形的重心).

事实上:如图,AE,BP为四面体的中轴线,P,E分别为△ACD,△BCD的重心,连接BE,AP并延长，交CD于点F,再连接PE.

因为AP∶PF=2∶1,BE∶EF=2∶1,

所以AP∶PF=BE∶EF,所以PE∥AB，

因此AG∶GE=BG∶GP=AB∶PE=3∶1.

【点评】一般地，平面上的“点、线、面”往往类比到空间上的“线、面、体”(元素类比)，比如平面上的三角形类比到空间上的四面体，平面上的角类比到空间的二面角，三角形的中位线类比到空间四面体的中位面，三角形的外接圆类比到三棱锥的外接球等等；平面上的数量结构形式往往类比到空间上的数量结构形式(结构类比)；平面上的“面积法”往往类比到空间上的“体积法”，平面上的“相似法”往往类比到空间上的“相似法”(方法类比).“将平面图形的性质类比到空间，探求相应的空间图形是否也有此类似的性质”，这是近几年高考考查立体几何出现的一种新题型.这种问题往往以平面图形的性质及其证法为基础，融探索、猜想、证明于一体，充分体现了新课改的理念.但要注意类比的结论不一定都正确，需要探究和证明.

VO-ABC+VO-BCD+VO-CDA+VO-DAB=VD-ABC(O为内切球的球心)

【答案】(Ⅰ)很容易证明，略去.

(Ⅱ)斜三棱柱各侧面面积与它所对棱所对应的二面角的正弦的比相等.

2.椭圆向双曲线类比

【思路】从椭圆问题的证法出发，结合双曲线的定义，类比前行.

这就是椭圆焦点三角形的一个面积计算公式.类比上述方法，推导双曲线焦点三角形的一个面积计算公式.

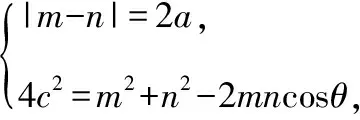
3.低次向高次类比

【思路】将字母a,b的次数升到3，仿上证明即可.

4.等差向等比类比

【思路】从等差数列、等比数列的内在联系，以及和式的结构式出发进行类比联想.

只证充分性(必要性易证，略去).

【训练6】设数列{an}的前n项和为Sn,不难得到数列{an}为等差数列的充分必要条件：对任何n∈N*,都有Sn=An2+Bn(A,B是常数).证明不难,略去.由此向等比数列类比，写出结论，并证明之.

【答案】结论：设数列a1,a2,…,an中的每一项都不为零，且前n项和为Sn,则数列{an}为公比非1的等比数列的充分必要条件：对任何n∈N*,都有Sn=kqn-k(k,q是非零的常数).

证明：只证充分性(必要性易证，略去).

当n≥2时，an=Sn-Sn-1=(kqn-k)-(kqn-1-k)=k(q-1)qn-1.

当n=1时,a1=S1=kq-k=k(q-1).

所以an=k(q-1)qn-1,n∈N*.

因此{an}是等比数列.

5.少元向多元类比

【思路】从已知不等式的结构特征进行类比联想，推广到三元以上.

事实上，当n=3时，由已知不等式知，

假设n=k(k≥3)时，不等式成立，即

则当n=k+1时，

【点评】这里是将不等式中的三个字母拓展到n个字母，得到新的不等式，从中体会到类比的魅力.从少元向多元类比往往能拓展思维、发现新知，提高猜想和推理能力.比如x=1表示数轴上一个点，类比到二维空间就是单位圆x2+y2=1，再类比到三维空间就是单位球x2+y2+z2=1，如此等等.

安徽省太湖中学)