聚焦新定义，提升学科素养

山东 王中华

聚焦新定义，提升学科素养

山东 王中华

随着新课标的深入实施，数学素养教育要求不断提高，以能力立意为目标，以增大思维容量为特色，具有相当浓度和明确导向的创新题型脱颖而出.“新定义”型题目是高考命题的一大热点.所谓“新定义”型问题，主要是指在问题中定义了中学数学中没有学过的一些新概念、新运算、新符号，要求学生读懂题意并结合已有的知识、能力进行理解，并根据新的定义进行运算、推理、迁移的一种题型.这类题目具有启发性、思考性、挑战性和隐蔽性等特点，由于它构思巧妙，题意新颖，是考查学生综合素质和能力、挖掘学生潜力的较佳题型，因而它受到命题者的青睐.这种类型的问题很多，一般是以新课标教材内容为背景，给出某种新概念、新运算(符号)、新法则(公式)等，学生在理解相关新概念、新运算(符号)、新法则(公式)之后，运用新课标学过的知识，结合已掌握的技能，通过推理、运算等寻求问题解决.纵观这几年的高考试题，可以发现，“新定义”型问题按其命题背景可分为三种类型：以新课标内容为背景、以高等数学为背景、以跨学科为背景.现就相关类型作探讨.

1.新定义集合

所谓“新定义集合”，给出集合元素满足的性质，探讨集合中的元素属性，要求有较高的抽象思维和逻辑推理能力.由于此类题目编制角度新颖，突出能力立意，突出学生数学素质的考查，特别能够考查学生“现场做题”的能力，并且在近几年高考模拟试题和高考真题中频繁出现.解题时应时刻牢记集合中元素的三要素：确定性，互异性，无序性

( )

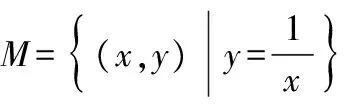
A.①③ B.②③ C.②④ D.③④

【答案】B

2.新定义函数

【例2】如果函数f(x)对任意两个不等实数x1,x2∈(a,b)，均有x1f(x1)+x2f(x2)gt;x1f(x2)+x2f(x1)，则称函数f(x)为区间(a,b)上的“G”函数，给出下列命题：

①函数f(x)=2x-sinx是R上的“G”函数;

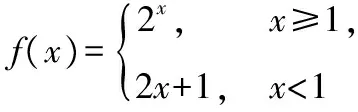
④若函数f(x)=ex-ax-2是R上的“G”函数，则a≤0.

其中正确命题的个数是

( )

A.1 B.2 C.3 D.4

【答案】C

【解析】本题看似所给不等式复杂，但稍作变形可得x1[f(x1)-f(x2)]+x2[f(x2)-f(x1)]gt;0，所以(x1-x2)[f(x1)-f(x2)]gt;0，即(x1-x2)与[f(x1)-f(x2)]同号，得到出新定义实质：f(x)是(a,b)上的增函数.可从单调性的角度判断四个命题，①：f′(x)=2-cosxgt;0恒成立，所以f(x)是R上的增函数；②③：可通过作出函数的图象来判断分段函数是否在给定区间上单调递增，通过作图可知②正确，③不正确；④：若f(x)是“G函数”，则f(x)是R上的增函数，所以f′(x)=ex-a≥0，即a≤ex恒成立，因为ex∈(0,+∞)，所以可得a≤0，④正确.

综上所述，①②④正确，共有三个正确命题，故选C.

点评：本题考查新定义问题、函数的单调性、学生对知识的综合运用能力及运算能力，属难题.

3.新定义数列

【例3】(2016·江苏)记U={1,2,…，100}.对数列{an}(n∈N*)和U的子集T，若T=∅,定义ST=0;若T={t1,t2,…，tk}，定义ST=at1+at2+…+atk.例如：T={1,3,66}时，ST=a1+a3+a66.现设{an}(n∈N*)是公比为3的等比数列，且当T={2,4}时，ST=30.

(Ⅰ)求数列{an}的通项公式；

(Ⅱ)对任意正整数k(1≤k≤100)，若T⊆{1,2,…，k}，求证：STlt;ak+1；

(Ⅲ)设C⊆U,D⊆U,SC≥SD,求证：SC+SC∩D≥2SD.

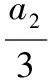
(Ⅲ)下面分三种情况证明.

①若D是C的子集，则SC+SC∩D=SC+SD≥SD+SD=2SD.

②若C是D的子集，则SC+SC∩D=SC+SC=2SC≥2SD.

③若D不是C的子集，且C不是D的子集.令E=C∩UD，F=D∩UC，则E≠∅，F≠∅，E∩F=∅.

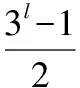
点评：本题三个难点，一是数列新定义，利用新定义确定等比数列首项，再代入等比数列通项公式求解，二是利用放缩法求证不等式，放缩目的是将非特殊数列转化为特殊数列，从而可利用特殊数列性质，以算代证，三是结论含义的应用，实质又是一个新定义，只不过是新定义的性质应用.

4. 定义新运算型

( )

A.[-1，2] B.(0，3]

C.[0，2] D.[1，3]

【答案】C

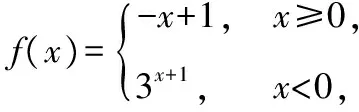
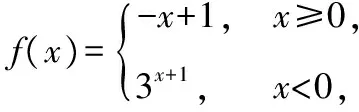
5.定义新法则型

思路分析：根据二元码及新定义，分析新定义的特点，按照所给的数学规则和要求进行逻辑推理和计算求得.

【答案】5

【解析】由题意得相同数字经过运算后为0，不同数字运算后为1.由x4⊕x5⊕x6⊕x7=0可判断后4个数字出错；由x2⊕x3⊕x6⊕x7=0可判断后2个数字没错，即出错的是第4个或第5个；由x1⊕x3⊕x5⊕x7=0可判断出错的是第5个，综上，第5位发生码元错误.

点评：本题以二元码为背景考查新定义问题，解决时候要耐心读题，并分析新定义的特点，按照所给的数学规则和要求进行逻辑推理和计算等，从而达到解决问题的目的.对于新法则，关键在于找到元素之间的对应关系，我们可以借助图表等方法寻找它们之间的对应关系，利用对应关系列方程.

6.以高等数学为背景

本类型的题目通常是以高等数学符号、概念直接出现或以高等数学概念、定理作为依托融于初等数学知识中.此类问题的设计虽来源于高等数学，但一般是起点高，落点低，它的解决方法还是运用中学数学的基本知识和基本技能.这要求学生认真阅读相关定义或方法，在充分理解题意的基础上，结合已有的知识进行解题.

( )

A.8 B.6 C.4 D.1

【答案】A

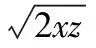
7.以跨学科为背景

本类型的题目，主要是介绍数学知识在其他学科或领域的运用，一般都会介绍运用时的知识背景、数学模型，因而题中文字、信息较多.学生必须准确地把握题意、理顺线索、分析相应数学模型与数学知识的内在联系，结合学生已有的知识和能力进行推理、运算.

【例7】(2016·北京理)设数列A：a1，a2,…aN(N≥1).如果对小于n(2≤n≤N)的每个正整数k都有aklt;an，则称n是数列A的一个“G时刻”.记G(A)是数列A的所有“G时刻”组成的集合.

(Ⅰ)对数列A：-2，2，-1，1，3，写出G(A)的所有元素；

(Ⅱ)证明：若数列A中存在an使得angt;a1，则G(A)≠∅；

(Ⅲ)证明：若数列A满足an-an-1≤1(n=2,3,…,N),则G(A)的元素个数不小于aN-a1.

思路分析：(Ⅰ)关键是理解G时刻的定义，根据定义即可写出G(A)的所有元素；(Ⅱ)要证G(A)≠∅，即证G(A)中含有一元素即可；(Ⅲ)当aN≤a1时，结论成立.只要证明当aNgt;a1时仍然成立即可.

【解析】(Ⅰ)G(A)的元素为2和5.

(Ⅱ)证明：因为存在an使得angt;a1，所以{i∈N*|2≤i≤N,aigt;a1}≠∅.

记m=min{i∈N*|2≤i≤N,aigt;a1}，则m≥2，且对任意正整数klt;m,ak≤a1lt;am.因此m∈G(A)，从而G(A)≠∅.

(Ⅲ)证明：当aN≤a1时，结论成立.以下设aNgt;a1.由(Ⅱ)知G(A)≠∅.

设G(A)={n1,n2,…,np}，n1lt;n2lt;…lt;np，记n0=1.

则an0lt;an1lt;an2lt;…lt;anp.对i=0,1,…,p，记Gi={k∈N*|nilt;k≤N,akgt;ani}.

如果Gi≠∅，取mi=minGi，则对任何1≤klt;mi,ak≤anilt;ami.

从而mi∈G(A)且mi=ni+1.又因为np是G(A)中的最大元素，所以Gp=∅.从而对任意np≤k≤n，ak≤anp，特别地，aN≤anp.

对i=0,1,…,p-1,ani+1-1≤ani.

因此ani+1=ani+1-1+(ani+1-ani+1-1)≤ani+1.

点评：数列的实际应用题要注意分析题意，将实际问题转化为常用的数列模型.数列的综合问题涉及到的数学思想：函数与方程思想(如：求最值或基本量)、转化与化归思想(如：求和或应用)、特殊与一般思想(如：求通项公式)、分类讨论思想(如：等比数列求和，q=1或q≠1)等.

山东省枣庄市第二中学)