似曾相见曾相识，看似平淡需真功——2017年全国卷解析几何试题赏析

安徽 朱启州

似曾相见曾相识，看似平淡需真功
——2017年全国卷解析几何试题赏析

安徽 朱启州

2017年全国卷解析几何命题，以运算求解能力为基础，思维能力为核心，问题设置侧重体现对知识的理解和应用，对考生逻辑思维的广度和深度、运算求解能力等有较高要求.整体上试题特点可用“似曾相见曾相识，看似平淡需真功”来概括.

一、合情推理总相宜

( )

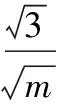
综上所述m∈(0,1]∪[9,+∞)，故选A.

【点拨】对于C上存在点M满足∠AMB=120°，若用设而不求法，进而转化为任意性、存在性问题来解决，就费时费力.特殊化、极端化等方法是解决选择题常用方法.对本题来说M位于短轴端点时，∠AMB最大；越近于长轴端点，∠AMB越小，于是有椭圆C上存在点M满足∠AMB=120°，只要∠AMB≥120°即可.这种解决问题的方法主要运用合情推理,在平时数学问题解决中，我们往往自动化式应用这种思维方式，而不是有意识地使用罢了.因此，合情推理是发现与探寻解决数学问题时首要的思考方式，具有普遍适用性.

二、看似容易需真功

面对选择题，一般我们先通过对比筛选，在其中的两个答案中选出正确答案而今年命题人不愿给我们这个机会，非要考考你的真本事.

【例2】(2017·全国卷Ⅰ理·10)已知F为抛物线C：y2=4x的焦点，过F作两条互相垂直的直线l1，l2，直线l1与C交于A，B两点，直线l2与C交于D，E两点，则|AB|+|DE|的最小值为

( )

A．16 B．14

C．12 D．10

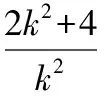
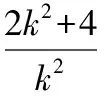
当且仅当k=±1时等号成立，|AB|+|CD|的最小值为16，故选A.

由解法一，知k2x2-2k2x-4x+k2=0,

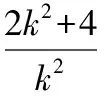
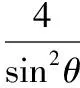
≥4×(2+2)=16.

作准线的垂线段AM，作x轴的垂线段AH，由抛物线的几何性质，

得|AF|=|AM|=|NH|=|NF|+|FH|=2+|AF|cosθ,

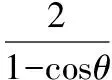
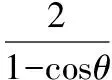
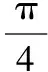
【评析】抛物线的焦半径、焦点弦问题，通常利用抛物线定义转化为点到准线的距离解决较方便；也可看作交点弦问题，通过直线方程与圆锥曲线方程联立，利用韦达定理求弦长，这也是通法.而最值问题通常要用函数方法或基本不等式来解决,都是通性通法.

三、缜思细算，显智慧

2017全国卷数学解析几何问题，看似起点不高，似曾相识，但完整解决问题并不容易.整体上看，与往年相比对学生运算求解能力、思维能力要求明显提高了.

(Ⅰ)求C的方程；

(Ⅱ)设直线l不经过P2点且与C相交于A，B两点.若直线P2A与直线P2B的斜率的和为-1，证明：l过定点.

(Ⅱ)分析发现问题应是直线与圆锥曲线关系问题，通常我们设l的方程，然后与曲线方程联立，再应用韦达定理解决.当涉及直线斜率时，要注意考虑斜率是否存在.于是我们分两种情况讨论.

当l的斜率存在时，设直线l的方程为y=kx+n(n≠1),A(x1,y1),B(x2,y2)，

得(1+4k2)x2+8knx+4n2-4=0,

又因为n≠1,所以n=-2k-1,Δ=-64kgt;0,

只要klt;0即可.

于是直线l的方程为y=kx-2k-1,

即y=k(x-2)-1,

所以直线l过定点(2,-1).

安徽省淮北市杜集区教育局教研室)