算不下去了怎么办？——从一道解析几何试题的解法说起

安徽 陈晓明

算不下去了怎么办？
——从一道解析几何试题的解法说起

安徽 陈晓明

这是笔者所在学校(省级示范高中)一道高三联考数学(文科)试题，考场上此题让大多数的同学或束手无策，或半途而废，得分率极低．许多同学都是在计算过程中遇到障碍，算到最后算不下去了.算不下去了怎么办?于是在试卷讲评课上笔者带领学生对该题解法一探究竟，以求找到困难原因，掌握此类问题解题策略．结果课堂上精彩纷呈，生成不断，带来好多意外收获！课后让我久久难忘，引起笔者对数学课堂教学的再次思考，一心想再次回味课堂，不断反思，不断提高……

为了保持课堂的原汁原味，还是先回到课堂．

1．课堂实录

首先在黑板上展示题目：

( )

接下来教师让学生充分思考，动笔去解，老师在学生中巡视……

教师：谁来谈谈你的看法？

这时班上有名的数学王子发话了．

学生1(解法1)：如图所示，

令切点为M，显然切线F1M的斜率不为0，

故可令切线F1M的方程为x=my-c，

即x-my+c=0．因为OM⊥F1C，

所以点O到切线F1M:x-my+c=0的距离

d=R=|OM|=a，

c2(b2-a2)y2-2acb3y+a2b4=0．②

(接下来本想通过十字相乘法解方程，可尝试几次未成功．只好用公式法解方程！)

因为Δ=4a4b4c2，

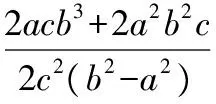
因为|CD|=|CF2|，所以由两点间距离公式得方程

这个方程太恐怖！

接下来算不下去了……

教师：你的解法很自然朴素，属通性通法．而且你很有魄力，敢于尝试！学习数学需要你这种勇敢精神！解出C点坐标，得到方程③很不容易．令人遗憾的是方程③确实复杂，算起来太麻烦，我们同学可以课后去挑战一下！许多同学也是到这里算不下去了，算不下去了怎么办？是硬着头皮慢慢算，还是另辟蹊径？在考场上要算出来肯定是得不偿失，因为需要时间太多了．

就在这时，数学课代表举手了．

学生2(解法2)：由双曲线定义得

|CF1|-|CF2|=2a，又|CD|=|CF2|，

故|CF1|-|CD|=2a．即|F1D|=2a．

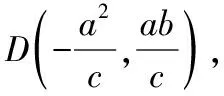
化简得b4+a2b2=4a2c2,

即(c2-a2)2+a2(c2-a2)=4a2c2,

进一步化简可得c2=5a2,

教师：厉害！简单多了．在圆锥曲线中定义法是解题的灵魂，真是不假．看来，当我们算不下去的时候，换个思路，可能峰回路转，柳暗花明！这里的关键是转化思想，利用双曲线定义及已知条件，巧妙地将用两次两点间距离公式(|CD|=|CF2|)转化为只用一次(|F1D|=2a)，从而成功回避了求C点坐标．

我刚讲到这儿，平时一直喜欢动脑的姚同学可能是看到别人得了表扬也想证明自己，他插了一句话．

学生3：D点坐标也不用求．

他这句话像平地惊雷，把大家都惊呆了，觉得不可思议！

教师：那你快说说看．

所以OD⊥F1M，

又由圆的切线的性质定理知OM⊥F1M，

故点D与点M重合．这样在Rt△OMF1中(如图所示)，

因为|F1M|=|F1D|=2a，

所以由勾股定理得4a2+a2=c2．

教师：太神奇了！算不下去了怎么办？退一步海阔天空．姚同学有一双敏锐的眼睛，竟然发现点D与点M重合，这样计算双曲线的离心率只需口算，计算量一下由地狱走到天堂，不战而胜，真是太爽了！

这时班上同学都发出惊叹的唏嘘声，向姚同学投去了钦佩的目光！

就在笔者准备鸣锣收兵时，平时有点内向的刘同学可能是被课堂气氛所感染，他举手了．

学生4(解法4)：求切线F1M的斜率可直接在Rt△OMF1中求(如图所示)：

因为|OM|=a，|OF1|=c，所以|F1M|=b．

教师：对呀．真聪明．这样求切线F1M的斜率的方法又简单了．

教师：解析几何题是高考中的必考题．经常有计算量较大的试题出现，对我们同学的计算能力是一个考验．特别是有时候因方法不当出现算不下去的局面，算不下去了怎么办？这时我们可能要多一些思路，不能在一棵树上吊死，否则考试时间不允许．对同一个问题，可从不同的视角来进行思考，可能会有新的发现：某些点是特殊点，某些值是特殊值，某些直线处于特殊位置，某些线有特殊的位置关系……这时就是踏破铁鞋无觅处，得来全不费工夫了！就算是没有简便方法，同样的算式我们也可能找到一些计算技巧，使计算简化．

此时下课铃声响起！

我看到了学生脸上的表情：惊叹之余，有些不舍和遗憾！

2．教学思考

看来，我们教师要充分相信学生，教学中要多给学生一点自由思考的时间，教师不能只按照自己事先想好的思路来教学，否则就会限制学生的思维，强扭学生的思维，题目刚出来就先进行提示或分析，那样做会扼杀学生的自主思维能力，剥夺学生的自由创造空间．在学生还没来得及思考的时候，老师硬是用自己固定的思路框定他们的头脑，使他们服从于已有的模式，这对他们思维能力的形成是个不小的打击．

离开了学生的“自主活动”“智力参与”“个人体验”就没有真正的学习了．把课堂还给学生，引发学生积极思维，让每位学生在数学思维的世界里自由地翱翔，向习题课教学要效益，通过问题解决，促进学生对数学知识的理解，让每位学生主动、积极地参与教学．当然，要做到这点，首先教师对习题的本身要有深入的研究，其次，对学生的课堂参与要给予足够的激励和引导．把课堂还给学生，注意倾听他们的声音，点燃他们的思维之火．

到这里，我想起叶澜教授曾说：“课堂是向未知方向挺进的旅程，随时都有可能发现意外的通道和美丽的因素，而不是一切都必须遵循固定路线而没有激情行程．”

3．结束语

安徽省宁国中学)