自主招生力学问题讲与练

江苏

吴 俊 苏忠明

自主招生力学问题讲与练

吴 俊 苏忠明

圆梦名校是每一个学子的追求，随着高校招生制度的改革，圆梦名校的途径变多，如自主招生考试，但是自主招生的考试紧跟高考之后，复习时间很短，没有统一的考纲、教材，给学生准备带来一定的困难。本刊经过了5年的探索和沉淀，坚持以高考内容为基础，适度提高，引用自主招生真题讲练，让学生在课余、假期适当地了解自主招生命题的内容、难度与动向。实践证明本刊取得了良好的效果，形成了独有的口碑栏目，所以今年应广大师生之需再次延续撰文。

一、物体的平衡问题

图1

(2)有固定转轴的物体的平衡条件：合力矩为零，∑M=0或∑M+=∑M-。

【例1】(2010·清华自招)如图2所示，用等长绝缘线分别悬挂两个质量、电量都相同的带电小球A和B，两线上端固定于O点，B球固定在O点正下方。当A球静止时，两悬线夹角为θ。能保持夹角θ不变的方法是

( )

图2

A.同时使两悬线长度减半

B.同时使A球的质量和电量都减半

C.同时使两球的质量和电量都减半

D.同时使两悬线长度和两球的电量都减半

图3

【答案】BD

【点评】(1)求解平衡问题方法。有正交分解法、矢量三角形定则法、拉密定理法等，这些高考复习中都会应用到，但是力矩平衡法高考不做要求(上海除外)。

二、牛顿运动定律及应用

(1)牛顿第二定律数学表达式为：∑F=ma，为矢量式。应用对象可以是单个物体，也可以是多个物体组成的系统。

(2)力的独立作用原理：物体同时受到几个外力时，每个力各自独立地产生一个加速度，就像别的力不存在一样，这个性质叫做力的独立作用原理。物体的实际加速度就是这几个分加速度的矢量和。

牛顿第二定律的分量形式：∑Fx=max，∑Fy=may。

(3)牛顿第二定律不仅对单个质点适用，也适用于质点组，对质点组运用牛顿第二定律的表达式为：F合=m1a1+m2a2+m3a3+…+mnan。当系统各物体相对静止时，a1=a2=a3=…=an，当加速度不同，就用通式F合=m1a1+m2a2+m3a3+…+mnan。

【例2】(2010·清华自招)在光滑的水平面上有一质量为M、倾角为θ的光滑斜面，其上有一质量为m的物块，如图4所示。物块在下滑的过程中对斜面压力的大小为

( )

图4

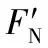
对m有FNsinθ=m(a1cosθ-a2)

mg-FNcosθ=ma1sinθ

图5

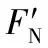
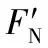
【答案】C

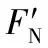
三、抛体运动

平抛运动高考必须掌握。斜抛运动的规律如下：

任一时刻的速度：vx=v0cosθ，vy=v0sinθ-gt。

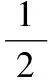
竖直上抛运动、平抛运动可分别认为是斜抛运动在θ=90°和θ=0°时的特例。

斜抛运动具有对称性，在同一段竖直位移上，向上和向下运动的时间相等；在同一高度上的两点处速度大小相等，方向与水平方向的夹角相等；向上、向下的运动轨迹对称。

【例3】(2014·卓越自招)如图6所示，滑雪运动员从初始(光滑)滑道上下降45 m后起跳，起跳角度与水平面的夹角为30°，且起跳不损失动能。降落滑道可看作倾角为30°的斜面，求运动员在空中飞行的时间及落地时速度与斜面的夹角。(g取10 m/s2)

图6

【解析】运动员从初始(光滑)滑道上下降45 m过程中，

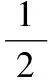
之后运动员做斜抛运动，运动员起跳后的运动分解为沿斜面(x)方向和垂直于斜面(y)方向的匀变速直线运动,如图7所示

图7

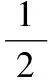
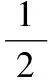
代入数据解得t=6 s

【拓展】抛物运动的共同特点是加速度相同，因此，当研究多个抛体的运动规律时，以自由落体为参照物，则各物体的运动均为匀速直线运动，这种选择参照物的方法，能大大简化各物体运动学量之间的联系，使许多看似复杂的问题简单、直观。

四、动能定理

对于单一物体(可视为质点)∑W=Ek2-Ek1，只有在同一惯性参照系中计算功和动能，动能定理才成立。当物体不能视为质点时，则不能应用动能定理。

对于几个物体组成的质点系，因内力可以做功，则∑W外+∑W内=∑Ek2-∑Ek1，同样只适用于同一惯性参照系。

在非惯性系中，质点动能定理除了考虑各力做的功外，还要考虑惯性力做的功，其总和对应于质点动能的改变。此时功和动能中的位移、速度均为相对于非惯性参照系的值。

【例4】(2013·北约自招)某车辆在平直路面上作行驶测试，测试过程中速度v(带有正负号)和时间t的关系如图8所示。已知该过程发动机和车内制动装置对车辆所作总功为零，车辆与路面间的摩擦因数μ为常量，试求μ值。数值计算时，重力加速度取g=10 m/s2。

图8

倒车过程根据动能定理有W2+Wf2-μmgx2=0

根据题意有W1+Wf1+W2+Wf2=0

由图象得x1=21 m，x2=6 m

【总结】使用动能定理解决多过程问题时，要注意几个运动性质不同的分过程中，有些力是全过程都起作用的，有些力在分过程中起作用，所以求解功时要分清，计算时要把各力的功连同符号(正负)一同代入公式。

五、功能关系

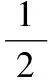
(3)机械能守恒：当质点系满足：W外+W非保内=0，则ΔE=0即Ek+Ep=Ek0+Ep0=常量。

(4)功能原理：物体系外力做的功与物体系内非保守力做的功之和，等于物体系机械能的增量。即∑W外+∑W非保守=∑E2-∑E1。

【例5】(2013·卓越自招)如图9所示，斜面固定在地面上，A与斜面无摩擦，B与绳无摩擦，mA=m，mB=2m，g已知，B离地面高度为h。

图9

(1)求绳上拉力；

(2)求A沿斜面上升的最大位移。

(2)对AB系统分析，AB开始运动到B刚好接触地面，满足机械能守恒定律，有：ΔE增=ΔE减

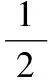
B落之后A继续上冲直到速度为0，根据机械能守恒定律或动能定理有

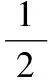
六、动量守恒定律与能量守恒定律的综合应用

【例6】(2011·华约自招)如图10所示，竖直墙面和水平地面均光滑，质量分别为mA=m，mB=3m的A、B两物体如图所示放置，其中A紧靠墙壁，AB之间有质量不计的弹簧相连。现对B物体缓慢施加一个向左的力，该力做功W，使AB之间弹簧被压缩但系统静止，后突然撤去向左推力解除压缩，求：

(1)从撤去外力到物体A运动，墙壁对A的冲量大小；

(2)AB都运动后，A、B两物体的最小速度各是多大？

图10

此时墙壁对A的冲量等于弹簧对A冲量的大小，也等于弹簧对B的冲量的大小，则

I=3mv-0

(2)弹簧恢复原长后，物体A的速度为最小值，为vAO=0，物体A离开墙壁后，弹簧伸长，A的速度逐渐变大，B的速度逐渐减小，当弹簧恢复原长时，物体A的速度达到最大值，为vA，物体B的速度减小到最小值，为vB，在此过程中系统的动量守恒，机械能守恒，有：

3mvBO=mvA+3mvB

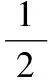
对于动量守恒定律，使用时要注意“四性”即矢量性、同时性、相对性、普适性。而追碰问题中要注意系统动量是否守恒、系统能量不能增加。

小试身手

( )

2.(2011·复旦大学)物体从具有共同底边、但倾角不同的若干光滑斜面顶端由静止开始自由滑下，当倾角为多少时，物体滑至底端所需的时间最短

( )

A.30度 B.45度

C.60度 D.75度

3.(2011·华约自招)如图所示，水流从与水平方向成α角的柱形管流入水平水槽，并有水槽左右两端流出，则从右端流出的水量与从左端流出的水量的比值可能为

( )

A.1+2sin2αB.1+2cos2α

C.1+2tan2αD.1+2cot2α

4.(2012·北约自招)两质量相同的卫星绕地球做匀速圆周运动，运动半径之比R1∶R2= 1∶2 ，则关于两卫星的下列说法正确的是

( )

A.向心加速度之比为a1∶a2= 1∶2

B.线速度之比为v1∶v2= 2∶1

C.动能之比为Ek1∶Ek2= 2∶1

D.运动周期之比为T1∶T2= 1∶2

5.(2016年北京大学科学营资格赛)将地面参考系处理为惯性系，蹲在水平地面上的少年猛地竖直向上跳起，过程中所受空气阻力可略。

(1)先写出惯性系中的质点系动能定理。再回答：少年跳起的过程中，哪些力是做正功，或者做负功？

(2)先写出惯性系中的质点系质心动能定理。再回答，少年起跳的过程中，哪些力是做正功，或者做负功？

6.(2013·北约自招)如图所示，将斜面分成三等分，从下到上依次为A、B、C和D，从A释放初速度为v0的小物体。若斜面光滑，小物体刚好到达D点，如果AB间有摩擦时，那么同样初速v0释放，小物体刚好到达C点然后滑下。求再次到达B以及A点时的速度vB和vA。

7.(2014·北约自招)如图所示，一个质量为2m的球和一个质量为m的球，用长度为2R的轻杆连在一起，两个球都被限制在半径为R的光滑圆形竖直轨道上，轨道固定于地面。初始时刻，轻杆竖直，且质量为2m的球在上方；此时，受扰动两球开始运动。求：

(1)当质量为2m的球运动到轨道最低点时，速度为多少；

(2)在(1)问的情况下，求轨道对两球组成的系统的力。

8.(2014·华约自招)在磁场中，一静核衰变成为a、b两核，开始分别做圆周运动。已知a和b两核圆周运动的半径和周期之比分别为Ra∶Rb=45∶1,Ta∶Tb=90∶117。此裂变反应质量亏损为Δm。求：

(1)a和b两核的电荷数之比qa/qb；

(2)a和b两核的质量数之比ma/mb；

(3)静核的质量数和电荷数；

(4)a核的动能Eka。

9.(2016·中科大自招)劲度系数为k=1 N/m的轻弹簧连接着两个质量均为m=2 kg的小球，静止于光滑水平桌面上。另一质量为M=10 kg的小球1，以速度v0撞向小球2，v0的方向沿着两小球2和3的连线方向，设碰撞为弹性的且碰撞时间极短。

(1)试问第一次碰撞刚结束时三个小球的速度分别是多少？

(2)第一次碰撞后，小球1、2有可能再次发生碰撞，试求第一次碰撞与可能的第二次碰撞之间小球1、2的位置随时间变化的关系；

(3)试由前面的结论判断小球1、2是否会发生第二次碰撞？如果发生，试估算前两次碰撞之间的时间间隔约为多少？如果不会发生，解释原因。

参考答案

5.(1)W内+W外=ΔEk(内力做功之和加上外力做功之和等于质点系动能增量)。过程中内力做功之和为正功，外力即重力做功之和为负功。

(2)W合外-C=ΔEkC(合外力对质心做功等于质心动能增量)。过程中地面竖直向上支持其做正功，重力做负功。

7.解：(1)根据机械能守恒有：

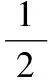
9.解：(1)对小球1、2组成的系统，根据动量守恒定律和机械能守恒定律，有

Mv0=Mv1+mv2①

联立①②式，得

化简，得-t=5sint

江苏省江阴市第一中学)