“滑块—滑板类”模型的解题策略

福建

邱基斌

“滑块 — 滑板类”问题微探。

“滑块—滑板类”模型的解题策略

邱基斌

一、“滑块—滑板类”模型的解题策略

1.考点分析

“滑块—滑板类”模型即滑块叠放在长木板上，当其中之一以某一初速度滑上另一物体(或在外力F的作用下)通过摩擦力带动另一物体运动的模型。“滑块—滑板类”模型题是力学中比较常见的问题，也是综合性很大的难题。其运动过程变化多端，运动状态隐蔽性较强，常常成为高考命题的重点和热点，在各地高考试题中频频出现。

2.解题思路

(1)审题建模：求解时应先仔细审题，清楚题目的含义、分析清楚每一个物体的受力情况、运动情况。

(2)求加速度：准确求出各物体在各运动过程的加速度(注意两过程的连接处加速度可能突变)。

(3)明确关系：找出物体之间的位移(路程)关系或速度关系是解题的突破口。求解中更应注意联系两个过程的纽带，每一个过程的末速度是下一个过程的初速度。

注意：

①“滑块—滑板类”模型关键是根据相对运动情况分析摩擦力的大小和方向，进而分析物块的运动性质和过程。尤其注意两者速度相同时刻，往往是摩擦力性质、大小及方向变化的临界点。

②两种位移关系：滑块由滑板的一端运动到另一端的过程中，若滑块和滑板同向运动，位移之差等于板长；反向运动时，位移之和等于板长。

3.临界条件

(1)滑块与滑板存在相对滑动的临界条件

①运动学条件：若两物体速度和加速度不等，则会相对滑动。

②动力学条件：假设两物体间无相对滑动，先用整体法算出一起运动的加速度，再用隔离法算出其中一个物体“所需要”的摩擦力Ff；比较Ff与最大静摩擦力Ffm的关系，若Ff>Ffm，则发生相对滑动。

(2)滑块滑离滑板的临界条件

当滑板的长度一定时，滑块可能从滑板滑下，恰好滑到滑板的边缘达到共同速度是滑块滑离滑板的临界条件。

4.常见的解法

“滑块—滑板类”模型问题往往存在一题多解情况，常见的解法如下：

(1)动力学分析法：分别对物块和滑板受力分析，根据牛顿第二定律求出各自加速度，然后结合运动学公式求解。

图1

二、典题精析

【例1】如图2所示，在光滑水平面上有一质量为m1的足够长的木板，其上叠放一质量为m2的木块。假定木块和木板之间的最大静摩擦力和滑动摩擦力相等。现给木块施加一随时间t增大的水平力F=kt(k是常数)，木板和木块加速度的大小分别为a1和a2，图3中反映a1和a2变化的图线正确的是

( )

图2

图3

【答案】A

【说明】解决此题的关键是分析出木块和木板“发生相对滑动”这一临界转折点，即当m1和m2之间的静摩擦力达到最大静摩擦力时，木块和木板将发生相对滑动。

【例2】如图4甲所示，静止在光滑水平面上的长木板B(长木板足够长)的左端放着小物块A。某时刻，A受到水平向右的外力F作用，F随时间t的变化规律如图4乙所示，即F=kt，其中k为已知常数。若物体之间的滑动摩擦力的大小等于最大静摩擦力Ff，且A、B的质量相等，则图5中可以定性地描述长木板B运动的v-t图象的是

( )

图4

图5

【解析】当F较小时，A、B整体具有共同的加速度，二者相对静止，当F较大时，二者加速度不同，将会发生相对运动，此后A做变加速直线运动，B做匀加速直线运动，为了求出两物体开始分离的时刻，必须知道分离时F的大小，此时采用整体法和隔离法分别列牛顿第二定律的方程即可。

选AB整体为研究对象，AB整体具有共同的最大加速度

【答案】B

【说明】当两者相对运动后，B将受恒力作用，做匀加速运动，可排除C、D选项，A、B选项的差别在于恰好相对运动的时刻，就需采用隔离法和整体法分别列方程了，也可以采用反证法，确定当F=Ff时是否相对滑动。所以，要注意总结解题方法。

【例3】质量M=9 kg、长L=1 m的木板在动摩擦因数μ1=0.1的水平地面上向右滑行，当速度v0=2 m/s时，在木板的右端轻放一质量m=1 kg的小物块如图6所示。当小物块刚好滑到木板左端时，物块和木板达到共同速度。取g=10 m/s2。求：

图6

(1)从木块放到木板上到它们达到相同速度所用的时间t；

(2)小物块与木板间的动摩擦因数μ2。

解法一:动力学分析法

(1)设木板在时间t内的位移为x1；木块的加速度大小为a1，木板的加速度大小为a2，时间t内的位移为x2，则有

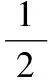
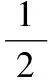
x1=L+x2③

v0-a1t=a2t④

联立①②③④代入数据得t=1 s。 ⑤

(2)根据牛顿第二定律，有

μ1(M+m)g+μ2mg=Ma1⑥

μ2mg=ma2⑦

联立④⑥⑦代入数据解得μ2=0.08。 ⑧

解法二:图象描述法

图7

(2)根据牛顿第二定律和图象意义有：

联立①②③代入数据解得v共=0.8 m/s，μ2=0.08。

【答案】(1)从木块放到木板上到它们达到相同速度所用的时间t为1秒 (2)小物块与木板间的动摩擦因数为0.08

【说明】本题关键是先根据运动学公式列式后联立求解出时间，然后再受力分析后根据牛顿第二定律列式求解；对于第(1)问，可以以长木板为参考系列式求解，会使问题大大简化。

【例4】如图8所示，质量M=0.4 kg、长为L=10 m的木板静止在光滑水平面上，一个质量m=0.1 kg的子弹以某一速度从右端射入木板。已知子弹可看做质点，子弹在木板中受到恒定的阻力f=0.8 N。若要使木板获得的速度不大于2 m/s，则子弹的初速度v0应满足的条件是

( )

图8

A.v0≤8 m/s

B.v0≤10 m/s

C.v0≥15 m/s

D.v0≥20 m/s

解法一:动力学分析法

(1)子弹未射出木板时两者已共速，由v0-a1t=a2t得v0=10 m/s，所以子弹的初速度v0≤10 m/s，选项B正确；

解法二:图象描述法

(1)子弹未射出木板，作出子弹、木板的v-t图象如图9甲所示。

图9

由题意知v0-8×1=2，解得v0=10 m/s，所以子弹的初速度v0≤10 m/s，选项B正确。

【答案】BC

福建省沙县第一中学)