基于DEA模型的中小学校园设施安全风险评估研究

高山，凌双



基于DEA模型的中小学校园设施安全风险评估研究

高山，凌双

(中南大学公共管理学院，湖南长沙，410083)

选取2013年中国30个省份(除西藏、台湾及港澳地区外)的中小学校园设施安全的省际数据为样本，综合运用两阶段Bootstrap-DEA模型和聚类分析方法，测算我国校园设施安全风险水平。结果表明：我国中小学校园设施安全风险总体上呈现出“东北地区＞东部地区＞中部地区＞西部地区”的趋势，且各地区之间风险水平呈现明显的差异性。准确衡量各地区中小学校园设施安全风险，有利于推动中小学校园设施安全从“粗放型”预防向“精准性”预防转变，以便制定出符合各地区实际情况的短期及中长期的校园设施安全管理政策。

中小学；校园设施安全；风险评估；Bootstrap-DEA模型；聚类分析

一、研究背景与文献综述

学校设施安全是指学校中的设施设备没有受到损坏从而不会导致人员伤害与财产损害，或者将人员伤亡与经济损失控制在可接受的水平状态下[1]。校园设施的安全与否不仅关系到学生的人身和财产安全，也关系到整个校园的安全和谐。但就目前来看，由校园设施问题引起的校园安全事故呈现出“事故频发，诱因复杂，影响严重”的特点。如2014年昆明“9·26”明通小学踩踏事故[2]、2016年北京市平谷区第六小学的“毒跑道”事件[3]等均对学校师生身心安全、校园公共财产产生了负面影响，严重影响了校园的稳定状态。在这种背景下，预防校园设施安全事故应前移事故预防关口，应将校园设施安全管理从“事后灭火”的应急管理转变为“事前预防”的风险管理。基于此，做好中小学校园设施安全风险评估工作，将有助于提升中小学校园设施风险识别能力，从源头预防突发 事件。

校园设施安全风险评估主要测算校园潜在的设施安全风险发生的概率以及由此造成的负面影响的程度。综合国内外文献，已有研究成果主要集中于校园安全的评估机制[4]、评估流程、评估主体、评估标准[5]以及评估制度[6]等定性研究上。而专门针对校园设施安全风险评估的定量研究主要有对校园建筑安全状况进行评价的，只是分析指标的权重高度依赖专家的经验、知识等，具有很强的主观性[7]。王起全运用非参数投影寻踪回归模型对中小学校园拥挤踩踏事故风险进行评价，指出人群失控、人群密度以及时间控制是影响校园踩踏事故的重要因素[8]。彭英等对校园体育设施安全事故开放案例进行事故树分析，识别出开放过程中的人、物、制度和环境4大类安全风险因素，但未对校园体育设施安全风险进行评估[9]。由此可见，国内外针对校园设施安全风险评估方面的研究和应用比较匮乏。

因此，本文引入数据包络分析方法(DEA,Data Envelopment Analysis)去评估中小学校园设施安全风险。针对经典DEA模型尚未考虑样本噪音对风险评估的干扰，本文运用中小学校园设施安全风险评估的两阶段Bootstrap-DEA模型，并选取2013年中国30个省份(除西藏、台湾及港澳地区外)的中小学校园设施安全的省际数据为样本，测算我国校园设施安全风险水平，以期为进一步降低校园设施安全风险提供指导信息。

二、研究设计

(一) 研究方法

数据包络分析(DEA)首次由Charnes引入并用于评估多指标投入与产出的不同决策单元的相对效 率[10]。其作为一种风险评估方法，无需事先确定风险评估表达式的形式以及权重信息，直接依赖于输入输出信息测算各决策单元的最优权重值，具有很强的客观性，主要集中于自然灾害[11]、道路安全[12]以及金融[13]等领域，几乎没有应用于校园安全领域风险的测算。其原理是将每个地区校园设施安全事故的发生看作一个“输入-输出”系统，通过数学规划测算决策单元的风险值离相对有效前沿面的距离，即离相对有效前沿面越远，风险越低，反之越高。因此，校园设施安全风险可以被定义为将校园设施安全风险信息等作为输入输出条件后校园安全事故的“爆发效率”，即校园设施安全风险值越大，则校园设施安全事故发生的可能性越高。其中“输入”是与校园设施安全相关的人员、资金、设施等，“输出”的是事故伤亡人数以及经济损失等。根据风险评估的流程，首先，确定风险评价目标为降低中小学校园设施安全事故发生率；其次，识别出校园设施安全的内外风险源，如个体风险、设施风险以及管理风险等；再次，对影响校园设施安全的各类风险源进行风险分析，同时综合内外风险分析提取出风险指标并进行相应的数据处理；复次，选择合适的模型，将处理好的数据输入对应的模型进行求解；最后，综合评判我国30个省份校园设施安全风险现状。所采用的风险评估流程如图1所示。

(二) DEA模型

DEA方法作为一种非参数评价方法，已经引起了国内外学者们的广泛关注。学术界先后提出了多阶段DEA模型和Bootstrap-DEA模型。Li M针对传统DEA模型无法区分处在有效前沿面上决策单元的相对风险，以及外生环境变量对灾害风险评估的影响，提出三阶段的Super-DEA模型[13]。为克服样本数据扰动问题，Simar和Wilson提出了一种Bootstrap的随机DEA方法，成功地解决了传统DEA模型样本选择问题[14]。上述两种方法均拓展了DEA模型，其中Li M聚焦于“过滤”掉外生环境变量对校园安全风险测算的影响，Simar和Wilson侧重于“剔除”随机冲击对风险评估造成的偏差。考虑到噪音数据对风险评估的干扰，本文参照Simar和Wilson提出的Bootstrap-DEA模型来评估我国30个省份的中小学校园安全风险。具体步骤如下所示。

1. 第一阶段：经典DEA模型

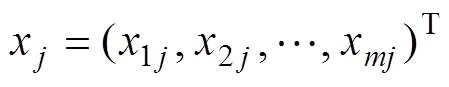
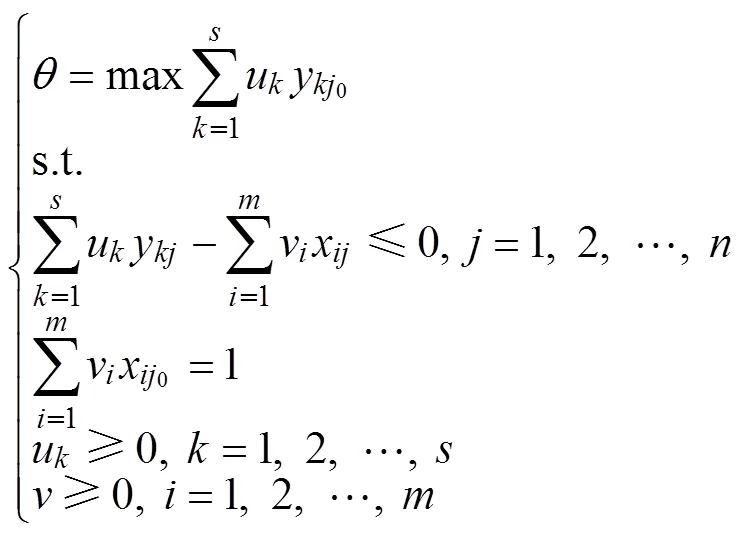
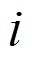
在经典DEA模型中，在0~1的范围内。若评价单元的值越接近1，说明投入产出水平越高，即评价单元的安全风险越高。尽管应用经典DEA模型在进行安全风险测算时，具有无需事先设定决策单元的风险评估表达式的优点，但由于未考虑到样本扰动等问题(如统计误差、样本太大以及遗漏变量等)，往往致使风险评估值偏高。因此，为克服上述不足，有必要进一步探讨样本随机因素对校园设施安全风险测算的影响。

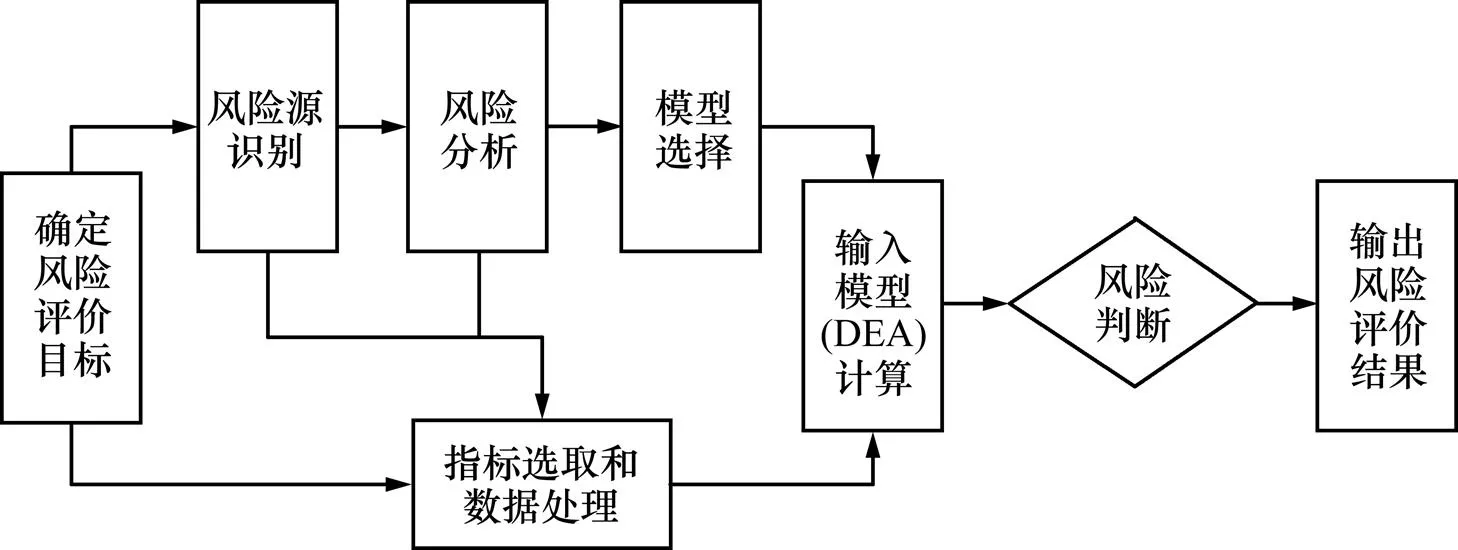
图1 校园设施安全风险评估流程图

2. 第二阶段：Bootstrap-DEA模型

鉴于经典DEA模型无法剔除外部随机性对风险评估结果的影响，本文在第二阶段运用Bootstrap方法，尽可能减少样本随机性对评估结果造成的偏差。其基本思想是对原始样本数据进行数值模拟，从而得到原始估计量的近似样本分布，进一步对总体的特征进行统计推断，具体步骤如下：

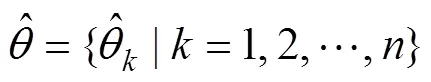
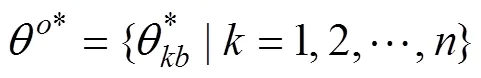
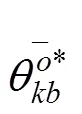
(e) 重复上述步骤B次(一般而言取B=200)，计算出每个决策单元初始风险得分的偏误，偏误修正值和估计区间，具体为：

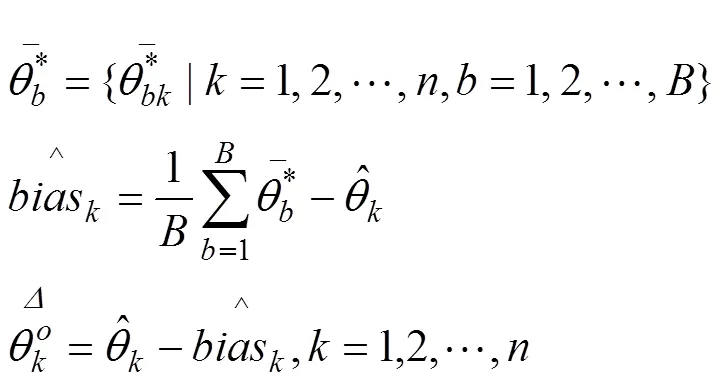
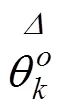
(三) 指标体系

运用DEA模型对校园设施安全风险进行评估的难点在于如何确定“风险投入”变量和“风险产出”变量。本文参考GB/T 13861(2009)及事故致因连锁理论[15]，并结合校园设施安全的定义及特点[1]，将校园设施安全风险因素划分为个体风险、设施风险及管理风险等风险源。相关研究表明：社会治安状况、安全意识水平、安全管理人员数量、与校园安全相关的财政投入、基础设施安全系数、安全教育频率、安全监督力度、师生安全防护及自救自护能力等均是影响校园设施安全的重要因素[16−18]。鉴于上述许多指标(如安全意识水平、自救自护能力等)的量化相对困难，本文选择学生密度、危房面积以及公共财政投入作为“风险投入”指标(见图2)。其中学生密度作为个体风险的替代指标，即学生密度越大，往往引发校园设施安全事故的可能性越大；危房面积作为设施风险的替代指标，即校园危房面积越大，师生受伤害的可能性越大。公共财政投入也是一项重要的“风险投入”指标，其主要通过对管理人员、设施质量等施加影响来提高校园设施安全水平，即公共财政对校园安全投入越大，校园设施安全水平越高。另外，由于校园设施安全事故并不像重大生产安全事故、道路交通事故以及自然灾害事故一样具有普遍性，大部分校园设施安全事故中经济损失这一项“风险产出”往往无法有效获取，因此需要寻找其他替代变量。一项比较合适的指标就是校园设施安全事故发生率。如果一个地区的校园设施安全风险相对较高，那么可以认为该地区的事前预防措施不到位。因此，校园设施安全事故率越高的地区，校园设施安全风险往往就越高。

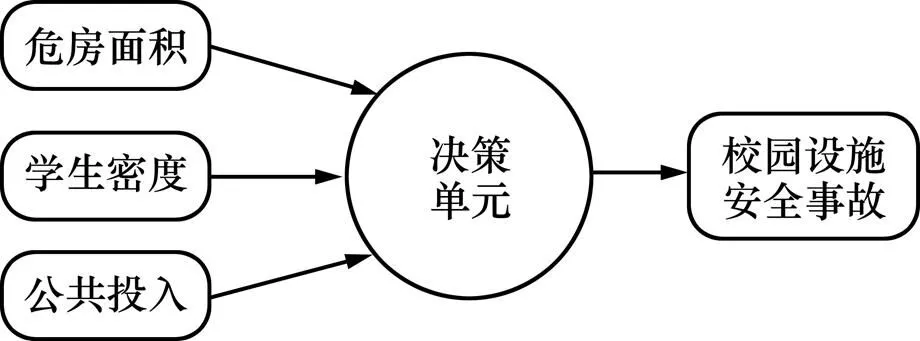
图2 DEA模型输入输出变量示意图

上述DEA模型所需的“风险投入”指标，如学生密度、危房面积、公共投入等数据主要来自于2013年《中国教育统计年鉴》《中国教育经费统计年鉴》以及相关统计年鉴等‚。由于当前我国暂无专业的校园安全事故的动态数据库，现实中往往也存在学校等责任方封锁事故消息，从而导致的事故统计不准确现象，因此，“风险产出”中的校园设施安全事故率等指标主要采用新闻合成周抽样法统计获取[19]。其基本思路为：在一年52个周(按一周七天计算)中，从第1-6周中随机抽取一个周一作为构造周的周一，从第47-52周中随机抽取一个周日作为构造周的周日，然后从第7-14周随机抽一个周二作为构造周的周二，依此类推，分别构造出周三、周四、周五、周六，形成一个完整的构造周。反复两次，得到一年的两个构造周样本。剔除通过上述方式获取的有遗漏、不全、异常的数据样本，最后得到了2013年30个省份中小学校园设施安全事故的样本信息。“风险投入”和“风险产出”变量的描述性统计信息如表1所示。另外，鉴于DEA模型的输入输出变量应满足正相关性，即“风险投入”值越大，“风险产出”值也越大，而公共财政投入为负指标，即值越大，校园设施安全风险越小，将公共财政投入指标采用取倒数方式进行逆处理[20]。

三、实证结果

(一) Bootstrap-DEA模型结果及分析

考虑到样本的随机性因素，根据表1中收集的“风险投入”与“风险产出”的数据，采用两阶段Bootstrap-DEA模型测算2013年我国30个省份中小学校园设施安全风险值。其中学生密度、人均危房面积以及公共投入等为“风险投入”变量、校园安全事故率为“风险产出”变量。具体结果如表2所示。

运用Bootstrap-DEA模型测算我国2013年30个省份中小学校园安全的风险值。结果显示：首先，我国中小学校园安全平均风险值为0.81，这说明了我国中小学校园安全风险整体相对较高，这也是我国中小学校园安全事故频发的重要原因。其次，采用Bootstrap方法进行风险测算值修正后，我国2013年30个省份中小学的校园安全风险水平均有不同程度的降低，较经典DEA模型测算的校园安全风险值下降了7.2%左右。且修正后的风险值均落在置信区间范围内(其中=0.05)，这意味着采用Bootstrap-DEA模型测算的各省中小学校园安全风险值落在上下界区间中具有95%的可信度。而经典DEA模型测算的风险值绝大部分落在边界之外，进一步论证了经典DEA模型的风险测算是有偏估计。再次，就校园安全风险值水平而言，江西、陕西两省中小学的校园安全风险最低，其相对风险值均低于0.6；而辽宁、山东、吉林等7省的中小学具有最高的校园安全风险，其相对风险值均高于0.9。通过数据分析可以发现，辽宁、山东、吉林3个省份均是财政基础建设投入过少且危房面积太多的区域，其中吉林省用于基础建设费用只有全国平均基础建设费用的15%左右，而危房面积却是全国平均危房面积的3倍。大部分省份中小学校园安全的相对风险值在0.6~0.9之间，其中风险值位于0.8~0.9之间的主要包括广东、浙江、上海、江苏等14个地区，位于0.7~0.8之间的主要包含广西、四川、湖南3个地区，剩余4个地区的中小学校园安全风险值处于0.5~0.7之间。最后，由于Bootstrap-DEA模型的测算风险修正值的变异系数为0.18，这说明全国30个省份的中小学校园安全风险呈现出明显的差异性。因此，为更清晰地描绘出全国30个省份中小学阶段校园安全风险的空间分布情况，同时考虑不同地区中小学校园安全风险的差异性，将各地区中小学校园的安全风险地图描绘如图3所示。

表1 校园设施安全“风险投入”与“风险产出”变量的描述性统计量

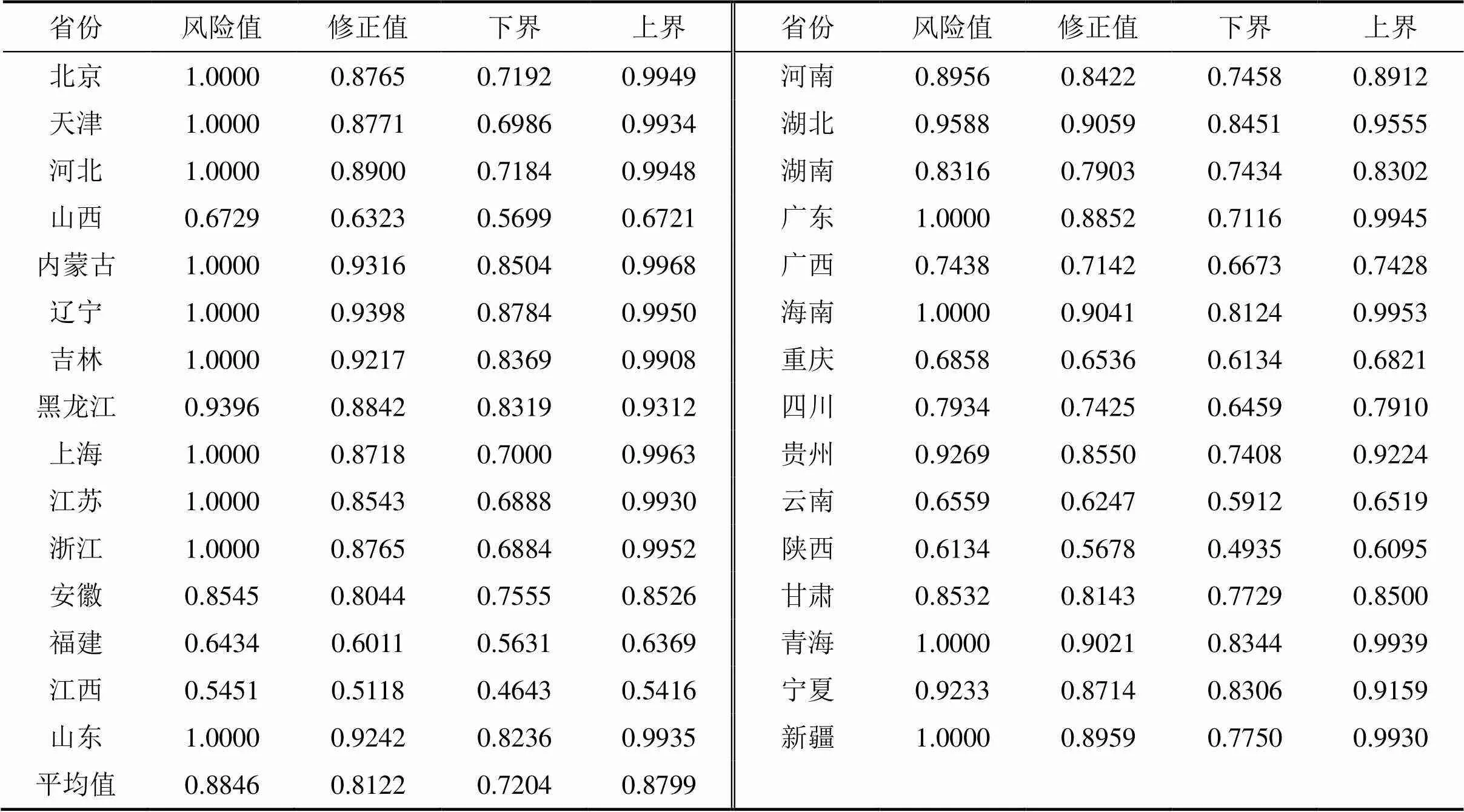
表2 我国2013年30个省份中小学校园设施安全风险测算值

从图3可以看出，我国中小学校园设施安全风险集中于我国东北部、东部地区，而中、西部等地区的中小学校园安全风险水平相对较低。且在地域上，我国中小学校园安全风险呈现出“东北地区＞东部地区＞中部地区＞西部地区”的趋势。其原因可能是我国绝大部分的人口分布在我国的东部地区，中西部地区的人口稀少；另外东北等地区的经济相对落后，致使校园安全基础设施投入不足且校园危房面积相对较大，进一步提高了该地区中小学校园设施安全的风险水平。

(二) 分类DEA模型结果及分析

鉴于不同地区校园设施安全内外部风险影响因子的不同，使得各地区中小学校园设施安全风险呈现出较大的差异性，为增强各地区(决策单元)中小学校园设施安全风险的可比性，本文采用聚类法对各地区进行分组，以便各地区教育部门可以与相同组别中风险最低的地区进行比较，有效识别两者之间的差别，从而提高其中小学校园设施安全风险的预防能力。通过采用R-2.25软件，按照其中中小学校园设施安全风险以及安全事故伤亡人数的不同对各地区进行聚类分析，共划分为4类，具体结果如表3所示。

通过表3可以看出，风险最高的地区位于群集4中，即东北地区。究其原因，东北地区的经济相对落后，对校园基础设施投入不足，可能导致校园设施无法正常更换和定期维护等，从而导致校园设施安全事故发生的可能性。而集群1包括我国的江西省、福建省、山西省、云南省以及重庆市5个省市，处于风险的最低层次。除去公共财政投入大等因素外，还与该类地区的学生密度相对较小、校园基础设施维护较好等因素有关。因此，为进一步评估2013年我国30个省份中小学校园安全风险，分别采用Bootstrap-DEA模型对4个集群内地区的中小学进行校园安全风险评估，以便为各组别中教育部门降低校园安全风险提供参照标杆。具体结果如表4所示。

总而言之，运用Bootstrap-DEA模型对各类别地区的中小学校园安全风险进行评估，各地区的风险相对值整体上保持递增顺序排列且最大风险值小于“1”。其中第3列表示群集1中的地区风险评估的结果，第4列表示群集1、2中的地区风险评估结果，依次类推。根据表4可以看出，由于同一类别中各省份的中小学校园设施安全风险处于相同水平，因此可以首先找到同类别中校园设施安全风险水平最低的地区作为标杆，通过比较两者的异同，以便初步提高校园安全风险管理能力，达到组内的风险最低。就类别间的比较而言，以群集1、2(组1-2)为例，首先在群集2中，中小学校园设施风险最高的地区为广西壮族自治区，风险最低的地区为湖南省，如果要将广西壮族自治区中小学校园安全风险降低至湖南省水平，需要减少2%左右的“风险投入”；然后，假使群集2中中小学校园安全风险水平最高的广西壮族自治区想要达到群集1中校园安全风险水平最低的江西省，那么广西壮族自治区需要在先前的基础上再减少15%左右的“风险投入”。综上所述，采用上述分类DEA模型有利于增强各决策单元间的可比性，便于各地区制定降低中小学校园设施安全风险的短期、中期以及长期目标。

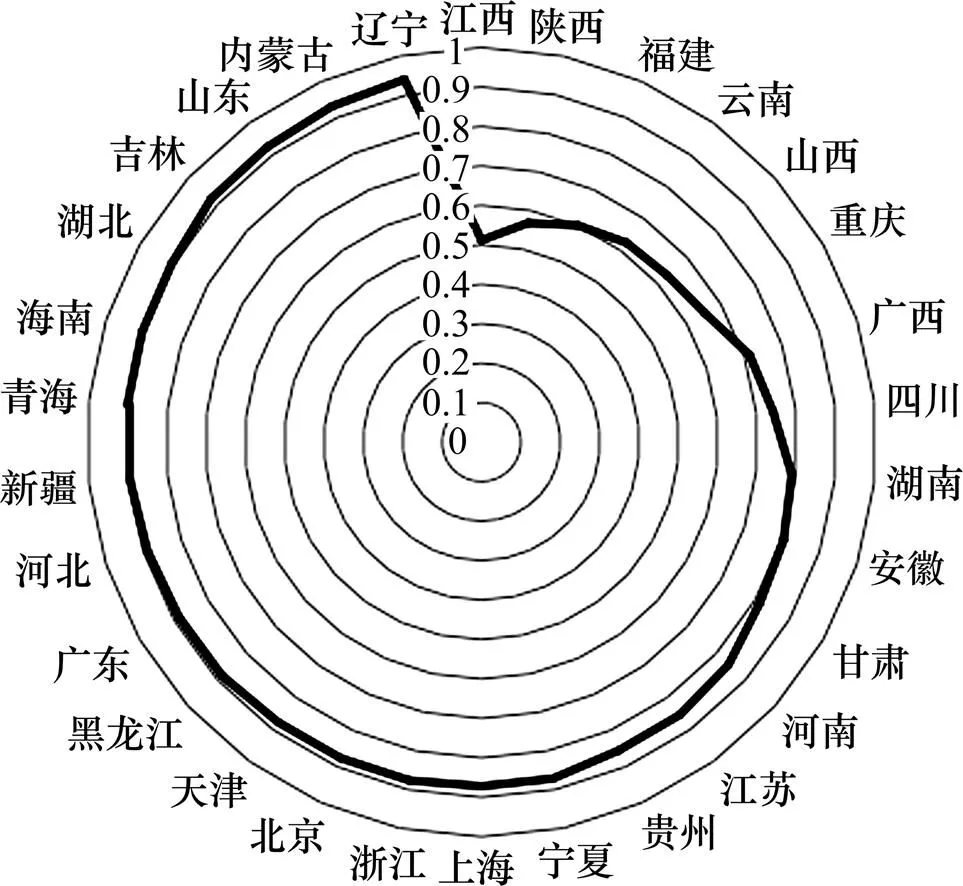
图3 全国30个省份校园安全风险地图

(除西藏、台湾及港澳地区外)

表3 我国30个省份(除西藏、台湾及港澳地区)中小学校园设施安全风险聚类结果

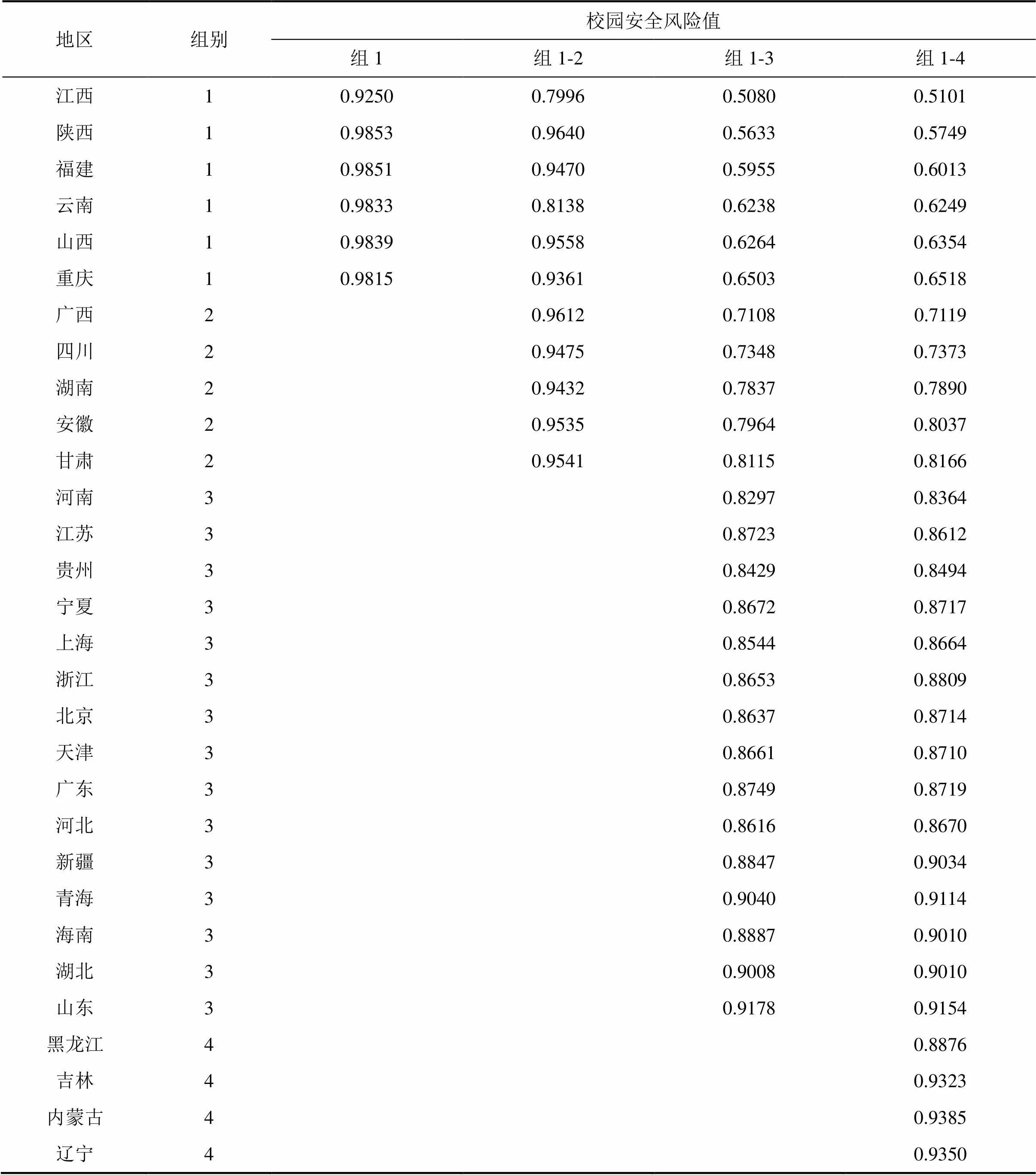
表4 基于分类Bootstrap-DEA模型的30个省份中小学校园安全风险测算值

四、校园设施安全的政策建议

校园作为社会的缩影，也时刻处于一种风险状态，校园设施安全事故的频繁发生，正是多种风险因素共同作用的结果。因此，预防校园设施安全应将我国校园设施安全从“被动式”管理转化为“主动式”安全风险管理，进行事前风险评估就显得尤为重要。本文构建的校园设施安全风险评估模型区别于传统的风险评估方法主要在于其以“效率为导向”。风险评估不是以校园设施安全发生率等产出指标来作为各地区中小学校园设施安全预防工作好坏的依据，而是以效率为导向，综合考量各地区中小学校园设施安全的投入产出比状况，以效率为宏观调控的“指挥棒”，推动中小学校园设施安全从“粗放型”预防向“精准性”预防转变，塑造出符合各地区实际情况的管理情境。根据以上的研究结论，提出以下几点政策建议。

第一，推广校园设施风险水平较低地区的安全防范经验。从本文的研究结论来看，这些经验的核心在于改变中小学校园学生密度过大、校园设施老旧以及校园安全经费投入不足等现状。“校园学生密度过大”说明该地区当前的学校资源有限，与学生需求之间的矛盾依旧突出，导致大量的学生拥堵在狭窄的空间，容易诱发学生群体因“小事”而惊慌失措，为校园设施安全埋下巨大的安全隐患。“校园设施老旧”说明这些风险水平较高的地区，未能对校园设施进行及时更新或者定期维护，导致校园设施经常出现如建筑物塌陷、体育设施零件脱落等现象，增大了校园设施安全事故爆发的可能性。“校园安全经费投入不足”说明该地区对中小学基础建设投入不足，主要通过培训校园安全管理人员和提高设施质量等方面来提高校园设施安全的预防能力。因此，预防中小学校园设施安全风险可以通过减少学生密度、及时更换或定期维护校园安全设施以及适当增加校园建设公共财政投入来提高校园设施安全预防能力。

第二，政府的公共财政投入既要重视地区间的平衡，也要注意各地区间的差异。在制定各地区中小学校园建设公共财政预算时，可综合考虑各地区的危房面积、学生密度以及校园设施安全事故发生率等因素，为处于相对无效状态的地区制定相应基准的安全预防目标，通过合理的分配政府预算额度，减少校园建设公共财政“投入”的冗余和“产出”的不足。对于风险值大于0.8的地区(如黑龙江、吉林、辽宁、内蒙古等)，此类地区的重点在于加强校园设施安全管理，利用有限的财政投入，创造出更低的“产出”效应，即更低的校园设施安全事故发生率。

第三，科学制定中小学校园设施安全短期、长期预防目标。本文通过分类DEA模型评估我国中小学校园设施安全风险，能有效地将处于同一风险水平的地区进行归类，有利于各地区根据自身实际情况，调整校园设施安全管理策略。一方面，与“低风险”的地区相比，虽然这些“高风险”的地区短时间达到“低风险”地区校园设施安全风险水平的可能性并不大，但是与同一类别中“最佳”风险水平的地区相比，仍具有短期提高的可能性。因此，这类地区应对比其与同一类别中“最佳”地区的差异，积极调整自身安全管理策略，以期短期实现同一类中的风险“最佳”。另一方面，处于“风险较高”水平的地区尽管在短期内能达到某一较低的安全风险水平，但长期而言，校园设施安全预防的最终目标是尽可能地降低校园设施安全事故率，减少损失。因此，这些地区在制定短期校园设施安全管理策略的同时，也应该不断地调整自身策略，朝着更长远的目标努力。

五、结语

传统的校园安全风险评估方法，其评估函数中的参数大都依赖于专家的经验、知识等，具有很强的主观性，因此很难对校园安全的风险水平进行定量测算。本文首次将DEA方法引入到校园安全风险的评估中，具有一定的开创性，克服了传统风险评估中指标间权重无法有效分配的问题。同时，针对经典DEA方法无法消除样本随机因素对风险测算结果的影响，引入Bootstrap方法对中小学校园安全风险测算结果进行修正。最后，针对各地区中小学校园设施安全风险水平的变差系数较大的情况，采用分类DEA模型对各类别中小学校园安全风险进行评估。主要结论和政策建议如下：①我国中小学校园设施安全风险整体相对较高，致使我国中小学校园设施安全事故频发，且我国中小学校园设施安全风险呈现出“东北地区＞东部地区＞中部地区＞西部地区”的特点；②采用Bootstrap-DEA方法对中小学校园设施安全风险测算值进行修正，其修正后的测算值相比于经典DEA模型测算的风险水平下降了7.2%左右；③运用分类DEA模型对各地区校园设施安全风险进行评估，有利于增加各地区校园设施安全风险水平的可比性，从而为各省(直辖市)的教育部门针对中小学校园设施安全风险管理提供防灾、减灾的科学依据。

注释：

① 表中第2列和第7列为经典DEA模型风险测算值；第3列和第8列为Bootstrap-DEA模型测算的风险修正值；第4、9列以及第5、10列分别为修正值置信区间的上下界(=0.05)；迭代此时设置为B=200,置信区间选为95%。

② 国家统计局公布最新校园安全相关数据为2013年版，本文主要侧重于风险评估方法的运用。

[1] 高山. 中国应急教育与校园安全发展报告[M]. 北京: 科学出版社, 2017: 126−127.

[2] 昆明明通小学踩踏事故: 26名受伤学生已出院18人[EB/OL]. http://jx.people.com.cn/n/2014/0929/c186330- 22484068.html.

[3] 家长质疑北京平谷六小塑胶跑道铲除不彻底校方称剩余部分另做处理[EB/OL].http://finance.people.com.cn/ n1/2016/0622/c1004-28470053.html.

[4] 冯帮. 论中小学校园突发事件风险的预防性评估[J]. 中国教育学刊, 2015(11): 67−72.

[5] 杨琼, 夏人青. 基于风险评估的学校教育社会风险管理构想[J]. 教育科学研究, 2011(8): 29−32.

[6] 方益权, 杜玉玉. 平安校园视域下社区安全风险评估制度研究[J]. 高等教育研究, 2014(7): 71−77.

[7] Zhang Y M, Xu Y. Application of fuzzy mathematics and comprehensive assessment in campus architecture safety assessment[J]. Applied Mechanics & Materials, 2011, 99/100(5): 1−9.

[8] 王起全. 中小学校园拥挤踩踏事故风险评估指标研究[J]. 中国安全科学学报, 2012(1): 149−156.

[9] 彭英, 唐刚, 位可娜. 学校体育场地设施对社会开放的安全风险规避研究[J]. 北京体育大学学报, 2017, 40(2): 79−86.

[10] Charnes A, Cooper W W, Rhodes E. Measuring the efficiency of decision making units[J]. European Journal of Operational Research, 1978, 2(6): 429−444.

[11] Shen Y, Hermans E, Brijs T, et al. Road safety risk evaluation and target setting using data envelopment analysis and its extensions[J]. Accident Analysis & Prevention, 2012, 48(3): 430−441.

[12] Cooper W W, Kingyens A T, Paradi J C. Two-stage financial risk tolerance assessment using data envelopment analysis[J]. European Journal of Operational Research, 2014, 3(1): 273−280.

[13] Li M, Lv J, Chen X, et al. Provincial evaluation of vulnerability to geological disaster in China and its influencing factors:a three-stage DEA-based analysis[J]. Natural Hazards, 2015, 79(3): 1−14.

[14] Simar, Wilson. Sensitivity analysis of efficiency scores: how to bootstrap in nonparametric frontier models[J]. Management Science, 1998, 44(1): 49−61.

[15] Heinrich H W, Petersen D, Roos N R. Industrial accident prevention: a safety management approach[M]. 1980: 89.

[16] 郝篆香, 蔡敏. 美国中小学安全教育的实施及其启示—以南卡罗来纳州为例[J]. 外国教育研究, 2011(11): 31−36.

[17] 程天君, 李永康. 校园安全:形势、症结与政策支持[J]. 教育研究与实验, 2016(1): 15−20.

[18] Schreck C J, Gibson C L, Miller J M. Trouble in the school yard:a study of the risk factors of victimization at school[J]. Crime & Delinquency, 2003, 49(3): 460−484.

[19] Riffe D, Others A. The effectiveness of random, consecutive day and constructed week sampling in newspaper content analysis[J]. Journalism Quarterly, 1993, 70(1): 133−139.

[20] Lewis H F, Sexton T R. Data envelopment analysis with reverse inputs and outputs[J]. Journal of Productivity Analysis, 2004, 21(2): 113−132.

[编辑: 胡兴华]

Campus facilities safety risk assessment research for primary and secondary schools: Based on DEA model

GAO Shan, LING Shuang

(School of Public Administration, Central South University, Changsha 410083, China)

The present essay took Bootstrap-DEA model and clustering analysis method to process the original data from 30 provinces (except Tibet, Taiwan and Hong Kong and Macao regions) to measure the campus security risk level. The conclusion was drawn as follows. In general, the safety risk of primary and secondary schools in China presented an overall pattern of Northeast>Eastern China>Central China>>West China, and there was great difference among 30 provinces about campus safety risk. It would be beneficial to promote the campus safety management mode of preventing accidents from the mode of “extensive pattern” to that of “precision pattern,” and the education departments of various regions also can set short-term and medium-and-long-term policy for the campus security management by accurately weighing the safety risk level of primary and secondary schools in China.

primary and secondary schools; campus facilities safety; risk assessment; Bootstrap-DEA model; cluster analysis

B82

A

1672-3104(2017)05−0152−08

2017−02−28；

2017−05−31

2016年国家自然科学基金项目“社会化媒体下重大决策社会稳定风险传导路径与防控机制研究”(71573280)；2016年国家自然科学基金项目“基于博弈论视角的我国食品行业监管模型与机制创新研究”(71573281)；2016年湖南省哲学社会科学基金西部项目“湘西地区文化旅游扶贫研究”(16YBX029)；2016年国家社科基金项目“大学生网络素养与社会主义核心价值观认同研究”(16CKS045)

高山(1969−)，男，湖南长沙人，管理科学与工程博士，中南大学公共管理学院教授，主要研究方向：风险管理，高教管理，政府绩效管理；凌双(1990−)，男，湖南衡阳人，中南大学公共管理学院博士研究生，主要研究方向：风险管理，绩效评估