农村征地冲突的RDEU鹰鸽博弈均衡分析

洪开荣，孙丹



农村征地冲突的RDEU鹰鸽博弈均衡分析

洪开荣，孙丹

(中南大学商学院，湖南长沙，410083)

将等级依赖期望效用理论模型与非对称鹰鸽博弈模型相结合，构建农村征地冲突的RDEU鹰鸽博弈模型，同时探讨心理情绪因素和非对称因素对博弈参与者行为策略的影响。研究表明，地方政府或农民的行为不仅受对方策略选择影响，还受情绪和非对称程度的影响。地方政府或农民越乐观，越倾向于和平解决冲突问题，地方政府或农民越悲观，越倾向于采取极端性对抗行为，且悲观情绪更容易影响地方政府或农民的行为抉择；而非对称程度越大，地方政府越倾向于采取强硬策略，农民越倾向于采取妥协策略。MATLAB的数值模拟情况进一步验证了这一结论，且为寻求可行性的冲突治理策略提供了参考方向。

农村征地冲突； RDEU理论；非对称鹰鸽博弈；情绪函数；纳什均衡

一、引言

伴随着新型城镇化进程的加快，政府征用农村土地的数量持续增加、规模不断扩大。农村征地冲突已经成为农村突发性群体性事件的主要表现形式[1]。从吉林龙潭区城管队长被砍死的血腥事件到昆明晋宁县施工方疯狂袭击村民的恶性行为再到保定白沟镇的“11·16”暴力征地事件[2−4]，农村征地冲突事件频繁发生，严重威胁着人民的财产与生命安全，影响着社会的稳定。

近年来，国内外的研究学者针对农村征地冲突的影响因素进行了研究。国外学者Campbell、Alston、Andrew和Kirabo等针对农村征地冲突的原因进行多重分析，研究成果大致归纳为宏观层面的综合原因、中观层面的土地权属问题以及微观层面的具体诱因这三个方面[5−8]。国内学者祝天智、霍有光等对我国农村征地冲突影响因素的关注主要聚焦在公共利益与产权归属、政策漏洞与制度缺陷、乡村治理等问题上[9−10]。但是，就目前来看，国内外学者对农村征地冲突中情绪因素和非对称因素的关注较少。征地类群体性事件的发生是一个从冲突积累到冲突激化再到冲突缓解的不断演变过程[11]，部分学者从博弈论视角，探讨了地方政府与失地农民之间的利益博弈，并提出了改革土地征收补偿制度等治理建议[12−14]。但目前对博弈论方法的应用以行为博弈、演化博弈分析为主，较为单一，与其他理论视角的结合较少。

作者认为，农村征地冲突事件中的主要参与主体——地方政府官员和农民作为社会中的人，其行为必定会受到情绪的影响，且其情绪也会影响或扩散到其他人。除此之外，博弈主体之间的实力差距也会对征地冲突产生影响。等级依赖期望效用理论(rank dependent expected utility，简称RDEU)是一种考虑了情绪参数的效用理论[15−17]，而非对称鹰鸽博弈模型恰巧是一种考虑了非对称因素的经典博弈模型[18−19]，因此，本文将RDEU理论模型与非对称鹰鸽博弈模型相结合，构建同时包含情绪因素和非对称因素的农村征地冲突综合模型，并将其称之为“RDEU鹰鸽博弈模型”。在此基础上，通过RDEU鹰鸽博弈均衡分析，探寻情绪和非对称程度对征地冲突的影响情况，并利用MATLAB软件进行模拟分析，验证模型的实用性。

二、理论依据

RDEU理论是由Quiggin[16]在探究EU理论局限性的根源、引入风险因素并通过对其无差异曲线发散现象进行修正时而提出的，并且得到了Schmeidler、Diecidue和Wakker、Levy、Karni和Schmeidler等学者的进一步验证和完善[20−23]。该理论结合(逆)累积概率而非单纯概率的方法来引入非线性函数定义决策权重，在EU理论模型的基础上构建了等级依赖期望效用模型。

(一) RDEU理论模型

定义1[16−18]：如果随机变量取值于集合{x,=1, 2,…,}，规定1>2­>…>x，且服从概率分布

Pr{=x}=P,=1, 2, …,(1)

满足p≥0，1+2+…+p=1,则对x定义其秩位(ranking position，简记为RP)为：

RP=Pr{≤x}=p+p+1+…+p,=1, 2,…,(2)

定义2[16−18]：在不确定性决策结构下，决策者满足RDEU决策模型是指，他的偏好序“≻”可以用由效用函数()和决策权重定义的实值函数来表示，即对随机变量、：

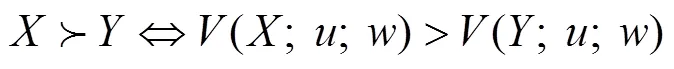
其中：

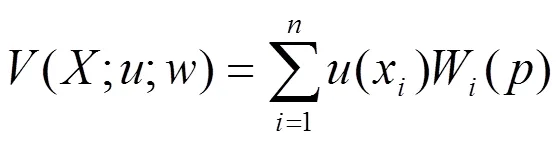
这里，W() 是x的决策权重(基于秩)，定义为：

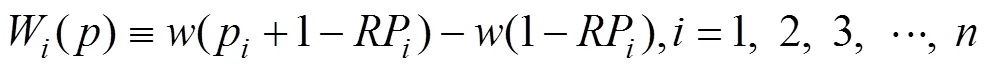
F为(·)，通常被视为决策者的情绪函数，且满足条件：(0)=0，(1)=1，单调递增。当()>时，即为凹函数，反映决策者的悲观情绪；当()<时，即为凸函数，反映决策者的乐观情绪；当()=时，决策者不受情绪影响。

(二) RDEU博弈模型

设在人非合作博弈中，博弈方的混合策略是定义在策略组合x={1(i),2(i),…,x(i)}上的一个概率分布[24]：

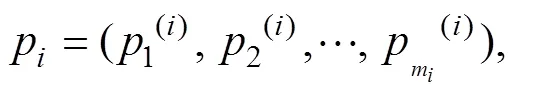
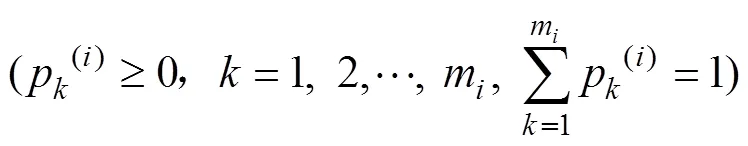
其混合策略集为：

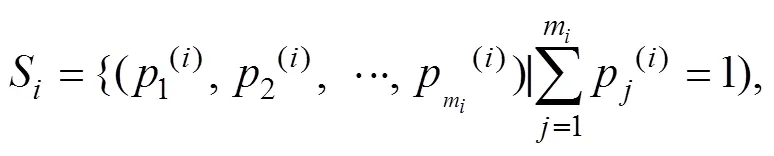
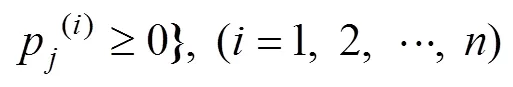
当每个博弈方选定一个混合策略：p=(1(i),2(i), …,p(i)) (=1, 2,…,)后，博弈所形成的一个混合局势记为：=(1,2,…,p)，博弈方在一个混合局势下的效用函数为u(1,2,…,x)。

设博弈方的情绪函数为F=(·)，记：

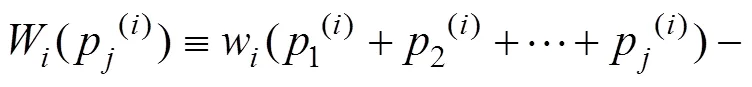
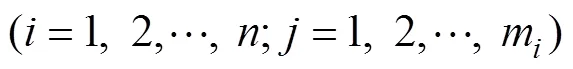
这样，根据RDEU理论模型，在混合策略=(1,2, …,p)下，博弈方的RDEU期望效用函数为：

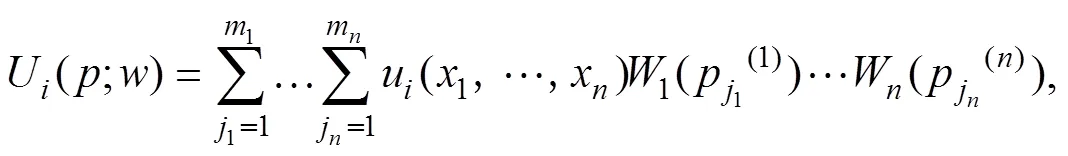
定义3[24]：用数学模型=[, {S}, {U}]表示的博弈称为RDEU博弈模型。其中，为博弈方集合，S为博弈方的混合策略集，U为博弈方的期望效用函数。

在实际应用中，为表述方便，式(8)可以记为：

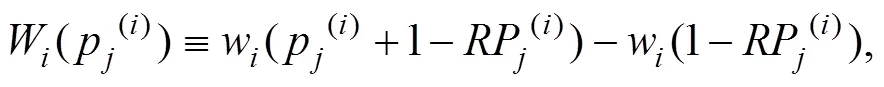
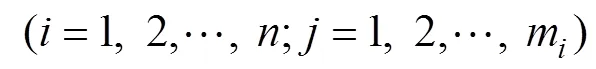
其中：RP(i)=p(i)+p+1(i)+…+p(i)称为x的秩。

三、农村征地冲突的RDEU鹰鸽博弈模型构建

农村征地冲突的RDEU鹰鸽博弈模型就是将RDEU博弈模型与非对称鹰鸽博弈模型相结合的综合模型。在现实的征地冲突博弈中，失地农民在权利、信息、心理、能力等方面明显处于劣势地位，其权益常常受到侵害[25]。正是由于失地农民和政府官员都是明显有差别的非对称有限理性博弈群体，双方的冲突处于非对称信息博弈状态中，因此，我们才首先构建农村征地冲突的非对称鹰鸽博弈模型。

(一) 未引入RDEU理论的冲突博弈

假设1：模型中，定义=/1−为非对称因子，用来衡量地方政府与农民之间的非对称程度。假设官员与农民实力总和为1，为政府官员实力比重，1−为农民实力比重，通常前者大于后者。在现实情况中，政府官员无论在权利掌控上还是在信息把握上都明显地强于处于弱势地位的农民，因此，非对称因子始终大于1。

假设2：地方政府与农民在争夺土地收益时，对同一块土地效用价值的认知存在偏差。模型假设政府官员从一次征地中获得的直接经济收益为，农民从中获得的直接经济收益为，且＞0，冲突成本为。如果=，=1/2，那么博弈模型就会回归到传统的对称性鹰鸽博弈模型。

该博弈中，如果双方都采取攻击型(鹰)策略，则地方政府的收益为()/4①，农民的收益为()/4(1)。如果双方都采用和平型(鸽)策略，则博弈双方均可规避冲突带来的风险成本()，政府收益为kV，农民收益为(1)。如果地方政府采取攻击型(鹰)策略，农民采取和平型(鸽)策略，则地方政府获得收益，农民无收益。如果农民采取攻击型(鹰)策略，地方政府采取和平型(鸽)策略，则农民获得收益，地方政府无收益。见表1。

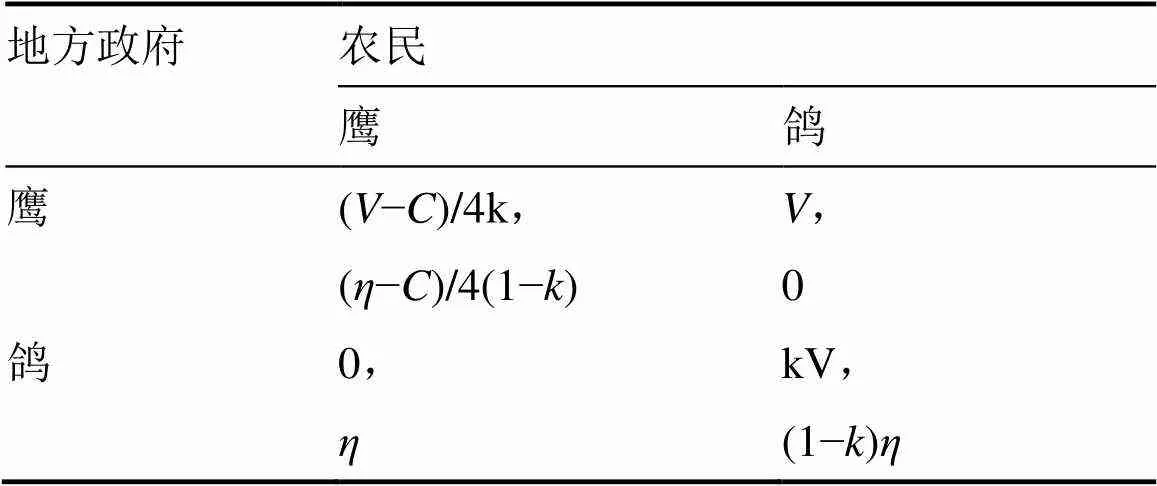
表1 农村征地冲突的非对称鹰鸽博弈模型

根据现实情况，双方都采取强硬策略时，会给社会带来负收益，冲突成本远超过双方的心理期望收益，即，(−)/4＜0，(−)/4(1−)＜0。对地方政府来说，{鹰，鸽}＞{鸽，鸽}＞{鸽，鹰}＞{鹰，鹰}；对农民来说，{鸽，鹰}＞{鸽，鸽}＞{鹰，鸽}＞{鹰，鹰}。依次有如下参数之间的关系：

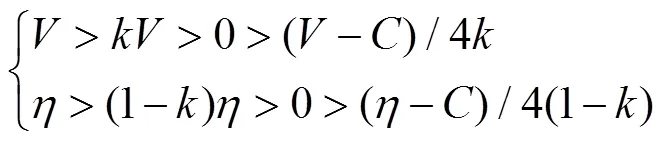
由此得到，该利益博弈的纯策略纳什均衡为(鹰，鸽)和(鸽，鹰)，其现实意义表明，当博弈双方均完全理性，一方采取攻击型强硬策略时，另一方出于自身利益最大化考虑，只能无奈妥协。所以，只要博弈均衡结果不是(鸽，鸽)策略组合，冲突可能性就会存在，那么征地补偿的利益分配就是不公平的。但是，博弈双方在信念策略互动过程中，彼此的情绪状态究竟是如何影响博弈决策的呢？从上述博弈参与方的简单效用函数中，难以察觉博弈方的心理活动对其行为策略选择的积极或消极影响情况；除此之外，在一般的非对称鹰鸽博弈模型中，单纯地研究非对称因子对博弈决策的影响也显得苍白无力(博弈方情绪影响博弈主体对非对称程度的信念认知)。因此，还需要将博弈方的心理状态体现在效用函数中。

(二) 引入RDEU理论的冲突博弈

本文将农民与地方政府的情绪状态划分为乐观、理性与悲观三个维度，且假设参与方的情绪状态随机组合（这里的理性情绪状态指的是参与者行为策略选择不受情绪影响的一种理想状态）。另外，假设地方政府采取鹰策略的概率为，农民采取鹰策略的概率为。为将博弈双方行为决策时的情绪态度反映在模型中，本文定义地方政府的情绪函数为w()=p1，1为地方政府群体的情绪指数，且满足1＞0；农民的情绪函数为w()=q2，2为农民群体的情绪指数，且满足2＞0。

根据RDEU博弈模型，结合征地冲突的非对称鹰鸽博弈模型(见表1)，可分别得到地方政府群体、农民群体获得相应收益时的概率分布律、相应收益的秩位以及相应收益的决策权重，如表2、表3所示。

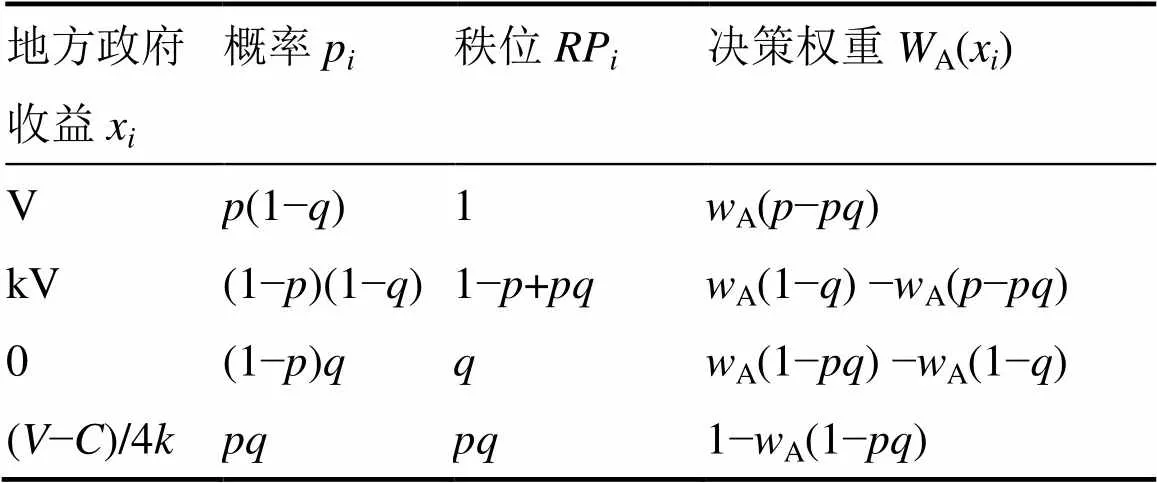
表2 地方政府群体收益值对应的概率分布、秩位及决策权重

表3 农民群体收益值对应的概率分布、秩位及决策权重

由此得到，地方政府群体对应的RDEU期望效用函数为：

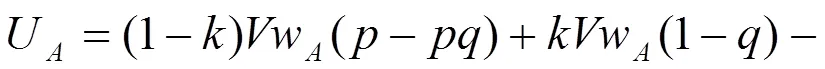
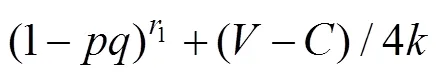
农民群体对应的RDEU期望效用函数为：

U=kηw(−)+(1−)ηw(1−)−

[(−)/4(1−)]w(1−)+(−)/4(1−)

=(−)2+(1−)(1−)2−

[(−)/4(1−)](1−)2+(−)/4(1−) (12)

四、农村征地冲突的RDEU鹰鸽博弈均衡解

在以上模型构建中，我们借助RDEU理论引入情绪函数，从而改变了参与主体传统的效用函数。在此基础上，我们将进一步求解以上农村征地冲突RDEU鹰鸽博弈模型的纳什均衡解，并探讨博弈参与者情绪对其行为决策的影响。

(一) 纳什均衡

借鉴一般纳什均衡的定义，给出RDEU鹰鸽博弈模型的纳什均衡定义，即：

定义4[15]：征地冲突的RDEU鹰鸽博弈模型=[, {S}, {U}]中,若存在混合策略(*，*)，使得以下不等式关系同时成立，即：

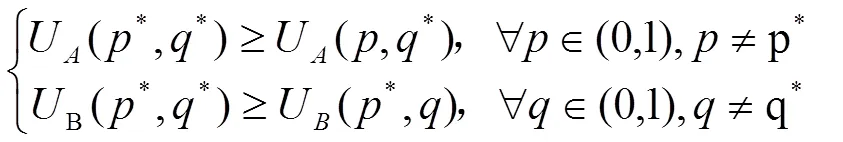
则称(p，q)为博弈的混合策略纳什均衡。

(二) 均衡解分析

按照纳什均衡求解的基本逻辑，当地方政府群体和农民群体都采取混合策略，即,∈(0, 1)时，分别对两群体对应的RDEU期望效用函数即式(11)和式(12)求偏导得：

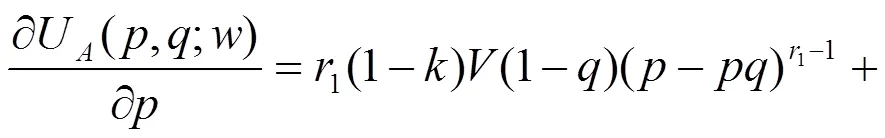
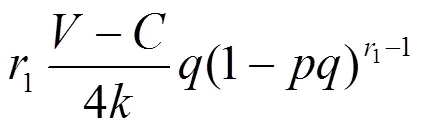
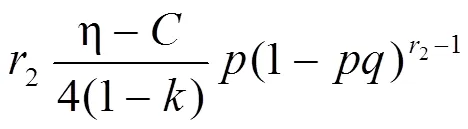
农村征地冲突RDEU鹰鸽博弈模型的混合策略纳什均衡解需同时满足以下条件：

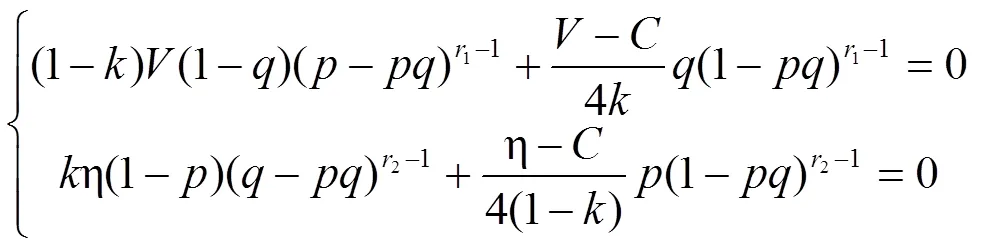
针对超越方程组式(15)的求解问题，通常分类别进行讨论。这里，我们根据博弈方的不同情绪状态，从以下三种典型情况分别进行探讨。

情况１：双方无情绪。

这种情况下，地方政府群体和农民群体都是完全理性群体，其行为策略抉择完全不受情绪干扰，即1=1,2=1,A()=,B()=。将1=1,2=1代入超越方程组，进而得到地方政府群体的混合策略为：

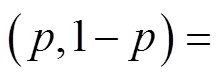
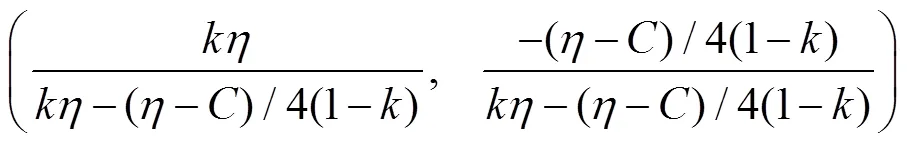
农民群体的混合策略解为：

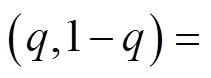
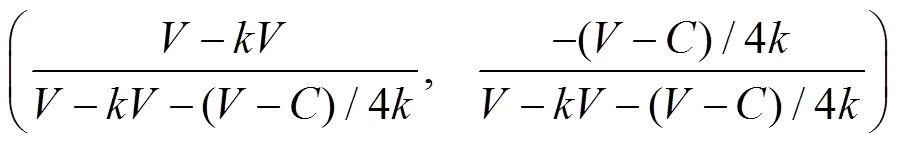
在1=1,2=1的假设条件下，混合策略的纳什均衡解为：

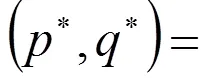
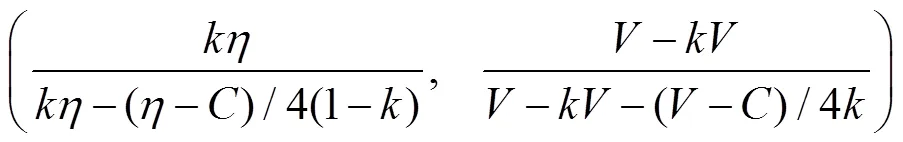
由于这种情况与传统博弈理论的假设完全吻合，所以均衡结果与一般博弈的混合策略纳什均衡解完全相同。但是，在现实征地冲突中，完全理性的状态极其少见，博弈方尤其是弱势群体易受自身和外界因素影响而使其策略选择带有少许个人情绪甚至极端化个人情绪。

情况2：一方有情绪。

这种情况下，假设地方政府理性但农民具有情绪（农民理性而地方政府不理性的状态在现实中几乎不存在），即1=1，2≠1，A()=，B()≠。处于管理者地位的地方政府群体为了完成征地任务，往往会压制自己的情绪，基本符合理性人的假设。而处于弱势地位的农民群体由于获取社会物质资源、信息资源等方面的能力不足，且在征地事件中利益诉求表达受阻，易在决策时带有个人情绪甚至采取极端化的方式与政府抗争。

农民群体有时会对未来预期收益持“乐观”态度，有时会持“悲观”态度。

第一，假设地方政府群体符合完全理性人的假设，农民群体对未来预期收益持“乐观”态度。那么，这时地方政府完全无情绪，即1=1；农民群体的情绪函数B()为凸函数，即2＞1。

农民群体的“乐观”情绪由有限理性完全转换为无理性状态时，有1=1，2→+∞。比如农民群体对利益、公平的感知持极度乐观态度甚至“自以为是”地认为政府一定会采取“鸽”策略而使自身获得的最终利益补偿达到其心理预期值，这一极端化的信念认知诱使其行为抉择逐渐向“鸽”策略靠近。结合式(15)，进而有以下推导关系：

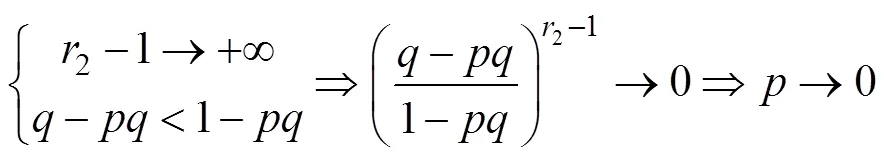
于是得到，农民群体采取鹰和鸽的混合策略为：

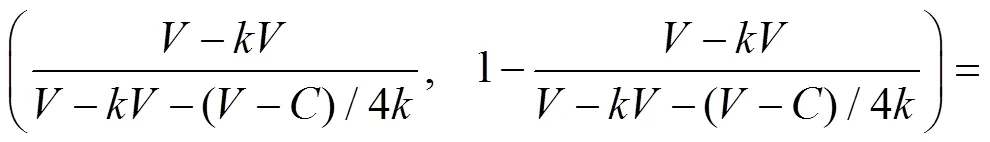
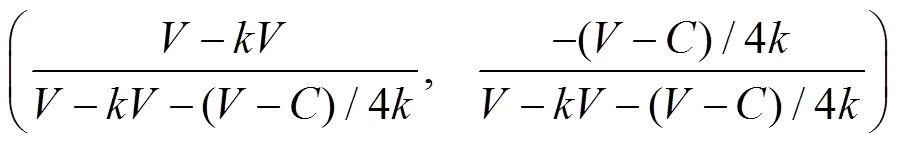
而地方政府群体采取鹰和鸽的混合策略为：

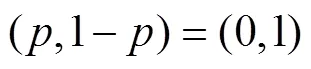
因此，混合策略纳什均衡解为：

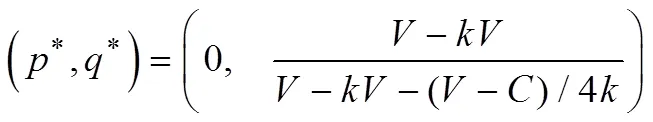
以上混合策略纳什均衡解表明，当政府无情绪、农民持有极端化乐观情绪时，地方政府群体完全选择“鸽”策略，农民群体则以一定比例选择“鸽”策略。这一结果与双方均无情绪时的纳什均衡解相比，博弈结果更加逼近和平策略组合（即双方均选择“鸽”策略）。

第二，假设地方政府群体符合完全理性人的假设，农民群体对未来预期收益持“悲观”态度。那么，这时地方政府完全无情绪，即1=1；农民群体的情绪函数B()为凹函数，即0＜2＜1。

农民群体的“悲观”情绪由有限理性完全转换为无理性状态时，有1=1，2→0。比如农民群体对利益、公平的感知持极度悲观态度以至于农民群体完全不信任政府，认为即便自身反对征收，政府也会无情地实行强征，对公平补偿不报任何希望，这一极端化的信念认知引导其行为抉择逐渐向“鹰”策略靠近。结合式(15)，进而得到：

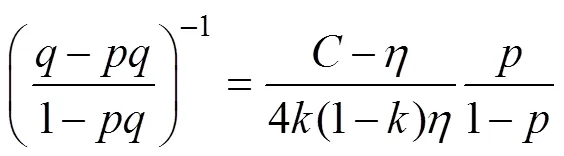
求解方程，得到农民群体采取鹰和鸽的混合策 略为：

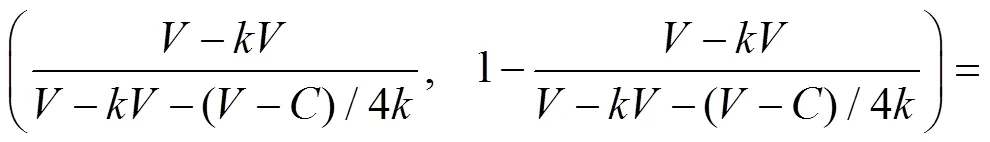
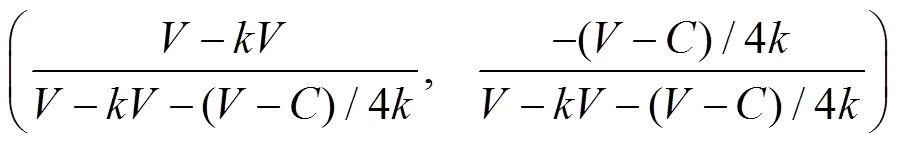
地方政府群体采取鹰和鸽的混合策略为：

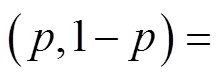
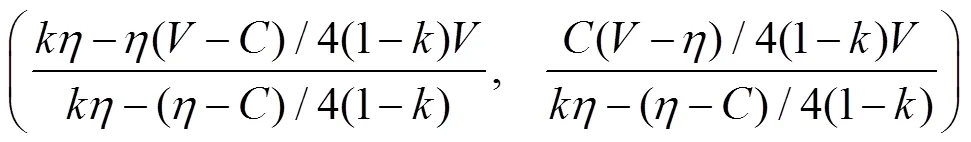
因此，混合策略纳什均衡解为：

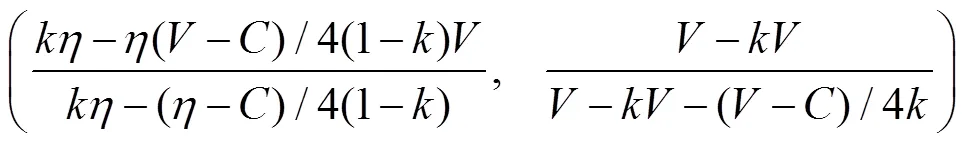
以上混合策略纳什均衡解表明，当政府无情绪、农民持有极端化悲观情绪时，农民群体以一定比例选择“鸽”策略，上一种情况中所述原本百分之百选择“鸽”策略的政府群体则有部分发生动摇转而选择“鹰”策略。这一结果与双方均无情绪时的纳什均衡解相比，博弈结果更加逼近抗争策略组合（即双方均选择“鹰”策略）。

情况3：双方有情绪。

这种情况下，假设地方政府群体和农民群体都是带有情绪的有限理性群体，双方都具有情绪，即1≠1,2≠1,A()≠,B()≠。现实冲突中，不仅农民会带有情绪，处于代理人地位的地方政府官员有时也会因追求自身利益最大化，与土地开发商相互勾结发生寻租行为从而失去理性，这就会导致其在征地活动中带有情绪。因此，我们得到地方政府群体相应的反应函数为：

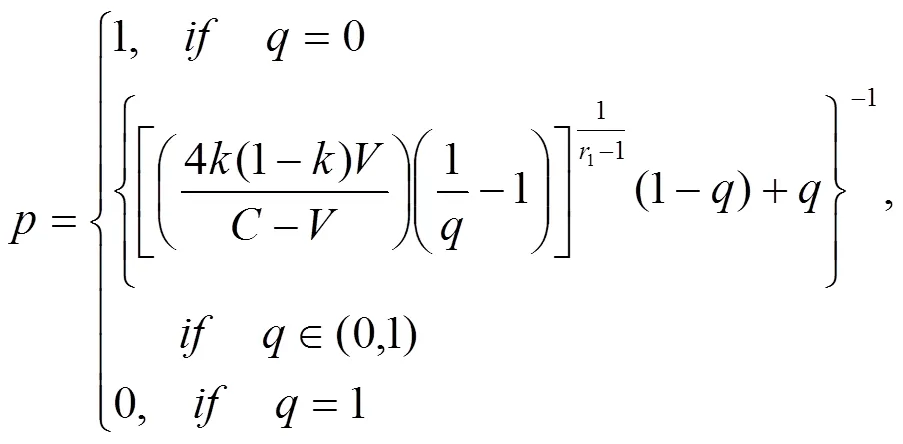
农民群体相应的反应函数为：

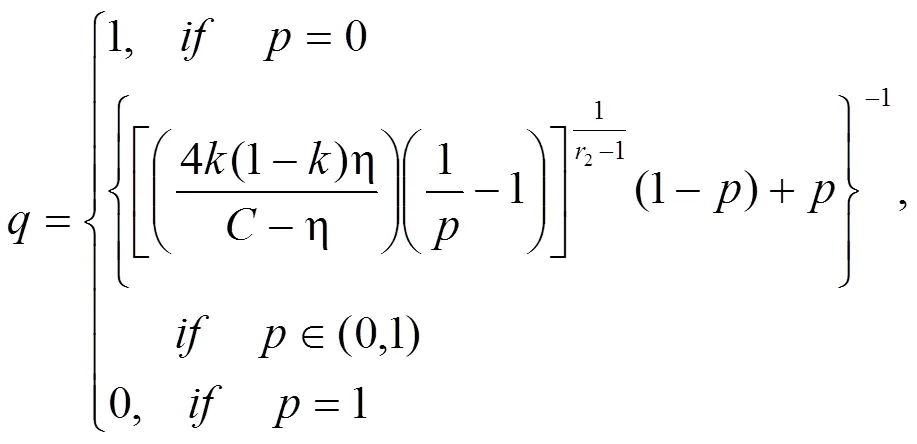
为了研究方便，将博弈方的行为策略看作1、2的函数，并分别记为(1)和(2)。然后进一步通过对(1)和(2)一阶导数的分析，来获取不同的情绪指数1、2对(1)和(2)的具体影响情况。

经计算，(1)和(2)的一阶导数分别为：

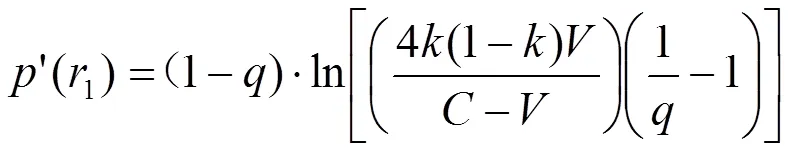
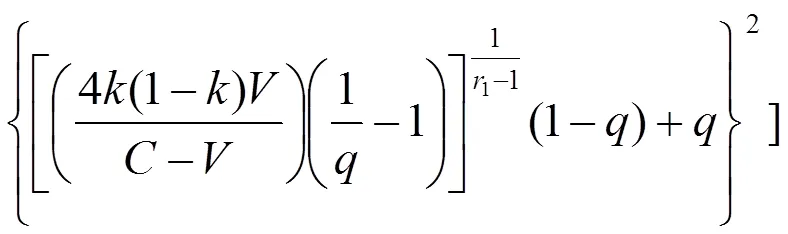
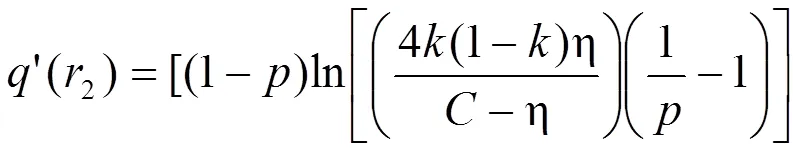
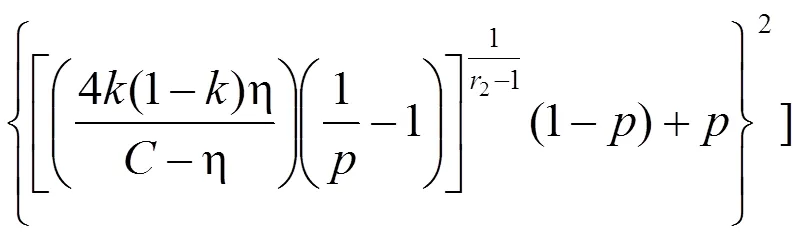
现在讨论式(27)的正负问题。由于在该式中，分母显然为零，且根据博弈模型已知的假设条件知，4(1−)/(−)＞0，因此，(1)的一阶导数′(1)的正负问题就直接转化成了讨论{[4(1−)/(−)][(1/) −1]}与“1”的大小关系问题。

第一，当＜4(1−)/[−+4(1−)]时，′(1)在区间(0, 1)和(1，+∞)上始终大于0，即当农民群体采取“鹰”策略的概率小于临界值4(1−)/[−+ 4(1−)]时，其情绪函数(1)为情绪指数1的增函数。随着越来越小，农民群体采取“鸽”策略的概率越来越大时，地方政府群体会变得越来越乐观，愈发相信农民群体不会据理力争而做“钉子户”，为了获得更多收益，地方政府行为选择会越来越倾向于强硬的“鹰”策略，即(1)越来越大。因此，在信念互动和策略互动的反复作用中，博弈均衡会逐渐向(鹰，鸽)策略靠近。

第二，当＞4(1−)/[−+4(1−)]时，′(1)在区间(0, 1)和(1，+∞)上始终小于0，即当农民群体采取“鹰”策略的概率大于临界值4(1−)/[−+ 4(1−)]时，其情绪函数(1)为情绪指数1的减函数。随着越来越大，农民群体采取“鸽”策略的概率越来越小时，地方政府群体会变得越来越悲观，不再相信农民群体愿意和平地配合征地行为，为了避免遭受更多损失，地方政府行为选择会越来越倾向于强硬的“鹰”策略，即(1)越来越大。因此，在信念互动和策略互动的反复作用中，博弈均衡会逐渐向(鹰，鹰)策略靠近。

第三，当=4(1−)/[−+4(1−)]时，′(1)在区间(0, 1)和(1，+∞)上恒等于0，即当农民群体采取“鹰”策略的概率等于临界值4(1−)/[−+ 4(1−)]时，农民群体的行为策略选择不再随情绪指数的变化而改变。此时，地方政府群体在信念策略互动思维的影响下，会相信并参考农民群体确定的策略选择概率，来确定自己对应的策略选择。

同理，对式(28)做同样的分析，即可得到以下三种情况：

第一，当＜4(1−)/[−+4(1−)]时，′(2)在区间(0, 1)和(1，+∞)上始终大于0，即当地方政府群体采取“鹰”策略的概率小于临界值4(1−)/[−+4(1−)]时，其情绪函数(2)为情绪指数2的增函数。随着越来越小，地方政府群体采取“鸽”策略的概率越来越大时，农民群体会变得越来越乐观，愈发相信地方政府群体为了完成征地任务会做出妥协，为了争取更多收益，农民群体的行为选择会越来越倾向于强硬的“鹰”策略。因此，在信念互动和策略互动的反复作用中，博弈均衡会逐渐向(鸽，鹰)策略 靠近。

第二，当＞4(1−)/[−+4(1−)]时，′(2)在区间(0, 1)和(1，+∞)上始终小于0，即当地方政府群体采取“鹰”策略的概率大于临界值4(1−)/[−+4(1−)]时，其情绪函数(2)为情绪指数2的减函数。随着越来越大，地方政府群体采取“鸽”策略的概率越来越小时，农民群体会变得越来越悲观，不再相信地方政府群体愿意提供公平补偿或预期补偿，为了避免遭受更多损失，农民群体的行为选择会越来越倾向于强硬的“鹰”策略。因此，在信念互动和策略互动的反复作用中，博弈均衡会逐渐向（鹰，鹰）策略靠近。

第三，当=4(1−)/[−+4(1−)]时，′(2)在区间(0, 1)和(1，+∞)上恒等于0，即当地方政府群体采取“鹰”策略的概率等于临界值4(1−)/[−+ 4(1−)]时，农民群体的行为策略选择不再随情绪指数的变化而改变。此时，农民群体在信念策略互动思维的影响下，会相信并参考地方政府群体确定的策略选择概率，来确定自己对应的策略选择。

综上所述，在整个征地冲突的非对称鹰鸽博弈中，地方政府群体和农民群体会互相参考依赖于对方的行为决策，并在自身心理情绪的影响下，随时变换自己的行为决策，以期达到获得更多收益或减少损失的 目的。

五、数值分析

为了进一步考察模型的性质和实用性，下面通过MATLAB数值模拟不同情况下的影响状况。这里，将征地冲突RDEU博弈模型中各要素的虚拟变量具体化为真实数值，假设地方政府群体的实力是农民群体实力的3倍，即=3，=3/4，并令=8，=6，=10。根据前面建立的博弈收益矩阵中各要素之间的大小关系，得到：

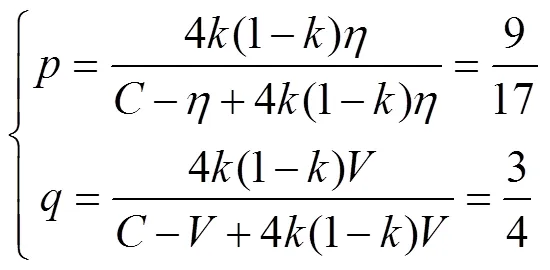
以下将在博弈双方都带有情绪的假设前提下，分别绘制博弈方自身情绪指数和另一方行为决策的变化对一博弈方行为决策影响的三维示意图。

(一) 地方政府群体受自身情绪和对方策略影响的情况

地方政府群体行为同时受情绪1和农民行为的影响情况，分地方政府“悲观”和“乐观”两种情况，如图1和图2所示。

由图1可知，在地方政府群体持有“悲观”情绪，即在r1∈(0, 1)的情况下，地方政府获得农民群体选择“鹰”策略的概率必定小于3/4的心理认知时，其自身采取“鹰”策略的概率随着其自身情绪指数1的增大而增大，而且当农民群体选择“鹰”策略的概率越来越小时，增长的速度会异常加快，如图1所示，随着逐渐减小，的增长幅度变得异常陡峭；相反，当地方政府获得农民群体选择“鹰”策略的概率必定大于3/4的心理认知时，随1的增大而减小，而且越大，减小的速度越来越快。如图1所示，随着逐渐增大，很快降为0。

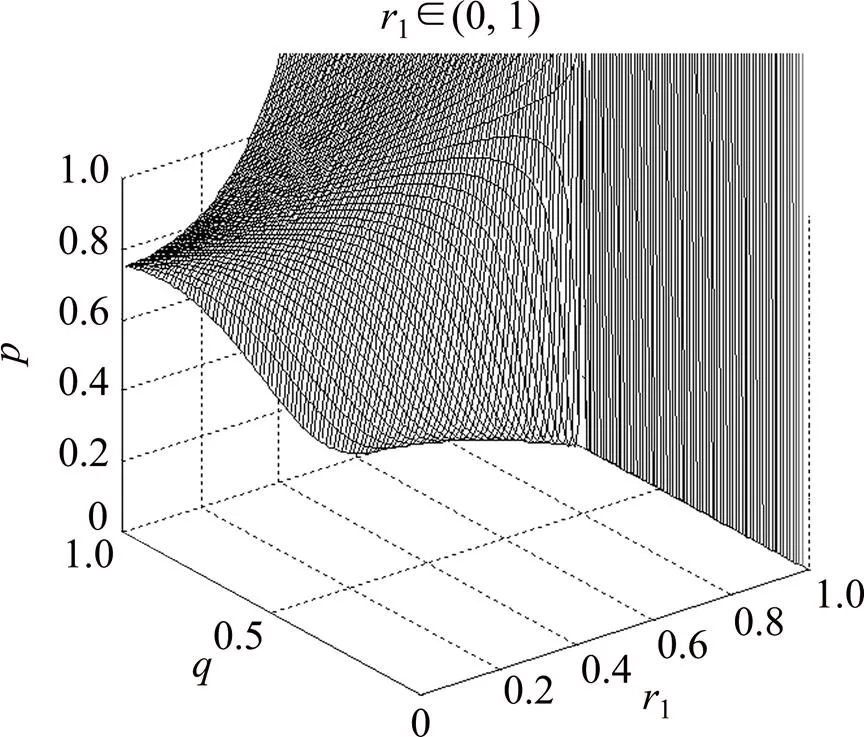
图1 地方政府决策p同时受q和“悲观”情绪r1影响的三维示意图

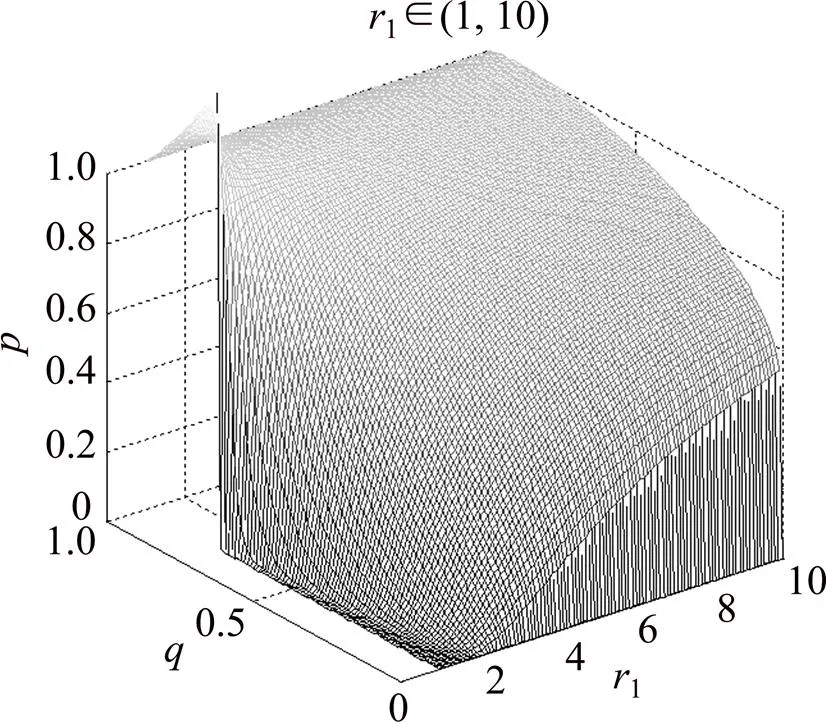
图2 地方政府决策p同时受q和“乐观”情绪r1影响的三维示意图

由图2可知，在地方政府群体持有“乐观”情绪，即在1∈(1,10)②的情况下，地方政府采取“鹰”策略的概率随和“乐观”情绪1的变动情况与1∈(0,1)情形下的变动情况类似。但不同的是，从图1和图2的对比来看，“悲观”情绪对地方政府的影响比“乐观”情绪对地方政府的影响更大。当小于3/4时，随着1增大而增大，且越小，增长的速度越快，但是这种增长速度与1∈(0,1)情况下（其他条件一样）的增长速度相比，不明显；同样，当大于3/4时，随着1增大而减小，且越大，减小的速度越快，但是这种减少速度明显慢于1∈(0, 1)情况下的减少速度，而且，在图2中只出现微小的驼峰，并未出现像图1中那样非常陡峭的纵剖面。

(二) 农民群体受自身情绪和对方策略影响的情况

农民群体受自身情绪和对方策略的影响状况与地方政府群体的情况相似，通过分析可以得到与地方政府群体类似的结论。具体情况见图3和图4，不再重复论述。

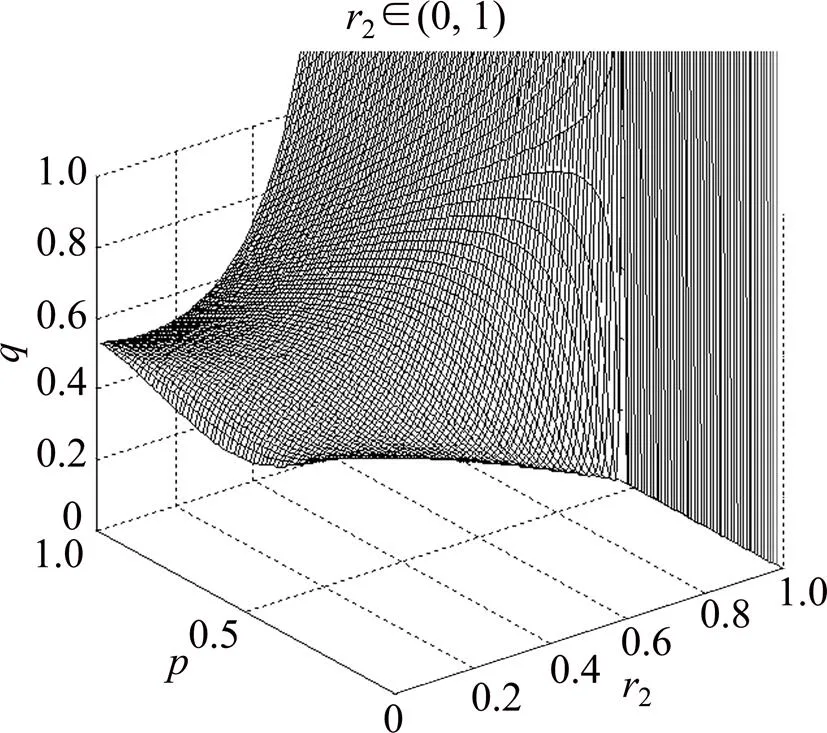
图3 农民决策q同时受p和“悲观”情绪r2影响的三维示意图

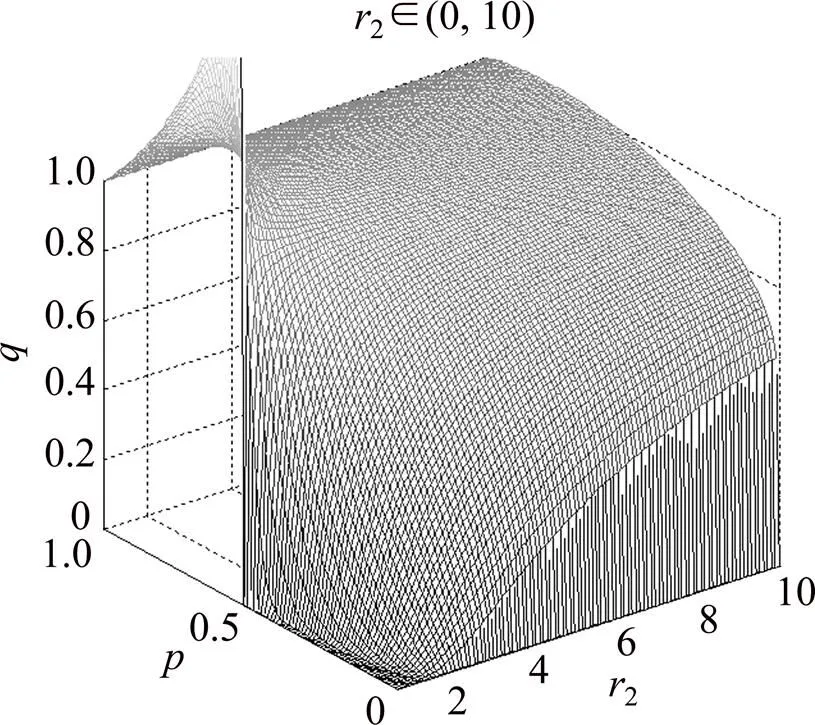
图4 农民决策q同时受p和“乐观”情绪r2影响的三维示意图

(三) 非对称因子对双方策略选择的影响

在现实的冲突博弈中，大多数情形下，地方政府群体持有“乐观”态度，而处于弱势地位的农民群体往往持有“悲观”态度。因此，这里将在“1＞1， 0＜2＜1”的假设前提下讨论非对称因子对双方策略选择的影响程度。

首先，讨论非对称因子对地方政府策略选择的影响情况。令=8，=6，=10，1=3，=3/4，并结合式(25)，运用MATLAB软件得到相应的二维示意图，见图5。

从图5可以看出，当政府实力＜0.5，即非对称因子＜1时，地方政府群体选择强硬性的“鹰”策略的概率随着政府实力的增加而减小，且减小的幅度越来越慢；当政府实力＞0.5，即非对称因子＞1时，地方政府群体选择强硬性的“鹰”策略的概率随着政府实力的增加而增大，且增大的幅度越来越快。

类似地，模拟非对称因子对农民策略选择的影响情况。令=8，=6，=10，2=0.5，=3/4，并结合式(26)，得到相应的二维示意图，见图6。

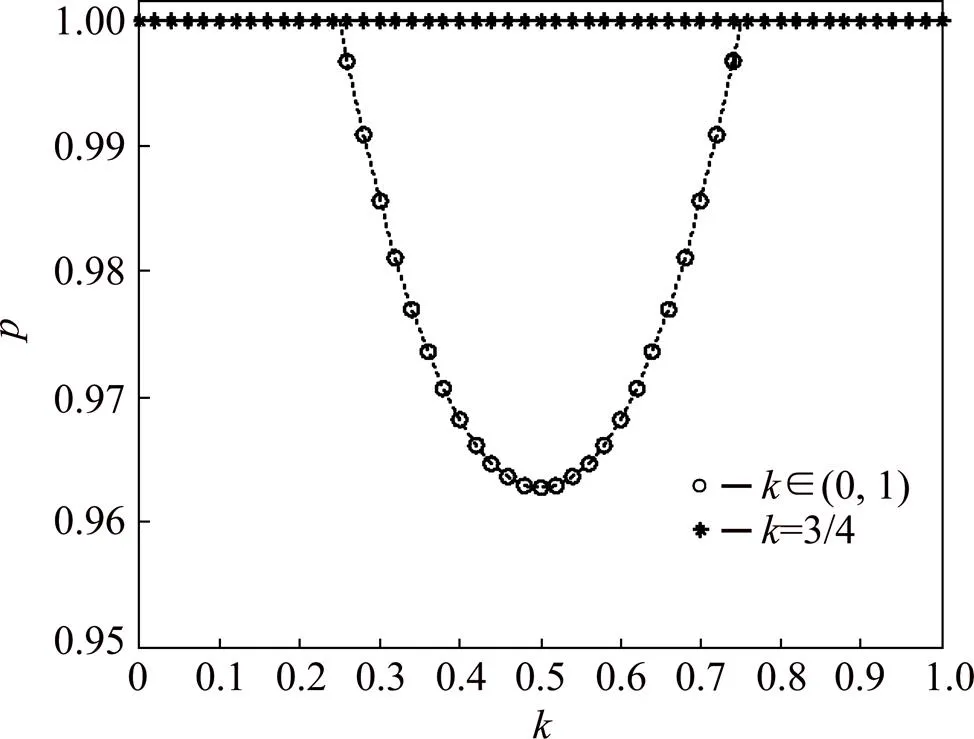
图5 地方政府决策受政府官员实力影响的二维示意图

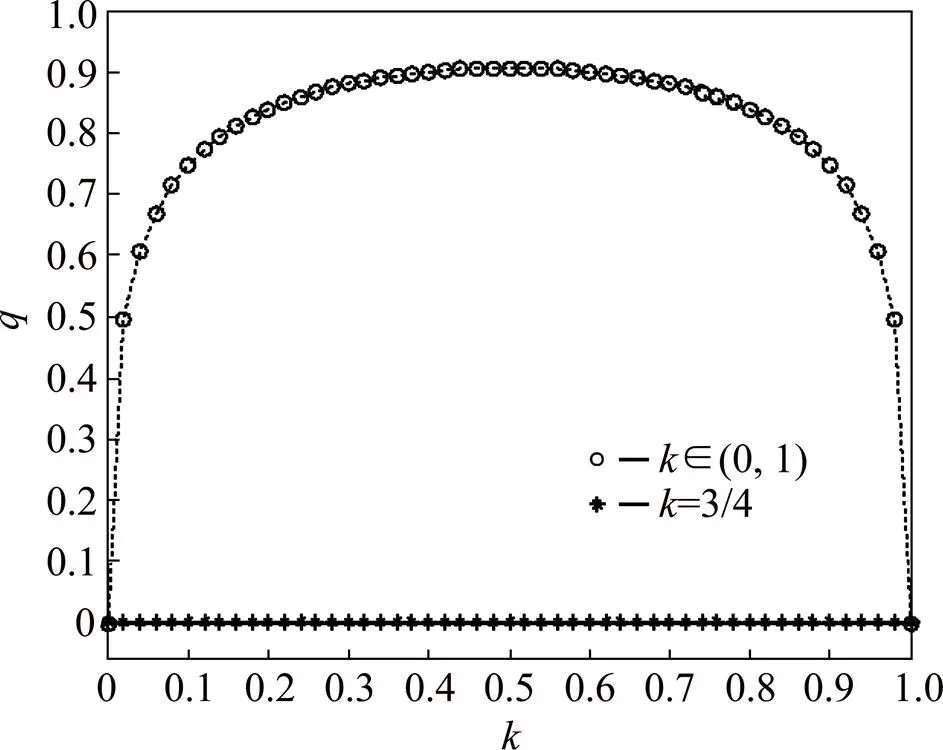
图6 农民决策受政府官员实力影响的二维示意图

从图6可以看出，当政府实力＜0.5，即非对称因子＜1时，农民群体选择强硬性的“鹰”策略的概率随着政府实力的增加而增大，且增大的幅度越来越小；当政府实力＞0.5，即非对称因子＞1时，农民群体选择强硬性的“鹰”策略的概率随着政府实力的增加而减小，且减小的幅度越来越大。

在现实的农村征地冲突事件中，弱势的农民群体往往由于利益诉求表达受阻或者得不到公平补偿而过于情绪化，以至于采取“跳楼”“自焚”等极端化的抗争方式使得冲突发生或恶化。大部分农民群体具有这样的认知：无论如何努力，都无法在短时间内改变自身在信息、权利、金钱等方面的劣势，极端化的斗争只会给自己带来更多损失甚至家破人亡。因此，当政府与农民之间的实力悬殊较大时，农民也只能在斗争中无奈妥协。假设政府实力是农民实力的3倍，非对称因子=3，即=3/4，如图5和图6所示，地方政府选择“鹰”策略，农民选择“鸽”策略时，补偿利益大部分流向地方政府。换句话说，当地方政府异常强硬时，即使农民反对，最终也会迫于政府压力而无奈接受强征。总之，非对称因子越大，地方政府越倾向于采取风险型的强硬策略，而农民群体则越倾向于采取保守型的妥协策略。

六、结语

在构建农村征地冲突RDEU鹰鸽博弈模型的基础上，本文进行了模型的均衡解分析以及MATLAB数值分析。主要得出如下几点结论：（1）地方政府（或农民）的情绪状态不仅影响其自身的行为策略选择，而且影响对方的行为策略选择，进而影响农村征地冲突RDEU鹰鸽博弈模型的均衡状态。（2）地方政府（或农民）在“乐观”情绪状态下，更倾向于选择和平解决冲突问题；地方政府（或农民）在“悲观”情绪状态下，更倾向于选择极端对抗恶化冲突问题。且地方政府（或农民）的“悲观”情绪状态较之其“乐观”情绪状态更易影响其自身及对方的行为策略选择。（3）非对称程度会影响冲突博弈的均衡状态，且非对称程度越大，即地方政府和农民之间的实力悬殊越大，地方政府会越倾向于选择强硬策略，农民会越倾向于选择妥协策略。这些研究结果，不仅更好地解释了冲突现象，也为进一步治理冲突问题提供了决策方向。

第一，建立情绪监督与疏导机制，加强情绪监督与管理。针对农村征地问题，建立专门的情绪监督与管理部门。可在处于待征收或征收中的农村区域，设立专门的情绪监督与管理咨询点。通过利益相关者之间的面对面交流，及时反馈农民等参与主体的情绪状态。监督人员一旦发现某参与方具有不良情绪，应及时安排专业人员进行指导或治疗，以避免情绪极端化所导致的恶性行为。

第二，建立公平补偿机制，提高弱势群体对公平的感知度。政府应加大对补偿程序、补偿结果等公开公正的保障力度，建立和完善合理透明的补偿评估机制。前文研究表明，博弈主体的心理认知会影响其情绪的波动，那么，公平补偿机制的建立可增强农民对征地收益的信心，增加农民配合征地活动的积极性。还可在一定程度上避免弱势群体极度悲观等恶性情绪的产生，减少其策略选择的情绪化。

第三，建立利益诉求表达机制，降低信息不对称程度。通过建立利益诉求表达机制，为强弱双方提供平等对话的机会。通过不断沟通交流与反复协商，弱化认知分歧，减轻双方的信息不对称程度，降低非对称因素对征地冲突的影响。利益诉求表达机制的建立，可保障农民的知情权、表达权、监督权和受益权，减少征地冲突的发生，以实现和谐征地。

本文借助RDEU鹰鸽博弈模型研究了地方政府（或农民）的情绪因素以及非对称因素对农村征地冲突的影响，解释了情绪因素和非对称因素对征地冲突的作用机理，具有积极意义。然而，研究仍存在着不足之处，比如没有考虑多主体博弈，在未来的研究中，可以考虑引入第三方，如村集体组织、媒体等。

注释：

① 在传统的对称性鹰鸽博弈支付矩阵中，博弈双方都采取鹰策略时，各自收益为(−)/2。考虑非对称因子后，博弈双方都采取鹰策略时，各自收益变为(−)/4。可以说，对称性鹰鸽博弈模型是非对称鹰鸽博弈模型中=1/2时的一种特殊情况。非对称性鹰鸽博弈支付矩阵中其他收益值的定义与此雷同，详细情况可见参考文献[19]。

② 这里为了方便读者观察图形，选择区间(1, 10)来代替区间(1，+∞)，两者的变化趋势完全相同，以下对农民群体的分析，与此相同。

[1] 孟宏斌, 郑风田. 我国农村土地征用中的制度缺陷与主体利益冲突演化[J]. 陕西师范大学学报(哲学社会科学版), 2010, 39(4): 106−111.

[2] 吴昊, 吉林. 征地冲突中城管队长被砍死[N]. 新华每日电讯, 2014−08−02(4).

[3] 白靖利. 云南晋宁征地冲突: 见村民就打[N]. 经济参考报, 2014−10−17(5).

[4] 樊永锋. 河北白沟“11·16”开发商暴力占地案调查[N]. 中国房地产报, 2016−12−26(4).

[5] Campbell D J, Gichohi H, Mwangi A, et al. Land use conflict in Kajiado District, Kenya[J]. Land Use Policy, 2000, 17(4): 337−348.

[6] Alston L J, Libecap G D, Mueller B. Land reform policies, the sources of violent conflict, and implications for deforestation in the Brazilian Amazon[J]. Journal of Environmental Economics and Management, 2001, 39(2): 162−188.

[7] Andrew J S. Potential application of mediation to land use conflicts in small-scale mining[J]. Journal of Cleaner Production, 2003, 11(2): 117−130.

[8] Kirabo A, Byakagaba P, Buyinza M, et al. Agroforestry as a land conflict management strategy in western Uganda[J]. Environmental Research Journal, 2011, 5(2): 42−48.

[9] 祝天智, 黄汝娟. 公正视域的农村征地冲突及其治理[J]. 理论探索, 2013(4): 66−70.

[10] 霍有光, 沈红梅. 利益博弈视域下农村征地冲突与化解路 径[J]. 农村经济, 2015(9): 3−8.

[11] 柳建文, 孙梦欣. 农村征地类群体性事件的发生及其治 理——基于冲突过程和典型案例的分析[J]. 公共管理学报, 2014, 11(2): 101−114.

[12] 邹秀清, 钟骁勇, 肖泽干, 等. 征地冲突中地方政府、中央政府和农户行为的动态博弈分析[J]. 中国土地科学, 2012, 26(10): 54−60.

[13] 谭术魁, 齐睿. 中国征地冲突博弈模型的构建与分析[J]. 中国土地科学, 2010, 24(3): 25−29.

[14] 唐代中, 马卫锋. 基于演化博弈的城市拆迁补偿机制研究[J].财贸研究, 2007(6): 25−28.

[15] 熊国强, 张婷, 王海涛. 情绪影响下群体性冲突的RDEU博弈模型分析[J]. 中国管理科学, 2015, 23(9): 162−170.

[16] Quiggin J. A theory of anticipated utility[J]. Journal of Economic Behavior and Organization, 1982, 3(4): 323−343.

[17] Quiggin J. Comparative statics for rank-dependent expected utility theory[J]. Journal of Risk and Uncertainty, 1991, 4(4): 339−350.

[18] 龚日朝. 基于秩依期望效用理论的鹰鸽博弈均衡解分析[J]. 管理科学学报, 2012, 15(9): 35−45.

[19] 宋波, 黄静. 非对称性合作视角下战略联盟的稳定性分 析——基于鹰鸽博弈模型[J]. 软科学, 2013, 27(2): 28−31.

[20] Schmeidler D. Subjective probability and expected utility without additivity[J]. Econometrica, 1989, 57(3): 571−87.

[21] Diecidue E, Wakker P P. On the intuition of rank-dependent utility[J]. Journal of Risk and Uncertainty, 2001, 23(3): 281−298.

[22] Levy H. Stochastic dominance: Investment decision making under uncertainty[C]// Studies in Risk and Uncertainty,1998: 757−776.

[23] Karni E, Schmeidler D. Utility theory with uncertainty[M]. Elsevier, 1991: 1763−1873.

[24] 熊国强. 基于RDEU理论的n人非期望效用博弈模型及其应用[J]. 系统工程, 2008, 26(6): 120−123.

[25] 董海军. “作为武器的弱者身份”：农民维权抗争的底层政 治[J]. 社会, 2008, 28(4): 34−58.

[编辑: 谭晓萍]

The equilibrium analysis of RDEU Hawk-dove game model on conflict over rural land expropriation

HONG Kairong, SUN Dan

(Business School, Central South University, Changsha 410083, China)

By combining rank dependent expected utility theory model with asymmetric hawk-dove game model, the present essay constructs land expropriation compensation RDEU hawk-dove game model in order to explore the influence of the emotional factors and asymmetric factors on the behavior strategy of game participants The results show that the behavior of local governments or farmers is not only affected by the choice of the other strategies, but also influenced by the degree of emotion and asymmetry. The more optimistic, the more inclined to solve the conflict problem, the more pessimistic, the more inclined to take extreme resistance behavior, and pessimism is more likely to affect local governments’ or farmers’ behavior choices. The greater the degree of asymmetry, the more local governments tend to take tough strategies, and farmers tend to adopt a compromise strategy. The numerical simulation of MATLAB further validates this conclusion, and it provides a reference for the conflict management strategy.

conflict over rural land expropriation; RDEU theory; asymmetric hawk dove game; emotional function; Nash equilibrium

F321.1

A

1672-3104(2017)05−0095−10

2017−05 −31；

2017−07−19

国家自然科学基金面上项目“房地产征用补偿极端争议的组合性均衡评价及其实验研究”(71671187)

洪开荣(1964−)，男，四川宜宾人，中南大学商学院教授，博士生导师，主要研究方向：房地产经济理论, 博弈论及其应用；孙丹(1991−)，女，山东菏泽人，中南大学商学院硕士研究生，主要研究方向：房地产经济, 经济博弈论