巧用课本习题 促进思维发展

钱金霞

[摘 要]试题一般来源于教材，又高于教材。教材中的许多例题和习题都蕴含着重要的思想，具有典型的示范作用。教师应充分利用好课本习题，准确把握其中所承载的知识点，通过适度的重组变式、拓展延伸、开放设计，拓宽学生的视野，发展学生的思维。

[关键词]课本习题；变式；延伸；开放；思维

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2017）29-0086-01

练习是有目的、有计划、有步骤的教学活动，是学生获取知识、形成技能、发展思维的有效手段。教学中，教师不能仅将课本习题当作一种练习形式，而要巧用课本习题，对课本习题进行重组变式、拓展延伸、开放设计，培养学生的思维能力。

一、习题变式促思考

變式是指从不同角度、不同情形、不同背景对习题做调整，变式的条件或结论的形式发生变化，但其本质特征不变。

例如，五年级下册P101第14题。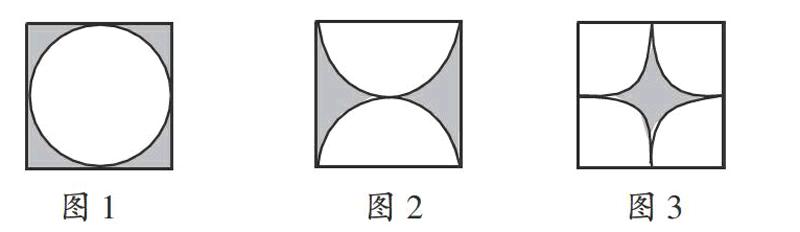

从图1～3可以看出，三幅图中的阴影部分的形状发生了变化，空白部分从一个整圆到两个半圆，再到四个四分之一的圆，但它们的本质并没有发生变化，都可以用“阴影部分的面积=正方形的面积-一个圆的面积”求得。教师还可让学生剪一剪、拼一拼，帮助学生理解其本质。图2和图3可以看成是图1的变式。

教师给出这些变式，揭示问题的本质，让学生在“变”的过程中感悟知识的真谛。

二、习题延伸引探究

延伸是以课本习题为载体，根据实际情况进行条件增减与对比等，对习题进行加工、延伸和拓展，开发习题的有效价值。

例如，四年级下册P78页第1题。

（1）延伸一——换

将第一组线段作为延伸点，把线段看成小棒，换掉最上面的小棒（小棒的长是整厘米数），使其能与其余两根小棒围成三角形，可以怎么换？要使这三根小棒围成一个三角形，必须要使任意两根小棒的长度之和大于第三根小棒。学生探索时可假设换上的小棒较短，长度大于6-4=2（厘米）；假设换上的小棒较长，长度小于6+4=10（厘米）。由此，学生探索出可换小棒长度的取值范围在2～10厘米之间，共有3、4、5、6、7、8、9厘米7种情况。

（2）延伸二——加

第一层次：“增加一根小棒，使它与原来小棒中的两根围成一个三角形，怎么加？”学生很快发现解题思路和刚才一样。

第二层次：“增加一根小棒，使它与原来的的小棒围成一个三角形，怎么加？”初看题目，只少了“的两根”三个字，但仔细分析后会发现，除了可以将增加的小棒跟其中的任意两根小棒围成一个三角形外，还可以把原来三根小棒中的两根小棒接成一根小棒，作为新三角形的一条边。由此得出新增小棒的最短长度应该大于2（4-2或6-4）厘米，最长长度应该小于12（2+4+6）厘米。

这样恰当、合理的延伸既可以丰富习题的形式，又可以拓展学生数学思维的深度和广度，帮助学生达到举一反三、触类旁通的目的。

三、习题开放活思路

教师从课本习题出发，设计开放性习题，可充分彰显学生的个性，激活和发散学生的思维，提高学生分析问题和解决问题的能力。

例如，六年级下册P75第8题：菜场运来番茄300千克，是黄瓜的■，运来黄瓜多少千克？

我们可以对这道题做如下设计。

（1）变条件

去掉“是黄瓜的■”，让学生补充“关于黄瓜和番茄间关系”的条件。比如，运来的黄瓜比番茄多50千克；番茄的重量是黄瓜的3倍；番茄比黄瓜多100千克……增加多余条件，比如，“菜场运来番茄300千克，是萝卜的■，是黄瓜的■。运来黄瓜多少千克？”

（2）去问题

让学生自己提问题。比如，运来番茄和黄瓜一共多少千克？运来黄瓜比番茄多多少千克？……

因此，教师在教学中要恰当把握课本习题所承载的知识与思想，对习题进行重组变式、拓展延伸和开放设计，培养学生学习数学的兴趣，提高学生的思维能力。

（责编 钟伟芳）endprint