培养自主探究 促进学力提高

李霞

[摘 要]数学的教学过程就是探索的过程。教师应最大限度地给学生自主探究的机会，通过创设情境，激发探究兴趣；搭建平台，提供自主探究机会，从而引导学生在新旧知识衔接处、意见分歧处自主探究，不断提高学生的自主探究能力，促进学生数学学习能力的提升。

[关键词]自主；探究；学力；提高

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2017）29-0070-02

布鲁纳曾说：“探索是数学的生命。”这句话表达了两层意思：一是数学是人们在探索的基础上创造出来的，不经历探索就不可能创造出数学知识；二是人们学习数学需要经历探索的过程，不经历探索就不能理解和掌握数学知识。基于这样的理念，小学数学课堂教学应为学生创造更多自主探究的机会，让学生在自主探究中体验、感悟、理解和掌握数学知识，并在探究过程中培养学生的思维能力、创新意识和创造能力，形成积极的情感、态度和价值观。那么，教师应如何培养学生自主探究能力呢？

一、创设情境，激发学生探究兴趣

托尔斯泰曾说：“成功的教学所需要的不是强制，而是激发学生的兴趣。”学生只有对数学感兴趣，才能激发其强烈的求知欲，才能变“要我学”为“我要学”。因此，教师在教学中要根据学生的心理特点创设既符合知识特点、又能有效调动学生学习兴趣的教学情境，以激发学生的好奇心和求知欲，吸引学生的注意力，使学生积极主动地投入到数学探究之中，从而提高课堂学习效率。

例如，在教学苏教版教材第六册中的“年、月、日”时，教师可以创设贴合学生实际的情境展开教学。

师：生1，今年你几岁了？过了几次生日？

生1：我今年10周岁，过了10次生日。

师：其他同学呢？

……

师：有一位小朋友，今年12周岁，但是他只过了3次生日，你们知道这是为什么吗？

生2：一定是他忘记过生日了。

师：不是他忘记过生日，而是他在有的年份里没有生日，没办法过生日。

生3：这是为什么呢？

此时，学生的积极性一下子就被调动了起来，在强烈的好奇心和求知欲的驱使下，学生迅速投入到了观察年历表、研究年历表的活动中。

二、搭建平台，提供自主探究机会

完全依靠教师的讲解，然后让学生死记硬背或进行机械式的重复练习的传统教学模式，并不能提高学生的学习能力。教师要帮助学生在“理解”上做文章，让学生动手实践、自主探究、合作交流，经历知识的发生、发展、变化的动态形成过程，只有经历这样的过程，学生才能学到活的知识。因此，在课堂教学中，教师不能扮演“传教士”的角色，要多为学生搭建自主探究的平台，多提供探究的机会，让学生在探究中知道知识的来龙去脉、明白其中的道理，形成对数学知识的深刻感受。

1.在新舊知识衔接处让学生自主探究

如，在教学“平行四边形的面积”时，教师可以分四步引导学生进行探究。

（1）探究面积与什么有关系。

师：（出示等底不等高的两个平行四边形，如图1）比较这两个平行四边形，哪一个的面积大？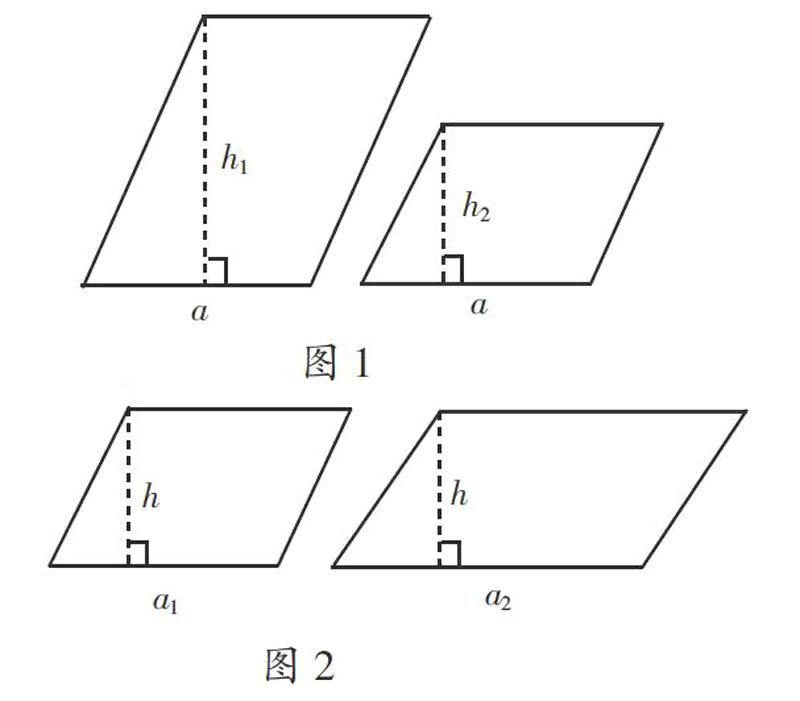

生1：高长的那个平行四边形的面积大。

师：（出示等高不等底的两个平行四边形，如图2）现在又是哪一个的面积大？

生2：底长的那个平行四边形的面积大。

师：通过上面的比较，你们发现平行四边形的面积与什么有关系？

生3：与平行四边形的底和高有关系。

（2）探究转化的方向。

师：平行四边形的面积与它的底和高有什么关系？你打算怎样研究呢？

生1：可以把这个平行四边形转化成长方形来研究。

师：为什么要转化成长方形，而不转化成三角形来研究呢？

生1：因为我们已经学过了长方形的面积计算，所以将平行四边形转化成长方形后就可以算出它的面积。如果转化成三角形，我们还不会计算三角形的面积，就不能推导出平行四边形的面积。

（3）探究转化的方法。

师：怎样把平行四边形转化成长方形或正方形呢？

（先引导学生独立思考并操作，再让同桌的学生交流讨论，最后全班汇报）

生1：将平行四边形转化成长方形的方法——先画出平行四边形的高，再沿高将平行四边形剪成两部分，最后平移其中一部分拼成一个长方形。（如图3）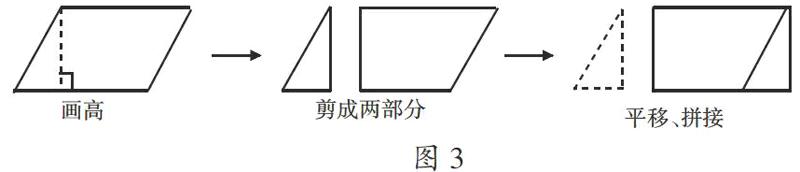

（4）探究面积公式。

师：转化后的长方形与原来的平行四边形有什么关系？

（让学生对照剪拼的图形进行探究）

生1：转化后的长方形的长与原来的平行四边形的底相等，长方形的宽与原来的平行四边形的高相等，转化后的长方形的面积与原来的平行四边形的面积相等。从而推导出平行四边形的面积=底×高。

在这样的探究活动中，学生不但对平行四边形的面积计算公式有了深刻的认识和充分的理解，而且有效地培养了学生的观察能力、操作能力、思维能力及推理能力。

2.在意见分歧处让学生自主探究

由于不同的学生有不同的生活经验、基础知识和思维方式，所以即使是同一个班级的学生，对某个问题的认识也常常会存在分歧，这就需要教师加以引导、启发和点拨，在学生独立思考并形成初步认识的基础上组织学生进行辩论。学生在辩论中互相启发、取长补短，实现群体思维资源的共享，从而使学生深刻理解并牢固掌握数学知识。endprint

如，教师出示“租车出游”例题：“学校组织学生外出秋游，一共有420个学生参加。每辆大客车限坐50人，租金250元；每辆小客车限坐30人，租金160元。怎样租车最划算？”学生通过研究得出两种租车方案：方案一是由于大客车比小客车的单人票价便宜，所以全租大客车420÷50≈9（辆）；方案二是租小客车没有座位浪费，所以全租小客车420÷30=14（辆）。在不计算每一种方案各需要花多少钱的前提下，让学生判断哪种租车方案划算。学生都认为自己的方案划算，于是教师放手让学生辩论，看能否想办法说服对方。

生1：如果租大客车，平均每人要花250÷50=5（元）；如果租小客车，平均每人要花160÷30>5（元）。因为大客车的单人票价更便宜，所以应全租大客车划算。

生2：不对！虽然大客车的单人票价更便宜，但是一共要租420÷50≈9（辆）大客车，就浪费了50×9-420=30（个）座位，因此并不划算。

生3：我算过了，如果全租大客車，一共要花250×9=2250（元）；如果全租小客车，一共要花160×14=2240（元）。因此，全租小客车划算。

生4：我认为全租小客车还不是最划算的，因为租小客车虽然没有浪费坐位，但是租小客车每人花的钱要比租大客车的贵。

生5：我觉得解决这个问题，既要考虑不浪费座位，又要考虑租一些座位相对便宜的大客车。

生6：我知道怎么思考了，就是大客车和小客车都租，并把坐两种车的人数凑成420人，因为50×3+30×9=420（人），所以租3辆大客车和9辆小客车最划算，一共要花250×3+160×9=2190（元）。

生7：这还不是最划算的，大客车还可以再多租一些。因为50×6+30×4=420（人），所以租6辆大客车和4辆小客车最划算，一共要花250×6+160×4=2140（元）。

师：通过探究，你有什么话想对全班同学说？

生8：解决这道题目时，想做到最划算就要先从两个方面考虑——一是尽量多租便宜的车，二是不要浪费座位。然后列出适合的租车方案，再算一算每种租车方案的租金是多少，最后按租金判断怎样租车最划算。

事实胜于雄辩，学生在思考中辩论，在辩论中再思考，学生之间相互吸收他人有价值的思维成果，不断完善和充实自己，最终明白了租车问题中的学问，掌握了租车的思维方法。在这个教学过程中，学生解决的不仅仅是一个租车问题，而是解决了类似于租车问题的思考方法，不但拓展了学生解决问题的思路，而且有效地训练和发展了学生的思维能力。

总之，要实现新课程提出的数学教育目标，教师必须要转变观念，变数学教学为数学教育，同时，教师还必须改变传统的教学方式，变讲授式教学为探究式教育模式，课堂上多为学生提供自主探究的机会，让学生在情境中发现问题、提出问题、探究问题，在解决问题的过程中理解和掌握数学知识，培养学生的创新意识和创造能力，从而不断促进学生数学学习能力的提高。

（责编 李琪琦）endprint