透析核心 探究本质

唐妍

[摘 要]小数与整数、分数有着紧密的联系，教师在教学 “小数的意义”时，应紧密联系生活实例，帮助学生理解小数的本质内涵，剖析小数与分数、整数之间的关系，通过变式应用等方式建立小数与十进制之间的关系，最终使学生深刻理解小数的意义，体会小数的重要作用。

[关键词]小数意义；十进制；分数；整数

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2017）29-0048-01

小数的意义是学生掌握小数知识必不可少的部分。通过对“小数的意义”进行教学，可使学生深入理解小数的意义和本质，从而为小数运算的学习奠定基础。下面以“小数的意义”的教学为例谈谈如何引领学生探究数的本质。

一、重温旧知，引入新课

师（出示图1）：这里的小数具体表示什么？

生1：0.4元表示4角钱，78.78元表示78元7角8分钱，0.6米表示6分米。

师：为什么说6分米就是0.6米呢？

生1：因為米和分米的进率是十，1米就等于10分米，所以说6分米就是0.6米。

生2：6分米就是将1米平均地分为10份，那么其中的6份就是6/10米，所以说是0.6米。

师：总的来说，6分米就是0.6米。

师（出示数字“0.1”）：这里的0.1具体表示什么呢？

生3：可以表示0.1元、0.1分米、0.1公里。

……

上述教学案例中，通过设问“为什么说6分米就是0.6米”，自然引出小数与十进制之间的关系，然后通过提问“0.1具体表示什么”引发学生的思考。这样的教学设计体现了“认知是课堂教学的出发点”这一理念。

二、迁移学习，探究实质

师（出示一个正方形）：如果用整数1表示这个正方形，大家可以用绘图的方式表示出0.1吗？

生1：将正方形平均分为10份，每一份就是1/10，也就是0.1。（如图2）

师：很好。也就是说0.1可以表示1/10，这也是小数0.1的真实意义。

师：如何用一句话来概括？

生3：零点几表示十分之几。

师：在零点几中，0.1是最小的，也就是十分之一，它也是零点几的计数单位。我们把平均分成的10份全部涂色，则涂色的部分就是10个0.1，那么10个0.1也就是1。

上述教学案例中，教师以正方形为学习载体对学生进行思维拓展训练，通过平分正方形形象地展示小数形成的过程，使学生深刻理解小数的意义。同时，使用较为直观的图示法，将小数与十进制联系在一起，使学生能够结合分数初步理解小数的本质。

三、变式练习，深化理解

师（出示图3）：请大家用小数来表示这些图形的涂色部分。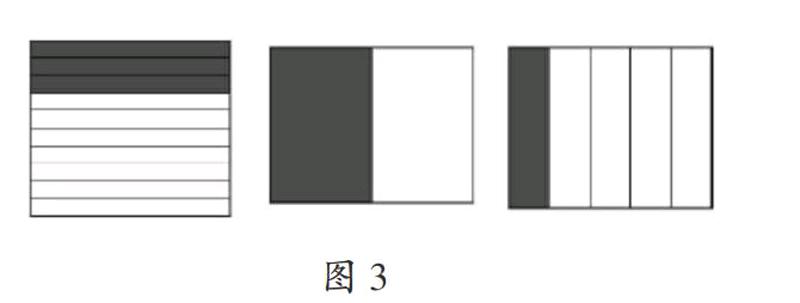

生4：第一幅图表示0.3，第二幅图表示0.5。

师：为什么第二幅图是0.5呢？

生4：因为只涂了一半，所以就是0.5。

生5：不是0.5，应该是0.1，因为只涂了1份。

生6：是0.5，把这幅图想象成平均分成了10份，那么涂色的部分就是5份，所以是0.5。

师：很好，那第三幅图表示什么呢？

生6：表示0.2，可以想象成把每一份再平均分成两份，这样就平均分成了10份，涂色的有2份，所以是0.2。

师：后面两幅图虽然没有平均分为10份，但依然可以想象成平均分为10份。

上述教学案例中，通过数形结合的方式引导学生感知小数的组成，学生就能在自主探究的过程中理解小数的本质内涵，掌握小数与计数单位之间的内在联系。

综上可知，教材是教学的主要依据，教师教学时应基于对教材的理解，做到从教材出发，适度结合生活实际，从而帮助学生构建知识体系，使学生形成更为有效的学习动机，实现有效学习和全面发展。

（责编 黄春香）endprint