三浮陀螺磁悬浮干扰力矩机理分析

王 雪，邓忠武，马 宁

（1.北京航天控制仪器研究所，北京 100854；2.陕西航天时代导航设备有限公司，宝鸡 721000）

三浮陀螺磁悬浮干扰力矩机理分析

王 雪1，邓忠武1，马 宁2

（1.北京航天控制仪器研究所，北京 100854；2.陕西航天时代导航设备有限公司，宝鸡 721000）

在三浮陀螺磁悬浮的干扰力矩研究方面，详细分析了磁悬浮干扰力矩的产生机理，对机加和装配误差、磁性材料的不理想、调试过程等可能造成的磁悬浮干扰力矩进行了定性分析和定量计算，推导出干扰力矩的表达式，并通过组合加工的方法对磁悬浮干扰力矩的力臂加以控制。目前的加工水平可以达到：径向磁悬浮干扰力矩1×10-8N·m，对应的陀螺漂移8.4×10-2(°)/h，随机分量4.2×10-6(°)/h；轴向磁悬浮干扰力矩2×10-10N·m，对应的陀螺漂移1.7×10-3(°)/h，随机分量为 8.4×10-8(°)/h。

三浮陀螺；磁悬浮；干扰力矩；机理分析

三浮陀螺仪是在单自由度液浮积分陀螺基础上研制的高精度惯性器件。“三浮”是指其陀螺马达采用动压气体支承，陀螺输出轴采用液浮+磁悬浮的支承方式。磁悬浮一方面可以消除剩余的重浮力差，使浮子组件处于悬浮状态；另一方面可以使浮子精确定中，有效地提高了陀螺的精度和稳定性[1-2]。

作为惯性导航系统的核心部件，陀螺仪的精度与导弹的命中精度密切相关，通常用陀螺的漂移来对其进行表征。陀螺漂移由陀螺输出轴上存在的各种干扰力矩引起[3-7]。为降低输出轴轴承的干扰力矩，三浮陀螺采用磁悬浮支承确保了浮子轴尖与宝石轴承不接触，完全消除了机械接触摩擦引起的干扰力矩，但是，它给陀螺带来了新的误差源——磁悬浮干扰力矩。磁悬浮干扰力矩对仪表输出的常值漂移和随机漂移都会产生影响[8-11]。磁悬浮干扰力矩与磁悬浮元件的机械加工精度和工艺要求、软磁材料的磁性能、浮子定中位置的选取等要素密切相关。

1 机加装配的影响

磁悬浮元件（特别是磁悬浮转子）的机加和装配的精度是造成磁拉力产生干扰力矩的主要原因。由于机加和装配过程中的不理想是永远无法完全消除的，为了提高陀螺的使用精度只能对磁悬浮干扰力矩进行抑制。进行抑制的前提是要对可能造成干扰力矩的各种因素的作用机理进行理论分析和估算。

从干扰力矩的作用形式和产生机理来看，磁悬浮干扰力矩主要分为由轴向、径向磁悬浮，它们有很大区别，下面分别进行分析和计算。

1.1 径向磁悬浮干扰力矩的分析

按照误差的来源，可将径向磁悬浮的干扰力矩分为圆度误差干扰力矩和安装误差干扰力矩两部分。1）圆度误差干扰力矩

圆度误差干扰力矩是指由于转子表面加工的几何误差所引起的干扰力矩，在所有类型的磁悬浮干扰力矩中占主要成分。如图1所示，在每个径向磁悬浮转子上有四个独立磁场，每对磁极间磁拉力的大小随浮子的位置而变化。理想情况下，径向磁悬浮转子外圆如图2中虚线所示，受转子外圆圆度误差的影响，实际转子表面情况如实线所示。磁悬浮转子所受到的磁拉力方向始终垂直于转子表面，如果磁拉力的作用线不通过整个转子的中心，就将产生干扰力矩。

图1 径向磁路示意图Fig.1 Radial magnetic circuit diagram

图2 径向转子表面示意图Fig.2 Radial rotor surface diagram

为分析简便，假设转子沿轴向方向是均匀的，这样就可以通过建立二维平面视图来分析转子圆度误差所产生的径向干扰力矩。如图3所示，将转子表面划分为和理想表面存在不同夹角的微小折线。首先计算转子的某一小段折线AB和转子母线构成/的微小面积上的磁拉力dF产生的干扰力矩。

设AB所对应的圆心角为dθ，由于dθ很小，故：

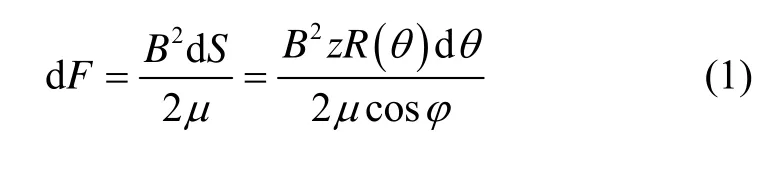
图3 径向转子圆度误差干扰力矩分析示意图Fig.3 Disturbance moment analysis schematic diagram of radial rotor roundness

式中，

其中：z为径向转子长度；B为转子表面磁感应强度，它是角度θ的函数；为沿转子圆周方向所取微元的起点和终点所对应的半径差。在每一个独立磁场覆盖下的圆弧段内，B可以认为是常数，即：

由径向转子的圆度误差造成的第i对径向磁极的干扰力矩：

在2π范围内求其代数和，得到圆度误差造成的整个径向转子的干扰力矩：

式中：Ri、Ri-1分别为第i对径向磁极沿转子圆周方向的起点和终点所对应的半径差。

由式(7)可以看出，磁悬浮的圆度误差干扰力矩和B的平方成正比。虽然在每一个独立磁场覆盖下的圆弧段内，B可以认为是常数，但磁悬浮在工作过程中，由于浮子位置的不确定性使得径向磁悬浮元件之间工作气隙的长度在很小范围内是随机的，而B随定、转子相对位置的变化而变化，因此，磁悬浮的圆度误差干扰力矩在磁悬浮工作过程中存在一定的随机分量，随机分量的大小与式(7)计算的常值分量成正比，与磁悬浮工作气隙长度变化量的平方成正比。

由式(7)得：

设磁悬浮工作气隙长度为0.08 mm，变化量为5μm，参考MjO的推导过程，其随机分量为

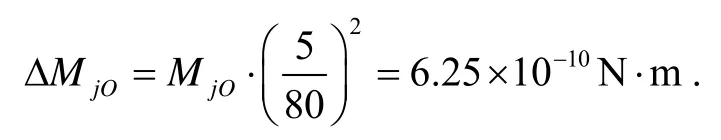
2） 安装误差干扰力矩

在没有安装误差的理想情况下，径向磁悬浮定子轴线与陀螺输出轴平行，转子轴线与陀螺输出轴和浮子轴重合。此时，每对径向磁极产生的磁拉力的方向都与浮子轴共面且垂直，不会产生绕浮子轴的干扰力矩。实际装配情况如图4所示。由于安装误差的影响，使得径向定、转子轴线与浮子轴都存在夹角，转子轴向与浮子轴OF之间还有一定的偏心。

图4 径向转子实际安装示意图Fig.4 Radial rotor actual installation diagram

图4中，OF为浮子轴，OZ为径向转子轴线，OD为径向定子轴线，ψ、Φ分别为径向转子轴线与浮子轴和径向定子轴线之间的夹角，λ为径向转子中心与浮子轴之间的偏心距。ψ、Φ的存在改变了径向磁悬浮定、转子元件之间的工作间隙沿转子轴线方向的均匀性，使得磁极间的磁拉力Fj、Fj′的方向与实际转子的表面垂直而不垂直于浮子轴。磁拉力可以分别分解成平行于浮子轴方向的Fjj、Fjj′和垂直于浮子轴方向的力Fnj、Fnj′，这两对力产生的力矩均垂直于浮子轴方向。因此，由安装误差造成的径向转子轴线与浮子轴的夹角和径向转子轴线与径向定子轴线之间的夹角不会产生绕陀螺浮子轴方向的干扰力矩。

图5 浮子受力图Fig.5 Float free-body diagram

下面计算图 5中径向磁悬浮转子相对浮子轴的偏心δ引起的绕陀螺浮子轴的干扰力矩。将δ分解成沿陀螺的自转轴SA的分量δIA和沿输入轴IA的分量为由图5得到由于偏心δ所产生的绕浮子轴的干扰力矩：

磁拉力：

则：

由式(10)可以看出，MjA和转子表面磁感应强度B的平方成正比。与圆度误差干扰力矩一样，MjA在磁悬浮工作过程中也存在一定的随机分量，它与式(10)计算的常值分量成正比，与磁悬浮工作气隙长度变化量的平方成正比。

一般情况下，如不采取特殊措施，径向磁悬浮转子与陀螺框架的同轴度为 5～10μm，假设其沿SA、IA方向的分量径向磁悬浮的磁拉力1F、F4均为0.05 N，F2、F3均为零，则径向磁悬浮因偏心产生的干扰力矩为：

磁悬浮工作气隙长度为0.08 mm，变化量为5μm，则随机分量为：陀螺电机角动量为它对陀螺造成的漂移随机分量为

1.2 轴向磁悬浮干扰力矩的分析

理想情况下轴向磁悬浮定、转子的对称轴都与陀螺浮子轴重合，定、转子的表面互相平行并与浮子轴垂直。这时，磁悬浮定、转子之间的气隙均匀且垂直于浮子轴。系统工作时磁悬浮定子线圈通电，定、转子和气隙形成电磁通路，气隙中的磁力线互相平行且垂直于定、转子表面，定、转子之间的磁拉力方向与磁力线方向一致且平行于浮子轴，轴向磁拉力不会产生绕陀螺浮子轴方向的干扰力矩。机加和装配精度的影响使得轴向磁悬浮的实际工作情况如图6所示。

图6 轴向元件实际安装示意图Fig.6 Actual installation diagram of axial elements

磁悬浮定、转子元件的对称轴O1D、O2Z与陀螺的浮子轴都有一定的夹角α、β和偏心δ1、δ2，定、转子安装平行度和转子表面加工平面度的影响使得定转子之间的气隙不均匀，造成了轴向磁悬浮转子所受到的磁拉力并不完全平行于浮子轴的方向。

图7 轴向转子表面微元示意图Fig.7 Tiny unit diagram of axial rotor surface

在图 7中，设σ为理想平面（σ与浮子轴垂直），图中所示圆环为实际的轴向磁悬浮转子在理想平面上的投影。在平面σ上沿着转子表面的圆周方向任取一段微小圆弧AB，它对应的圆弧角为dθ，并将dθ对应的转子表面积记为dS，如图中阴影部分所示。理想情况下，微元dS所受的磁拉力方向应垂直于平面σ。然而，由于各种不理想情况的存在使得实际转子与理想平面不重合，因此，理想平面上的微元dS所对应的实际转子所受到的磁拉力并不垂直于平面σ，而垂直于其实际转子表面。假设实际转子的受力为图8中所示dFz的方向。

将转子所受到的电磁拉力dFz沿理想转子所在平面σ分解为切向力dFj和径向力dFn。只有切向力产生绕浮子轴方向干扰力矩，若按干扰力矩最大时的条件计算时，

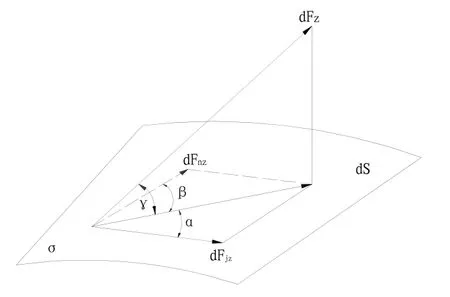
图8 轴向转子微元受力分析Fig.8 Stress analysis of axial rotor tiny unit

磁悬浮轴向的干扰力矩与轴向磁悬浮元件自身的平面度，磁悬浮定转子安装的平行度有关。当元件自身的平面度很好，磁悬浮定转子安装的平行度比较理想时，定转子之间的磁场可视为均匀磁场，轴向磁悬浮的干扰力矩可以得到抑制。

轴向磁悬浮的磁拉力方向沿着输出轴方向，当陀螺沿输出轴方向有过载时，剩余重浮力差将由轴向磁悬浮来承载，而轴向磁悬浮干扰力矩的存在是产生三浮陀螺项漂移的因素之一。设轴向磁拉力为0.05N，轴向元件的定转子平行度为5μm，轴向转子平面度为1μm时，根据行位误差的传递机理，轴向磁悬浮作用力的等效力臂约为轴向磁悬浮的最大径向分力约为 0.5mg，此时，轴向磁悬浮造成的沿输出轴方向的干扰力矩约为对应的陀螺漂移ωd≈随机分量可见，轴向磁悬浮干扰力矩远小于径向磁悬浮干扰力矩。

2 磁性材料的影响

2.1 涡流损耗

按照材料划分，三浮陀螺磁悬浮元件可分为镍铁叠片和铁氧体。从作用机理上来看，磁性材料引入干扰力矩的主要途径是磁性材料的不均匀性和各向异性引起磁通密度分布的畸变，而这类不均匀性和各向异性又引起了涡流分布和磁滞损耗的不对称。在满足一定条件下可以近似认为，在镍铁叠片元件中铁芯损耗是涡流损耗，在铁氧体元件中铁芯损耗是磁滞损耗。

涡流损耗主要从磁悬浮元件的功耗方面考虑。小的涡流损耗的热效应本身不会对仪表有严重的影响，因为与温控系统产生的热量相比铁芯损耗的热效应要小得多，但随着时间和环境条件的变化，涡流分布的不对称造成的机械不稳定可能影响到元件的几何形状，结合第1节的分析可知几何形状的不对称会带来干扰力矩。

涡流效应抑制的是磁悬浮元件的设计内容，从对仪表精度的影响考虑，还是要对涡流损耗加以严格控制的。通常可以采用两种方法来降低材料的涡流损耗：一是采用热轧或冷轧的方法将铁磁材料轧成薄片叠起来使用以降低材料的厚度，二是在金属磁性材料加入合金元素以提高材料的电阻率。

2.2 磁滞损耗

与涡流损耗类似，磁滞损耗也会提高系统的平均功耗进而降低系统的刚度。磁滞损耗对磁悬浮性能的影响可以通过品质因数表现出来。降低磁滞损耗的最好办法是减小材料的矫顽力，矫顽力的降低会使磁滞回线变窄以减小它所围成的面积，而面积减小的实质是能量损耗的减小。

在惯性仪表中抑制磁滞干扰力矩的主要途径是从磁性材料的选择出发，尽量选择磁滞角小的材料。三浮陀螺用镍铁叠片铁芯代替铁氧体磁芯，在降低磁滞的同时减小了材料的加工难度。

3 调试过程的影响

三浮陀螺调试过程中的湿对中过程确定了浮子的定中位置，定中位置决定了磁悬浮的磁拉力的分布，磁拉力与力臂共同作用形成了力矩，因此，不同定中位置对应着不同的干扰力矩。

定中位置有两个选择，一个是磁悬浮定子的几何中心，另一个是宝石轴承的中心。原则上，一般把定中位置选在宝石轴承的中心，此时轴尖与宝石轴承之间相对距离最远，系统的可靠性和安全性最高，但这时由于磁悬浮元件的各极加力不完全通过浮子轴，就会带来磁悬浮干扰力矩。

为了提高仪表性能，除了应根据实际情况选取合适的定中位置外，最根本的还是要对磁悬浮元件的加工和仪表的装配过程加以严格的要求和控制，尽量保证磁悬浮力中心和输出轴结构中心的重合度。

4 结 论

从磁悬浮系统自身出发，深入地讨论了机加和装配精度、磁性材料以及调试过程对磁悬浮干扰力矩和仪表精度的影响。从磁悬浮干扰力矩产生机理可以看出：磁悬浮元件的加工精度和装配精度是产生磁悬浮干扰力矩的主要的原因，它决定了磁悬浮作用力相对于浮子轴的力臂。磁性材料和调试过程也对磁悬浮干扰力矩有所影响。

为了降低磁悬浮系统的干扰力矩，可以从以下三方面着手：设计上，选择涡流损耗和磁滞损耗小的材料；机加上，采用组合加工的办法提高磁悬浮元件相应部位的加工精度，其中包括提高径向磁悬浮转子圆度、径向磁悬浮转子和陀螺框架的同轴度，轴向磁悬浮转子的平面度，轴向磁悬浮定、转子平行度；装配和调试上，采用精细装调来进一步抑制磁悬浮干扰力矩。

（References）：

[1]王巍.惯性技术研究现状及发展趋势[J].自动化学报,2013, 39(6): 723-729.Wang W.Status and development trend of inertial technology[J].Acta Automatica Sinica, 2013, 39(6): 723-729.

[2]王立旭, 常晓华, 杨云翔.国外战略导弹制导系统惯性器件发展趋势分析[J].航天控制, 2016, 34(2): 95-98.Wang L X, Chang X H, Yang Y X.Development tendency analysis of the inertia device in foreign strategic missile[J].Aerospace Control, 2016, 34(2): 95-98.

[3]Su B K, Li Y B, Liu Y, et al.Improved gyroscopic drift test scheme by low-angle servo method[J].Journal of Chinese Inertial Technology, 2010, 18(6): 766-770.

[4]Wang S M, Meng N.A new multi-position calibration method for gyroscope’s drift coefficients on centrifuge[J].Aerospace Science and Technology, 2017, 68: 104-108.

[5]Shen Y, Hasanyan D, Gao J Q, et al.A magnetic signature study using magnetoelectics laminate sensors[J].Smart Material and Structures, 2013, 22: 095007(1-7).

[6]杨孟兴, 吴辽, 王卿, 等.基于位置信号的三浮陀螺仪有源磁悬浮干扰力矩补偿方法[J].中国惯性技术学报,2015, 23(6): 812-817.Yang M X, Wu L, Wang Q, et al.Disturbance-torque compensation for active magnetic bearing of three-floated gyroscope based on position signal[J].Journal of Chinese Inertial Technology, 2015, 23(6): 812-817.

[7]于佳福, 徐静.三浮陀螺仪磁悬浮轴承干扰力矩测控技术[J].导航与控制, 2014, 13(1): 15-28.Yu J F, Xu J.The technology for measuring and controlling the disturbance torque for magnetic bearing of three-floated gyroscope[J].Navigation and Control, 2014,13(1): 15-28.

[8]Wang X, Zhu Z G, Deng Z W.Optimal design of magnetic suspension system in three-floated gyroscope[C]//Proc of 2010 international symposium on inertial technology and navigation.Nanjing, China, 2010: 288-293.

[9]郝晨, 张卫均, 姜大千, 赵斌.提高三浮加表磁悬浮工作精度的工艺研究[C]//中国惯性技术学会第七届学术年会论文集.武汉, 中国, 2015: 216-221.Hao C, Zhang W J, Jiang D Q, et al.Study on technology of improving the working precision of PIGA[C]//Proc.of 2015 International Symposium on Inertial Technology and Navigation.Wuhan, China, 2015: 216-221.

[10]Hutterer M, Kalteis G, Schrodl M.Redundant unbalance compensation of an active magnetic bearing system[J].Mechanical System and signal Processing, 2017, 94: 267-278.

[11]Zheng S, Han B, Wang Y, et al.Optimization of damping compensation for a flexible rotor system with active magnetic bearing considering gyroscopic effect[J].IEEE/ASME Transactions on Mechatronics, 2015, 20(3): 1130-1137.

Mechanism analysis on magnetic suspension bearing disturbance moment in three-floated gyroscope

WANG Xue1, DENG Zhong-wu1, MA Ning2
(1.Beijing Aerospace Control Instrument Research Institute, Beijing 100854, China;2.Shaanxi Space Time Navigation Equipment Co., Ltd, Baoji 721000, China)

On the research of the disturbance moment of magnetic suspension bearings in three-floated gyroscope, the author analyzed the mechanism and carried on the qualitative analysis and quantitative calculation on the disturbance moment that might be caused by the error in the process of machining, and the un-ideal of the magnetic material, assemblage and debugging.The expression is deduced, and the force arm is restricted by the combining processing.Currently, it can be achieved that: the radial disturbance moment is 1×10-8N·m, the gyro drift is 8.4×10-2(°)/h, and the random component is 4.2×10-6(°)/h; the axial disturbance moment is 2×10-10N·m, the gyro drift is 1.7×10-3(°)/h, and the random component is 8.4×10-8(°)/h.

three-floated gyroscope; magnetic suspension; disturbance moment; mechanism analyzing

U666.1

A

1005-6734(2017)05-0681-05

10.13695/j.cnki.12-1222/o3.2017.05.021

2017-06-27；

2017-09-25

总装预研项目（51309050101）

王雪（1981—），女，高工，从事三浮陀螺仪表研究。E-mail: woshimao9216@sina.com

联 系 人：邓忠武（1971—），男，研究员。E-mail: dzweng@126.com