基于伪地球坐标系的捷联惯导全球动基座初始对准算法

刘 猛，高延滨，李光春，孟庆文，马文霞

（哈尔滨工程大学 自动化学院，哈尔滨 150001）

基于伪地球坐标系的捷联惯导全球动基座初始对准算法

刘 猛，高延滨，李光春，孟庆文，马文霞

（哈尔滨工程大学 自动化学院，哈尔滨 150001）

由捷联惯导系统建模原因造成的导航误差随纬度升高会被急剧放大，是实现惯导系统全球初始对准所面临的主要问题之一，且现有多种编排方案共存的全球初始对准算法也不利于初始对准算法在全球范围内统一。另一方面，极地地区越来越小的地球自转水平分量，使得极点及其附近的静态自对准是无法实现的，且动基座初始对准也有利于提高导航系统的快速反应能力。基于此，提出了采用伪地球坐标系惯导编排来实现惯导系统的全球动基座初始对准，消除由惯导建模造成对全球初始对准性能的影响，并期望探索一种统一导航编排的全球初始对准算法。最后通过仿真证明了该算法的可行性。

极区对准；全球初始对准；捷联惯导系统；动基座初始对准

惯导系统建模原因造成导航误差随纬度升高被急剧放大，是捷联惯导系统全球初始对准所面临的主要问题之一[1]。在传统的指北方位系统模型中，惯性导航的东向线性运动误差对方位误差的影响是随纬度成正切函数增加的[2]，因此在极区的一个很小的东向线性运动误差干扰就可能引起非常大的方位误差波动。另外由于方位失准角的不完全可观测[3]，线性运动误差和方位误差之间耦合使得方位对准对系统误差特别敏感，从而非常容易引起初始对准系统的发散。因此必须选择一种合适的力学编排来解决惯导的全球初始对准问题。对于中低纬度的初始对准，通常采用传统的指北方位力学编排，而且国内外已经进行了大量的研究，其理论已相当完善[4]。然而对于高纬度和极地地区初始对准的研究则相对还比较薄弱。文献[5]提出了在横向地球坐标系力学编排下的传递对准方法来完成极区对准，从而得到横向地球坐标系下的捷联矩阵；文献[1]和[6]提出了基于雷达辅助的格网坐标系初始对准算法，从而求得格网坐标系下的捷联矩阵；文献[7]则采用无迹卡尔曼来解决在格网坐标系下的大失准角的传递对准问题，得到格网坐标系下的捷联矩阵。然而无论是指北方位编排，还是横向惯导编排，亦或是格网惯导编排，它们单独都不具备实现全球初始对准的能力[8]。尽管在格网坐标系或横向地球坐标系下进行初始对准可以解决高纬度和极区初始对准的惯导建模的问题，但是多种编排方案共存的全球初始对准算法不利于实际工程的实施。因此在此期望探索一种统一导航编排的全球初始对准方案，消除由惯导系统建模造成对全球初始对准性能的影响。

为了消除惯导系统建模对初始对准性能的影响，文献[9]提出采用伪地球坐标系惯导编排的捷联惯导初始对准算法，消除了导航坐标系旋转角速度误差对方位对准的影响。由于伪地球坐标系是根据载体的初始位置进行构建的，它不仅可以用于常规纬度的初始对准，也可以用于极区初始对准，而且其在常规纬度的初始对准中也具有良好的对准结果，并可以改善惯导系统初始对准的性能，然而文献[9]仅研究了惯导系统的静基座初始对准。其次，随着纬度的升高，地球自转的水平分量会越来越小，最终为零，从而使方位失准角的可观测性变得越来越小，故极点以及极点附近的静态初始对准将是无法实现的。为了实现极点及其附近的初始对准，则必须利用外部信息辅助的动基座初始对准来进行完成[10]。另一方面，随着当今军事科学技术的发展及国际政治经济军事形势的多变性，各军事强国对舰艇和战机的快速反应能力和全球作战能力都提出了更高的要求，动基座初始对准则可以满足武器装备的高机动性和紧急启动任务的特点[11-12]。因此研究惯导系统全球范围内动基座初始对准是十分有必要的。

针对上述问题，本文提出了采用伪地球坐标系惯导力学编排来实现捷联惯导全球动基座初始对准，对其过程进行了深入研究，并期望对全球动基座初始对准算法进行统一。最后通过仿真验证该算法的可行性。

1 伪地球坐标系定义与力学编排

伪地球坐标系用Oxp yp zp表示，是根据载体的初始位置来进行构建的，可以认为是一种广义的横向地球坐标系。在伪地球坐标系中，伪赤道同当地位置所在的子午圈是重合的，其坐标原点仍在地球中心，Np为伪北极点，Oxp轴与原Oze重合，Oyp轴是指向载体初始位置在赤道平面的投影点，Ozp在赤道平面内垂直于Oyp轴，如图1所示，其具体的定义详见文献[9]。

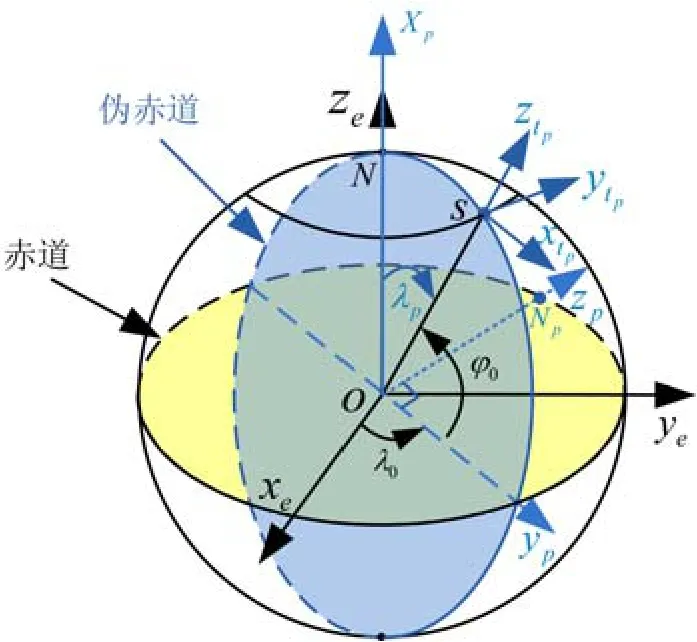
图1 伪地球坐标系定义Fig.1 Definition of pseudo-Earth frame

假设载体的初始位置的经纬度为0λ和0φ，则从地球坐标系到伪地球坐标系的旋转矩阵为

其中：

对于伪地球坐标系统，其定义同横向地球坐标系和传统的地球坐标系是相似的。伪地理坐标系(即伪东-北-天)的定义也是同横向地理坐标系和传统的当地地理坐标系是相似的[9]，如图1所示。在伪地球坐标系中，载体的位置用伪经纬度和伪高度表示，即pλ、pφ和hp，则伪初始位置可以表示为

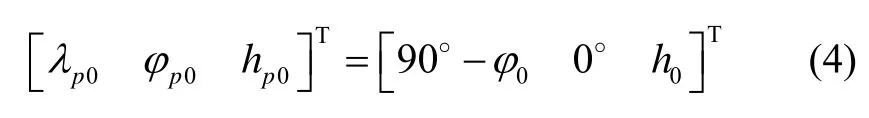
伪惯导力学编排同横向惯导编排和传统指北方位编排也是相似的。在伪惯导指北力学编排中，仅由地球自转引起的伪地理坐标系旋转角速度和传统指北方位系统是不一致，因此基于伪地球坐标系的伪导航方程可以给出[9]：

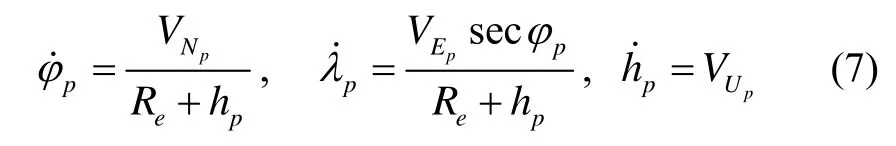
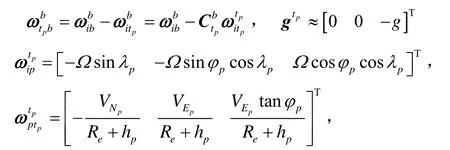
2 基于伪地球坐标系的全球动基座初始对准方案

基于伪惯导编排的捷联惯导初始对准算法对静基座初始对准具有优良的性能[9]，且该算法不受载体初始位置的限制，可以应用于全球初始对准，因此它也期望被应用在动基座初始对准中。另一方面，目前常用的惯性导航全球导航方案中，通常采用指北方位系统+格网惯导系统/横向惯导系统的方法来实现全球导航[13]，故在极区可以利用已有的转换程序，实现当地地理坐标系下捷联矩阵和格网或横向地球坐标系下的捷联矩阵之间的转换将是最方便的。另外，目前惯性导航系统在中低纬度仍采用指北方位系统，因此在全球范围内的惯导系统初始对准结束时，传统当地地理坐标系下的捷联矩阵是期望被得到的。当基于伪惯导力学编排的初始对准算法应用于动基座初始对准时，当地地理坐标系下的捷联矩阵可以根据伪捷联矩阵得到：

其中：

根据导航系统解算出的载体伪位置，式(11)是容易得到的，进而我们利用伪位置和传统当地位置之间的关系，式(10)也是容易求得的。因此根据式(8)，惯导系统当地地理坐标系的捷联矩阵可以实时给出。下面我们将给出载体伪经纬度和传统当地经纬度之间的转换关系。

假设载体的位置为S，且其离地高度为h，则根据投影关系容易得到载体相对于伪地球坐标系的位置矢量Rp和相对于地球坐标系的位置矢量Re存在如下的关系：

其中：

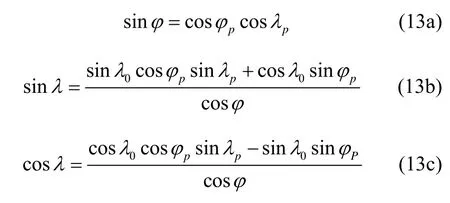
其中：

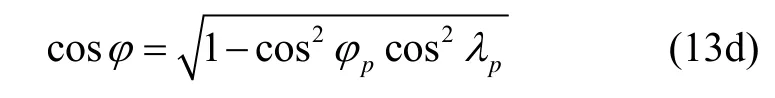
根据式(13)，载体在传统地球坐标系下的位置是容易得到的，进而根据式(8)，传统当地地理坐标系下的捷联矩阵可以根据伪捷联矩阵实时求得。然而对于动基座初始对准，则通常采用外部的速度参考信息做为滤波器观测值，从而在动基座初始对准过程中，导航系统解算出的伪位置是不可避免存在漂移误差。因此由式(13)计算出的载体当地位置是不可避免会受到伪位置误差的影响，进而通过式(8)，可能会影响当地地理坐标系下捷联矩阵的转换精度，从而影响其最终对准结果。因此下面我们将对其分析。

根据式(13)，由导航系统解算的伪经纬度误差引起的当地地理坐标系位置误差为

另外根据式(4)可知，载体的初始伪纬度总为零，并且初始对准通常在一个短时间内完成，因此我们有从而式(14)(15)可以重写为

由式(16)可知，根据式(13)得到的当地经纬度会受到伪位置误差的影响，从而影响惯导系统最终的对准精度。假设惯导系统初始对准完成时，载体的伪经纬度漂移误差都为 100 m，则由于伪位置误差存在，在不同的初始纬度进行对准时，引起的当地经纬度的误差如图2所示。

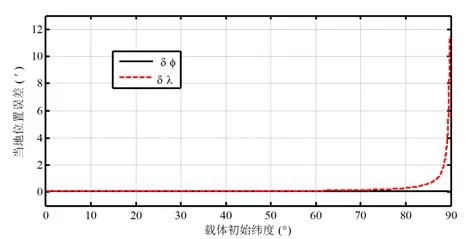
图2 不同的初始纬度下对传统经纬位置误差的影响Fig.2 Position errors for different initial latitudes

由图2可知，在不同的初始纬度进行初始对准时，相同的伪经纬位置漂移误差对当地纬度误差的影响是不会随初始纬度升高而发生改变，而且其影响非常小，可以忽略不记，而对于当地经度位置误差，则会随初始纬度的升高造成不同的影响。在纬度低于 60°的地区，伪经纬度的漂移误差对当地经度误差的影响随着纬度升高变化很小，可以认为是一个常值。100 m的伪经纬位置漂移误差对当地经度位置误差的影响约为0.054′，因此在中低纬度区域，伪经纬位置漂移误差对当地经度误差影响很小，从而通过式(8)引起对捷联矩阵的转换精度影响可以忽略不记。然而在初始纬度高于 60°的地区，伪经纬度的漂移误差对当地经度误差的影响则随着纬度的升高快速增大，特别在极点附近则会趋于无限大，因此在高纬度和极区，伪经纬位置漂移误差对捷联矩阵的转换精度影响必须考虑解决。

根据上面的分析可知，在中低纬度采用伪惯导初始对准算法进行对准时，由伪位置漂移误差造成对捷联矩阵转换精度的影响可以忽略不记，当地地理坐标系的捷联矩阵可以直接由伪捷联矩阵和式(8)实时求得，且不会牺牲其最终对准精度。然而在高纬度和极区，如果直接由式(8)求取当地地理坐标系下的捷联矩阵，则会对最终的对准精度造成影响，特别是在极点附近会造成初始对准的最终结果的失败。然而通过计算，我们容易发现，在初始位置，伪地理坐标系和传统当地地理坐标系之间的转换矩阵是一个常值矩阵，且不受载体初始位置影响。根据式(4)和(9)，在初始位置，传统当地地理坐标系和伪地理坐标系之间的转换矩阵为

由式(17)可知，在任何初始位置，伪地理坐标系和传统南-东-天地理坐标系都是重合的。因此如果初始对准结束时，初始位置的伪捷联矩阵是被得到的，则可以利用式(17)实现地理坐标系和伪地理坐标系之间的转换，从而其不会受到位置误差的影响，进而解决由伪位置漂移误差造成的最终对准精度影响问题。

另一方面，随着导航计算机的发展和其处理能力越来越强大，逆向导航算法已经被提出并用于缩短初始对准的时间，即借助于导航计算机强大的存储能力和处理能力，利用相同的数据段，进行正逆向处理从而加速初始对准过程[14-16]。在此，逆向导航算法不仅可以加速初始对准过程，而且还可以利用存储的数据，逆向计算到初始位置，从而求得载体初始位置的伪捷联矩阵。因此我们可以利用逆向导航的方法，在对准结束时，得到载体初始位置的伪捷联矩阵，进而利用式(17)实现当地地理坐标系下的捷联矩阵和伪捷联矩阵之间的转换，从而可以消除高纬度和极区初始对准精度由伪位置漂移误差带来的影响。然而值得注意的是，在高纬度和极区初始对准中，逆向导航可以解决极区伪惯导初始对准算法动基座初始对准的问题，但是在初始对准结束时，导航系统无法直接进入实时导航状态，仍需要利用存储的数据进行导航解算，计算到当前的时刻，进而进入实时的导航阶段。

综上所述，基于伪地球坐标系的全球动基座初始对准算法的总体方框图如图 3 所示。另外应当注意到，当初始纬度为 90°时，通过伪地球坐标系全球初始对准算法求得的方位角为载体方向与构建伪地球坐标系时所选择的初始经度子午线的夹角。

3 基于伪惯导力学编排的惯导动态误差方程

根据上文的伪惯导系统的导航方程，导航系统的伪姿态、伪速度和伪位置误差方程可以给出

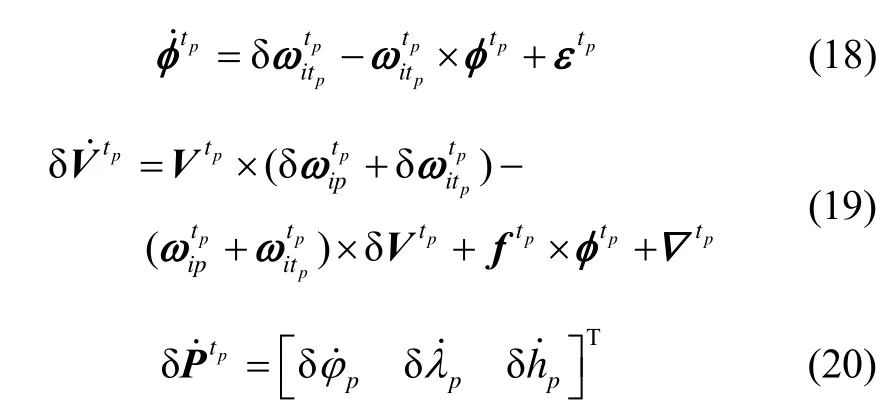
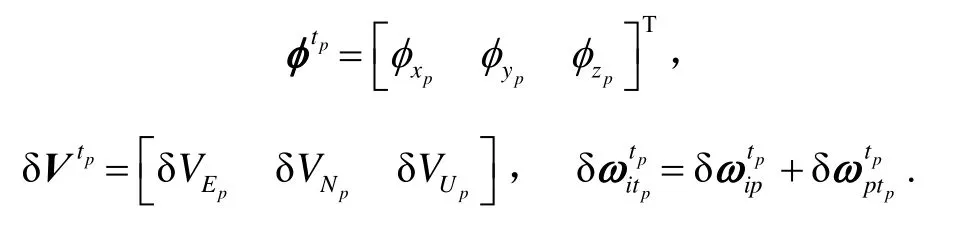
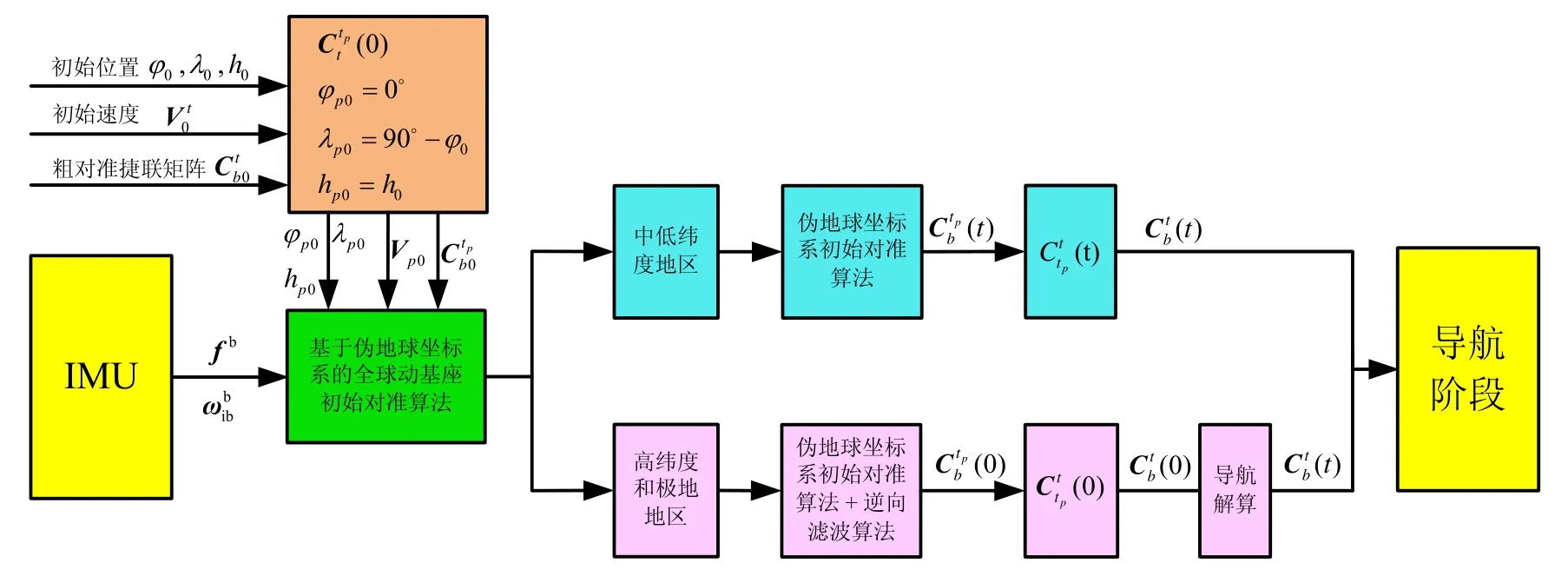
图3 基于伪地球坐标系的全球动基座初始对准方框图Fig.3 Block chart of global initial alignment of moving base with pseudo-Earth frame

另外，由式(4)可知，载体的初始伪纬度总为零，而且通常初始对准会在一个很短的时间内完成，因此有并且动基座对准的姿态误差方程，即式(18)可重写为

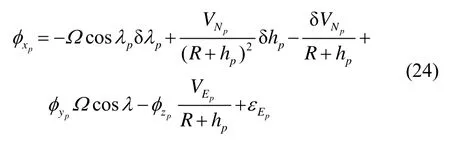
由式(24)～(26)可知，伪惯导力学编排消除了线性运动误差对姿态误差影响成纬度正切函数增加的项，从而可以解决极区初始对准惯导建模的问题。另外由于伪地球坐标系是根据载体初始位置构建的，故其可以在全球范围内消除由惯导建模带来的初始对准问题。因此伪惯导算法不仅可以提高中低纬度的初始对准性能，也可以解决高纬度和极区初始对准建模的问题。故采用伪惯导初始对准算法实现捷联惯导全球动基座初始对准，可以消除由惯导建模造成对全球初始对准性能的影响，进而也可以对全球初始对准算法的惯导编排方案进行统一，且不影响其对准精度，从而更有利于工程的实施与实现。

4 仿真与分析

为了验证伪惯导全球初始对准方案的可行性，本节分别对低纬度和极区动基座卡尔曼滤波初始对准进行仿真验证。

4.1 低纬度动基座初始对准仿真

为了验证伪惯导全球初始对准算法在低纬度时仍具有优良的性能，本节将使用低纬度地区的初始对准仿真对其验证。仿真参数设置如下：初始位置0φ=20°，0λ=126°；载体的真实姿态角θ=γ=ψ=0°；陀螺常值漂移为0.01 (°)/h，随机游走系数为0.001 (°)/h；加速度计常值零偏为1×10-4g，随机游走系数为1×10-5g；载体以10 m/s航速沿载体艏向方向航行10 min。设捷联惯导粗对准的失准角为xφ=yφ=0.3°，zφ=3°，初始速度误差为初始位置误差皆为 1 m，并以载体系的外部参考速度作为滤波器的观测量(由于载体系的外部速度参考是容易获得的，例如多普勒、GPS、Beidou等)，分别使用传统指北惯导初始对准算法和伪惯导初始对准算法来完成捷联惯导卡尔曼滤波动基座初始对准，则其仿真结果如图4所示。图中，实线表示为传统对准算法的对准结果；虚线则为伪惯导对准算法得到的结果，其对准结果是根据式(8)实时转换得到。

由图 4可知，在低纬度采用伪惯导系统进行初始对准时，它具有与传统初始算法相同是收敛趋势，且最终的对准结果基本也是相同的，甚至采用伪惯导算法的对准误差更小。采用两种方法进行初始对准的方位失准角误差分别为-0.3819′和-1.37′。因此伪惯导初始对准算法可以用于低纬度初始对准，而且采用直接实时的转换方法也不会牺牲其对准精度，从而伪惯导初始对准算法为全球动基座初始对准算法的统一提供了可能。

图4 在低纬度的初始对准结果Fig.4 Results of initial alignment at low latitude regions

4.2 极区动基座初始对准仿真

为了验证伪惯导初始对准算法具有全球对准能力，本节将通过极区动基座对准仿真来对其进行验证。由于在高纬度和极区进行初始对准时，地球自转水平分量会变得越来越小，从而使方位失准角的可观测性变得更低，因此载体坐标系下的外部参考信息是无法完成极区初始对准的，故需要采用表达在导航坐标系的外部观测信息来完成高纬度和极区的动基座初始对准。另外惯导系统的初始对准精度不仅与陀螺的常值漂移成正比，而且与载体的初始纬度也有关。随着纬度升高，其对准精度会下降，故在极区对准中选用了较高精度的惯性测量单元。其仿真参数设置如下：初始位置0φ=90°，0λ=126°；载体的真实姿态角θ=γ=ψ=0°；陀螺常值漂移为0.001 (°)/h，随机游走系数为0.0005 (°)/h；加速度计常值零偏为1×10-5g，随机游走系数为5×10-6g；载体以10 m/s航速沿载体艏向方向航行10 min。设捷联惯导粗对准的失准角为初始速度误差为初始位置误差皆为1 m，并以表达在导航坐标系的外部参考速度作为滤波器的观测量。则根据上文提出的基于伪地球坐标系的全球动基座初始对准算法，采用伪惯导初始对准算法+逆向对准滤波算法来完成极区的动基座初始对准。对于逆向对准滤波算法可以缩短对准时间，文献[14][15]已经对其进行了详细的说明，故在此基于伪惯导的极区动基座初始对准仿真中仅采用一次逆向滤波过程，则其对准结果和伪导航系统的伪位置解算结果如图5和图6所示。

图5 极区动基座对准结果Fig.5 Results of alignment with moving base in polar regions

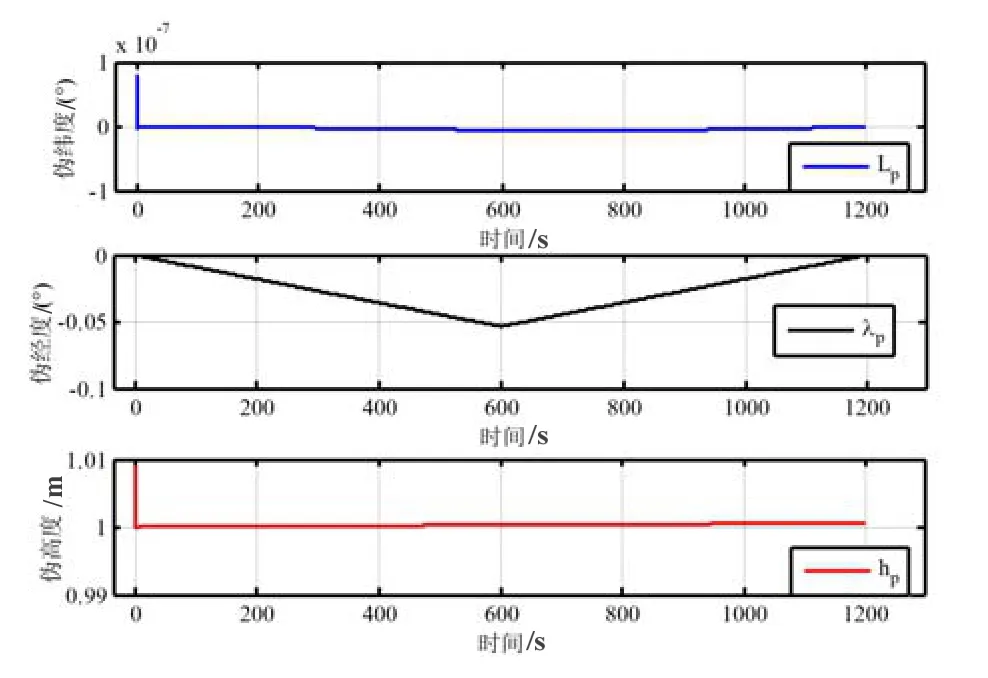
图6 对准过程中的解算伪位置的变化Fig.6 Variation of calculated pseudo position during initial alignment.

由图 5可知，尽管载体的初始纬度为 90°，本文所建议的对准算法仍具有较好的对准结果，因此基于伪地球坐标系的动基座初始对准算法可以解决高纬度和极区的初始对准由惯导建模造成的问题。另外由图6可知，在逆向对准滤波过程中，伪惯导系统的伪位置解算返回到了初始位置，故在对准结束时，其在初始位置的伪捷联矩阵可以被得到，进而根据伪地理坐标系和地理坐标系在初始位置的转换关系得到当地地理坐标系下的捷联矩阵，且不受位置误差的影响。另外，由式(17)可知，初始转换矩阵是一个已知的常值矩阵，故通过初始变换矩阵得到当地地理坐标系下的捷联矩阵也是非常容易实现的。因此基于伪地球坐标系的全球动基座初始对准方案可以有效解决极区初始对准问题，且不会影响其对准精度，进而也可以对捷联惯导的全球初动基座始对准算法进行统一。

5 结 论

为了在全球范围内消除由惯导建模原因造成对捷联惯导动基座初始对准的影响，并期望探索一种统一惯导编排的全球初始对准算法，本文提出了采用伪地球坐标系的惯导编排方案来实现惯导系统的全球动基座初始对准。在中低纬度，惯导系统当地地理坐标系下的捷联矩阵可以根据伪捷联矩阵和其之间的转换矩阵实时的求得，且不会牺牲其对准精度；在高纬度和极地地区则采用伪惯导初始对准算法+逆向滤波算法的方法来获得载体在初始位置的伪捷联矩阵，从而根据初始位置的伪捷联矩阵和初始转换矩阵求得惯导系统在初始位置的当地地理坐标系下的捷联矩阵，且不会受到位置漂移误差的影响。由于初始转换矩阵是一个已知的常值矩阵，故在初始位置，其转换逻辑是非常简单，且容易实现。另外逆向滤波算法也仍可以加速初始对准的过程。最后通过仿真对本文所提基于伪地球坐标系的捷联惯导全球动基座初始对准算法进行验证，结果表明该算法可以有效解决由惯导建模原因造成的全球初始对准的问题，进而为全球动基座初始对准算法的统一提供了可能。

（References）：

[1]Li J, Song N F, Yang G L, et al.In-flight initial alignment scheme for radar-aided SINS in the arctic[J].IET Signal Processing, 2016, 10(8): 990-999.

[2]Salychev O S.Applied inertial navigation: problems and solution[M].Moscow: BMSTU Press, 2004.

[3]Wu Y X, Zhang H L, Wu M P, et al.Observability of strapdown INS alignment: a global perspective[J].IEEE Transactions on Aerospace & Electronic Systems, 2012,48(1): 78-102.

[4]Silson P M G.Coarse alignment of a ship’s strapdown inertial attitude reference system using velocity loci[J].IEEE Transactions on Instrumentation & Measurement,2011, 60(6): 1930-1941.

[5]孙枫, 杨祥龙, 奔粤阳, 等.基于逆坐标系的极区传递对准技术研究[J].弹箭与制导学报, 2014, 34(4): 179-182.Sun F, Yang X L, Ben Y Y, et al.Polar transfer alignment research based on inverse coordinate system[J].Journal of Projectiles Rockets Missiles & Guidance, 2014, 34(4):179-147.

[6]吴枫, 秦永元, 张金亮.极区内基于雷达辅助的SINS空中对准算法[J].西北工业大学学报, 2014(1): 131-136.Wu F, Qin Y Y, Zhang J L.In-flight alignment algorithm for radar aided SINS in polar regions[J].Journal of Northwestern Polytechnical University, 2014, 32(1): 131-136.

[7]Cheng J H, Wang T D, Guan D X, et al.Polar transfer alignment of shipborne SINS with a large misalignment angle[J].Measurement Science & Technology, 2016,27(3): 035101.

[8]周琪, 岳亚洲, 张晓冬, 等.极区飞行间接格网惯性导航算法[J].中国惯性技术学报, 2014, 22(1): 18-22..Zhou Q, Yue Y Z, Zhang X D, et al.Indirect grid inertial navigation mechanization for transpolar aircraft[J].Journal of Chinese Inertial Technology, 2014, 22(1): 18-22.

[9]刘猛, 高延滨, 李光春, 等.基于重构伪地球坐标系的捷联惯导初始对准算法[J].中国惯性技术学报, 2016,24(06): 710-715.Liu M, Gao Y B, Li G C, et al.Initial alignment algorithm for SINS based on reconstructed pseudo-Earth frame[J].Journal of Chinese Inertial Technology, 2016, 24(6): 710-715.

[10]吴枫, 秦永元, 周琪.机载武器极区传递对准算法[J].中国惯性技术学报, 2013, 21(2): 141-146.Wu F, Qin Y Y, Zhou Q.Airborne weapon transfer alignment algorithm in polar region[J].Journal of Chinese Inertial Technology, 2013, 21(2): 141-1713.

[11]Gao S S, Wei W H, Zhong Y M, et al.Rapid alignment method based on local observability analysis for strapdown inertial navigation system[J].Acta Astronautica,2014, 94(2): 790-798.

[12]Kang T Z, Fang J C, Wang W.Quarternion-optimization-based in-flight alignment approach for airborne POS[J].IEEE Transactions on Instrumentation & Measurement, 2012, 61(11): 2916-2923.

[13]姚逸卿, 徐晓苏, 童金武.极区间接横向惯性导航方法[J].中国惯性技术学报, 2015, 23(1): 29-34.Yao Y Q, Xu X S, Tong J W.Indirect transverse inertial navigation algorithm in polar region[J].Journal of Chinese Inertial Technology, 2015, 23(1): 29-34.

[14]Gao W, Ben Y Y, Zhang X, et al.Rapid fine strapdown INS alignment method under marine mooring condition[J].IEEE Transactions on Aerospace & Electronic Systems, 2011, 47(4): 2887-2896.

[15]Chang L B, Hu B Q, Li Y.Backtracking integration for fast attitude determination-based initial alignment[J].IEEE Transactions on Instrumentation & Measurement,2015, 64(3): 795-803.

[16]Gao W, Lu B F, Yu C Y.Forward and backward processes for INS compass alignment[J].Ocean Engineering, 2015,98: 1-9.

Initial alignment algorithm with moving base for SINS based on pseudo-Earth frame in global regions

LIU Meng, GAO Yan-bin, LI Guang-chun, MENG Qing-wen, MA Wen-xia
(College of Automation, Harbin Engineering University, Harbin 150001, China)

One of major problems for achieving the initial alignment of strapdown inertial navigation system (SINS) in global regions is that the SINS navigation errors are enlarged sharply with the increase of latitude, which is caused by the SINS modeling.Although different SINS mechanizations are applied to achieve the global initial alignment, it would be disadvantageous to achieve a unified global alignment algorithm.In addition, the static alignment would also not be achieved in or near the North/South pole since the horizontal component of the Earth rotation decreases to zero gradually.And the moving-base alignment would be advantage to improve the quick reaction capability of SINS.As a result, a novel moving-base alignment algorithm, which is based on pseudo-Earth frame, is proposed to achieve the initial alignment in global regions.The proposed algorithm can eliminate the influence of alignment model on the performance of initial alignment caused by SINS modeling in the global regions and is expected to unify the polar alignment algorithm as much as possible.Finally, the feasibility of the algorithm is demonstrated by simulation.

polar alignment; global initial alignment; SINS; moving-base alignment

U661.1

A

1005-6734(2017)05-0585-07

10.13695/j.cnki.12-1222/o3.2017.05.006

2017-06-12；

2017-08-29

中国国家科学技术部国际科技合作项目（2014DFR10010）

刘猛（1988—），男，博士研究生，从事惯性技术研究。E-mail: liumeng_0304@163.com

联 系 人：高延滨（1963—），男，教授，博士生导师。E-mail: gaoyanbin@hrbeu.edu.cn