车辆动力学模型辅助的惯性导航系统
2017-12-02张月新王立辉汤新华
张月新,王立辉,汤新华
(东南大学 仪器科学与工程学院微惯性仪表与先进导航技术教育部重点实验室,南京 210096)
车辆动力学模型辅助的惯性导航系统
张月新,王立辉,汤新华
(东南大学 仪器科学与工程学院微惯性仪表与先进导航技术教育部重点实验室,南京 210096)
为提高车辆导航系统的精确度和可靠性,提出一种车辆动力学模型辅助惯性导航系统的方法。建立车辆非线性动力学模型,利用四阶龙格库塔法实时解算速度信息。以惯导误差方程为状态方程,动力学模型与惯性导航解算的速度差为观测量,设计了容积卡尔曼滤波器,并用估计的状态误差对惯导进行校正。仿真结果表明,所提出的利用车辆动力学模型辅助惯导的方法能有效抑制惯导误差的发散,位置精度和速度精度比纯惯导系统提高了一个数量级,航向角精度提高了73%。
惯性导航系统;车辆动力学模型;容积卡尔曼滤波;组合导航
惯性导航系统(Inertial navigation system, INS)具有信息量丰富、自主性等优势,但INS导航误差随时间积累,无法长时间单独定位[1]。卫星导航系统用于辅助 INS应用最广,但自主性差,在其失效阶段,组合导航系统只能依赖INS工作,无法保证车辆导航系统长时间工作的精度[2-3]。而车辆动力学模型(Vehicle dynamic model, VDM)对载体状态估计,不需依赖外部条件,具有较强的自主性和适用性[4],可以利用VDM有效地辅助INS进行导航。
目前,基于VDM的车辆状态估计主要有两类,一类是以速度为已知量,利用非线性VDM对侧偏角等状态进行估计[5-6],该类方法对速度的精度要求较高。第二类是以轮胎力为已知量,基于扩展卡尔曼滤波器、一阶斯梯林插值滤波器、递推最小二乘法滤波器,估计车速、横摆角速度、质心侧偏角等状态[7-9]。但第二类方法中将非线性模型简化为线性时会造成一定的误差,降低测量精度,并且VDM估计的状态信息没有用于辅助其他导航系统,具有一定的局限性。
针对第二类方法的不足,基于容积卡尔曼滤波器(cubature Kalman filter, CKF)提出VDM辅助INS的组合导航方法。建立车辆三自由度非线性动力学模型,利用四阶龙格库塔法实时解算速度信息。以 INS误差方程为状态方程,VDM与INS解算的速度差为观测量,设计了CKF,并用估计的状态误差对INS进行反馈和输出校正。该方法中所采用的CKF算法无需对状态模型线性化,直接通过非线性系统方程对容积点进行传播,估计精度高。VDM辅助INS的组合导航方法可有效抑制INS导航误差发散,改善车辆导航系统的可靠性。
1 VDM辅助INS的组合导航系统模型
基于CKF的VDM辅助INS的组合导航系统如图1所示,INS根据微惯性器件输出的角增量和比力,利用姿态更新、速度更新和位置更新算法解算车辆的姿态、速度和位置;VDM 以方向盘转角和纵向力为输入量,利用四阶龙格库塔法实时解算载体坐标系的速度,根据INS得到的姿态矩阵转换为导航坐标系下的速度;设计了CKF,以INS和VDM测量的速度之差作为观测量,INS的误差方程为状态方程,估计INS状态误差,并用估计状态误差对INS进行校正。

图1 VDM辅助INS原理图Fig.1 Schematic diagram of VDM aided INS
1.1 INS数值更新算法
INS数值更新算法利用六轴加速度计和陀螺仪测量载体的比力和角增量,根据已知的初始条件,解算出载体当前时刻的导航参数。导航坐标系n采用东北天地理坐标系,载体坐标系b采用右前上坐标系。INS基本方程包含姿态微分方程、比力微分方程和位置微分方程。其中,姿态四元数微分表达式为

式中:Q为姿态四元数;为载体系相对于导航系的角速度;为陀螺输出的载体系相对于惯性系的角速度为地球自转引起的导航系旋转角速度;为载体运动产生的位移角速度;为导航系转换到载体系的姿态旋转矩阵。
比力微分方程为

INS的位置(纬度L、经度λ、高度h)微分方程式如下:

对于在路面上行驶的车辆,可以假设车辆不离开地面,则车辆在载体坐标系下的向上速度等于0,得到其非完整约束条件为

1.2 车辆动力学模型
VDM 利用载体自身的输入量,解算出载体的部分运动参数,如速度、角速率等。VDM 解算结果辅助校正INS的输出,从而构成INS/VDM的组合导航系统,提高车辆导航精度。建立横向、纵向、横摆三自由度非线性车辆动力学模型,忽略左右轮差异后模型可等效简化为前、后车轮分别集中在车辆前、后轴中点而构成的一个自行车模型,如图2所示。为导航坐标系,轴向东,轴向北;为固定在车辆质心上的载体坐标系,轴与载体横轴重合,向右为正,轴与载体纵轴重合,向前为正。

图2 车辆动力学模型示意图Fig.2 Schematic diagram of vehicle dynamic model
据牛顿力学,车辆的动力学模型为



车辆大部分行驶情况下前轮转向角小于 10°,在极限情况下前轮转向角在30°到40°之间,为应用方便通常可假定前轮转向角δf为小角度。将式(6)(7)代入式(5),并考虑到δf是小角度(即且忽略二阶及以上的高阶微量),经整理后可得:

利用方向盘转角传感器和车轮力传感器信息得到车辆动力学模型的控制输入向量通过四阶龙格库塔法求解微分方程(8)可得载体坐标系下车辆的横向速度纵向速度和横摆角速度根据INS解算的姿态矩阵,可得到导航坐标系下由动力学模型计算的速度:

2 VDM辅助INS滤波器设计
2.1 状态方程和量测方程
采用组合导航间接滤波法,综合考虑系统的精度和实时性,误差状态变量包括3个姿态误差、2个速度误差、2个位置误差、3个陀螺常值漂移、2个加速度计常值零偏,即
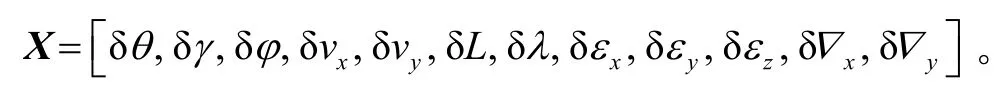
卡尔曼滤波器的状态方程为

式中:A为相应的状态转移矩阵,由INS误差方程构成[10];w为过程噪声。
将INS和VDM解算的东向速度之差、北向速度之差作为卡尔曼滤波器的观测量,即观测向量为则系统的量测方程为

对于式(10)(11)所描述的系统状态方程和量测方程,对其进行离散化,得到k时刻的离散化系统状态模型为
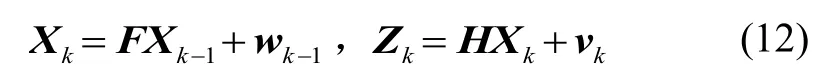
2.2 容积卡尔曼滤波器
CKF采用一组等权值的容积点解决贝叶斯滤波的积分问题,CKF算法具有很好的非线性逼近性能、数值精度以及滤波稳定性[11]。其算法步骤如下:
① 时间更新
1)构造容积点:

2)计算经状态方程传播容积点:
德国罗斯勒公司是生产和销售研磨、抛丸设备的专业厂商,主要产品有研磨光整系统和抛丸清理系统,包括用于发动机、起落架以及机翼等部件的光饰产品和抛丸设备,适于轴类、盘类和叶片的应力强化与抛丸处理。罗斯勒公司创立于1933年,其表面处理技术居世界领先地位,目前已在英国、法国、西班牙、意大利、比利时、奥地利、新加坡、巴西、南非和美国等国家设有分公司,并计划在中国投资建厂。

3)一步预测状态和误差协方差阵:

② 量测更新
1)构造容积点:
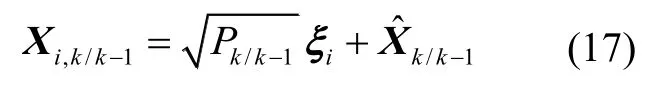
2)计算经量测方程传播容积点:

3)计算观测量预测值:

4)估计新息自协方差矩阵:

5)估计互协方差矩阵:

6)卡尔曼增益矩阵:

7)估计k时刻的状态量:

8)估计k时刻状态误差协方差阵:
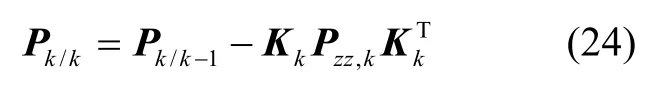
3 仿真验证与分析
Carsim仿真中设置汽车的方向盘转角δ按幅值 60°的正弦规律变化,汽车的纵向速度在不断的加速、匀速和减速变化,方向盘转角和纵向速度随时间的变化过程如图3所示,仿真时长为120 s,采样时间为0.01 s。在不考虑外界因素变化的情况下,对于确定的车辆,参数都是固定的,这些参数不会随着车辆的行驶而变化。当外界因素变化(如车辆的负载变化引起质量m、Iz的变化)时,若将参数m、Iz当作常量,会影响测量精度,此时可根据实际需求,增加测量m的传感设备,通过四阶龙格库塔法求解微分方程(8)时利用实时更新的参数m、Iz,可以保证车辆导航的精确性。仿真实验车辆是一个前轮转向的四轮车,不考虑外界因素的变化,其主要参数如下:

方向盘传动比为 20。设定车辆动力学模型中 3个外输入传感器的量测噪声为均值是0,方差分别为0.5°、20 N、20 N的高斯白噪声。初始纬度为32.0586°,经度为118.7869°,高度为0 m,初始速度和姿态为零,陀螺常值漂移为0.01 (°)/s,角度随机游走为加速度计常值漂移为速度随机游走为

图3 Carsim仿真设置Fig.3 Simulation settings of Carsim
根据上述设置,对INS和INS/VDM组合导航进行数值仿真研究,仿真结果如图4~6所示。其中标注为“真实值”的曲线表示真实结果,标注为“INS”的曲线表示纯惯性导航系统解算的结果,标注为“INS/VDM”的曲线表示动力学辅助导航系统修正解算的结果。图4中分别是经度、纬度和行驶轨迹的对比图。可以看出,运行30 s后INS测量的经度偏离真实值增大,120 s时间内经度的最大偏差为0.43′,纬度最大偏差为0.15'。INS/VDM组合导航的运行轨迹和真实轨迹吻合度高,经度、纬度的最大偏差分别为0.006′和0.01′。图5中分别为东向速度和北向速度的导航速度对比图,INS测量的东向速度偏差较大,经INS/VDM组合导航改善后,最大东向速度误差由14.7 m/s降低到0.6 m/s,最大北向速度误差由8.52 m/s降低到0.84 m/s。从图6航向角对比图可以看出,最大航向角误差降低了78.4%。VDM辅助INS的组合导航方法在位置、速度和姿态上均有明显的改善效果。表1给出了INS精度和INS/VDM组合导航系统精度的对比。
由表1可以看出,由于采用的惯性器件精度较低,纯惯导系统误差发散快,INS/VDM 组合导航系统估计的位置和速度精度比INS提高一个数量级,航向角估计精度提高了73%。VDM辅助INS对INS误差的发散有很好地抑制效果。

表1 INS和INS/VDM精度对比Tab.1 Comparison on precisions of INS and INS/VDM

图4 导航位置对比Fig.4 Comparison of navigation positions

图5 导航速度对比Fig.5 Comparison of navigation velocities
4 结 论
针对INS导航误差随时间积累,无法长时间保持导航精度的问题,研究了一种基于CKF的VDM辅助INS的组合导航方法。VDM通过对车辆的力学分析建立车辆运动的微分方程组,采用四阶龙格库塔法对速度、角速率进行解算,自主性和实时性好,无累积误差。组合导航状态模型的观测量是VDM和INS解算的速度差,状态方程是 INS的误差方程,利用 CKF对状态误差进行估计并修正 INS。仿真结果表明,INS/VDM 组合导航系统的位置精度和速度精度比INS提高了一个数量级,航向角精度提高了73%,有效地抑制了INS误差发散,达到了提高车辆导航系统精确度和可靠性的目的。
(References):
[1]李博文, 姚丹亚.低成本车载 MEMS惯导导航定位方法[J].中国惯性技术学报, 2014, 22(6): 719-723.Li B W, Yao D Y.Low-cost MEMS IMU navigation positioning method for land vehicle[J].Journal of Chinese Inertial Technology, 2014, 22(6): 719-723.
[2]Gao N, Zhao L.An integrated land vehicle navigation system based on context awareness[J].GPS Solutions,2016, 20(3): 509-524.
[3]Quinchia A G, Falco G, Falletti E, et al.A comparison between different error modeling of MEMS applied to GPS/INS integrated systems[J].Sensors, 2013, 13(8): 9549.
[4]Skog I, Ndel P.In-car positioning and navigation technologies: a survey[J].IEEE Transactions on Intelligent Transportation Systems, 2009, 10(1): 4-21.
[5]Li X, Song X, Chan C.Reliable vehicle sideslip angle fusion estimation using low-cost sensors[J].Measurement,2014, 51(1): 241-258.
[6]Miao Z, Zhang H, Zhang J.A robust method of vehicle stability accurate measurement using GPS and INS[J].Measurement Science Review, 2015, 15(6): 294-303.
[7]Nam K, Fujimoto H, Hori Y.Lateral stability control of in-wheel-motor-driven electric vehicles based on sideslip angle estimation using lateral tire force sensors[J].IEEE Transactions on Vehicular Technology, 2012, 61(5):1972-1985.
[8]Lian Y F, Zhao Y, Hu L L, et al.Cornering stiffness and sideslip angle estimation based on simplified lateral dynamic models for four-in-wheel-motor-driven electric vehicles with lateral tire force information[J].International Journal of Automotive Technology, 2015, 16(4): 669-683.
[9]Kanghyun N.Application of novel lateral tire force sensors to vehicle parameter estimation of electric vehicles[J].Sensors, 2015, 15(11): 28385-28401.
[10]王丽芬, 杨功流, 单友东, 等.车载定位定向系统误差在线补偿方法[J].中国惯性技术学报, 2015, 23(2): 145-149.Wang L F, Yang G L, Shan Y D, et al.On-line errorcompensation of vehicular position and orientation determination system[J].Journal of Chinese Inertial Technology, 2015, 23(2):145-149.
[11]Arasaratnam I, Haykin S, Hurd T R.Cubature Kalman filtering for continuous-discrete systems: theory and simulations[J].IEEE Transactions on Signal Processing,2010, 58(10): 4977-4993.
Vehicle dynamic model aided inertial navigation system
ZHANG Yue-xin, WANG Li-hui, TANG Xin-hua
(Key laboratory of micro-inertial instrument and advanced navigation technology, Ministry of education,School of instrument science and engineering, Southeast University, Nanjing 210096, China)
To improve the accuracy and reliability of the vehicle navigation system, an inertial navigation system aided by vehicle dynamic model is proposed.A nonlinear dynamic model of the vehicle is established and a fourth-order RungeKutta algorithm is used to calculate the velocity in real time.The error equation of the inertial navigation system is the state equation, and the calculated velocity difference between the vehicle dynamic model and inertial navigation is the observation vector.Then a cubature Kalman filter is designed,and the estimated state error is used to compensate the inertial navigation system.Simulation results show that the proposed method can effectively suppress the divergence of the inertial navigation error.The accuracies of the estimated position and velocity are both one order higher than those of the pure inertial navigation system, and the accuracy of the estimated yaw angle is improved by about 73%.
inertial navigation system; vehicle dynamic model; cubature Kalman filter; integrated navigation system
V249.32
A
1005-6734(2017)05-0576-05
10.13695/j.cnki.12-1222/o3.2017.05.004
2017-05-24;
2017-08-29
国家重点研发计划(2016YFD0702000);国家自然科学基金(61773113,51477028,41704025);江苏省自然科学基金(BK20160668)
张月新(1990—),女,博士研究生,从事组合导航研究。E-mail: smileyuexin@163.com
联 系 人:王立辉(1979—),男,博士生导师,教授,从事导航、精密仪器等方面的应用研究。E-mail: wlhseu@163.com
