基于极大似然准则的INS/GNSS组合导航自适应UKF滤波算法
2017-12-02胡高歌高社生高兵兵
王 维,胡高歌,高社生,高兵兵
(西北工业大学 自动化学院,西安 710072)
基于极大似然准则的INS/GNSS组合导航自适应UKF滤波算法
王 维,胡高歌,高社生,高兵兵
(西北工业大学 自动化学院,西安 710072)
为提高INS/GNSS组合系统对过程噪声方差不确定性的鲁棒性,提出一种基于极大似然准则的自适应 UKF算法。在该算法中,首先利用新息向量的统计信息构造量测向量的后验概率密度,然后通过极大似然准则在线求取过程噪声方差的估值,并将其反馈至 UKF滤波过程,用于调整卡尔曼增益矩阵。提出的算法可以抑制过程噪声方差不确定性对滤波解的影响,克服了 UKF的缺陷。仿真结果表明,当过程噪声的标准差增大为其真实值的4倍时,相比于UKF,提出方法的导航精度可至少提高45.5%;相比于ARUKF,其导航精度也可至少提高35.7%。跑车实验结果也验证了提出算法的有效性。
INS/GNSS组合系统;无迹卡尔曼滤波;极大似然准则;噪声方差估计
INS/GNSS组合系统兼备了抗干扰性好、自主能力强、定位精度高等优点,已逐渐成为业界应用最为广泛的导航系统之一[1]。当前,INS/GNSS组合系统一般采用卡尔曼滤波对运载体的导航参数进行估计。然而,由于组合导航系统本质上具有非线性特征,当采用非线性的系统模型来更完整地描述导航误差的传播特性时,常规的卡尔曼滤波方法则不再适用[2],此时就需要采用非线性滤波算法来解决导航解算中的状态估计问题[1-3]。
无迹卡尔曼滤波(UKF)借助于 UT变换技术近似计算非线性系统状态的后验概率分布。与扩展卡尔曼滤波(EKF)相比,UKF避免了二阶以上截断误差的引入,具有滤波精度高、鲁棒性强等优点[4]。UKF求解预测值和量测值时需要应用系统模型的采样点信息,但系统模型采样点初始信息的不确定性容易导致滤波器发散,从而使误差变大。对INS/GNSS组合系统而言,由于难以对惯导系统的运动规律进行完全准确的描述,建立的过程模型通常具有近似性[3,5];相反地,基于对导航系统量测设备的先验认知,量测模型往往可以被精确获取[5-6]。因此,通常认为INS/GNSS组合导航系统的不确定因素存在于过程模型中[6],其中,作为系统主要先验信息的过程噪声方差(Q)对UKF的估计精度和稳定性有着重要影响。
为了克服 UKF的缺陷,文献[7]根据新息向量的正交性原理,构建了一种基于多重渐消因子的 UKF非线性滤波器,在一定程度抑制了过程模型不确定性对滤波解的影响,然而,该算法本质上的次优性约束了其滤波精度的进一步提高。文献[8]从协方差匹配原理出发,设计了一种可在线估计系统噪声方差的自适应UKF,然而,由于对噪声方差的估计存在稳态偏差,所以该算法滤波精度不高。文献[9]将自适应滤波的思想与抗差 UKF结合,提出一种自适应抗差 UKF(ARUKF),该算法有效的解决了滤波的发散问题,然而,该算法选取的状态相关因子具有随机性,难以适应组合导航系统的动态环境。
本文针对 INS/GNSS组合系统过程噪声方差(Q)具有不确定性,导致UKF滤波精度降低的问题,提出一种基于极大似然准则的自适应UKF (MLAUKF)。在该算法中,首先利用新息向量的统计信息构造量测向量的后验概率密度,然后通过极大似然准则在线求取过程噪声方差(Q)的估值,并将其反馈至UKF滤波过程,用于调整卡尔曼增益矩阵。提出的MLAUKF能够抑制过程噪声方差不确定性对滤波解的影响,增强了UKF的鲁棒性。以车载INS/GNSS组合系统为例,通过仿真计算和跑车试验对提出的算法性能进行了评估,并与UKF和ARUKF进行了比较。
1 INS/GNSS组合系统数学模型
INS/GNSS组合导航系统利用高精度GNSS信息作为外部量输入,在实际导航解算过程中频繁修正INS,控制其误差积累,从而实现运载器高可靠性的导航定位。
1.1 系统状态方程
取东-北-天地理坐标系(g系)为导航坐标系(n系),并记惯性坐标系为i系,地球坐标系为e系,载体坐标系为b系,计算平台坐标系为'n系。以欧拉平台误差角表示的INS姿态误差方程和速度误差方程可写为[10]


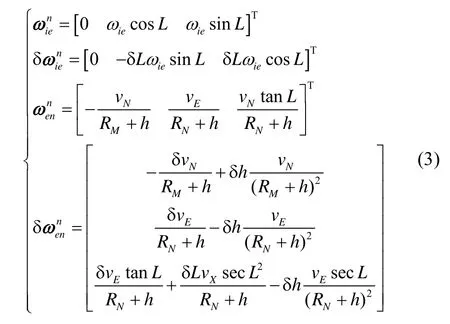
其中:vE和vN为载体的东、北向速度;L和h为载体的纬度和高度;δL和δh为载体的纬度误差和经度误差;RM和RN为地球子午圈和卯酉圈的主曲率半径。
INS的位置误差方程为
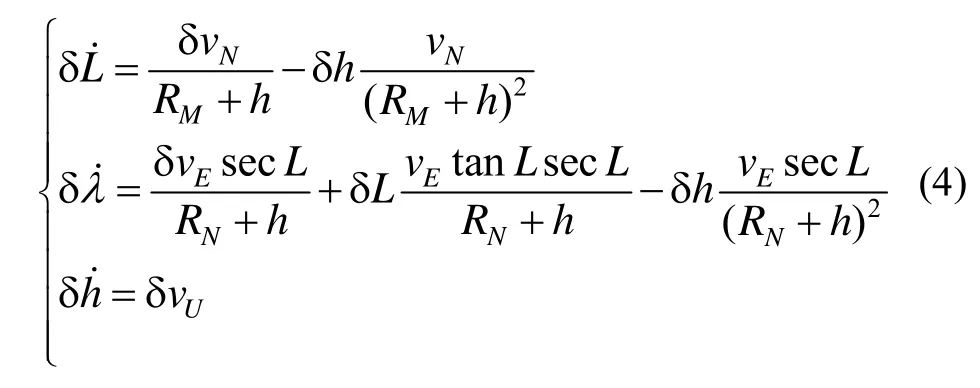
通常条件下,对应于陀螺和加速度计的常值漂移bε与常值偏置可通过随机常数描述[10],即
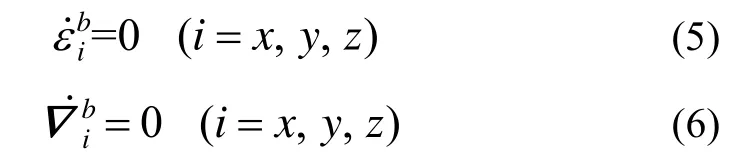
定义系统状态:

根据所定义的系统状态,结合式(1)~(6),可建立INS/GNSS组合系统的状态方程:

1.2 量测模型
以GNSS输出的高精度位置、速度信息为基准,求取INS对应的导航解算误差,可得INS/GNSS组合系统的量测方程为

2 基于极大似然准则的自适应UKF算法
如式(8)所示,INS/GNSS组合系统的过程模型具有非线性特征。采用UKF处理该系统中的状态估计问题时,由于受过程噪声方差(Q)不确定性的影响,UKF得到的导航解会出现精度下降甚至发散的现象。本文提出一种基于极大似然准则自适应 UKF (MLAUKF)来解决这个问题。
2.1 UKF算法
首先简要地给出了UKF算法的基本步骤,以便于实现对MLAUKF的推导。
对式(8)进行离散化处理,并与式(9)组成以下非线性离散系统:
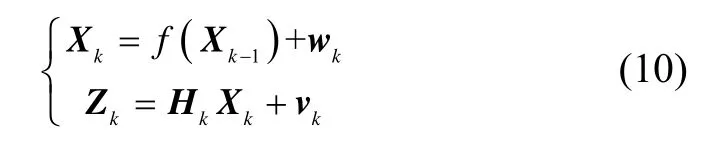
对于非线性系统(10),UKF的计算过程如下:

式中:a为调节参数,控制 sigma点的分布状况;为矩阵均方根的第i列。
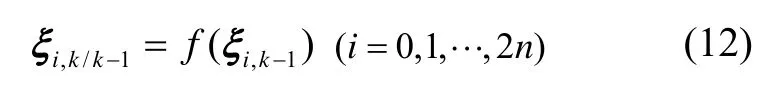
状态预测值及其协方差可更新为

步骤3 量测更新。由于系统量测模型是线性的,量测更新过程与卡尔曼滤波相同:
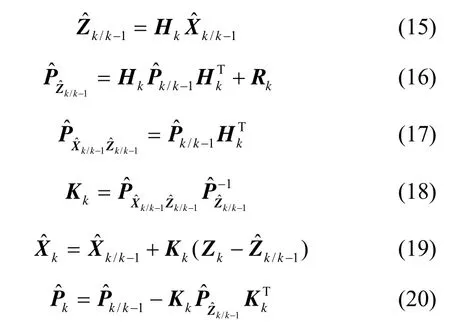
步骤4 返回步骤1,进行下一时刻滤波解算。
2.2 过程噪声方差估计器
本节根据新息向量的统计信息构造了量测向量的后验概率密度,通过极大似然准则对过程噪声方差(Q)进行估计。
记新息向量为

新息向量的协方差可计算如下:

式中,N为平滑窗口的宽度。
在极大似然准则下,量测向量的后验概率密度可表示为[11]

式中,m为量测向量的维数。
对式(23)两侧求对数,可得:
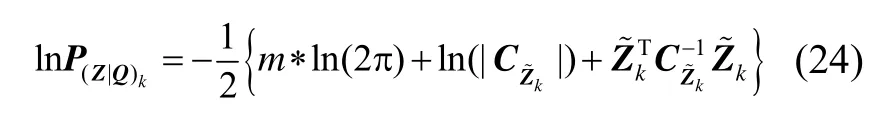
定义代价函数:
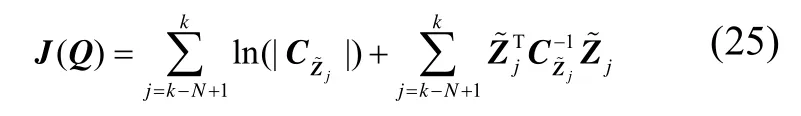
则基于极大似然准则的参数Q的估计值应满足

由式(27)可知,对过程噪声方差Q的估计问题已经转为新息向量的协方差关于Q求导的问题。
定义状态估计误差和预测误差分别为

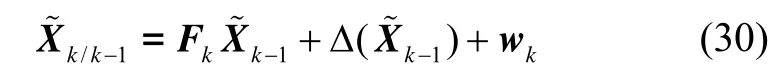
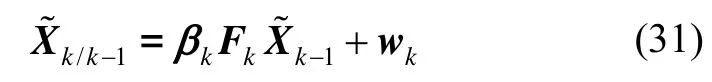
一步预测协方差阵可表示为

此外,由UKF基本公式可知:

对式(32)和(33)关于Q求偏导,有:

当滤波器达到稳态时,式(34)可简化为[12]


结合式(16)~(18)以及(33),可将滤波增益矩阵Kk写为

式(38)可进一步等价表示为

将式(39)和(40)代入(37),并对其进行重组,可得:


另外,由卡尔曼滤波理论可知:
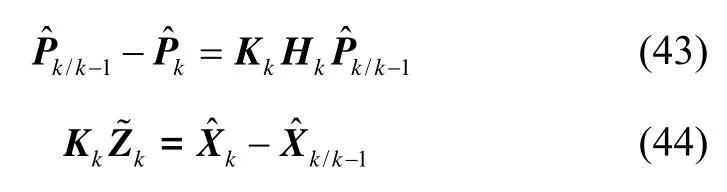
将式(14)(43)(44)代入式(42),可得基于极大似然准则的过程噪声方差估计器为
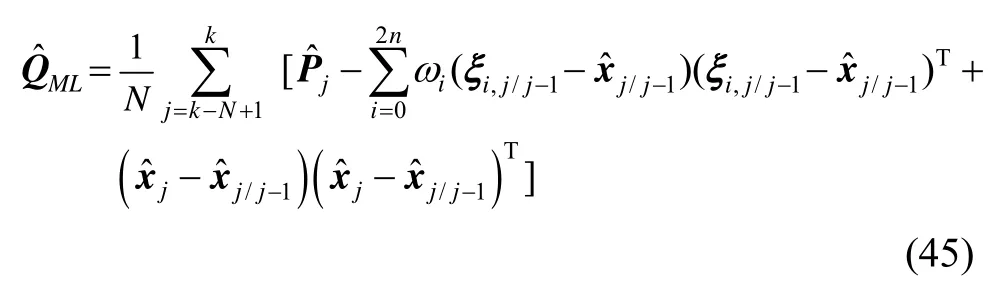
2.3 MLAUKF算法实现
考虑非线性离散系统(10),MLAUKF的主要计算过程如下:
步骤 2 时间更新。根据式(11)~(14)计算状态预测及其协方差阵其中,

步骤 3 量测更新。根据式(15)~(20)计算状态估计及其协方差阵
步骤 5 返回步骤1,开始下一时刻的滤波解算。
3 性能与评估
以车载INS/GNSS组合导航系统为例,通过仿真计算和跑车试验对提出的MLAUKF的性能进行了评估,并与UKF和ARUKF进行了对比。
3.1 仿真计算
假设车辆作机动运动,包括匀速直线、加速直线、变加速转弯、减速等多种状态。模拟的车辆行驶轨迹见图 1。车辆的初始位置为北纬34.246°,东经108.997°,高度500 m;初始速度为10 m/s;初始姿态为方位角0°、俯仰角0°、横滚角0°。陀螺常值漂移为0.1(°)/h,随机游走系数为加速度计常值偏置为随机游走系数为接收机的水平位置误差均方根为3 m,高度误差均方根为5 m,速度误差均方根为0.05 m/s。INS采样频率为20 Hz,GNSS采样频率为1 Hz,仿真时间为1000 s。在MLAUKF中,平滑窗口的宽度取为N=25。

图1 车辆运动轨迹Fig.1 Trajectory of the vehicle
为比较UKF、ARUKF和MLAUKF在过程噪声方差不准确条件下的滤波性能,在仿真的500~1000 s时间段,过程噪声方差被增大为其真实值的16倍。同时,为保证算法的稳定性,在滤波过程中对MLAUKF输出的过程噪声方差估值进行了对角化处理。
图2为MLAUKF对陀螺和加速度计噪声方差(过程噪声方差中的非零值)的估计结果。可以看到,在0~500 s时间段,提出的算法能够有效地实现对过程噪声方差的估计;在500~1000 s时间段,即便过程噪声发生了突变,得到的噪声估值仍能以较快速度收敛到其真实值附近。估计结果证实了提出算法自适应估计过程噪声方差的能力。表1给出了MLAUKF得到的过程噪声方差的均值。

图2 MLAUKF得到的陀螺和加速度计噪声方差估值Fig.2 Estimation of the noise covariance of gyro and accelerometer
图3为采用UKF、ARUKF和提出的MLAUKF计算得到的姿态误差曲线。可以看到:在仿真时间为100~ 500 s时间段,当滤波器稳定时,由于过程噪声方差精确已知,UKF、ARUKF和MLAUKF对姿态角的估计精度相当,得到的方位角、俯仰角和横滚角误差分别在(–0.38′,0.61′)、(–0.25′, 0.26′)和(–0.32′, 0.37′)内;而在500~1000时间段,由于过程噪声方差发生变化,UKF的估计精度明显下降,得到的方位角、俯仰角和横滚角误差分别在(-1.23′, 1.48′)、(-0.76′, 0.63′)和(-0.76′, 0.99′) 内。ARUKF的估计精度UKF稍高,得到的方位角、俯仰角、横滚角误差分别在(-0.91′, 0.82′)、(-0.68′, 0.64′)、(-0.75′, 0.69′)内。然而,由于完全根据经验选取等价权因子和自适应因子,ARUKF的估计结果仍难以令人满意。形成对比的是,MLAUKF得到的相应的姿态误差分别在(-0.58′, 0.53′)、(-0.32′, 0.38′)、(-0.41′, 0.47′)内,精度明显优于UKF和ARUKF。这是因为提出的MLAUKF具有在线估计过程噪声方差的自适应能力。
图4和图5分别为UKF、ARUKF和MLAUKF得到的水平方向的速度和位置误差曲线,其精度对比与姿态误差估计的对比结果类似。在500~1000 s时间段:UKF得到的东向、北向速度误差分别在(-0.33 m/s, 0.26 m/s)和(-0.30 m/s, 0.37 m/s)内,东向、北向位置误差分别在(-20.62 m, 29.29 m)和(-30.59 m, 20.61 m)内;ARUKF得到的东向、北向速度误差分别在(-0.27 m/s,0.29 m/s)和(-0.25 m/s, 0.31 m/s)内,东向、北向位置误差分别在(-20.70 m, 21.96 m)和(-22.90 m, 17.36 m)内;提出的MLAUKF得到的导航精度最高,其东向、北向速度误差分别在(-0.12 m/s, 0.16 m/s)和(-0.16 m/s,0.13 m/s)内,东向、北向位置误差分别在(-9.98 m,10.51 m)和(-13.75 m, 11.12 m)内。

表1 MLAUKF得到的过程噪声方差平均值与真实值的比较Tab.1 The mean estimations of process noise variance by MLAUKF and their corresponding true values
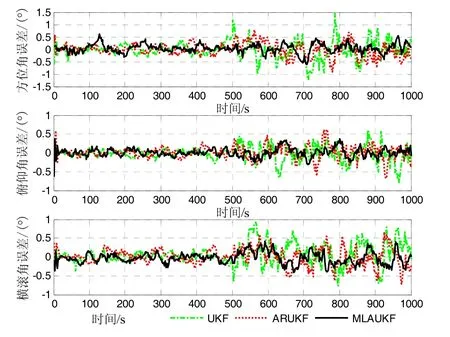
图3 UKF、ARUKF和MLAUKF得到的姿态误差(仿真计算)Fig.3 Attitude errors achieved by UKF, ARUKF and MLAUKF (simulation case)
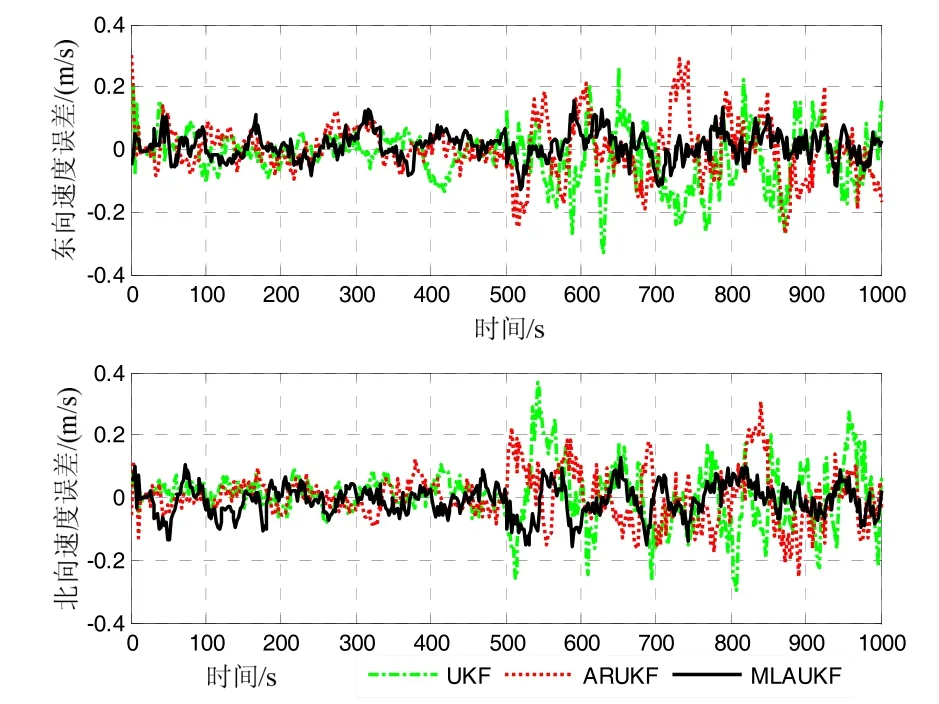
图4 UKF、ARUKF和MLAUKF得到的水平速度误差(仿真计算)Fig.4 Horizontal velocity errors achieved by UKF, ARUKF and MLAUKF (simulation case)

图5 UKF、ARUKF和MLAUKF得到的水平位置误差(仿真计算)Fig.5 Horizontal position errors achieved by UKF, ARUKF and MLAUKF (simulation case)
表2给出了三种滤波算法在500~1000 s内得到的导航参数的均方根误差(Root Mean Square Errors,RMSE)。由统计结果可知,相比于UKF和ARUKF,MLAUKF得到的导航误差分别至少减小了 45.5%和35.7%。

表2 500~1000 s内,UKF、ARUKF和MLAUKF得到的导航参数的均方根误差Tab.2 RMSEs of navigation parameters achieved by UKF,ARUKF and MLAUKF during 500~1000 s
以上仿真结果表明:由于能够在滤波过程中自适应地估计过程噪声方差,进而抑制其不确定性对状态估值的影响,提出的 MLAUKF获得了相比 UKF和ARUKF更高的滤波精度,有效减小了 INS/GNSS组合系统的导航误差。
3.2 实验验证
通过车载导航实验验证了提出的MLAUKF的实用性。实验用车内部布局见图6,其中自制的车载INS/GPS组合系统包括一套NV-IMU300 IMU和一台JAVAD GPS接收机。实验车的行使路线如图7所示,其中:起点位置为东经108.775°,北纬34.030°,高度419m;终点位置为东经108.782°,北纬34.033°,高度417m。实验时间约为970 s,表3表示其车辆行驶状态信息。

图6 实验设备Fig.6 Experimental equipments
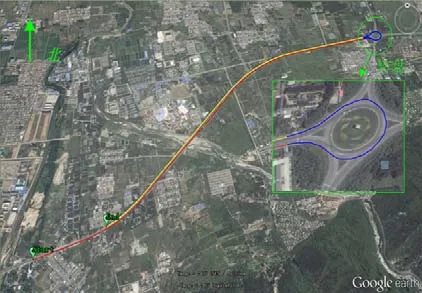
图7 跑车行驶路线Fig.7 Travel route of the experimental car

表3 实验车行驶状态Tab.3 Status of the experimental car
在实验中,陀螺仪、加速度计和GPS接收机的精度参数设置与“仿真计算”部分相同。在MLAUKF中,平滑窗口的宽度取为N=25。

图8 UKF、ARUKF和MLAUKF得到的水平位置误差 (实验验证)Fig.8 Horizontal position error achieved by UKF, ARUKF and MLAUKF (experimental case)
图8为UKF、ARUKF和提出的MLAUKF得到的实验车水平位置误差曲线。可以看到,当实验车静止时(0~150 s和861~970 s),三种算法得到定位误差均小于2.75 m。当实验车沿环山路平稳行驶时(151~490 s和561~860 s),三种算法的定位精度也大致相当,均优于10.69 m。这是因为在以上两种情形下,INS/GPS组合系统的导航解算受过程模型不确定性干扰较小。然而,当实验车沿转盘进行掉头时(491~560 s),由于受到强烈的过程模型不确定性的影响,UKF的滤波精度急剧下降,其水平位置误差仅能控制在(-17.69 m,20.01 m)内。ARUKF能够一定程度地抑制不确定性对导航解的影响,得到的水平位置误差有所减小,但也仅能控制在(-13.77 m, 14.95 m)内。相比之下,提出的MLAUKF由于具有在线估计过程噪声方差的能力,对过程模型不确定性的控制明显增强,得到的水平定位精度在(-10.68 m, 9.25 m)内,显著优于UKF和ARUKF。
表4给出了三种算法在实验车掉头阶段(491~560 s)得到的水平位置误差的平均绝对误差与标准差。能够看出,MLAUKF得到的水平位置误差明显优于另外两种算法,证明了提出的MLAUKF在抑制系统过程模型不确定性方面的优越性。

表4 491~560 s内,UKF、ARUKF和MLAUKF得到的水平位置误差的平均绝对误差与均方根误差(实验验证)Tab.4 MAE and RMSE of the horizontal position errors achieved by UKF, ARUKF and MLAUKF during 461~560 s(experimental case)
4 结 论
本文提出一种基于极大似然准则的自适应UKF,以提高INS/GNSS组合系统对过程噪声方差不确定性的鲁棒性。提出的算法是一种带有过程噪声方差估计器的自适应滤波方法,能够在线估计与调整过程噪声统计,抑制其不确定性对导航解的影响,增强了传统UKF的自适应能力。仿真计算与跑车试验结果表明:在过程噪声方差具有不确定性的条件下,提出算法的滤波性能明显优于UKF和ARUKF,提高了INS/GNSS组合系统的导航精度。
(References):
[1]Hu G G, Gao S S, Zhong Y M.A derivative UKF for tightly coupled INS/GPS integrated navigation[J].ISA Transactions, 2015, 56: 135-144.
[2]薛丽, 高社生, 胡高歌.自适应 Sage-Husa 粒子滤波及其在组合导航中的应用[J].中国惯性技术学报,2013, 21(1): 84-88.Xue L, Gao S S, Hu G G.Adaptive Sage-Husa particle filtering and its application in integrated navigation[J].Journal of Chinese Inertial Technology, 2013, 21(1): 84-88.
[3]Hu G G, Gao S S, Zhong Y M, et al.Modified strong tracking unscented Kalman filter for nonlinear state estimation with process model uncertainty[J].International Journal of Adaptive Control and Signal Processing,2015, 29(12): 1561-1577.
[4]孟阳, 高社生, 高兵兵, 等.基于 UKF的 INS/GNSS/CNS组合导航最优数据融合方法[J].中国惯性技术学报, 2016, 24(6): 746-751.Meng Y, Gao S S, Gao B B, et al.An UKF based multi-sensor optimal data fusion method for INS/GNSS/CNS integration[J].Journal of Chinese Inertial Technology, 2016, 24(6): 746-751.
[5]He X, Wang Z D, Wang X F, et al.Networked strong tracking filtering with multiple packet dropouts: Algorithms and applications[J].IEEE Transactions on Industrial Electronics, 2014, 61(3): 1454-1463.
[6]Chang L B, Li K L, Hu B Q.Huber’s M-estimation based process uncertainty robust filter for integrated INS/GPS[J].IEEE Sensors Journal, 2015, 15(6): 3367-3374.
[7]钱华明, 黄蔚, 孙龙, 等.基于多重次渐消因子的强跟踪 UKF 姿态估计[J].系统工程与电子技术, 2013, 35(3):580-585.Qian H M, Huang W, Sun L, et al.Attitude estimation of strong tracking UKF based on multiple fading factors[J].Systems Engineering and Electronics, 2013, 35(3): 580-585.
[8]Meng Y, Gao S S, Zhong Y M, et al.Covariance matching based adaptive unscented Kalman filter for direct filtering in INS/GNSS integration[J].Acta Astronautica, 2016, 120: 171-181.
[9]Wang Q T, Xiao D, Pang W Y.The research and application of adaptive-robust UKF on GPS/SINS integrated system[J].Journal of Convergence Information Technology, 2013, 8(6): 1169-1177.
[10]孙枫, 唐李军.基于cubature Kalman filter的INS/GPS组合导航滤波算法[J].控制与决策, 2012, 27(7): 1032-1036.Sun F, Tang L J.INS/GPS integrated navigation filter algorithm based on cubature Kalman filter[J].Control and Decision, 2012, 27(7): 1032-1036.
[11]Mohamed A H, Schwarz K P.Adaptive Kalman filtering for INS/GPS[J].Journal of Geodesy, 1999, 73(4): 193-203.
[12]Xu F, Su Y, Liu H.Research of optimized adaptive Kalman filtering[C]//Chinese Control and Decision Conference.2014: 1210-1214.
Maximum likelihood principle based adaptive unscented Kalman filter for INS/GNSS integration
WANG Wei, HU Gao-ge, GAO She-sheng, GAO Bing-bing
(School of Automatics, Northwestern Polytechnical University, Xi’an 710072, China)
A maximum-likelihood based adaptive unscented Kalman filter is presented to improve the robustness of INS/GNSS integrated system against uncertainty of process noise.Firstly, the posterior probability density of the measurement vector is constructed by using the statistics of the innovation vector.Subsequently, the estimation of process noise covariance is obtained based on the maximum-likelihood principle, and are then fed back to the UKF filtering procedure to adjust Kalman gain matrix.The proposed filter has the capability to resist the impact of the process noise covariance uncertainty on filtering solution,overcoming the limitation of the UKF.Simulation results demonstrate that, the navigation accuracy achieved by the proposed method is at least 45.5% higher than that by UKF and 35.7% higher than that by ARUKF, as the standard deviation of process noise is enlarged to four times of its true value.The effectiveness of the proposed filter is also verified via running-car experiment results.
INS/GNSS integrated system; unscented Kalman filter; maximum-likelihood principle; noise covariance estimation
V249.3
A
1005-6734(2017)05-0656-08
10.13695/j.cnki.12-1222/o3.2017.05.017
2017-06-23;
2017-10-07
国家自然科学基金(61174193);高等学校博士学科点专项科研基金(20136102110036)
王维(1984—),男,博士研究生,从事组合导航与非线性滤波算法研究。E-mail: wangweixgd@163.com
联 系 人:高社生(1956—),男,教授,博士生导师,研究方向为导航、制导与控制。E-mail: gshshnpu@163.com
