双航海惯导联合旋转调制协同定位与误差参数估计

王 林，吴文启，魏 国，潘献飞，高春峰

（1.国防科学技术大学 机电工程与自动化学院，长沙 410073；2.国防科学技术大学 光电科学与工程学院，长沙 410073）

双航海惯导联合旋转调制协同定位与误差参数估计

王 林1，吴文启1，魏 国2，潘献飞1，高春峰2

（1.国防科学技术大学 机电工程与自动化学院，长沙 410073；2.国防科学技术大学 光电科学与工程学院，长沙 410073）

单轴/双轴旋转调制航海惯导备份配置满足了舰艇对于定位精度、可靠性、成本的综合要求，但系统间缺少信息融合。针对此问题，以单轴旋转惯导的姿态误差、速度误差、位置误差与双轴旋转惯导对应误差的差值以及两套惯导的陀螺常值漂移、水平加速度计常值零偏为系统状态，并以二者间扣除杆臂效应后的速度及位置的差值为观测量，通过联合旋转调制，改变两套系统 IMU的相对姿态关系。分段常值可观测性分析表明，所有系统状态完全可观。建立了定位误差预测方程，对单轴旋转惯导方位陀螺漂移造成的定位误差进行预测补偿。实验结果表明，对单轴旋转惯导方位陀螺漂移造成的定位误差预测补偿后，其定位误差减小了30%，不仅满足了高可靠性的要求，而且提高了故障情况下的导航精度。

单轴旋转惯导；双轴旋转惯导；协同定位；误差参数估计

为满足各类舰艇对长航时、高精度导航定位的需求，国内外对激光陀螺单轴、双轴(或三轴)旋转惯导进行了深入研究[1-7]。影响高精度激光陀螺惯导精度的误差因素分为确定性误差和随机性误差(主要是陀螺角度随机游走)[1-2,8]。

单轴旋转惯导无法调制方位陀螺漂移的影响，其会造成与时间成正比的定位误差[2,4]；双轴旋转惯导可调制所有陀螺漂移及加速度计零偏的影响，决定其定位精度的主要因素是陀螺的角度随机游走[1,3,5]，其造成的定位误差正比于时间的均方根，相较于单轴旋转惯导而言其定位精度理论上更高，但其结构相对复杂、成本相对更高、可靠性低于单轴旋转惯导[2]。综合考虑定位精度、成本等方面的因素，对可靠性要求很高的舰艇而言，单轴、双轴旋转惯导备份配置是一种合理的方案[2]。通过系统间的信息融合，对单轴旋转惯导方位陀螺漂移造成的确定性误差进行估计和补偿以提高其定位精度，既能保证单轴/双轴旋转惯导备份配置正常情况下的定位精度，又能保证某一设备故障情况下的定位精度，特别是在双轴旋转惯导故障情况下。

文献[9]合理选取系统状态，以两套旋转惯导间的导航参数差值为观测量，利用卡尔曼滤波，估计两套系统的陀螺常值漂移、加速度计常值零偏。以此为基础，本文通过合理地设计联合旋转调制策略，建立单轴旋转惯导和双轴旋转惯导的联合误差状态方程，以系统间扣除杆臂效应后的速度、位置的差值为观测量，实现两套系统陀螺常值漂移、加速度计常值零偏的估计，并对单轴旋转惯导的方位陀螺漂移造成的确定性的长期定位误差进行预测补偿，使得单轴/双轴备份配置的协同定位精度在各种工作条件下都能得到保证。

本文以两套旋转惯导的导航参数输出量的差值为观测量进行滤波器设计，无需改动现有导航系统的导航算法内部架构；对两套系统的相对安装关系没有要求，具有实施简单的优点；实现了舰艇搭载的多套旋转惯导系统间导航信息的融合利用。

1 单轴/双轴旋转惯导联合状态方程

以单轴旋转惯导、双轴旋转惯导的姿态误差、速度误差、位置误差的差值为系统状态，同时增加两套系统各自三个陀螺常值漂移、两个水平方向的加速度计常值零偏作为系统状态，共计17个误差状态：

考虑到船上两套惯导系统安装位置很近，位置、速度、比力的差异很小，则状态方程为

其中：

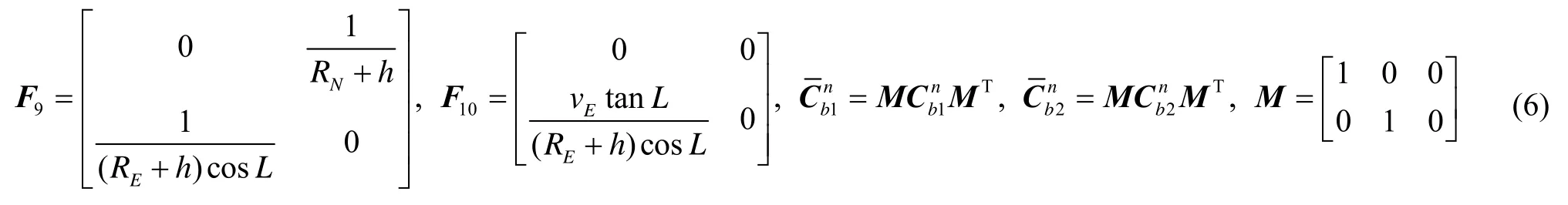
系统噪声为

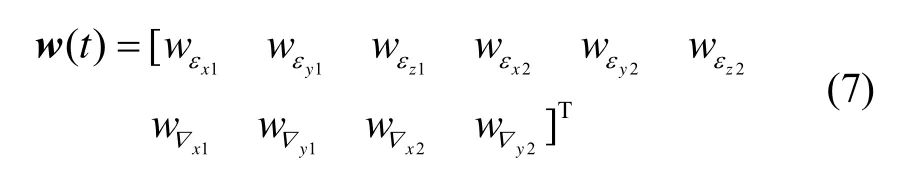
系统噪声驱动矩阵为

其中：单轴旋转惯导体坐标系b1定义为右-前-上；双轴旋转惯导体坐标系b2定义同上；导航坐标系n为当地水平地理坐标系(东-北-天)；分别为单轴/双轴旋转惯导姿态误差差值的东向、北向、天向分量，分别为单轴/双轴旋转惯导的东向、北向速度误差差值，分别为单轴/双轴旋转惯导的纬度、经度误差差值，εx1、εy1、εz1为单轴旋转惯导体坐标系下相应坐标轴的陀螺常值漂移，εx2、εy2、εz2为双轴旋转惯导体坐标系下相应坐标轴的陀螺常值漂移，▽x1、▽y1、▽x2、▽y2为两套系统各自体坐标系下相应水平坐标轴的加速度计常值零偏；w(t)各元素为两套系统各自对应的陀螺、加速度计噪声；高度通道相关的速度和位置误差及加速度计零偏未考虑。

2 观测方程

扣除杆臂造成的相对速度误差，以单轴/双轴旋转惯导间的速度之差、位置之差为相应的观测量：

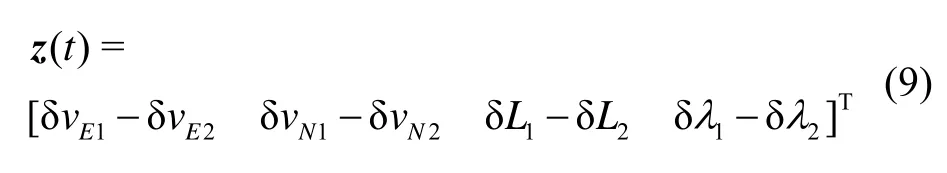
观测方程为

3 联合旋转调制策略编排及可观性分析

根据式(1)～(4)，将单轴/双轴旋转惯导姿态误差差值微分方程写为矢量形式，有：

从式(11)(12)可看出，要实现单轴/双轴旋转惯导各自的陀螺常值漂移从的估计值中分离，关键在于：1）两套惯导系统之间的相对姿态存在变化；2）两套系统各自姿态均需变化。

式中：b1(0)为联合旋转调制开始时刻单轴旋转惯导的载体系，此时转动机构归零；b2(0)为联合旋转调制开始时刻双轴旋转惯导的载体系，此时转动机构归零；单/双轴旋转惯导旋转机构归零时，二者载体系相对水平姿态角0γ、0θ满足小角假设，相对航向角为0ψ；为t时刻单轴旋转惯导相对其初始零位绕方位轴转动的角度；ψ2(t)、γ2(t)为t时刻双轴旋转惯导相对其初始零位分别绕方位轴、横滚轴转动的角度。

将式(14)代入式(13)，有：

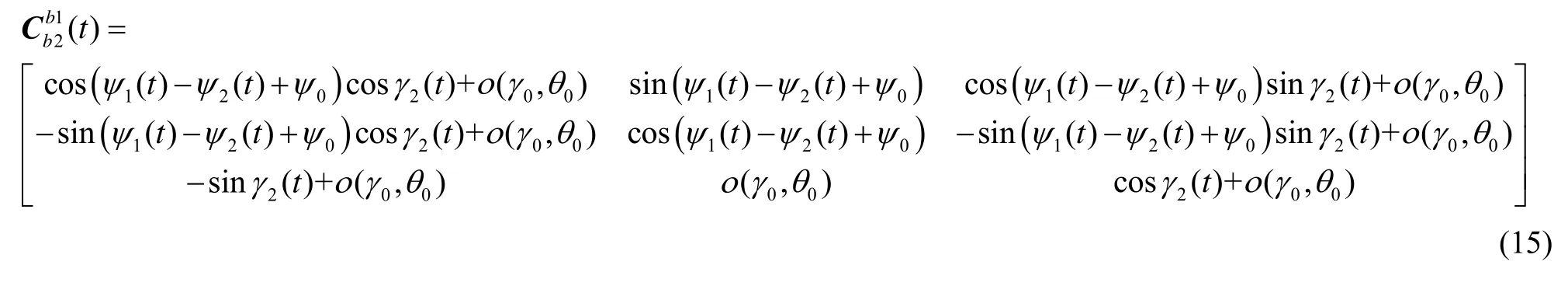
单轴旋转惯导相对其转动机构零位进行 4位置转停，停转角度分别为 0°、90°、180°、270°；双轴旋转惯导分别绕其转动机构横滚轴、方位轴进行16次序转停[5]，两个轴向的停转角度均为0°、180°。若定义b1(t)、b2(t)坐标系间相对航向角、相对横滚角取值定义域分别为则由式(15)可得b1(t)、b2(t)坐标系间相对姿态角取值如表1所示，此处忽略了与0γ、0θ有关的小量的影响。

表1 相对姿态角Tab.1 Relativ e attitude angle

由表1可以看出，b1(t)、b2(t)坐标系间相对姿态角取值可达 4×2=8种情况，包含了方位轴相对姿态角和横滚轴相对姿态角两个轴向的变化。

采用分段线性定常系统可观性分析方法[10]，根据式(2)～(6)(10)，求取系统的总可观性矩阵

若Q(r)满秩，则该系统完全可观。结果表明，通过联合旋转调制策略编排，当单/双轴旋转惯导间的相对姿态矩阵既包含了方位轴相对姿态角的变化，也包含了横滚轴相对姿态角γ2(t)的变化时，满秩，系统状态完全可观。联合旋转调制策略使得单/双轴旋转惯导之间的相对姿态存在变化，实现了各自陀螺常值漂移的分离估计；加速度计常值零偏的分离估计类似。

4 定位误差预测

图1所示为一种单轴/双轴备份配置示意图。通过单轴/双轴旋转惯导系统间的信息融合对各自惯性器件的常值误差进行估计，虽然单轴旋转惯导水平方向的陀螺漂移和加速度计零偏、双轴旋转惯导所有方向的陀螺漂移和加速度计零偏对各自定位的影响均被调制，但可用于监控惯导系统中惯性器件的工作状态以进行故障诊断。正常情况下对单轴旋转惯导方位陀螺漂移进行估计，同时对其造成的确定性的长期定位误差进行预测补偿，补偿方式为输出校正。补偿后的单轴旋转惯导定位误差主要为陀螺角度随机游走造成的随机性误差。单轴旋转惯导的可靠性通常高于双轴旋转惯导[2]，即使双轴旋转惯导出现故障，单轴旋转惯导输出的补偿过确定性误差的定位结果仍能保证较高的定位精度，这样的配置既保证了可靠性，又能保证故障情况下的定位精度，同时节约了成本。

图1 双航海惯导配置Fig.1 Dual MAINS configuration

下面给出单轴旋转惯导的定位误差预测模型。

误差状态为

陀螺漂移、加速度计的零偏输入为

误差状态方程为

其中：

各分块矩阵同式(3)～(6)，离散化式(19)得到误差状态预测方程：

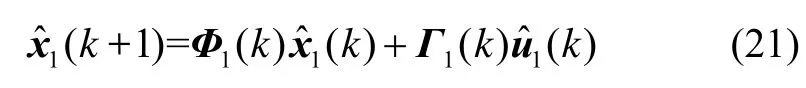
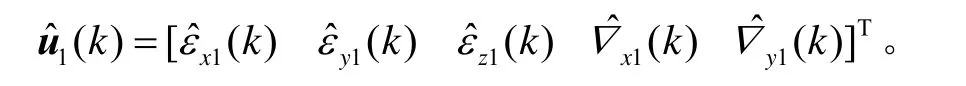
5 仿真分析与实验验证

联合旋转调制策略设置：单轴旋转惯导绕方位轴周期性地进行4位置转停，双轴旋转惯导绕横滚轴、方位轴周期性地进行16次序转停[5]，纬度、经度分别为28.222°N、112.993°E。通过理想噪声条件下半实物仿真实验考察陀螺常值漂移、加速度计常值零偏的估计精度；通过含趋势项噪声条件下的仿真实验考察单轴旋转惯导定位误差的预测补偿情况，在此基础上通过实际实验进行了进一步验证。

5.1 半实物仿真分析一

考察陀螺常值漂移、加速度计常值零偏的估计精度。陀螺、加速度计噪声数据为两套90型高精度激光陀螺航海惯导长时间（120 h）静态测试数据按每5 min求均值，进而减去此均值所得，所得数据作为不包含趋势项（主要为环境温度敏感性误差）的理想噪声数据，该噪声数据可以反映实际惯性器件的噪声水平。陀螺角度随机游走均优于加速度计随机噪声的功率谱密度方根值均优于

陀螺常值漂移、加速度计常值零偏的设定值均假定为单/双轴旋转惯导长时间对准结束时各漂移、零偏项估计补偿后的残余部分。

单轴旋转惯导误差参数：1）εz1的取值为 0.0003(°)/h，εx1、εy1的取值分别为 0.003 (°)/h、-0.002 (°)/h，方位陀螺及水平陀螺常值漂移值的设定以定位精度优于1 nm / 72 h的单轴旋转惯导误差分配方案中对激光陀螺精度的要求为基准[4]；2）▽x1、▽y1的取值分别为（忽略高度通道）。

双轴旋转惯导误差参数：1）εx2、εy2、εz2的取值分别为 0.004 (°)/h、-0.005 (°)/h、0.003 (°)/h；2）▽x2、的取值分别为（忽略高度通道）。

图2、图3分别给出了单/双轴旋转惯导联合状态卡尔曼滤波估计得到的陀螺常值漂移、加速度计常值零偏在前16 h的估计值。单轴旋转惯导水平陀螺常值漂移估计误差及双轴旋转惯导三个陀螺的常值漂移估计误差均优1.0×10-3(°)/h，单轴旋转惯导方位陀螺常值漂移的估计误差优于5.0×10-5(°)/h，所有水平加速度计常值零偏的估计误差在10-6g量级。

从上面的估计误差值可以看出，与单轴旋转惯导的方位陀螺常值漂移估计误差相比，其水平陀螺常值漂移及双轴旋转惯导的陀螺常值漂移估计误差相对较大，主要原因在于：经旋转调制后，单轴旋转惯导的水平陀螺常值漂移及双轴旋转惯导的陀螺常值漂移均被调制掉，其对定位误差的影响不明显，而单轴旋转惯导的方位陀螺常值漂移会造成与导航时间成正比的确定性误差，其影响作用持续存在。

图2 陀螺漂移估计Fig.2 Gyro drift estimation

图3 加速度计零偏估计Fig.3 Accelerometers bias estimation

5.2 半实物仿真分析二

单轴/双轴备份配置情况下，对单轴旋转惯导方位陀螺漂移造成的确定性定位误差进行预测补偿，不仅能够满足高可靠性的要求，同时可以实现系统故障情况(特别是双轴旋转惯导故障)下定位精度的保证。

实际航海惯导系统工作时，陀螺漂移、加速度计零偏虽经过温度补偿，但仍有可能存在未补偿的趋势项。与仿真分析一中的陀螺、加速度计噪声数据产生方式不同，此处陀螺、加速度计噪声数据为三套 90型高精度激光陀螺航海惯导长时间(120 h)静态测试数据整体求均值，进而减去此均值所得。因为是整个测试时间段内求均值进而减去此均值，得到的噪声数据包含了相关趋势项。将其中一套系统的测试噪声数据作为单轴旋转惯导的噪声数据，另外两套系统的噪声数据作为双轴旋转惯导的噪声数据。

单轴旋转惯导分别与两套双轴旋转惯导进行联合状态卡尔曼滤波，并根据单轴旋转惯导的定位误差预测模型对其方位陀螺漂移造成的确定性的定位误差进行预测补偿。两次实验均假定双轴旋转惯导在第36 h故障，故障时刻后由补偿过确定性定位误差的单轴旋转惯导提供导航定位结果。

图4～5为单轴旋转惯导与第一套双轴旋转惯导的实验结果示意图。图4给出了按照定位误差预测模型计算得到的单轴旋转惯导的纬度误差、经度误差预测值，从图中可以看出，该预测模型表现良好，特别是对于单轴旋转惯导方位陀螺漂移造成的正比于时间的定位误差具有较好的预测表现。图5给出了单轴旋转惯导补偿确定性误差前后的径向位置误差对比，补偿过确定性定位误差之后，误差减小了30%以上。作为对比，图中绿色虚线给出了双轴旋转惯导不存在假定故障时的径向位置误差，将其与补偿过确定性定位误差后的单轴旋转惯导定位误差曲线对比可以发现两者精度相当。因此，通过两套系统间的信息融合，提高了故障情况下的导航定位精度。

图6～7为单轴旋转惯导与第二套双轴旋转惯导的实验结果示意图。图6给出了按照定位误差预测模型计算得到的单轴旋转惯导的纬度误差、经度误差预测值，从图中可以看出，该预测模型表现良好。图7给出了单轴旋转惯导补偿确定性误差前后的径向位置误差对比。补偿过确定性定位误差之后，定位精度提升明显，并优于此套双轴旋转惯导的定位精度。出现这种情况的原因在于：单轴旋转惯导补偿过方位陀螺漂移造成的确定性定位误差之后，剩余部分主要是陀螺角度随机游走造成的随机性误差，若其陀螺角度随机游走小于双轴旋转惯导的陀螺角度随机游走，其定位精度将优于双轴旋转惯导的定位精度。

因此，通过两套系统间的信息融合，对单轴旋转惯导的定位误差进行预测、补偿，既满足单轴/双轴旋转惯导备份配置可靠性的要求，又能提高故障情况下的导航定位精度。

图4 单轴旋转惯导位置误差预测Fig.4 Position error prediction of one-indexing MAINS

图5 位置误差对比Fig.5 Position error comparison

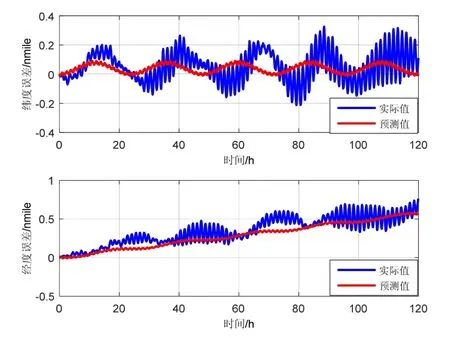
图6 单轴旋转惯导位置误差预测Fig.6 Position error prediction of one-indexing MAINS

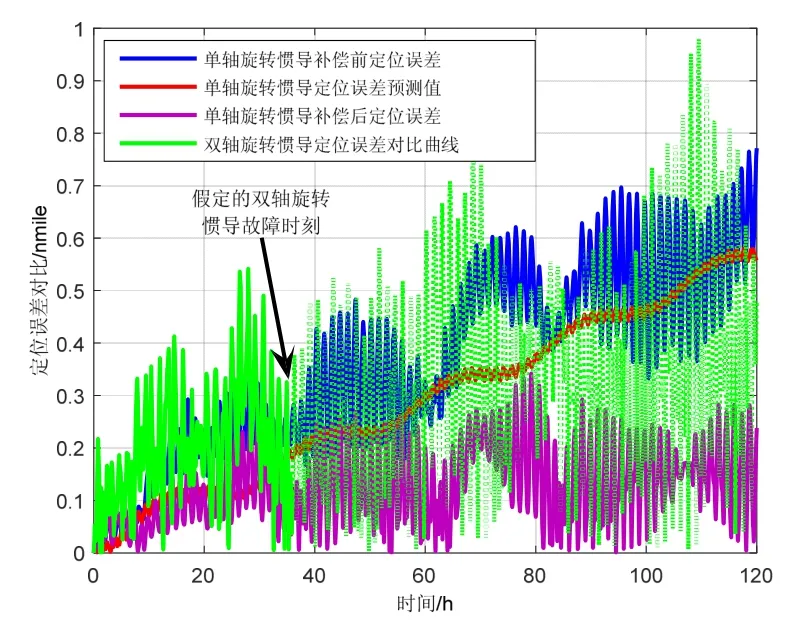
图7 位置误差对比Fig.7 Position error comparison

5.3 实验验证

利用两套 90型高精度激光陀螺航海惯导分别进行单轴旋转调制、双轴旋转调制实验，考察单/双轴旋转惯导备份配置情况下系统间信息融合的有效性，实验时长为144 h（6天）。

假定双轴旋转惯导在第24 h发生故障，故障时刻之后由单轴旋转惯导输出导航定位结果，并对单轴旋转惯导方位陀螺漂移造成的与导航时间成正比的确定性误差进行输出校正补偿。图8给出了单轴旋转惯导纬度误差及经度误差的实际值、预测值（均为量化值），从图中可以看出，定位误差预测效果较好，对其经度误差发散项的预测基本反映了其变化趋势。

补偿单轴旋转惯导定位误差预测值后，剩余部分主要为陀螺角度随机游走造成的随机性误差。图9给出了补偿确定性误差前后单轴旋转惯导的定位误差曲线，从图中可以看出，在144 h导航时间内，补偿前单轴旋转惯导的最大定位误差可达0.8（量化值），单轴旋转惯导的定位误差漂移显著，补偿后单轴旋转惯导的最大定位误差优于0.5（量化值），其定位误差漂移趋势项得到抑制，定位误差减小了30%，与无故障情况下的双轴旋转惯导定位精度相当（绿色虚线给出了不存在假定故障时的双轴旋转惯导的定位误差曲线）。因此，在单轴/双轴旋转惯导备份配置情况下，通过补偿单轴旋转惯导的长期确定性误差，既满足了单轴/双轴旋转惯导备份配置可靠性的要求，又能提高故障情况下的导航定位精度。

图8 单轴旋转惯导位置误差预测Fig.8 Position error prediction of one-indexing MAINS

图9 位置误差对比Fig.9 Position error comparison

6 结 论

本文建立了单轴/双轴旋转惯导的联合状态方程，在对系统状态可观性分析基础上，通过合理地设计联合旋转调制策略，以扣除杆臂效应后单轴/双轴旋转惯导系统间的速度、位置差为观测量，通过卡尔曼滤波实现了两套系统陀螺常值漂移、加速度计常值零偏的分离估计。估计得到的陀螺漂移、加速度计零偏可用于惯导系统惯性器件工作状态的监控。建立了定位误差预测方程，并对单轴旋转惯导方位陀螺漂移造成的确定性的长期定位误差进行预测补偿，当双轴旋转惯导出现故障时，仍能保证高精度的导航定位。

（References）：

[1]Levinson E, Majure R.Accuracy enhancement techniques applied to the marine ring laser inertial navigator (MARLIN)[J].Navigation, 1987, 36(9): 64-86.

[2]Tucker T, Levinson E.The AN/WSN-7B marine gyrocompass/navigator[C]//Proceedings of the 2000 National Technical Meeting of The Institute of Navigation.Anaheim, CA, 2000: 348-357.

[3]魏国.二频机抖激光陀螺双轴旋转惯性导航系统[D].长沙: 国防科学技术大学, 2013: 6-19, 43.Wei G.Research on some key technologies for doubleaxis rotation inertial navigation system with mechanically dithered ring laser gyroscope[D].Changsha: National University of Defense Technology, 2013: 6-19, 43.

[4]于旭东.二频机抖激光陀螺单轴旋转惯性导航系统若干关键技术研究[D].长沙: 国防科学技术大学, 2013: 15, 43.Yu X D.Research on some key technologies for single-axis rotation inertial navigation system with mechanically dithered ring laser gyroscope[D].Changsha:National University of Defense Technology, 2013: 15, 43.

[5]Yuan B L, Liao D, Han S L.Error compensation of an optical gyro INS by multi-axis rotation[J].Measurement Science and Technology, 2012, 23: 025102.

[6]Zheng Z C, Han S L, Zheng K F.An eight-position self-calibration method for a dual-axis rotational inertial navigation system[J].Sensors and Actuators A: Physical,2015, 232: 39-48.

[7]Gao P Y, Li K, Wang L, et al.A self-calibration method for tri-axis rotational inertial navigation system[J].Measurement Science and Technology, 2016, 27: 115009.

[8]Unsal D, Demirbas K.Estimation of deterministic and stochastic IMU error parameters[C]//Proceedings of the Position, Location and Navigation Symposium.Myrtle Beach, USA, 2012: 862-868.

[9]吴文启, 王林, 潘献飞, 等.一种双惯导联合旋转调制导航与在线相对性能评估方法: 中国, 201510390333.4[P].2015-07-06.

[10]Bar-Itzhack I Y, Goshen-Meskin D.Observability analysis of piece-wise constant systems-part I: theory[J].IEEE Transactions on Aerospace and Electronic Systems, 1992,28: 1056-1067.

[11]Wei G, Li G, Wu Y, et al.Application of least squares support vector machine in system-level temperature compensation of ring laser gyroscope[J].Measurement,2011, 44: 1898-1903.

Dual marine INS joint rotation and modulation for cooperative positioning and error parameter estimation

WANG Lin1, WU Wen-qi1, WEI Guo2, PAN Xian-fei1, GAO Chun-feng2
(1.College of Mechatronics Engineering and Automation, National University of Defense Technology,Changsha 410073, China; 2.College of Optoelectronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)

The dual marine inertial navigation system (MAINS) backup configuration, including a oneindexing MAINS and a two-indexing MAINS, can meet the demands of position accuracy, reliability and cost.However, it lacks the information fusion between systems.Using the velocity and position differences between the systems as observations, a Kalman filter is designed with the attitude error, the velocity error,and the position error differences between the two systems as well as the gyro drifts and horizontal accelerometer biases being system states.A joint rotation and modulation method is proposed, whereby the relative attitude between the two IMUs can be changed to make all the states completely observable according to PWCS observability analysis.A position error prediction equation is formulated to estimate and compensate the positioning error caused by z-axis gyro drift of one-axis indexing MAINS, whereby the position accuracy provided by the one-indexing MAINS can be guaranteed.The experiment results show that the one-indexing MAINS position error is reduced by 30% after error compensation, which can satisfy not only the high reliability but also the position accuracy in case of failure.

one-axis indexing MAINS; two-axis indexing MAINS; cooperative positioning; error parameter estimation

U666.1

A

1005-6734(2017)05-0599-07

10.13695/j.cnki.12-1222/o3.2017.05.008

2017-05-26；

2017-09-10

预研基金重点项目（9140A09031815KG01)）；专利申请号（201510390333.4）

王林（1987—），男，博士研究生，从事惯性导航系统研究。E-mail: wanglinshanda@163.com

联 系 人：吴文启（1967—），男，教授，博士生导师。E-mail: wenqiwu_lit@sina.com