考虑突变状态检测的齿轮实时剩余寿命预测

石 慧， 曾建潮,2

(1.太原科技大学 工业与系统工程研究所，太原 030024； 2.中北大学 计算机与控制工程学院，太原 030051)

考虑突变状态检测的齿轮实时剩余寿命预测

石 慧1， 曾建潮1,2

(1.太原科技大学 工业与系统工程研究所，太原 030024； 2.中北大学 计算机与控制工程学院，太原 030051)

为解决齿轮疲劳退化过程中状态突变后剩余寿命难以准确预测问题，提出一种考虑退化突变点检测与剩余寿命预测相关联的齿轮疲劳实时剩余寿命预测新方法。针对齿轮磨损退化过程建立状态空间预测模型，利用接收到的齿轮实时监测振动信息实时更新模型参数，同时对退化过程中的突变状态点进行检测，并根据突变点所提供的寿命信息采用卡尔曼前向滤波及平滑算法结合期望最大化参数估计算法在滤波的同时不断对状态空间模型参数进行修正，改变退化突变后的滤波效果，进行实时状态预测与寿命估计。运用齿轮疲劳寿命试验台的实时监测数据对预测模型进行验证，结果表明利用突变点信息对预测模型进行修正后可以更快的对系统的动态变化进行跟踪，提高预测齿轮退化状态及实时剩余寿命的准确度。

剩余寿命预测；状态空间建模；卡尔曼滤波；突变状态检测；模型修正

齿轮是如汽轮机、离心压缩机、风机等工业部门中应用最为广泛的旋转机械设备传动系统中的关键部件。齿轮啮合受力情况较为复杂，在变工况、变载荷的情况下运行，更容易发生故障。当齿轮发生断齿、齿面疲劳、胶合等故障时，常常会引起整个机械设备灾难性的破坏[1]。同时随着信息传感设备的发展，可对齿轮的运行状态进行实时监测，传统的故障诊断方法虽然可以实现齿轮故障的有效诊断，但存在一定的局限性。因此对齿轮这类易磨损部件的退化状态预测与健康管理已成为业界日益关注的问题。利用接收到的大量实时监测信息更为准确预测系统的退化状态及其剩余寿命，可以提供有关健康状态的关键信息，进而识别和管理故障的发生、规划维修活动，为更合理地制定基于状态的维护维修策略提供依据[2-4]。

齿轮的磨损退化过程是一个动态随机过程。近年来随着信息传感技术的发展，可对齿轮进行实时监测，并利用接收到大量的反映设备退化性能的监测信息进行更准确的剩余寿命预测，因此基于统计学理论和人工智能理论进行剩余寿命预测建模的数据驱动剩余寿命预测方法被广泛应用于齿轮的预测与健康管理领域。它包括状态空间模型、随机滤波模型、自回归滑动平均模型、支持向量机、人工神经网络及其衍生模型和灰色模型等剩余寿命方法。但在系统运行过程中，可监测到的数据往往只是与状态有关的一些间接观测数据，例如振动信号、温度和压力等信号。而且观测数据往往因受到随机噪声的干扰而出现观测误差。根据观测数据构造状态空间模型对系统的状态进行估计与预测可以很好地解决这一问题。卡尔曼滤波是一种线性最优无偏估计器，随着监测数据的增加，滤波精度越来越高，可对突变状态进行跟踪。Gašperin等[5]针对齿轮的磨损退化建立非线性状态方程，进行线性化并采用卡尔曼滤波状态估计。Carr等[6]采用扩展卡尔曼滤波的方式进行设备退化状态及剩余寿命预测。并假设剩余寿命与退化状态之间满足对数关系进而估计剩余寿命分布，并制定预防性替换的维修策略。Sun等[7]采用卡尔曼滤波的方式进行设备剩余寿命预测。提出健康指标(Health Index，HI)的概念，设备新时HI=1，发生故障HI=0。采用时间序列蒙特卡洛仿真(SMC)进行剩余寿命预测。Bressel等[8]提出扩展卡尔曼滤波方式进行质子交换膜燃料电池退化状态预测，但其降低模型不确定度，不能很好跟踪系统的动态变化。

还有一些文献提出了两阶段和多阶段的退化状态预测模型[9]。Lall等[10]考虑针对正常和潜在故障两个退化状态，其中正常状态不进行预测，潜在故障阶段建立卡尔曼预测模型，进行剩余寿命预测。但文中退化阈值是给定的，没有针对退化的突变状态进行识别检测及动态跟踪。Wang等[11]考虑设备连续运行过程，假设已通过各种统计方法检测到退化异常点，分为正常退化和潜在故障两个阶段，认为在潜在故障阶段退化速度增大，仅在此阶段预测退化状态求其剩余寿命。而齿轮的退化过程随着设备负载及工况的变化而变化，开始齿轮啮合阶段与后期磨损加速阶段是复杂多变的多阶段退化过程，没有恒定不变的阶段，难以用一个退化模型来描述。胡昌华等[12]提出了一种多阶段的预测模型，但其仅是根据历史监测数据分段拟合退化模型建立含可变参数的状态预测模型，但在拟合分布过程中需要大量破坏性实验数据，很难收集或成本太高。同时系统运行中其退化状态很难直接测量，李鑫等[13]提出多种退化模式下动态转移的健康状态自适应预测，由健康状态评估及选定的退化阈值决定改变退化模式进而采用不同的剩余寿命预测方式。但其考虑退化阶段时假设已通过统计方法检测出异常突变点，直接基于新的阶段进行寿命预测及维护维修策略的制定，没有考虑检测出异常点后如何根据突变点提供的信息相应改变预测方法以更好地跟踪剩余寿命的动态变化。

在系统实际运行过程中，往往由于其退化磨损过程由渐变、量变发展为突变、质变，导致系统的材料、结构等发生变化，出现退化突变点。突变点后的退化速率增大进而使剩余寿命发生较大变化。突变点是退化状态发生变化的起始点，它所包含的大量剩余寿命信息能够为剩余寿命预测及预防性维护维修策略的制定提供有用信息[14-15]。本文针对齿轮疲劳寿命试验的实时监测数据建立可变参数的系统退化状态空间模型，同时考虑异常点检测与剩余寿命预测的关联性，对齿轮退化过程中的突变状态点进行检测，突变点后采用卡尔曼前向滤波及平滑算法结合期望最大化参数估计算法在滤波的同时不断对未知的系统模型参数进行修正，增加突变点后观测数据的权重，减小突变点之前的监测信息产生的误差。同时利用检测到的突变点信息修正状态初始值及参数初始值的选择，在突变点修正滤波增益，通过大的滤波增益及滤波估计误差改变滤波效果，重新进行状态估计及寿命预测。将基于退化状态突变点检测和剩余寿命的预测进行联合研究，可以利用突变点信息更快的对系统的动态变化进行跟踪，提高齿轮退化状态预测精度。

1 齿轮疲劳试验

1.1疲劳试验台架

齿轮疲劳寿命试验采用了如图1所示的封闭试验台架。试验台的中心距为150 mm，电机转速为1 200 r/min。试验过程对箱体振动、油温和噪音等进行监测。

图1 齿轮试验台架

疲劳试验台原理图如图2(a)所示。本试验共布置11个传感器，主试箱传感器位置图如图2(b)所示。加速度传感器安装在主试箱的轴承座位置，这样可以使得接收到的振动信号的衰减最小[16]，在齿轮箱内安装温度传感器，在主试箱的正上方安装噪声传感器。1#～8#为加速度传感器(1#～4#布置在主试箱轴承座的径向，7#和8#布置在主试箱的轴向，5#和6#布置在陪试箱轴承座的径向)；9#和10#为声传感器，分别布置在主试箱和陪试箱正上方约40 cm处；11#表示温度传感器，布置在主试箱体内，试验中测试润滑油温度。采样频率25.6 kHz，采样时间60 s，采样间隔9 min。本试验中采用常规成组法即恒载的方式进行，转矩为822.7 N·M。当试验齿轮发生断齿时即判定该齿轮失效，如图3所示。

(a) 齿轮试验台架

(b) 主试箱传感器

Fig.2 The schematic of test bench and sensors’ placement scheme of the main gearbox

图3 主试箱齿轮发生故障断齿

1.2试验齿轮的安装

试验中采用材料为合金钢，齿面硬度为58-61HRC的硬齿面齿轮，表面处理为渗碳淬火。采用正反面交错搭接啮合方式(如图4所示)，电机转速为1 200 r/min。主试箱齿轮模数m=3，齿数为z1=z2=50，压力角α=20°，齿宽29 mm，实际工作齿宽13～14 mm；陪试箱齿轮齿数为z3=z4=24，压力角α=20°，工作齿宽20 mm。因而齿轮啮合频率有2个，分别为1 000 Hz(主试箱齿轮)和480 Hz(陪试箱齿轮)。本次实验润滑油采用L-CKC320工业闭式齿轮油。

图4 试验齿轮正反交错搭接安装图

2 特征提取

对齿轮动态监测信息采用有效的方法进行疲劳状态的特征提取是实现状态预测和维护维修的关键[17]。实际应用中很难采集到表示系统特性的直接状态数据，随着传感技术的发展，可接收到准确的振动信号，振动信号分析已成为齿轮疲劳状态特征提取最有效的方法之一。

目前，较常用的振动信号分析方法包括原始时域、包络时域、原始频谱、解调频谱以及细化频谱分析法，好的评价指标不仅能真实地反映齿轮运行过程中状态性能的变化，而且易于计算。本文利用均方幅值(Root Mean Square, RMS)对齿轮磨损退化性能进行衰退评估。均方幅值作为有量纲的统计特征值，不受齿轮个体差异的影响，随疲劳状态改变呈现递增趋势，能较好地反映各采样时刻振动能量动态的变化，而且易于计算。对于每次采样时间Δt长度内，离散随机信号的时间序列均方幅值可表示为：

(1)

式中：Δt为采样时间；Fs为采样频率；n为采样点数，n=Fs×Δt。

3 基于状态空间模型的退化状态建模

在寿命预测中，如何建立一个适当的模型是首要问题。可以通过非线性状态空间建模进行状态估计。模型的一般形式为：

Xt=f(Xt-1)+wt-1

(2)

Yt=h(Xt)+vt

(3)

式中：Xt为t时刻(t≥1)的系统状态向量；f(·)为系统状态转移模型；Yt为t时刻的系统观测向量；h(·)为系统观测模型。式(2)称为状态转移方程，式(3)称为观测方程。系统噪声wt和观测噪声vt服从零均值的高斯分布(其协方差阵为：Var(wt)=Qt，Var(vt)=Rt)。

非线性模型可以很好的描述动态过程及一系列广泛的动态行为。然而，在实际应用中对非线性系统的分析和辨识相对较复杂。式和式在许多情况下，通过采用线性化进行简化，线性化后的状态空间模型为：

Xt=Ftt-1Xt-1+wt-1

(4)

Yt=HtXt+vt

(5)

4 突变状态检测

当系统运行一段时间，退化状态可能发生突变，退化速率增大，退化状态向上偏移，如图5所示。利用突变点信息对预测系统剩余寿命的状态空间模型进行修正时首先需要进行退化状态突变点的检测。突变状态的检测定义为在某些未知时刻检测到随机序列分布发生变化。其广泛应用于计算机网络入侵检测和安全系统以及各类设备的故障检测中。

图5 退化状态偏移的突变状态点检测示意图

累积和控制图(Cumulative Sum, CUSUM)是基于似然比的一种接近最优的非参数化统计方法，对事件的突变状态进行累积，将过程中的小偏移量累加起来，求其累积进而判断是否发生突变。该算法要求的假定条件较少，能有效反映过程变化的灵敏性，非常适合用在系统退化过程中的突变检测[18]。

max(yn-μ0-k)

(6)

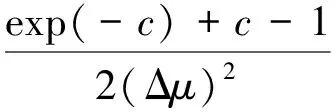
(7)

c=-(Δμ)(h/σ+1.166)=

-2k(h/σ+1.166)

(8)

5 退化状态预测模型修正

如图6所示，假设退化状态不发生突变，A点之后系统退化状态为Ⅰ曲线。但状态突变点A之后退化速率增加，实际退化状态可能变为III曲线。系统接收到大量监测信息，利用累积求和算法(CUSUM)检测到状态突变点A，尽管随着时间的推移，实时监测数据的增多，滤波估计的精度越来越高。卡尔曼滤波值将以曲线II的趋势逐渐稳定并收敛于真实值。但在收敛的过程中对突变点之后的退化状态无法进行快速跟踪，会出现状态估计预测误差Δx，影响实时剩余寿命的预测和系统维护维修决策的制定。

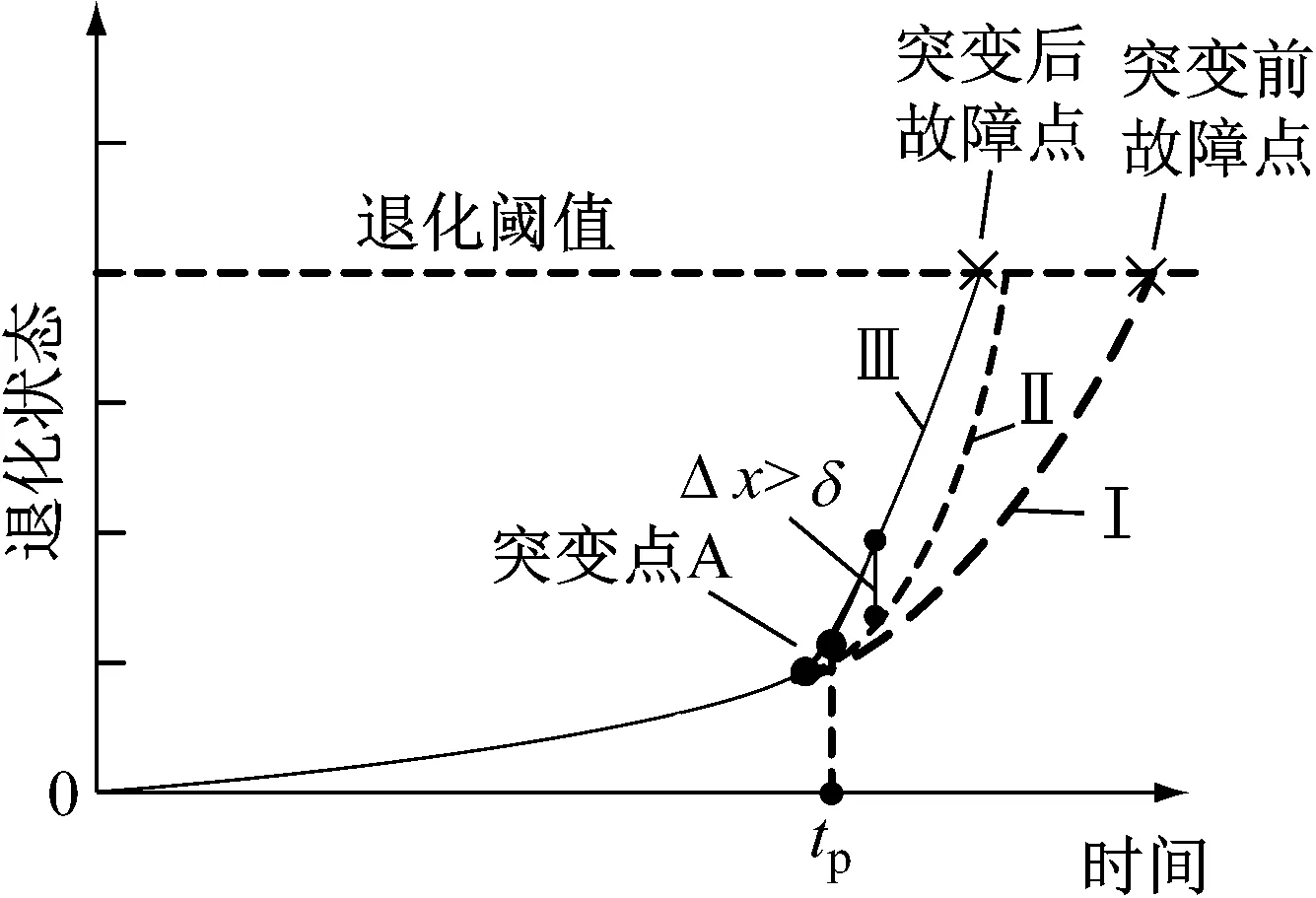
图6 退化状态预测模型修正示意图

由以上分析可知采用卡尔曼滤波对系统进行状态估计及预测时，当系统出现状态突变点后，仍然存在以下问题：

(2)在正常的卡尔曼滤波递推过程中，由于初始值的准确值不能确切知道，通常选取都是不准确的，只能假定一初值。当滤波时间充分长后，它的卡尔曼最优滤波值将渐近稳定而不依赖于滤波初值的选择，但初始值选择误差大，其收敛于真值的速度慢。系统退化状态出现突变点后，初始值选择不准确会增加状态估计与预测过程中的误差。

(3)在卡尔曼滤波递推过程中，开始的几步递推计算中得到的状态估计值十分粗略，这一阶段称为粗估阶段。在卡尔曼滤波粗估阶段，Kt的值和滤波估计误差Pt很大，可以对状态预测进行较好的修正；之后进入精估阶段，Kt和Pt的值逐渐减小，使得观测值对状态估计值的修正作用变小。

因此，采用状态空间模型进行状态估计与预测时，在突变状态之后对状态空间模型进行修正，期望观测信息对状态估计值产生较强的修正作用，使得状态估计较快地收敛于部件退化的真实状态。可以更好的对突变状态进行跟踪，减少预测误差，提高收敛速度和预测精度。需对模型进行以下修正：

(1)状态估计时增加突变点后的监测信息，修正系统模型参数，进行自适应的状态估计。

(2)利用突变点提供的信息在突变点后进行系统模型参数修正的同时，重新选择滤波初始值。使得状态预测值较快的接近被估计的真实状态。

(3)在突变点修正滤波增益Kt，通过大的滤波增益Kt可以对状态估计进行较强的修正。

5.1期望最大化参数估计

当系统在运行过程中，随着外界环境的变化，模型参数可能发生变化，因此可以利用监测数据对模型参数进行估计。设式(4)和式(5)中的未知参数可用一个参数向量θ表示，即θ={Ftt-1,Ht,Qt,Rt}，在可实时监测条件下，需进行状态空间模型参数的估计及退化状态的预测。

期望最大化(Expectation-Maximization，EM)算法主要用来计算基于不完全数据的极大似然估计，尤其适用于估计存在隐藏变量下的状态空间模型参数估计。因此首先采用期望最大化算法从初始时刻以迭代的方式实时估计状态空间模型参数。该算法包括两个步骤：E步骤和M步骤。

(1)E步骤

θ0={F0,H0,Q0,R0}

(9)

为使退化状态初值选择更为合理，本文采用卡尔曼前向滤波及固定区间反向滤波相结合的方法在参数估计的同时来选取最优的退化状态初值。

已知在ti+n时刻，接收到i+n个监测点的监测信息，求得其对数最大似然函数为：

(10)

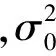
(11)

采用期望最大化算法估计参数，需首先计算式的期望值，记为EXY,θk[lnL(θ)]。

(12)

卡尔曼光滑算法即为求期望值的过程[21]，首先求得：

(13)

(14)

(15)

(16)

(17)

(18)

将式(13)～式(18)代入式(12)，可求得：

(19)

(2)M步骤

通过求解最大似然估计算法求得各参数的估计值：

(20)

EM算法不断进行E步骤和M步骤的迭代，直到似然函数值稳定不再变化，即求解到ti+n时刻的参数估计值θti+n。

5.2突变点后初始值的修正

θti+n={Fti+nti+n-1,Hti+n,Qti+n,Rti+n}

(21)

如图6所示，当在ti+n时刻检测到ti时刻存在突变点A，需修正突变点A之后的卡尔曼滤波模型初始值及参数。

利用ti时刻及之前接收到的所有监测信息采用EM参数估计算法求得的参数估计值记为：

θti={Ftiti-1,Hti,Qti,Rti}

(22)

(23)

式中：β与γ为参数修正因子，且β+γ=1。选择γ<β，通过参数修正因子来加大突变点之后的数据的权重，相应减少突变点之前的数据的权重，重新选择突变点之后参数估计初值。

(24)

5.3滤波增益的修正

检测到突变点后，通过自适应增益函数增加突变点后的增益矩阵Kt的模值，使得状态估计比较快的收敛于部件退化的真实状态。假设检测到ti处退化状态发生突变，构造一自适应增益函数gi(ti)为：

(25)

式中：a与b为自适应增益函数的参数，增大滤波增益的方法是以牺牲滤波的最优性为代价的，因此并非滤波增益收敛到1的速度越大越好，因此自适应增益函数的参数a与b的选择应同时考虑其收敛速度与滤波最优性的问题。

(26)

5.4退化状态突变后自适应滤波

(27)

(28)

(29)

(30)

(31)

(32)

式中ti时刻需修正卡尔曼滤波增益，修正后的卡尔曼滤波增益记为：

(33)

6 试验结果

6.1振动信号的特征提取

齿轮箱中的齿轮发生故障时，安装在轴承位置的传感器经过轴和轴承接收到振动信号，信号衰减最小，可以很好地反映齿轮箱的振动特性。因此在进行寿命预测时选择齿轮疲劳试验中离断齿位置最近，且在轴承座位置布置的4#传感器输出的463组振动信号进行特征提取。试验中采样频率25.6 kHz，采样时间60 s，采样间隔9 min，将采样点次数折算为监测时间，就可得到如图7所示的4#传感器输出的特征值随监测时间变化曲线图。该曲线包含了从开始磨合阶段到完成疲劳试验共77 h的振动信号均方幅值。

整个RMS曲线在去除个别奇异点后整体变化趋势可反映试验齿轮各监测点磨损情况与振动能量对应的关系。整个RMS曲线在开始啮和阶段逐渐趋于稳定，在60 h后齿轮磨损增大，幅值显著上升直到发生断齿。

图7 4#传感器特征值提取RMS曲线

(1) 当监测时间t∈[0,10]时，齿轮处于啮合阶段，RMS呈下降趋势，表明齿轮在开始啮合阶段均方幅值比正常疲劳磨损要大。

(2)t∈[10,68]时，RMS值在逐渐增加，表明齿轮啮合后齿面进入正常磨损阶段。由于电压值不稳定，导致转速发生变化在大约30 h处和55 h处RMS突然增大，然后RMS又趋于稳定。

(3)t∈[68,77]时，RMS急剧增大，从最后齿轮疲劳失效后结果得知，此时的齿轮磨损开始加剧，直到在77.2 h处发生断齿，此时退化状态故障阈值为xf=77.375 mm/s2。

6.2状态空间建模及突变状态检测

6.2.1 状态空间建模及初始参数的选择

根据式(13)和(14)建立齿轮疲劳试验中4#传感器输出的观测值与系统状态之间状态空间模型为：

x(t)=Ftt-1x(t-1)+w(t-1)

(34)

y(t)=Htx(t)+v(t)

(35)

6.2.2 退化状态突变点的检测

系统开始运行经过齿轮啮合阶段进入齿轮正常退化阶段后进行突变点检测，选择误警率η=0.25%，平均运行链长ARL=400，取最小的预警退化量为Δμ=20，退化均值μ0=51.952，方差σ2=3.044，突变预警阈值由式和式可求解突变检测预警阈值h=59.702 3，得到累积和统计量如图8所示。

图8 报警时CUSUM统计量变化图

图8中A点为突变点，B点为预警点。检测到退化状态的突变点发生在在66.3 h处，在69 h处累积和统计量超过预警阈值h进行报警，由于齿轮磨损退化状态发生变化。

6.3预测模型的修正

根据检测到的突变点对寿命预测的模型进行修正可以更好的跟踪系统的动态变化，为剩余寿命的实时预测及维护维修策略的制定提供依据。因此利用检测出的66.3 h处突变点提供的退化信息对预测模型进行修正，在69 h处开始预测其退化值与实际接收到的齿轮退化值进行比较，计算其预测误差。

6.3.1 突变点后初始值的修正

图9 预测模型修正前后所估计的参数F的取值

Fig.9 Values of the estimated parameters for modified prediction model comparison with original

由图9可知突变点前，状态空间模型修正前后的模型参数F取值变化较接近，在突变点处，根据突变点信息对模型进行修正后的参数变化较大，而模型修正前的参数变化相对滞后。

6.3.2 滤波增益参数的选择

由图10可知随着ti的增大，b为定值时，增大参数a的值，或在a为定值时，减小b的取值，gi(ti)收敛到1的速度在增大，(增大滤波增益的方法是以牺牲滤波的最优性为代价的，因此并非gi(ti)收敛到1的速度越大越好，因此自适应增益函数的参数a与b的选择应同时考虑其收敛速度与滤波最优性的问题。本文中滤波增益参数取值为a=8×10-2，b=2时，则自适应增益函数gi(ti)，如图11所示。

(a) kti=1时，改变参数a的自适应增益函数取值

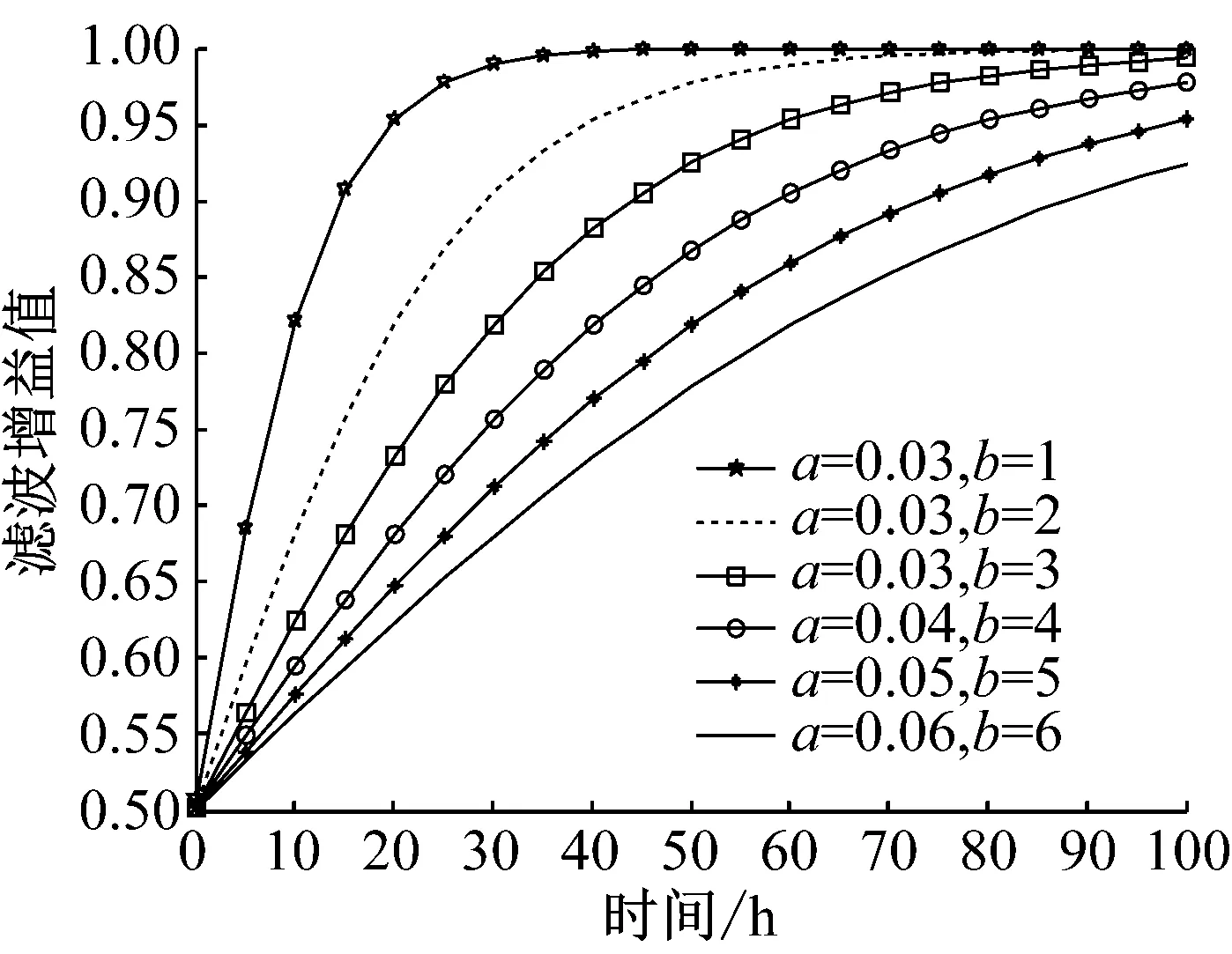
(b) kti=1时，改变参数b的自适应增益函数取值

图11 参数为a=0.08，b=2的自适应增益函数

6.4剩余寿命预测

利用修正后的状态空间方程可对系统的监测点之后的退化状态进行预测，通过预测到的退化状态值及已知的退化状态故障阈值可求解首次到达故障阈值的时间(First Passage Time, FPT)[9]。进而以蒙特卡洛的分析方法求得在tp时刻所预测的系统的平均剩余寿命uN(tp)为：

(36)

式中：Tfm为第m次预测退化状态到达利用齿轮疲劳试验所得系统故障阈值xf=77.375 mm/s2的时间，N为蒙特卡洛仿真次数，用最小方差控制N的取值，即N满足：

(37)

试验中ε的取值为：ε=e-10。

图12给出在69 h处状态空间模型修正前后通过预测得到齿轮磨损退化状态均值。

(a) 状态空间模型未修正时预测退化状态

(b) 状态空间模型修正后预测退化状态

如图13所示可知在不同时刻修正前后的状态空间模型所预测的退化状态曲线均不同，69 h处预测状态值偏离实际值较多，误差较大。随着监测信息增多，滤波时间充分长后，修正前后的状态空间模型所预测的退化状态均接近真实值，误差减小。在相同的预测时刻，比较修正前后的状态空间模型预测结果，修正后的状态空间模型所预测的齿轮退化状态更接近真实值，能很好地预测系统退化状态发生突变后其退化状态的变化以及故障发生时间。未修正的状态空间模型所预测到的特征不能很好地突变后的退化状态变化，预测剩余寿命误差较大。由图13(e)可以看到在刚检测到突变状态点时，由于修正后的状态空间模型刚刚修正初值，开始的递推计算所得到的状态估计值比较粗略，估计误差较大，但经过几步递推运算之后状态估计值比较快的靠近被估计的真实状态，能够很好地跟踪其动态变化。

(a) 69 h处模型修正前后预测

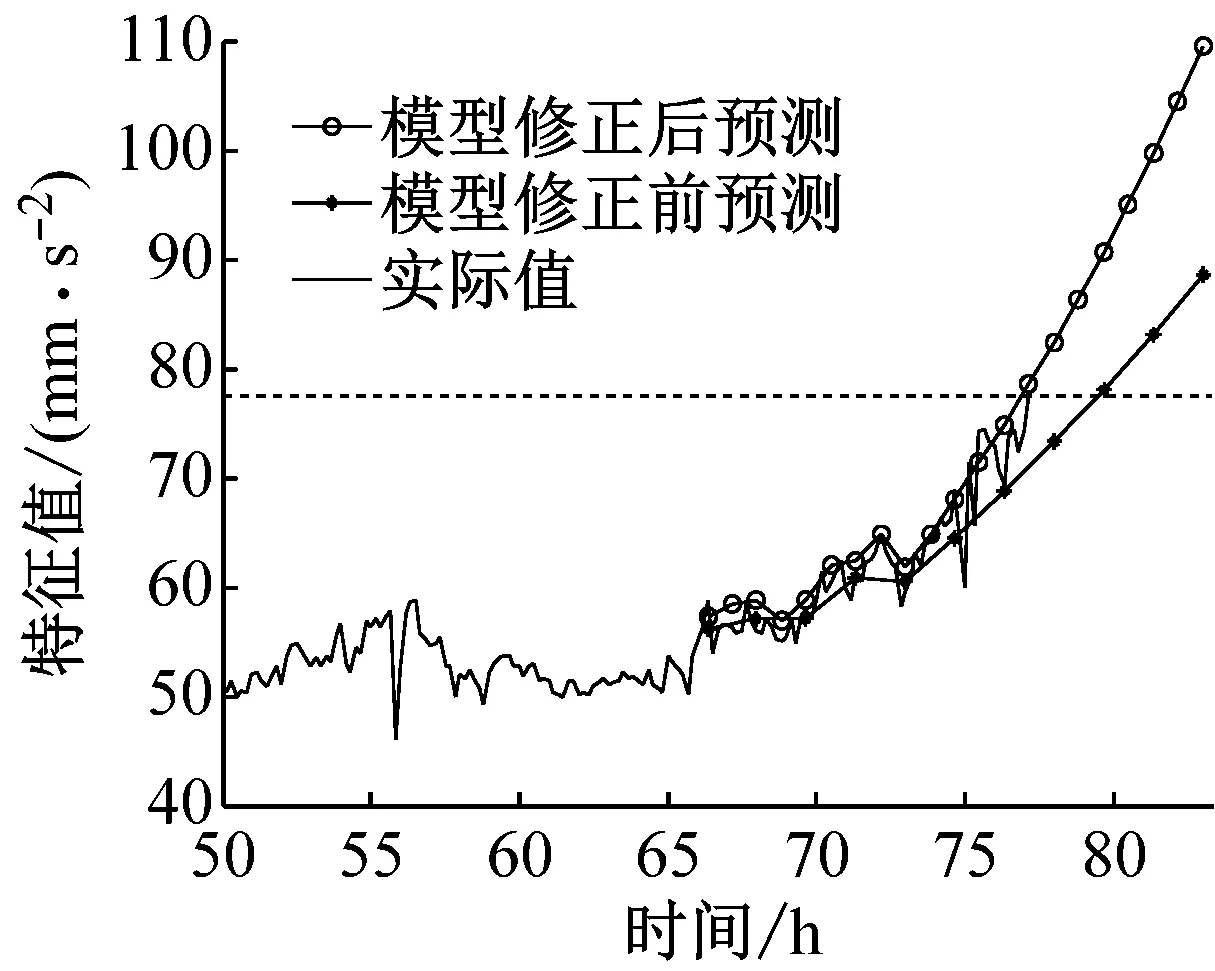
(c) 73 h处模型修正前后预测

(d) 75 h处模型修正前后预测

(e) 76 h状态空间模型修正前后处

(f) 73 h处模型修正前后预测

由蒙特卡罗法求得状态空间模型修正前后不同时刻所预测的剩余寿命概率密度函数如图14所示。可知在同一预测时刻，状态空间模型修正后所预测的平均剩余寿命更接近真实的剩余寿命，且其概率密度函数与修正前的状态空间模型所预测的剩余寿命概率密度函数相比预测方差减小。随着预测时间的推移，接收到监测信息的增加，在76 h利用状态空间模型所预测到的剩余寿命概率密度函数，模型修正前后剩余寿命概率密度函数峰值均逐渐接近真实值。

为进一步比较状态空间模型修正前后预测剩余寿命的准确性，引入预测准确度的概念[23]。预测准确度PA为：

(38)

式中：‖表示绝对值；uN(tp)表示tp时刻预测求得的平均剩余寿命；Ta为齿轮实际剩余寿命；T*=77.2为齿轮实际故障时间，则Ta=T*-tp。由此可计算状态空间模型修正前后其预测准确度的比较如表1所示。

如表1所示，随着监测信息的增多，修正前后的状态空间模型所预测剩余寿命预测误差均是逐渐减小，预测准确度逐渐提高。但在不同的预测点69 h、70 h以及73 h和75 h处相比，状态空间模型修正后所预测的剩余寿命准确度均高于利用修正前的状态空间模型所预测求得的预测准确度。在76 h处未修正预测模型剩余寿命逐渐接近模型修正后所预测到的剩余寿命，为进一步说明考虑突变状态检测的齿轮实时剩余寿命预测有效性，建立基于反向传播(Back Propagation，BP)神经网络齿轮寿命预测模型并与本文所提预测方法进行比较。首先将齿轮疲劳试验中突变点之后的退化状态特征值作为网络训练输入向量；然后建立三层BP神经网络并对网络进行训练；最后利用训练好的网络得到当前时刻退化状态的预测曲线。

仍以齿轮疲劳寿命试验4#传感器输出的463组振动信号进行特征提取，通过仿真算例将预测值和实际值相比较(如图15所示)可知：在不同的预测点70 h、 73 h、75 h和76 h处相比，随着训练数据增加，神经网络预测退化状态所预测剩余寿命预测误差逐渐减小。如图15(d)所示在76 h处通过神经网络预测模型所预测的齿轮故障时间为80.1 h，基于状态空间模型突变点修正后所预测的齿轮故障时间为77 h，齿轮实际故障时间T*=77.2 h。可知在相同的预测点，基于状态空间模型突变点修正后所预测的剩余寿命准确度高于利用BP神经网络所预测求得的预测准确度。

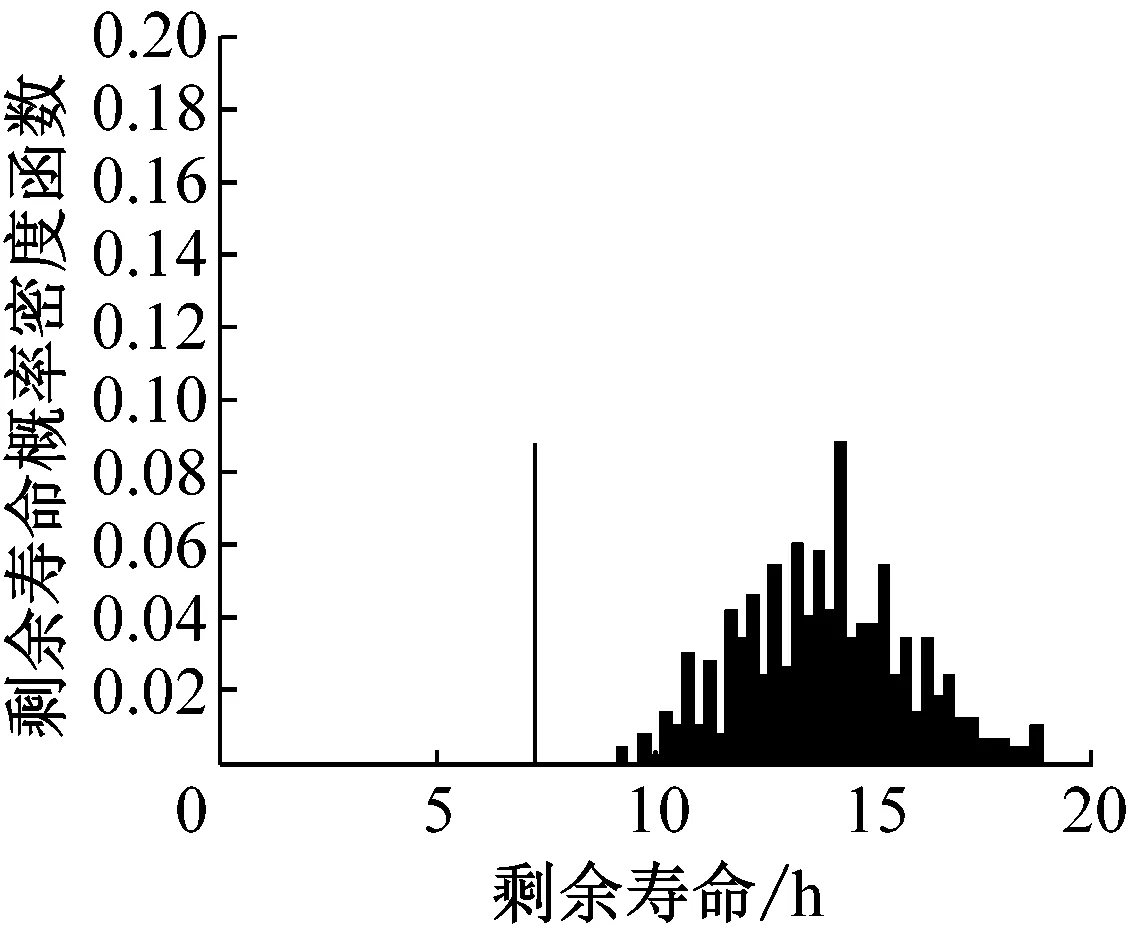
(a) 70 h修正前剩余寿命概率密度函数

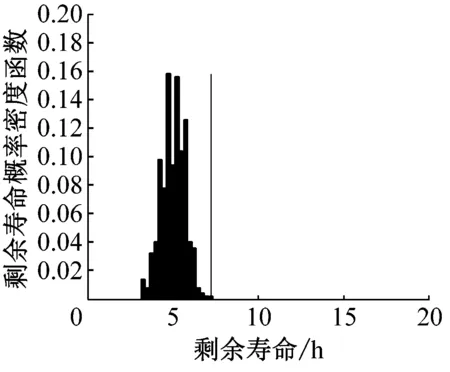
(b) 70 h修正后剩余寿命概率密度函数

(c) 73 h修正前剩余寿命概率密度函数

(d) 73 h修正后剩余寿命概率密度函数

(e)75 h修正前剩余寿命概率密度函数

(f)75 h修正后剩余寿命概率密度函数

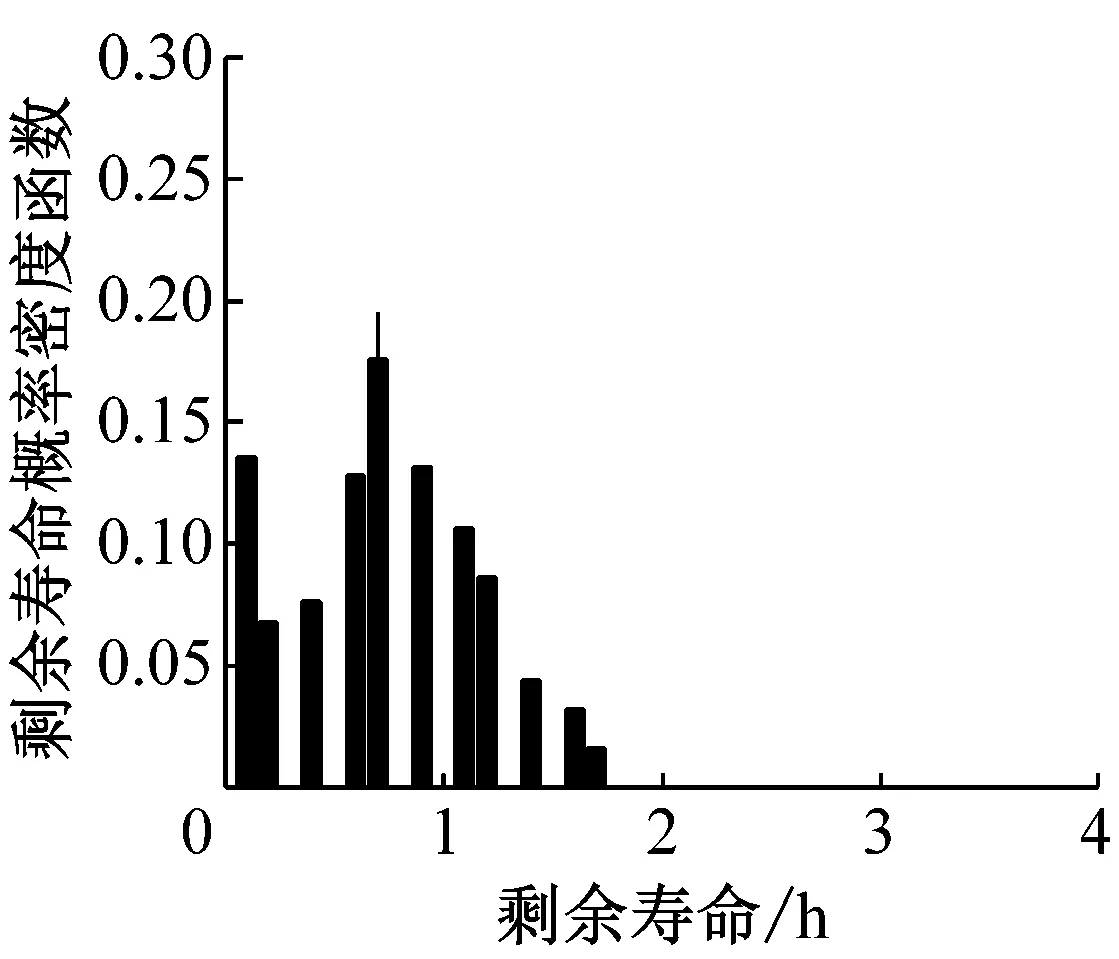
(g) 76 h修正前剩余寿命概率密度函数

(h) 76 h修正后剩余寿命概率密度函数

预测时刻tp/h修正前uN(tp)/h修正后uN(tp)/h实际剩余寿命Ta/h修正前预测准确度PA/%修正后预测准确度PA′/%6914．15．78．228．9569．517012．35．07．229．1769．44736．54．04．245．2495．24751．32．32．259．0995．45761．01．01．295．2495．24

由此可知当接收到的监测信息足够多时，利用数据驱动的剩余寿命预测方法可以较准确地预测剩余寿命。但是基于状态的预防性维护维修更关心系统整个运行过程中的实时剩余寿命预测的准确度，尤其系统退化性能发生突变后准确的剩余寿命预测可以为及时调整预防性维护维修策略提供必要的依据。因此本文所提基于状态空间的齿轮实时剩余寿命预测方法，在系统运行过程中发生突变后，利用突变点所提供的信息对模型进行修正可以更好地跟踪系统的退化状态的变化，提高系统运行过程中实时剩余寿命的预测准确度。

7 结 论

本文根据接收到的齿轮实时监测信息建立系统状态空间预测模型。同时考虑异常点检测与剩余寿命预测的关联性，对齿轮磨损退化过程中的突变状态点进行检测后，利用退化状态突变点所提供的寿命信息采用卡尔曼前向滤波及平滑算法结合EM参数估计算法在滤波的同时修正状态空间模型，进行状态估计及寿命预测。将退化状态突变点检测和剩余寿命的预测进行联合研究，通过齿轮疲劳寿命试验验证其修正后的预测模型可以更快的对系统的动态变化进行跟踪，提高实时剩余寿命预测准确度。

(a) 70 h处神经网络预测退化状态

(b) 73 h处神经网络预测退化状态

(c) 75 h处神经网络预测退化状态

(d) 76 h处神经网络预测退化状态

作者的下一步工作是针对齿轮利用多个传感器接收到的数据，考虑数据融合并对预测模型修正，进行更为准确的实时寿命预测。

[1] 冯志鹏, 秦嗣峰. 基于 Hilbert 振动分解和高阶能量算子的行星齿轮箱故障诊断研究[J]. 振动与冲击, 2016, 35(5): 47-54.

FENG Zhipeng,QIN Sifeng. Planetary gearbox fault diagnosis based on Hilbert vibration decomposition and higher order differential energy operator[J]. Journal of Vibration and Shock, 2016, 35(5): 47-54.

[2] SI X, WANG W, CHEN M, et al. A degradation path-dependent approach for remaining useful life estimation with an exact and closed-form solution[J]. European Journal of Operational Research, 2013, 226(1): 53-66.

[4] 孙强, 岳继光. 基于不确定性的故障预测方法综述[J]. 控制与决策, 2014, 29(5): 769-778.

SUN Qiang, YUE Jiguang. Review on fault prognostic methods based on uncertainty[J]. Control and Decision, 2014, 29(5): 769-778.

[6] CARR M J, WANG W. An approximate algorithm for prognostic modelling using condition monitoring information[J]. European Journal of Operational Research, 2011, 211(1): 90-96.

[7] SUN J, ZUO H, WANG W, et al. Application of a state space modeling technique to system prognostics based on a health index for condition-based maintenance[J]. Mechanical Systems and Signal Processing, 2012, 28: 585-596.

[8] BRESSEL M, HILAIRET M, HISSEL D. Extended kalman filter for prognostic of proton exchange membrane fuel cell[J]. Applied Energy, 2016, 164: 220-227.

[9] TANG D, MAKIS V, JAFARI L, et al. Optimal maintenance policy and residual life estimation for a slowly degrading system subject to condition monitoring[J]. Reliability Engineering & System Safety, 2015, 134: 198-207.

[10] LALL P, LOWE R, GOEBEL K. Extended kalman filter models and resistance spectroscopy for prognostication and health monitoring of leadfree electronics under vibration[J]. Reliability, IEEE Transactions on, 2012, 61(4): 858-871.

[11] WANG W. A model to predict the residual life of rolling element bearings given monitored condition information to date[J]. IMA Journal of Management Mathematics, 2002, 13(1): 3-16.

[12] 胡昌华, 王志远, 周志杰. 基于随机滤波理论的剩余寿命预测方法研究[J]. 系统仿真技术, 2011, 7(2): 83-88.

HU Changhua, WANG Zhiyuan, ZHOU Zhijie. A study on residual life prediction method based on stochastic filtering theory[J]. System Simulation Technology, 2011, 7(2):83-88.

[13] 李鑫, 吕琛, 王自力, 等. 考虑退化模式动态转移的健康状态自适应预测[J]. 自动化学报, 2014, 40(9): 1889-1895.

LI Xin, LÜ Chen, WANG Zili, et al. Self-adaptive health condition prediction considering dynamic transfer of degradation mode[J]. Acta Automatica Sinica, 2014, 40(9):1889-1895.

[14] 周东华, 魏慕恒, 司小胜. 工业过程异常检测, 寿命预测与维修决策的研究进展[J]. 自动化学报, 2013, 39(6): 711-722.

ZHOU Donghua, WEI Muheng, SI Xiaosheng. A survey on anomaly detection, life prediction and maintenance decision for industrial processes[J]. Acta Automatica Sinica, 2013, 39(6): 711-722.

[15] SON J, ZHANG Y, SANKAVARAM C, et al. RUL prediction for individual units based on condition monitoring signals with a change point[J]. Reliability, IEEE Transactions on, 2015, 64(1): 182-196.

[16] 刘亚琼, 王铁, 武志斐, 等. QC商用车变速器疲劳试验振动分析[J]. 机械传动, 2014, 38(7): 104-105.

LIU Yaqiong, WANG Tie, WU Zhifei, et al. Vibration analysis of QC commercial vehicle transmission fatigue test[J]. Mechanical Drive, 2014, 7(38): 104-105.

[17] HINES J A, MARK M D. Bending-fatigue damage-detection on notched-tooth spiral-bevel gears using the average-log-ratio, ALR, algorithm[J]. Mechanical Systems and Signal Processing, 2014, 43(1): 44-56.

[18] UNNIKRISHNAN J A, VEERAVALLI V V, MEYN S P. Minimax robust quickest change detection[J]. Information Theory, IEEE Transactions on, 2011, 57(3): 1604-1614.

[19] 伊廷华, 郭庆, 李宏男. 基于控制图的 GPS 异常监测数据检验方法研究[J]. 工程力学, 2013, 30(8): 133-141.

YI Tinghua, GUO Qing, LI Hongnan. The research on detection methods of gps abnormal monitoring data based on control chart[J].Engineering Mechanics, 2013,30(8):133-141.

[20] SIEGMUND D. Error probabilities and average sample number of the sequential probability ratio test[J]. Journal of the Royal Statistical Society. Series B (Methodological), 1975: 394-401.

[21] WANG W, CARR M, XU W, et al. A model for residual life prediction based on Brownian motion with an adaptive drift[J]. Microelectronics Reliability, 2011, 51(2): 285-293.

[22] KHAN M E, DUTT D N. An expectation-maximization algorithm based kalman smoother approach for event-related desynchronization (ERD) estimation from EEG[J]. Biomedical Engineering, IEEE Transactions on, 2007, 54(7): 1191-1198.

[23] LU C, TAO L, FAN H. An intelligent approach to machine component health prognostics by utilizing only truncated histories[J]. Mechanical Systems and Signal Processing, 2014, 42(1): 300-313.

Modelfortherealtimeremainingusefullifepredictionofgearsbasedontheabruptchangedetection

SHIHui1,ZENGJianchao1,2

(1.Division of Industrial and System Engineering, Taiyuan University of Science and Technology, Taiyuan 030024，China; 2. School of Computer Science and Control Engineering, North University of China, Taiyuan 030051, China)

In order to accurately predict the gear remaining useful life in the degradation process, a new method for the real-time prediction of gear contact fatigue remaining useful life was put forward, which is a method integrating the abrupt change detection and remaining life prediction. A state-space model for predicting degradation states of gear wear was established by using the real time monitoring vibration information to update the model parameters. The Kalman forward filtering and smoothing algorithm combined with the parameter estimation by the expectation-maximization algorithm was made in use and the prediction model was modified incessantly to change the filtering effect according to the life information from the abrupt change detection. The real-time monitoring data of the contact fatigue life collected on a gear test rig were used to verify the model proposed. The results show that a revised prediction model using the abrupt point information can achieve the prediction faster than a dynamic tracking system, and can improve the accuracy of gear degradation state and real-time remaining useful life prediction.

remaining useful life prediction; state-space models; Kalman filtering; abrupt change detection; model correction

TH163.5；TP277

A

10.13465/j.cnki.jvs.2017.21.026

2016-01-11 修改稿收到日期：2016-08-05

石慧 女，博士，副教授，1979年生

曾建潮 男，教授，博士生导师，1963年生