耦合内流动力学的海洋柔性立管振动控制
2017-11-30赵志甲邬依林
郭 芳, 刘 屿, 赵志甲, 罗 飞, 邬依林
(1.华南理工大学 自动化科学与工程学院,广州 510641;2. 广东第二师范学院计算机科学系,广州 510310)
耦合内流动力学的海洋柔性立管振动控制
郭 芳1, 刘 屿1, 赵志甲1, 罗 飞1, 邬依林2
(1.华南理工大学 自动化科学与工程学院,广州 510641;2. 广东第二师范学院计算机科学系,广州 510310)
针对耦合时变内流和洋流动力学的海洋柔性立管系统,为有效抑制其振动和避免控制溢出问题,基于立管原始无限维模型,将边界控制技术与高增益观测器相结合,设计了边界控制器对立管振动进行主动控制,通过严格的数学分析,验证了控制作用下立管系统的稳定性和闭环系统状态的一致有界性。仿真结果验证了所设计边界控制算法对立管振动抑制的有效性。
海洋立管;边界控制;Lyapunov理论;高增益观测器
海洋柔性立管的振动控制问题经常发生在海洋工程中,然而过度的振动将会制约立管系统的生产性能并导致立管疲劳破损,带来经济损失。因此,开展立管系统的振动主动控制研究,为提高生产效率和保障海洋生产安全提供了可能。
近年来,为避免因截断模型法产生的控制溢出问题,国内外学者运用边界控制、鲁棒控制以及自适应控制等,在原始的无限维立管模型基础上直接对其开展控制设计,已取得一定成果。然而,目前国外研究成果[1-6]都没有考虑到内流动力学对立管系统的影响。在国内,作者已有研究成果[7-10]把内流动力学纳入立管系统动力学模型,并设计了PD控制、鲁棒控制、自适应控制、二维控制等,均能达到抑制立管振动的控制目的,同时也验证了内流动力学的影响将降低立管振动的自然频率。然而,在以上文献中,均假定所提出控制律中的状态信号均可通过传感器测量得到或后向差分计算得到。在实际工程中,测量噪声将随着差分计算过程被放大,这将影响以上文献中所设计控制器的有效执行。因此,在本文中将边界控制技术与高增益观测器相结合,设计边界控制器对立管振动进行控制,从而避免了因后向差分计算带来的噪声影响。
本文以耦合内流动力学的海洋柔性立管为研究对象,在原始的无限维立管模型基础上直接对其开展控制设计,将Lyapunov直接法、边界控制技术、高增益观测器相结合,设计边界振动控制算法,从而达到抑制立管振动的目的。随后基于所设计的控制算法,通过严格的数学分析验证控制作用下系统的稳定性。最后对所设计控制算法的有效性进行了数值仿真。
1 立管系统动力学模型
图1给出了一类典型的海洋柔性立管系统。控制器U(L,t)作用在立管顶端,且方向向右,并用以减少立管振动偏移量w(x,t)。
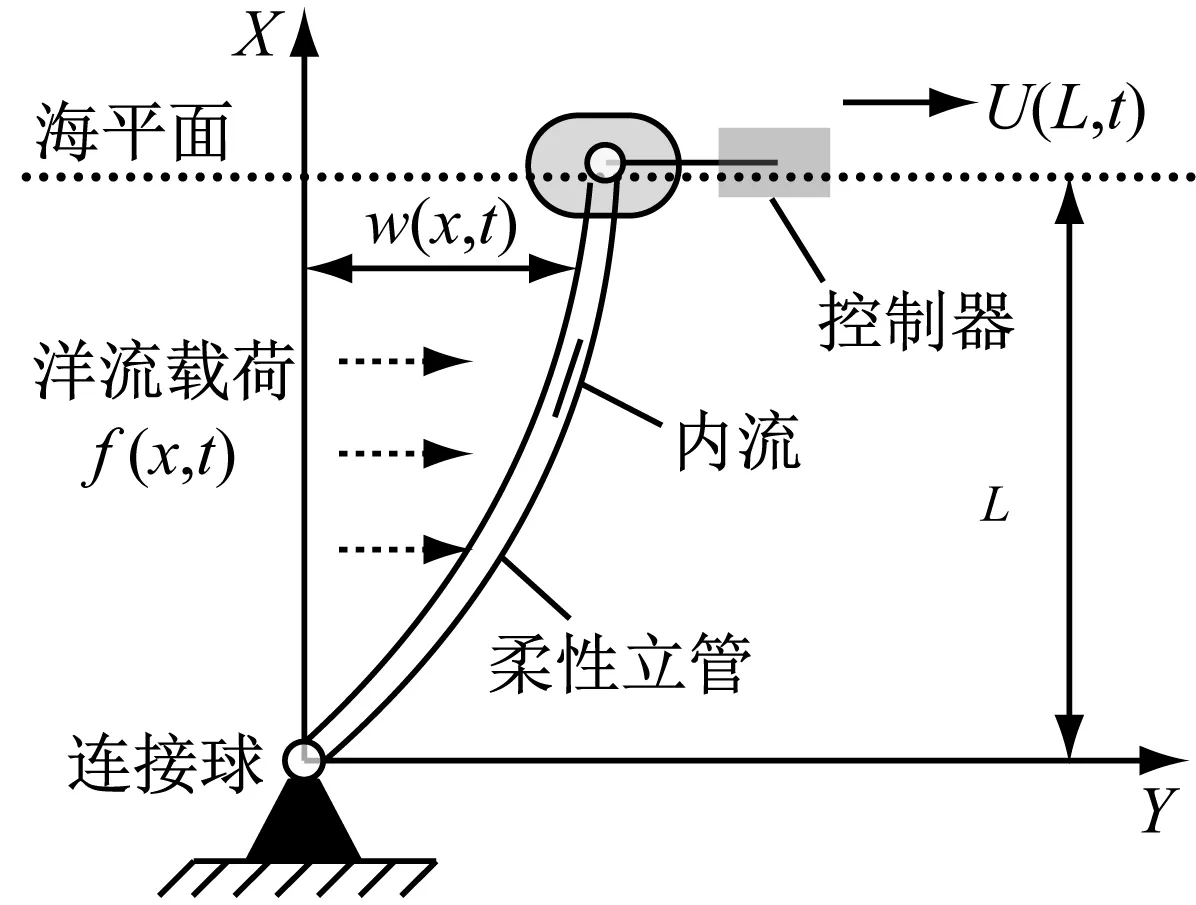
图1 典型的海洋柔性立管系统
本文研究在Liu已有成果的基础上开展,因此,式(9)~(11)可直接得到本文所研究立管系统的模型,其中控制方程为

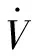
(1)
∀(x,t)∈(0,L)×[0, +∞),边界条件为
(2)
∀t∈[0, +∞),初始条件为

(3)
∀x∈(0,L)。

2 控制设计
本文的控制目标是在系统状态不可精确获得的条件下,在立管顶端设计边界控制用以抑制柔性立管的振动。本节将Lyapunov直接法、边界控制技术、高增益观测器相结合,设计边界控制器,用以抑制立管振动。其后,通过严格的数学分析,验证控制作用下立管系统的稳定性。
2.1预备知识
引理1对θ1(x,t),θ2(x,t)∈R,σ>0,∀(x,t)∈[0,L]×[0, +∞),有[11-13]
(4)
引理2对θ(x,t)∈R,∀(x,t)∈[0,L]×[0,+∞),若满足
θ(0,t)=0, ∀t∈[0,+∞)
(5)
有
(6)
2.2边界控制
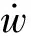
引理3[14]假设系统的输出y(t)以及对应的n阶微分是有界的,且有|y(k)|
(7)
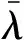
(8)
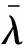
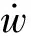
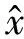
(9)
其中定义π2的动力学和x2(t)的误差为
(10)
为对立管系统式(1)~(3)的振动进行主动控制,本文给出如下边界控制律
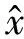
(11)
其中k1,k2,k3>0是控制增益。
选取Lyapunov候选函数为
V(t)=Va(t)+Vb(t)+Vc(t)
(12)
其中能量项Va(t)为
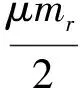
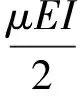
(13)
交叉项Vb(t)为

(14)
附加项Vc(t)为

(15)
其中α,μ>0。
引理4Lyapunov候选函数式(12)是正定的,且具有如下上下界
0≤ϑ1[Va(t)+Vc(t)]≤V(t)≤
ϑ2[Va(t)+Vc(t)]
(16)
式中,ϑ>01,ϑ2>0。
应用不等式(4)~(6),由式(14)可得
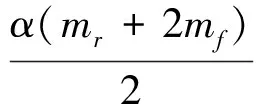


(17)
式中:
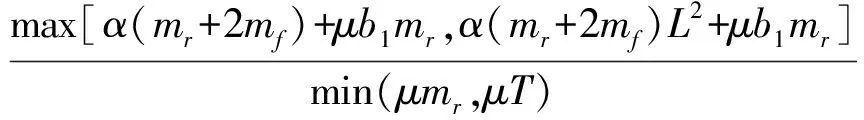
式(17)可改写为
-γVa(t)≤Vb(t)≤γVa(t)
(18)
选取γ使得
γ1=1-γ>0,γ2=1+γ>1
(19)
将式(19)代入到式(18)得
0<γ1Va(t)≤Va(t)+Vb(t)≤γ2Va(t)
(20)
结合式(12)与式(20)可得
0≤ϑ1[Va(t)+Vc(t)]≤V(t)≤
ϑ2[Va(t)+Vc(t)]
(21)
式中,ϑ1=min(γ1, 1) >0,ϑ2=max(γ2, 1) >0。
引理5Lyapunov候选函数(12)的时间导数具有如下上界
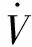
(22)
式中,ϑ,ω>0。
对式(12)求导得
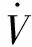
(23)
对式(13)求导并代入式(1),并分部积分可得
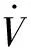
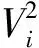
(24)
式中,δ1>0。
对式(14)求导并代入式(1),应用分部积分再结合式(2)和引理1可得
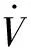
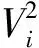
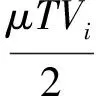
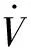
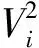

(25)
式中,δ2,δ3,δ4>0。
对式(15)求导可得
(μk3+αk1+3αmfVi)x1(t)x2(t)
(26)
将式(24)~(26)和控制律式(11)代入式(23),再结合引理1可得
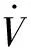
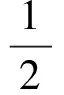
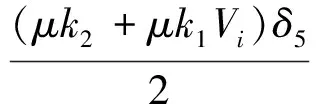
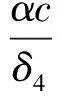

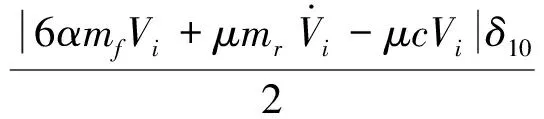

(27)
式中,δ5~δ10为任意正常数。结合式(19)的第一式,选择适当的k1~k3,α,μ,δ1~δ10满足以下条件:
γ<1,
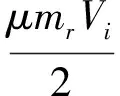
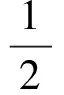
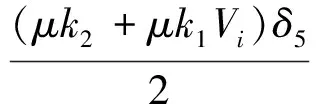
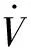

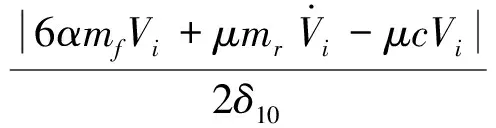
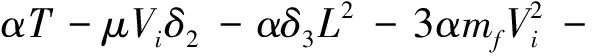
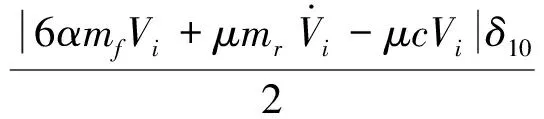
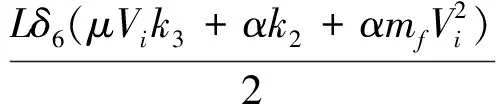
(28)
将式(28)代入式(27)可得
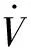

-ϑ3[Va(t)+Vc(t)]+ω
(29)
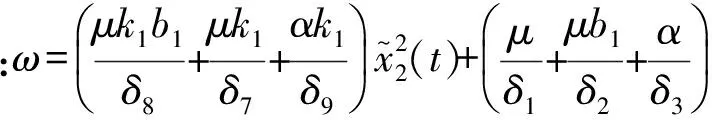
结合不等式(29)和式(16),可得
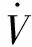
(30)
式中,ϑ=(ϑ3/ϑ2)。
2.3稳定性分析
定理1对式(1)~(3)所描述的柔性立管系统,在假设1和边界控制器式(11)作用下,有
1) 一致有界:w(x,t)一致包含于紧集Ω1中
Ω1:={w(x,t)∈R‖w(x,t)≤χ1,
∀(x,t)∈[0,L]×[0,+∞)}
(31)
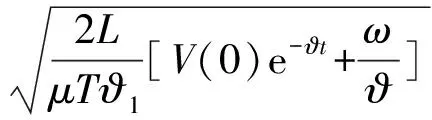
2) 一致最终有界:w(x,t)最终收敛于紧集Ω2中
∀x∈[0,L]}
(32)

式(22)乘以eϑt有
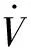
(33)
对式(33)进行积分运算可得

(34)
式(34)表明V(t)是有界的。
由式(6)、式(13)以及式(16)可得
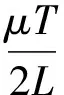
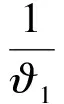
(35)
结合式(34)~(35)有
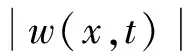
(36)
∀(x,t)∈[0,L]×[0, +∞)。进一步可得

(37)
∀x∈[0,L]。
3 数值仿真
本节将采用有限差分法[15-18]对柔性立管系统在海洋洋流扰动作用下的振动控制情况进行仿真研究,以便于对所提出边界控制(11)的有效性进行验证。立管系统的详细参数如表1所示。
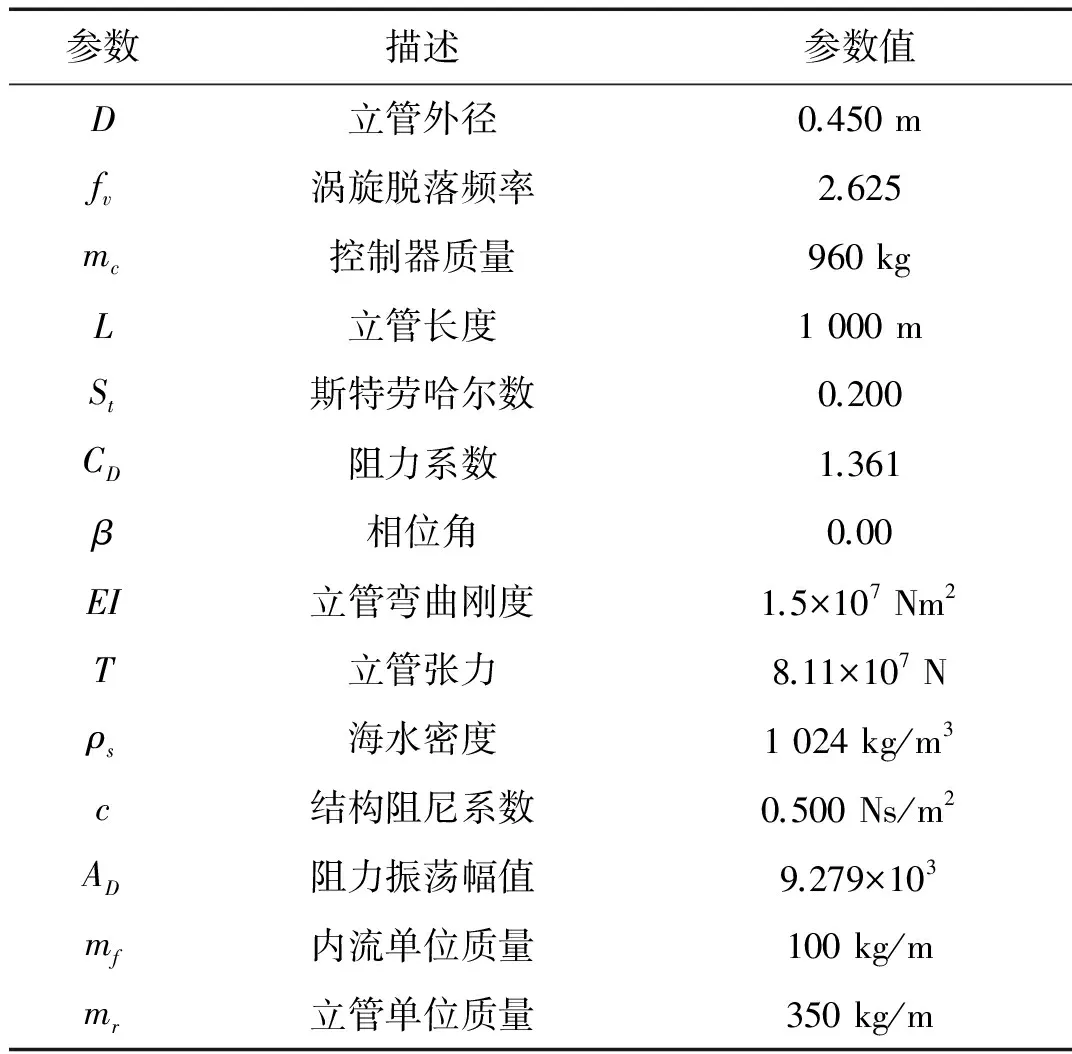
表1 柔性立管系统参数
洋流干扰载荷f(x,t)可表示为
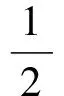
(38)
式中:ρs为海水密度,D为立管外径,β为相位角,AD(即AD(x,t))和CD(即CD(x,t))分别为阻力的振荡部分幅值和系数,Vs(即Vs(x,t))为时变海流流速,fv=StVs/D为涡旋脱落频率,其中St为斯特劳哈尔数。
海洋洋流速度与深度关系为[19]
(39)
其中Vo(L,t)为海洋表面洋流流速为
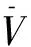
(40)
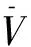
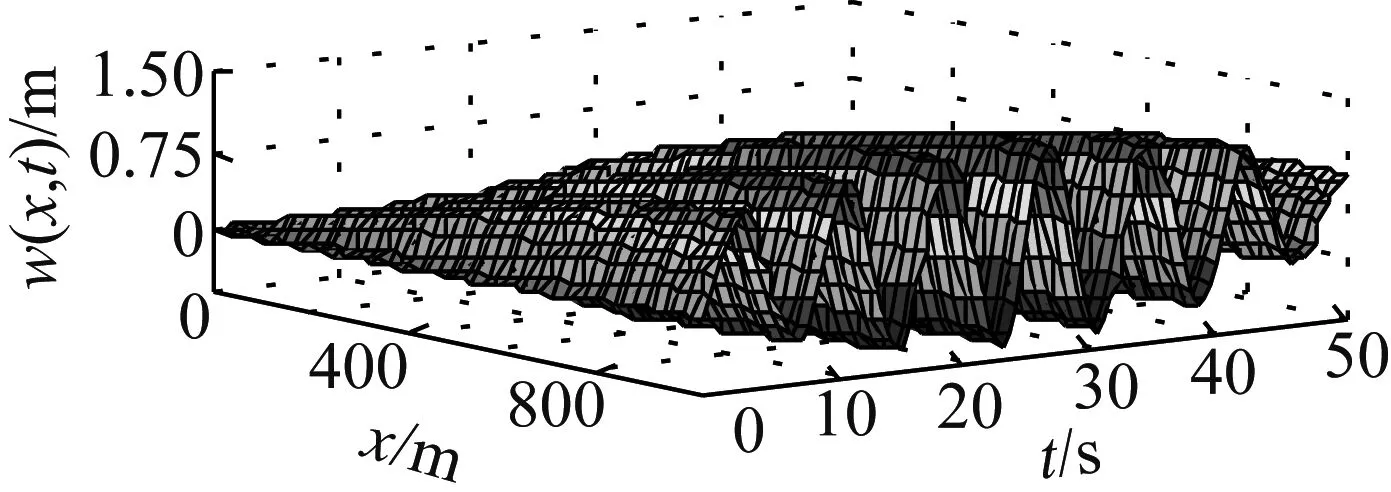
Vi(t)=0.5+0.2cos(0.867t)
(41)
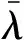
(a) 无控制

(b) 有控制

(a) 无控制

(b) 有控制
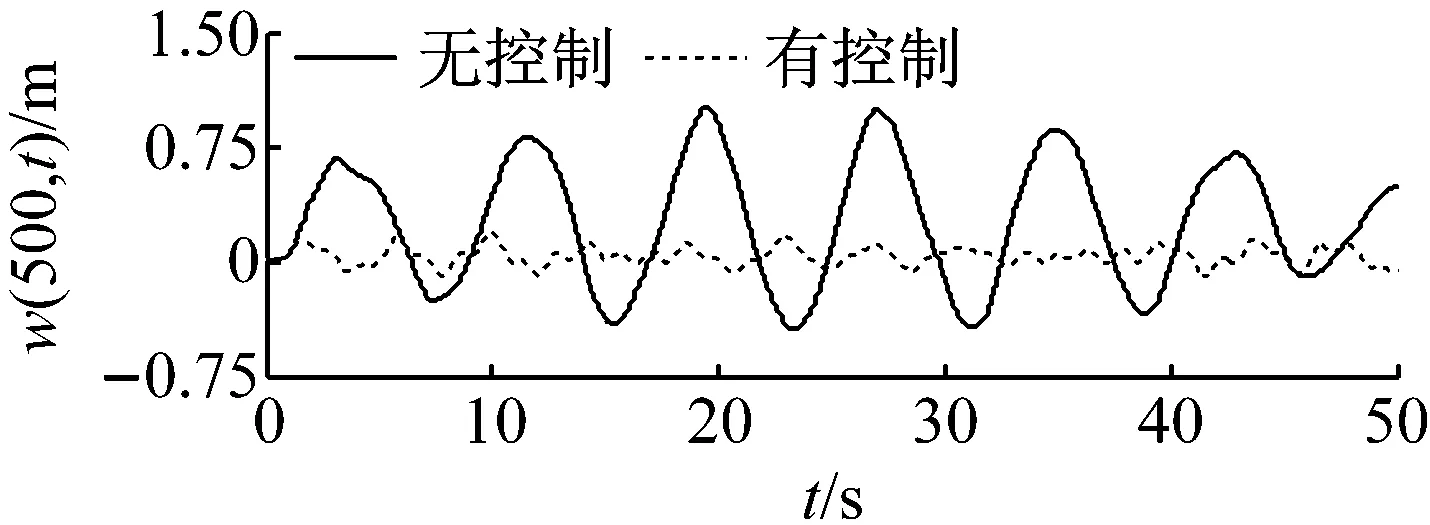
(a) x=500 m
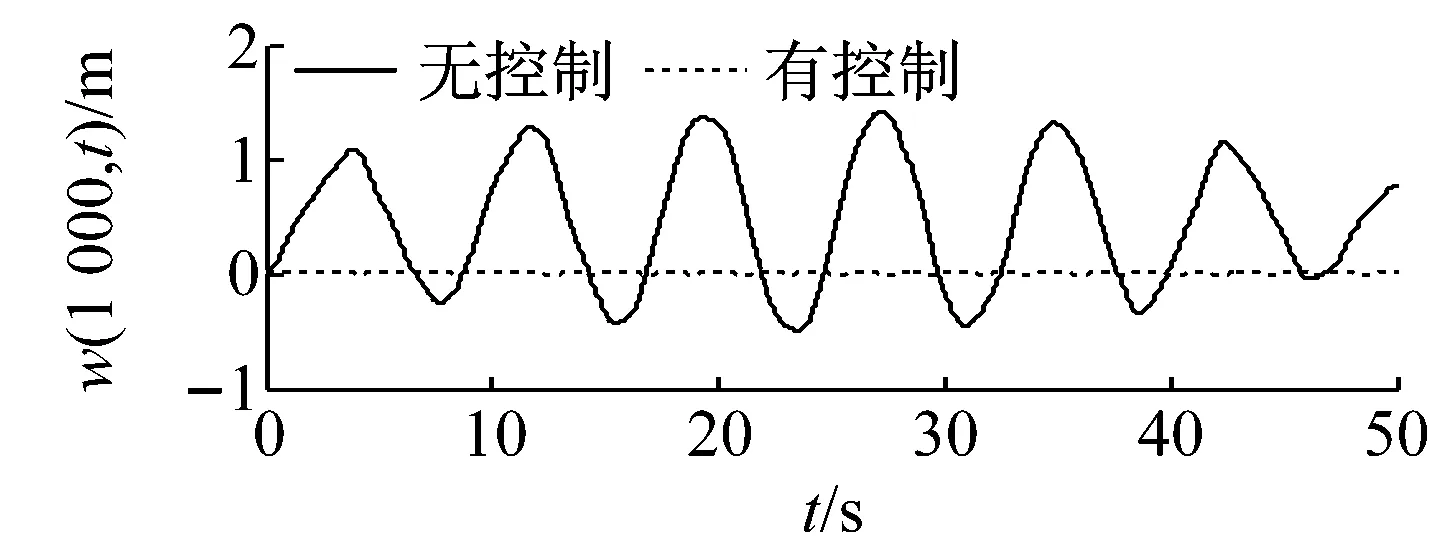
(b) x=1 000 m

(a) x=500 m
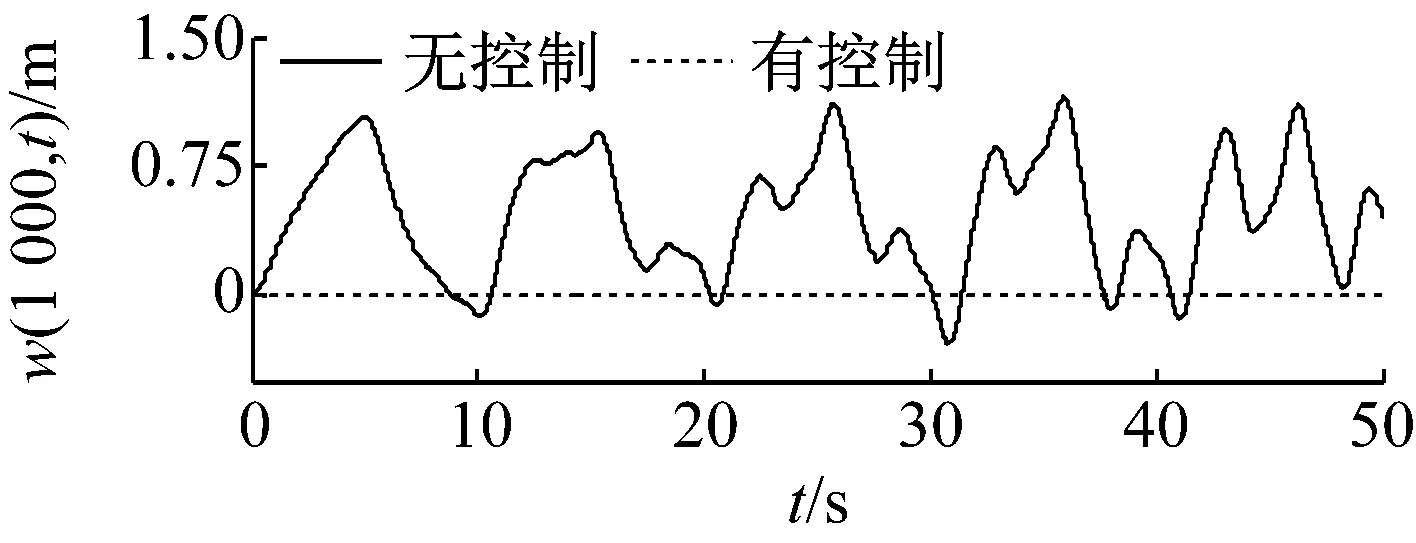
(b) x=1 000 m
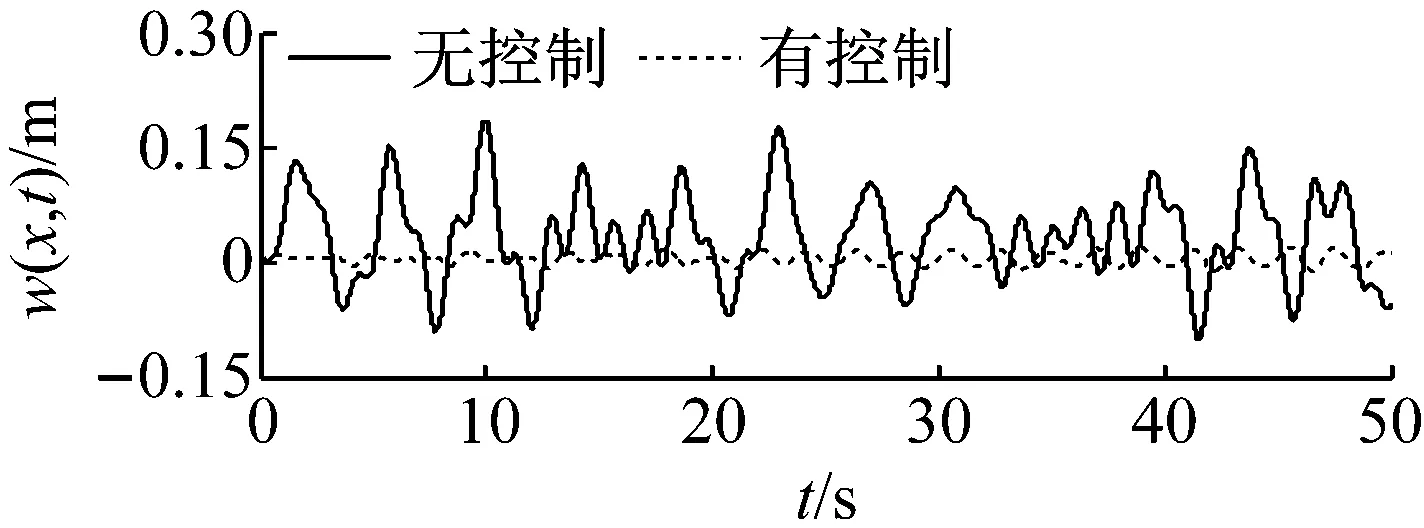
(a) 无内流

(b) 有内流
由仿真结果图2~7可得如下结论:
1)由图2~6可知,立管系统在所设计控制器式(11)作用下,无论有无内流,其振动偏移量都得到了显著减小,说明了在系统状态不可精确获得的条件下,本文所提控制算法仍具有很好的控制效果。
2)对比图2~3和图4~5,当考虑内流动力学后,立管振动情况发生了显著的变化,即内流对立管系统振动有很大影响,它直接减小立管振动的自然频率。
3)由图4~6可知,虽然在立管中部(x=500 m)并未布置执行器,但所设计边界控制算法同样具有非常好的控制效果。
4)由图7可知,控制输入的范围为:-8×104N~1×105N,其中负数控制输入用来抵消外部环境干扰。
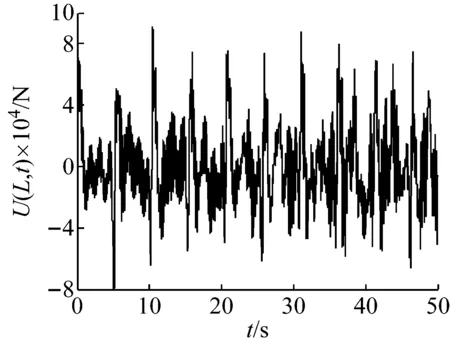
图7 边界控制输入
4 结 论
本文以耦合内流动力学的海洋柔性立管的振动控制问题为研究对象。首先,在原始的无限维立管模型基础上,将边界控制技术与高增益观测器相结合,设计边界控制策略对立管振动进行控制。其后运用Lyapunov综合法,通过严格的数学分析验证控制作用下系统的稳定性。此控制器设计不需知道扰动量的精确模型,因此对系统参数的变化具有稳定鲁棒性。最后,仿真结果验证了所设计边界控制器能有效地抑制立管的振动。
[1] GE S S, HE W, HOW B V E, et al. Boundary control of a coupled nonlinear flexible marine riser[J]. IEEE Transactions on Control Systems Technology, 2010, 18(5): 1080-1091.
[2] HE W, GE S S, HOW B V, et al. Robust adaptive boundary control of a flexible marine riser with vessel dynamics[J]. Automatica, 2011, 47(4): 722-732.
[3] HOW B V E, GE S S, CHOO Y S. Active control of flexible marine risers[J]. Journal of Sound and Vibration, 2009, 320(4/5): 758-776.
[4] DO K D, PAN J. Boundary control of transverse motion of marine risers with actuator dynamics[J]. Journal of Sound and Vibration, 2008, 318(4/5): 768-791.
[5] DO K D, PAN J. Boundary control of three-dimensional inextensible marine risers[J]. Journal of Sound and Vibration, 2009, 327(3/5): 299-321.
[6] NGUYEN T L, DO K D, PAN J. Boundary control of two-dimensional marine risers with bending couplings[J]. Journal of Sound Vibration, 2013, 332(16): 3605-3622.
[7] 邬依林,刘屿,吴忻生. 基于时变内流的柔性立管自适应边界控制[J]. 控制理论与应用,2013,30(5):618-624.
WU Yilin, LIU Yu, WU Xinsheng. Adaptive boundary control of a flexible riser coupled with time-varying internal fluid[J]. Journal of Control Theory & Applications, 2013, 30(5): 618-624.
[8] 高红霞,赵志甲,吴忻生,等. 基于内流动力学的海洋输油柔性立管鲁棒边界控制[J]. 控制理论与应用,2012,28(6):785-791.
GAO Hongxia, ZHAO Zhijia, WU Xinsheng, et al. Robust boundary control for flexible fluid-transporting marine riser based on internal fluid dynamics[J]. Journal of Control Theory & Applications, 2012, 28(6): 785-791.
[9] LIU Y, HUANG H W, GAO H X, et al. Modeling and boundary control of a flexible marine riser coupled with internal fluid dynamics[J]. Journal of Control Theory & Applications, 2013, 11(2): 316-323.
[10] 吴忻生,李林野,刘屿,等. 海洋输油立管的建模及边界控制[J]. 华南理工大学学报(自然科学版),2012,40(8):32-38.
WU Xinsheng, LI Linye, LIU Yu, et al. Modeling and boundary control of a marine riser[J]. Journal of South China University of Technology (Natural Science Edition), 2012, 40(8): 32-38.
[11] 刘屿,翁轩,吴忻生,等. 大加减速轴向移动系统的振动控制[J]. 振动工程学报,2014,27(6):878-884.
LIU Yu, WENG Xuan, WU Xinsheng, et al. Vibration control of an axially moving system with high ac-/deceleration[J]. Journal of Vibration Engineering, 2014, 27(6): 878-884.
[12] 刘屿,邬依林,赵志甲. 大加减速轴向移动系统鲁棒边界控制[J]. 控制与决策,2014,29(10):1771-1776.
LIU Yu, WU Yilin, ZHAO Zhijia. Robust boundary control of an axially moving system with high ac-deceleration[J]. Control and Decision, 2014, 29(10): 1771-1776.
[13] HE W, GE S S. Robust adaptive boundary control of a vibrating string under unknown time-varying disturbance[J]. IEEE Transactions on Control Systems Technology, 2012, 20(1): 48-58.
[14] BEHTASH S. Robust output tracking for nonlinear system[J]. International Journal of Control, 1990, 51: 1381-1407.
[15] HE W, SUN C, GE S S. Top tension control of a flexible marine riser by using integral-barrier Lyapunov function[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(2): 497-505.
[16] HE W, ZHANG S, GE S S. Adaptive control of a flexible crane system with the boundary output constraint[J]. IEEE Transactions on Industrial Electronics, 2014, 61(8): 4126-4133.
[17] HE W, GE S S. Vibration control of a flexible beam with output constraint[J]. IEEE Transactions on Industrial Electronics, 2015, 62(8): 5023-5030.
[18] HE W, ZHANG S, Ge S S. Robust adaptive control of a thruster assisted position mooring system[J]. Automatica, 2014, 50(7): 1843-1851.
[19] FENG S Z, LI F Q, LI S J. Introduction to marine science[M]. Beijing: Higher Education Press, 1999.
Vibrationcontrolofaflexiblemarinerisercoupledwiththeinternalfluiddynamics
GUOFang1,LIUYu1,ZHAOZhijia1,LUOFei1,WUYilin2
(1. School of Automation Science and Technology, South China University of Technology, Guangzhou 510641, China; 2. Department of Computer Science, Guangdong University of Education, Guangzhou 510310, China)
To suppress the riser’s vibration and avoid the control spillover, based on the original infinite-dimensional model of a flexible marine riser structure dynamically coupled with the time-varying internal fluid and ocean current, a boundary control was developed for the vibration reduction by applying the boundary control technique and high-gain observers. The stability of the control system and uniform boundedness of the closed-loop signals were strictly demonstrated by using the Lyapunov theory. The effectiveness of the proposed boundary control scheme was illustrated by some simulation results.
marine risers; boundary control; Lyapunov theory; high-gain observer
TP273
A
10.13465/j.cnki.jvs.2017.21.024
国家自然科学基金(61203060);广东省科技计划(2016A010106007);华南理工大学中央高校基本科研业务费(2017ZD058)
2016-03-30 修改稿收到日期:2016-09-08
郭芳 女,博士生,1992年8月生
刘屿 男,副研究员,硕士生导师,1977年12月生
