改进K-SVD算法在曲轴轴承AE信号的去噪研究

张峻宁， 张培林， 华春蓉， 秦 萍

(1.军械工程学院七系，石家庄 050003; 2.西南交通大学 机械工程学院，成都 610031)

改进K-SVD算法在曲轴轴承AE信号的去噪研究

张峻宁1， 张培林1， 华春蓉2， 秦 萍2

(1.军械工程学院七系，石家庄 050003; 2.西南交通大学 机械工程学院，成都 610031)

针对柴油机曲轴轴承声发射(Acoustic Emission, AE)信号中裂纹特征信息微弱，易与噪声混淆等问题，在K-SVD字典对信号稀疏的基础上，提出一种均值信号改进的K-SVD字典的滑动轴承AE信号去噪算法。重组均值信号和扩展到K-SVD信号矩阵中，在实现K-SVD稀疏AE信号矩阵的同时，稀疏提取均值信号的裂纹信号，利用K-SVD处理前、后的均值信号提取其中的本底信号，并采用模糊加权均值滤波器对本底信号进行去噪，去除与裂纹信号混淆的噪声，最后根据信号矩阵、稀疏的裂纹信号和去噪后的本底信号得到低信噪比的AE信号。试验结果表明，所提算法有效去除了AE信号中易与裂纹信号混淆的噪声，使故障特征更加明显，成功刻画了滑动轴承不同摩擦状态间的变化。

滑动轴承；声发射；K-SVD；均值信号

在所有的内燃机零件中，曲轴轴承由于巨大的机械负荷，强烈的冲击干扰，以及恶劣的工作环境，成为监测最困难的部件之一。近几年，不少学者通过声发射技术(Acoustic Emission, AE)监测该轴承状态[1-2]，但AE信号噪声污染严重，易与信号的摩擦声、裂纹声[3]混淆，造成滑动轴承状态监测效果不佳。因此，为了消除噪声和提高轴承故障诊断的质量，针对AE信号的降噪技术在现实生活中有很重要的意义。

目前常用的AE信号去噪方法均是通过频率分布差异去除噪声，认为噪声能量集中于高频，信号的有用信息分布于有限频率区间，如易太连等[4]利用信息与噪声在小波变换的极大值点变化的不同性质做曲轴信号的去噪处理，吴定海等[5]利用双树复小波包和自适应块阈值对柴油机缸盖振动信号降噪，但是这些方法均是依靠基函数和阈值的选取，一旦选择不当，去噪时很容易丢失高频信号中的有用信息，最终造成信号失真，而字典学习不需要先验获取信号和噪声的统计特性，通过有用信息与噪声不同的稀疏性分离噪声，避免了传统频域降噪方法易去除高频故障特征信息的缺陷，如Elad等[6]提出的K-SVD字典，很好的分离了图像边缘高频信息和噪声。而后，发展了如基于聚类的局部字典学习算法(clustering-based denoising with locally lerrned dictionary,K-LLD)[7]，最小二乘字典学习算法(Least Squares Dictionary Learning Algorithm, LS-DLA)[8]等，针对图像降噪都取得了良好的效果，但直接应用到AE信号降噪效果不佳。

基于此，本文以噪声污染严重的滑动轴承信号为研究对象，改进K-SVD中的均值信号，提高K-SVD对AE一维信号的降噪能力。首先，通过重组矩阵策略将均值信号嵌入到K-SVD训练矩阵中，实现稀疏信号矩阵的同时提取均值信号中的裂纹信号，然后利用K-SVD前、后的均值信号得到本底信号，并通过模糊加权均值滤波器滤除本底信号中的噪声，最后将上述信号叠加，组成降噪信号。仿真和实验表明，该算法能够较好的消除裂纹信号中的噪声和保留磨损故障的特征信息。

1 K-SVD字典及均值信号的重要性

1.1信号的K-SVD字典算法

信号K-SVD降噪定义为：

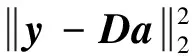
(1)

具体步骤如下：

(1)字典算法相关参数的定义：m为字典的大小，t为迭代的次数，γ为拉格朗日惩罚算子，G为噪声增益，w为滑动窗口尺寸，再初始化冗余字(DCT矩阵)；

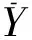
(2)

式中：ciY为Y信号中第i个列向量；cijY为矩阵中i向量的第j个元素；biY为第i列向量信号的均值标准化。

(3)系数编码：运用正交匹配追踪算法(Orthonormal Matching Pursuit, OMP)[9]，求解每一块列向量biY的稀疏编码向量ai：ai=OMP(Di,biY,ζ,T)；

(4)字典更新：逐步更新字典原子di；

① 提取di原子稀疏表示的信号子集，计算与信号Y的残差：

Λp=〈i|1≤i≤M,[p,i]≠0〉

(3)

② SVD分解：

(4)

③ 更新原子：

(5)

④ 根据设定的迭代次数更新原子

(5)信号去噪：利用更新的字典稀疏信号矩阵CY′，并对其均值逆标准化见式(6)，最后按照步骤(2)中逆序规则恢复信号y′。

CY′=CY′+M

(6)

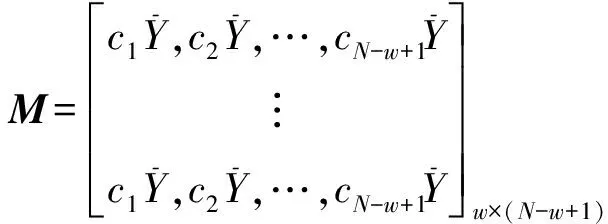
易见，K-SVD算法中均值标准化，实质是对信号Y均值滤波，提高了SVD分解的可靠性，但步骤5中未处理均值信号M，直接将M与信号矩阵CY′相加，则造成了裂纹信号中的噪声残留问题，具体分析见1.2节所示。

1.2均值信号对K-SVD降噪的重要性

K-SVD中的均值信号实质是均值滤波器滤波后的信号，K-SVD中的信号均值标准化等效于式(7)[10]。

(7)

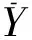
图1 K-SVD中的均值标准化

但实际中噪声为标准高斯白噪声的情况很少，而且均值滤波器滤波对滑动窗口尺寸要求苛刻。针对采样率较高的AE信号，只有经较大滑动窗口滤波的信号，标准的高斯白噪声才会被消除[11]，而实际中，为了充分稀疏K-SVD的信号矩阵，常会将滑动窗口w设定为较小的尺寸，达不到消除高斯白噪声的尺寸。因此，K-SVD中的均值信号降噪困难，受到了滑动窗尺寸的制约。

为了验证本文想法，建立仿真滑动轴承摩擦故障时的AE信号如图2所示。

x(t)=s1(t)+s2(t)+e(t)+zs

(8)

式中：s1(t)=2×e-50×t×sin(2π×64×t)，仿真轴与瓦间因接触摩擦产生的幅值大的瞬时弹性波型的摩擦信号；s2(t)=0.6×e-100×t×sin(2π×91×t)，仿真轴承因磨损脱落激发的幅值较小的AE裂纹信号；e(t)=0.05×sin(2π×10t)+sin(2π×5t)为本底信号；zs的0.1 dB高斯噪声，采样频率为50 kHz。

图2 噪声污染下的AE信号仿真

首先计算仿真信号在不同尺寸滑动窗口w下的K-SVD的信号降噪效果，见图6的K-SVD降噪曲线所示。可以发现，只有在w=20(较小)的滑动窗下的K-SVD的信号矩阵被充分稀疏，信号的信噪比越高，验证了K-SVD信号矩阵稀疏的要求。再比较不同大小滑动窗口下的K-SVD的均值信号降噪图，如图3所示。易见，无论是在K-SVD信号降噪效果较好的滑动窗，还是尺寸较小或较大的滑动窗，K-SVD均值信号中噪声均有残留和信号失真现象。由此说明，经K-SVD字典降噪的信号中遗留的噪声，是来自于K-SVD的均值信号。基于此，本文提出对K-SVD的均值信号算法改进。

(a) w=5

(b) w=20

(c) w=100

2 K-SVD字典的均值信号改进

2.1均值信号的K-SVD同步提取

为了解决K-SVD的均值信号降噪和K-SVD信号矩阵稀疏问题，本文依据字典仅对信号敏感的特性，试图将均值信号中的摩擦、裂纹信号与噪声分离，提出对K-SVD算法中均值信号的K-SVD稀疏策略；为了不再增加K-SVD的计算负担，减小运算时间，通过均值信号分段重组并嵌入到原信号矩阵中，实现信号矩阵和均值信号同时稀疏的效果，最终达到提取均值信号中摩擦、裂纹信号以及分离噪声的目的，具体步骤如下。

(2)均值信号M分段重组规则：按照上述方法划分列向量，并将全部列向量组成均值信号矩阵CM，易见，标尺移动的次数t=ceil[(G-w)/l]，ceil(x)表示取大于x的最小整数，均值信号M∈RG；

2.2基于模糊加权均值滤波的均值信号降噪

文献[12]运用模糊加权的思想，提出了基于模糊隶属度的加权均值滤波器，较好实现了混合噪声的抑制。本文均值信号经K-SVD提取后，仅剩下本底信号和残余的噪声，与文献[12]情况类似，故基于模糊加权均值滤波器对高斯、脉冲噪声的敏感性，利用模糊加权均值滤波器对本底信号降噪：

针对滑动窗，对每个样本建立隶属度，定义隶属度函数见式(9)所示。为了抑制脉冲噪声的影响，设定其对应隶属度较低，并认定当隶属度函数加权均值后得到信号为原信号时，是滤波器最佳输出估计。因此通过迭代的方式不断更新隶属度函数，以无限逼近最佳状态。

(9)

式中：di=xi-y，xi为滑动窗(滑动窗大小为w)内样本值，y为滤波输出；Ψ为尺度参数，依据经验选取Ψ=5 000。

(1)设定滑动窗内信号的均值y0为滤波初次输出信号，依据式(9)计算滑动窗各样本信号的隶属度。

(2)由(1)得到的隶属度di，再计算输出信号y1，比较y1、y0的差值是否小于阈值ε，若小于，则退出迭代，否则设定y1为新y0，利用式(9)计算新隶属和输出信号y1，直到y1-y0≤ε，退出循环。

2.3本文算法步骤与框架图

本文首次提出对K-SVD中的均值信号板块降噪处理，下面给出本文算法框架图和具体步骤。

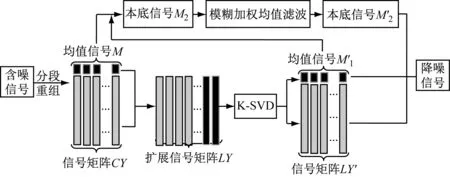
图4 本文算法框架图

3 仿真试验与分析

为了验证K-SVD改进算法的有效性，以式(8)滑动轴承仿真信号为例，主要做了两方面研究。

(1)分析和讨论均值信号在K-SVD中同步稀疏的意义，以及模糊加权均值滤波器对混合降噪的作用。随机设定本文字典参数(m=100，w=10，l=1)，对仿真信号降噪。图5是本文算法的均值信号效果图。对比图5(a)、(b)，可见均值信号的K-SVD同步稀疏策略，能够提取原均值信号中的摩擦、裂纹信号，避免了混合噪声的干扰。图5(c)验证了模糊加权均值滤波器对本底信号降噪的有效性。图5(d)是最终均值信号图，对比图(a)，易见均值信号不仅降噪效果明显，同时能够较好保留含有故障特征信息的摩擦、裂纹信号，验证了本文对K-SVD均值信号所做工作的有效性。

(a) K-SVD的均值信号

(b) 均值信号的K-SVD同步稀疏

(c) 模糊加权均值滤波器对本底信号的降噪

(d) 均值信号改进后的效果

同时，比较了不同w时的信号降噪规律见图6所示。由图中曲线可知，本文算法和K-SVD算法均会随w的增大而信噪比降低，但是相比K-SVD，本文算法降噪更彻底，尤其在滑动窗口较小时，降噪提高大约6 dB，很好解决了均值信号降噪和信号矩阵稀疏性的问题。

图6 不同w时的仿真信号降噪效果

(2)比较本文算法与常用算法的降噪效果，见表1所示。易见，在不同程度污染的高斯白噪声中，本文算法的降噪效果较好，尤其在原信号被噪声严重污染时，经本文算法降噪后信号信噪比明显高于其他降噪算法，证明了该算法在滑动轴承AE信号降噪的优势。

表1 不同降噪方法的信号信噪比

4 应用实例

对滑动轴承摩擦故障实验中的声发射数据降噪。该数据来源于西南交通大学摩擦试验台的S195-2型柴油机，声发射传感器安置于柴油机输出端主轴承座附近的机体壁上，模拟实验工况2 000 r/min，工率4.67 kW，采样频率为100 kHz。

图7 判断滑动轴承摩擦状态的实验电路

实验通过切断滑动轴承轴与瓦之间润滑油路，模拟滑动轴承接触摩擦故障。图7为实验故障监测电路图，分析上图可知，当滑动轴承处于润滑状态时，油膜电阻R1呈电阻无穷大，此时电路不通，灯泡不亮；当切断润滑油路后，电阻R1会随轴与瓦的接触摩擦不断增强而逐渐减小，此时灯泡逐渐变亮，电路电流逐渐增大。此外测量了滑动轴承背面温度，作为滑动轴承是否出现故障的依据，并规定切断油路为“0”，断油前为“负”时刻，断油后为“正”时刻，具体工况见表2。

表2 切断润滑前后滑动轴承特征的变化

图8是滑动轴承信号降噪前后的对比图。可以发现，在频域图中降噪前的信号，突出频域频带很广，噪声范围很宽，通过本文算法降噪的信号，图中频谱更加集中，部分频段噪声得到了抑制，且在时域图中局部特征更加清晰。

滑动轴承发生摩擦故障时，小波包频带能量会发生变化，因此采用小波包频带能量特征来对比滑动轴承声发射信号的降噪效果。首先通过3层小波包变换提取频带能量特征，再利用LS-SVM分类器对滑动轴承摩擦故障状态监测。具体参数为：选取轴承不同程度摩擦故障(正常润滑、边界摩擦，严重摩擦)的样本150个，其中正常润滑样本50个，边界润滑样本50个，严重润滑50个。选取前20个作为训练样本，剩下的作为测试样本。具体诊断结果见表3所示。

由表3可见，直接采用原始信号提取的特征，监测滑动轴承的摩擦故障效果不佳，表明原始信号中噪声与故障信号混叠严重，降低了轴承的摩擦故障监测精度；EMD是一种非平稳信号分析方法，通过将信号从高频到低频分解降噪，但是滑动轴承噪声和故障信号频域混叠，因此EMD降噪效果一般；小波软阈值是将信号转换到小波域，通过判断阈值大小消除噪声，但是软阈值相对平滑，容易造成信号峰值模糊的缺陷；KSVD属于稀疏表示方法，通过信号和噪声的稀疏性差异对信号降噪，避免了频域降噪的缺陷，具有较好的降噪效果，但是由于KSVD算法中忽略均值信号中的噪声，因此利用KSVD降噪具有一定的局限，而本文算法改进KSVD，进一步消除了隐藏在均值信号中的噪声，相对于其它算法，所提算法的特征状态监测正确率最高，由此说明本文算法能够更彻底的降噪和更好的保留故障特征信息。

(a) 滑动轴承中期摩擦时AE信号

(b) 原始AE信号频谱

(c) AE信号的本文算法降噪

(d) 降噪后的AE信号频谱

降噪算法滑动轴承摩擦状态监测结果/%正常润滑边界摩擦严重摩擦原信号66．676073．33EMD76．6776．6780小波软阈值86．6776．6783．33KSVD83．338086．67本文算法93．3383．3390

5 结 论

(1)通过K-SVD算法降噪的滑动轴承信号中残留噪声，经分析和验证，根源是K-SVD算法中均值标准化的缺陷；

(2)提出基于均值信号改进的K-SVD算法，该算法相比于K-SVD字典算法，在保留裂纹信号特征的前提下能更好地去除噪声，解决了均值信号降噪与信号矩阵稀疏要求的矛盾；

(3)内燃机滑动轴承磨损实例应用，表明本文算法能够更好的保留故障的信息，成功获得了滑动轴承不同程度摩擦状态的变化，证明了该算法的有效性。

[1] 王晓伟，刘占生，张广辉，等. 基于声发射的可倾瓦径向滑动轴承碰摩故障诊断[J]. 中国电机工程学报, 2009, 29(8): 64-69.

WANG Xiaowei, LIU Zhansheng, ZHANG Guanghui, et al. Rubbing fault diagnose of tilting pad journal bearing by acoustic emission[J]. Proceedings of the CSEE, 2009, 29(8): 64-69.

[2] 褚福磊, 王庆禹, 卢文秀. 用声发射技术与小波包分解确定转子系统的碰摩位置[J]. 机械工程学报, 2002, 38(3): 139-143．

CHU Fulei, WANG Qingyu, LU Wenxiu. Detection of the rub location in a rotor system with AE sensors and wavelet analysis[J]. Chinese Journal of Mechanical Engineering, 2002, 38(3): 139-143.

[3] 秦萍. 动载荷滑动轴承故障诊断的研究[D]. 成都: 西南交通大学, 2003.

[4] 易太连, 欧阳光耀, 朱石坚，等. 运用小波函数对曲轴冲击响应中不同特征信号的提取[J]. 内燃机工程, 2011, 32(5): 76-78.

YI Tailian, OUYANG Guangyao, ZHU Shijian, et al. Study on extraction of Feature signal from crankshaft shock response signal using wavelet analysis[J]. Chinese Internal Combustion Engine Engineering, 2011, 32(5): 76-78.

[5] 吴定海, 张培林, 任国全，等. 基于双树复小波包的发动机振动信号特征提取研究[J]. 振动与冲击, 2010, 29(4): 161-163.

WU Dinghai, ZHANG Peilin, REN Guoquan, et al. Feature extraction of an engine vibration signal based on dual-tree wavelet package transformation[J]. Journal of Vibration and Shock, 2010, 29(4): 161-163.

[6] ELAD M, ABARON M. Image denoising via sparse and redundant representations over learned dictionaries[J]. IEEE Transactions on Image Processing, 2006, 15(12): 3736-3745.

[7] MILANFARP C. Clustering-based denoising with locally learned dictionaries[J]. IEEE Trans on Image Pro-cessing, 2009, 18(7): 1444-1451.

[8] ENGAN K, SKRETTING K, HUSOY H J. Family of iterative LS-based dictionary learning algorithms, ILS-DLA, for sparse signal representation[J]. DigitalSignal Processing, 2007, 17(1):38-49.

[9] ELAD M, ABARON M. Image denoising via sparse and redundant representations over learned dictionaries[J]. IEEE Transactions on Image Processing, 2006, 15(12): 3736-3745.

[10] 盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 北京: 高等教育出版社, 2007.

[11] 孙增国, 韩崇昭. 基于区域分类、自适应滑动窗和结构检测的合成孔径雷达联合降斑算法[J]. 物理学报, 2010, 59(5): 3211-3212.

SUN Zengguo, HAN Chongzhao. Combined despecksling algorithm of synthetic aperture radar images based on region classification,adaptive windowing and structure detection[J]. Acta Phys. Sin, 2010, 59(5): 3211-3212.

[12] 蔡靖, 杨晋生, 丁润涛. 模糊加权均值滤波器[J]. 中国图像图形学报, 2000, 5(1): 51-53.

CAI Jing, YANG Jinsheng, DING Runtao. Fuzzy Weighted Average Filter[J]. Journal of Image and Graphics, 2000, 5(1): 51-53.

[13] YIN Chun, ZHONG Shouming, CHEN Wufan. Design of sliding mode controller for a class of fractional-order chaotic systems[J]. Communications in Nonlinear Science and Numerical Simulation, 2012, 17(1): 356-366.

[14] 秦萍, 阎兵, 李辉. 小波分析在柴油机滑动轴承接触摩擦故障的应用[J]. 内燃机工程, 2003, 24(3): 57-59.

QIN Ping, YAN Bing, LI Hui. The application of wavelet analysis in the fault diagnosis for the plain bearings contact friction of diesel engine[J]. Neiranji Gongcheng, 2003, 24(3): 57-59.

附录

特殊变量清单如下：

向量解释向量解释y采集的源信号ciY源信号CY的第i列向量x未受污染的原信号ciX原信号CX的第i列向量q均值为零，方差为σ的高斯白噪声ciQ噪声CQ中的第i列向量aK⁃SVD字典矩阵的稀疏向量s1(t)瞬时弹性波型的摩擦信号x～x～=Da～为稀疏后的AE信号s2(t)AE裂纹信号M均值信号e(t)本底信号ciYY信号中第i个列向量zs0．1dB高斯噪声biY第i列向量信号的均值标准化ciM扩展矩阵划分的第i列向量y′恢复信号M′1稀疏后的均值信号

矩阵解释矩阵解释DD∈Rn×m字典矩阵CM新均值信号矩阵CY信号矩阵LY=(CY，CM)信号扩展矩阵CY′更新的字典稀疏信号矩阵LY′稀疏后的扩展信号矩阵CY′=(b1Y′，b2Y′，…，bN-w+1Y′，)；biY′=(bi1Y′，bi2Y′，…，bijY′)T

ImprovedmethodforbearingAEsignaldenoisingbasedonK-SVDalgorithms

ZHANGJunning1,ZHANGPeilin1,HUAChunrong2,QINPing2

(1. Department 7st Ordnance Engineering College, Shijiazhuang Hebei 050003, China; 2. School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China)

For extracting the relatively weak crack information contained in plain bearing Acoustic Emission (AE) signals, in cosideration of the signal sensibility of K-SVD algorithms, an improved average signal method based on the K-SVD dictionary was proposed. The sparse and pulse signal extraction characteristics of the AE signal matrix were obtained by using the signal reorganization and expansion strategy, which avoids the mixed noise pollution on the AE signal. Then, a fuzzy weighted average filter was applied to process the remained signal, which eliminates the mixed noise pollution on the low amplitude signals. The superimposition of the average signal in K-SVD was achieved by the above two steps. Compared with the traditional K-SVD algorithm, the improved algorithm can achieve better denoising performance and more obvious fault features. The experimental results show the change of the bearings friction state, which validates the effectiveness of the algorithms at the same time.

plain bearing; acoustic emission; K-SVD; average signal

TK421

A

10.13465/j.cnki.jvs.2017.21.023

国家自然科学基金(51205405；51305454)

2016-06-13 修改稿收到日期：2016-08-08

张峻宁 男，硕士生，1992年生

张培林 男，教授，博士生导师。E-mail:rommandy@126.com