栈式稀疏加噪自编码深度神经网络的滚动轴承损伤程度诊断

陈仁祥， 杨 星， 杨黎霞， 王家序， 徐向阳， 陈思杨

(1.重庆交通大学 机电与车辆工程学院，重庆 400074；2.四川大学 空天科学与工程学院，成都 610065； 3.重庆交通大学 经济与管理学院，重庆 400074)

栈式稀疏加噪自编码深度神经网络的滚动轴承损伤程度诊断

陈仁祥1,2， 杨 星1， 杨黎霞3， 王家序2， 徐向阳1， 陈思杨1

(1.重庆交通大学 机电与车辆工程学院，重庆 400074；2.四川大学 空天科学与工程学院，成都 610065； 3.重庆交通大学 经济与管理学院，重庆 400074)

针对滚动轴承损伤程度的特征自学习提取与智能诊断问题，提出栈式稀疏加噪自编码深度神经网络的滚动轴承损伤程度诊断方法。滚动轴承损伤特征受到工况、环境噪声等干扰，浅层自编码网络对损伤特征的自学习、提取能力不足。为此，论文将稀疏项限制和加噪编码融入自编码网络，同时将自编码网络堆栈并添加分类层，构建出栈式稀疏加噪自编码深度神经网络，进行轴承损伤特征非监督自动提取与损伤程度智能诊断。稀疏项限制和深度神经网络的构建提高了特征学习能力，加噪编码的融入改善了网络的鲁棒性。所构建深度神经网络通过多层无监督逐层自学习和有监督微调，完成损伤特征自动提取与表达，并实现了损伤程度智能诊断。不同工况下轴承损伤程度诊断的实验验证证明了所提方法的可行性和有效性。

滚动轴承；损伤程度；稀疏加噪自编码；深度神经网络；诊断

滚动轴承是旋转机械的重要部件，其性能退化或失效影响整机性能及其运行可靠性。目前滚动轴承故障诊断多集中于故障分类研究，而工程中仅判断是否发生故障以及故障类型难以进行预防维护，只有对损伤程度进行准确评估和诊断才能有效指导轴承维护工作。所以，轴承损伤程度的诊断研究愈发重要。

当前国内外对于故障程度的评估与诊断主要利用信号处理技术(如傅里叶变换、包络解调、阶次分析、小波变换和EMD分解等)提取故障特征，再输入到合适分类器进行识别。窦东阳等[1]利用EMD 和Lempel-Ziv指数进行滚动轴承单点损伤程度诊断。从飞云等[2]利用Kolmogorov-Smirnov 检测方法实现了滚动轴承疲劳实验的全寿命检测。张龙等[3-4]分别在多尺度熵的基础上利用熵均值和支持向量机进行滚动轴承故障程度评估。关贞珍等[5]利用振动图像文纹理特征识别技术进行轴承故障程度诊断。以上方法取得了较好的效果，但这种传统智能诊断方法需要依靠信号处理与诊断经验提取故障特征，再利用机器学习模型进行智能诊断。在多工况交替、故障信息耦合及故障模式不明时效果欠佳。

为了直接从原始信号中学习故障特征进行故障诊断，国内外学者相继提出了故障特征的自学习方法。Liu等[6-7]采用稀疏编码进行故障特征的自学习与故障诊断，解决了特征自学习问题，但稀疏编码在样本不充足时学习效果欠佳，需要设计合适的分类器才能实现智能诊断。孙文珺等[8]采用稀疏自编码提取感应电动机故障特征。雷亚国等[9]利用深度神经网络来进行机械装备健康监测。这些研究工作为故障特征的自动学习提供了有益借鉴。

自编码(Auto-Encoder, AE)[10-11]利用非监督方式学习复杂数据的内在特征并将其简明表达，降低了分类的复杂度，进行简单的分类即可实现智能化诊断。自编码仅包括输入层、隐含层和输出层，属于浅层网络，学习能力有限，特别是在面对样本复杂度高的情况下，特征学习效果欠佳。基于此，论文将稀疏项限制和加噪编码融入自编码网络，同时将自编码网络堆栈并添加分类层，构建出一种栈式稀疏加噪自编码深度神经网络，进行滚动轴承损伤特征无监督自动提取与损伤程度智能诊断。稀疏项限制和加噪编码的融入，提高了特征提取能力与网络的鲁棒性。自编码网络的堆栈能使网络获得输入的“层次型分组”或者“部分-整体分解”结构，从而学习得到更好地表示输入数据的特征，分类层的添加使得网络具备了分类能力，实现了损伤程度智能诊断。最终，所提出栈式稀疏加噪深度神经网络通过多层无监督逐层学习和有监督微调，完成了损伤特征的自动提取与表达，并实现了损伤程度诊断。通过对不同工况下滚动轴承损伤程度诊断的实验验证结果证明了所提方法的可行性和有效性。

1 稀疏加噪自编码的原理与结构

1.1自编码的基本原理

编码过程可表示为：

h=fθ(x)=Sf(Wx+b)

(1)

式中：编码网络参数集θ={W,b}；W为d′×d维的权值矩阵；b为偏置向量；Sf为激活函数；有sigmoid和tanh两种。

解码过程可表示为：

(2)

式中：编码网络参数集θ′={W′,b′}；W′为d×d′维的权值矩阵，且有W′=WT；所以AE具有关联权值。b′为偏置向量，Sg为解码器的激活函数，一般为线性函数或sigmoid函数。

图1 AE的结构图

训练AE的过程就是就是在训练样本集D上寻找参数θ和θ′的最小化重构误差，重构误差表达式为：

(3)

式中，L为重构误差函数，一般可用平方误差函数(用于线性激活函数)或交叉熵损失函数(用于sigmoid函数)，分别表示为：

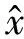
(4)

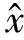
(5)

1.2稀疏性限制

在自编码中，一般情况下隐藏层的神经元数量较大甚至超过输入数据维数，所获得编码矢量h维数较高，难以体现训练样本的特定结构，不利于学习得到损伤特征的有效表达。为此，稀疏自编码在自编码器的基础上引入稀疏惩罚项将隐藏层节点的激活值约束在非激活状态值附近，控制变量规模，在隐藏层节点数量很大时仍然能够提取输入数据的结构性特征，提取高维数据变量的稀疏解释性因子，有效保留原始输入的非0特征，从而学习得到相对稀疏简明的数据特征。稀疏自编码提高了表示学习算法的提取能力，增强了数据的线性可分性，使分类边界更加清晰，使得信息表述的全面性和准确性得到显著提高[12]。

具体来讲，对AE加入稀疏性限制即对输出接近于最小值(如0)的隐藏层的神经元进行抑制，从而降低h的维数，以有利于学习得到训练样本中损伤特征的良好表达。

稀疏自编码的代价函数在原代价函数的基础上加上稀疏惩罚项，可定义为：

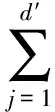
(6)

式中：β为控制稀疏性惩罚因子的权重；ρ为稀疏性参数，一般是接近于0的较小值(如ρ=0.05)；ρj为第j个神经元的平均激活值；J(W,b)为AE的代价函数，定义如下：

(7)

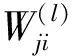
稀疏惩罚项的实质是Kullback-Leibler相对熵，描述平均值分别为ρ和ρj的两个伯努利随机变量之间分布的差异性，其表达式为：

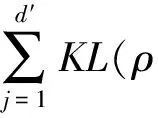
(8)

ρj可按照下式计算：

(9)

式中，aj(x(i))表示给第i个训练样本x(i)下第j个神经元的激活度。

由于希望大多数的隐藏层神经元“不活跃”以学习到特定结构，所以希望ρj趋近于ρ。当ρ=ρj时，KL(ρ‖ρj)=0，否则KL(ρ‖ρj)会随着ρj偏离ρ而逐渐增大。

整个编码的目的是得到优化的权值矩阵W和偏差b。在此，可通过采用反向传播算法(Backpropagation Algorithm，BP)来最小化代价函数Jsparse(W,b)得到优化的W和b。同时，采用梯度下降法在每一次迭代过程中更新一次权值，公式如下：

(10)

式中，α为学习速率。

通过对稀疏代价函数Jsparse(W,b)的优化得到隐藏层的稀疏表达，从而更有效学习损伤特征表达。

1.3加噪编码

为了提高自动编码器所学习得到特征的鲁棒性，Vincent等[13]通过对样本数据加入一定概率密度(通常为二项分布)的噪声后进行编码，解码时再根据噪声统计特性从未受到干扰的数据中估计出受干扰样本的原始形式，从而提高所学习得到特征的鲁棒性，降低对微小扰动的敏感性，这就是加噪编码。由于受到环境、工况、测试系统的影响，所获取的样本的特征会有所波动，要求对所学习到的损伤特征表达具有较好的鲁棒性，所以在进行稀疏自动编码过程中融入去噪编码得到稀疏加噪自动编码。

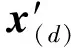
(11)

然后通过优化下式的目标函数完成加噪自编码的训练

(12)

综上所述，在AE的基础上通过加入稀疏性限制条件来所学习到更有效的损伤特征表达，同时在训练样本中加入噪声编码重构减少随机因素(如环境噪声和工况变化)对提取故障特征的影响，得到稀疏加噪自编码网络(Sparse Denoising Auto-Encoder, SDAE)，使其特征提取能力和鲁棒性更好。

2 栈式稀疏加噪自编码深度神经网络

2.1栈式稀疏加噪自编码深度神经网络的结构

SDAE仅有三层，属于浅层网络，而由于训练样本所蕴含的损伤特征的复杂性，难以通过一层隐藏层即能学习到表达能力强的故障特征。所以对SDAE进行堆栈构建出包含多层SDAE的栈式稀疏加噪自编码(Stacked Sparse Denoising Auto-Encoder，SSDAE)深度神经网络。

(13)

式中：a(l)指第l层的输出；z(l)和z(l+1)分别为第l层和第l+1层的输入。

同理，栈式神经网络的解码过程按照从后向前的顺序执行每一层自编码器的解码步骤：

(14)

式中，a(nl)是最深层隐藏单元的输出，是对输入的最高阶表达。每一层网络的训练是无监督的，即用自编码的方法使得输出值等于输入值。

在SSDAE中，因最后一个隐藏层只能输出原始数据的重构，不具有分类识别功能。所以，为了让SSDAE网络具有分类识别的功能，在最后一层隐藏层后加入分类层，分类层的神经元个数即为损伤类别数，SSDAE的结构图如图2所示。

图2 SSDAE的结构图

2.2预训练

对于SSDAE深度神经网络，采用逐层贪婪训练法对其进行预训练，基本步骤可总结如下：

步骤1 以无监督方式训练第一层SDAE，将其输出作为原始输入的最小化重构误差；

步骤2 以上一层SDAE隐藏层作为下一层SDAE的输入，训练下一层SDAE；

步骤3 重复步骤2)，完成所有SDAE的训练；

步骤4 将最后一层隐藏层的输出作为分类层的输入，分类层神经元个数为损伤类别数，为下一步有监督微调做准备。

通过预训练，建立起栈式稀疏加噪深度神经网络，获得所有隐藏层，每一层所学习到的特征就是数据特征的不同阶表达。

2.3有监督微调

在利用逐层贪婪训练法对栈式稀疏加噪自编码网络进行预训练后，需要通过带标签的样本对网络进行有监督微调，从而提升栈式自编码神经网络的性能表现。微调的核心思想是将栈式自编码神经网络的所有层视为一个模型，用有监督学习算法进一步调整经过预训练的神经网络，经过多次迭代，所有权重和偏置均得到优化。将最后一层隐藏层的输出和类标签作为分类层的输入，应用BP算法来对整个深度神经网络进行微调。其过程如下：

(1)在预训练的基础上输入有标签样本(x(i),y(i))，进行一次前馈传递，对L2层、L3层直到输出Lnl层，应用前向传播算法得到各层上的激活值；

(2)对输出层nl层，残差

δ(nl)=-(▽a(nl)J)·f′(z(nl))

(15)

式中：▽a(nl)J=θT(I-P)；I为输入数据对应的列别标签；P为条件概率向量。

(3)对l=nl-1,nl-2,…,2层，该层残差

δ(l)=((W(l))Tδ(l+1))·f′(z(nl))

(16)

(4)计算得到偏导数：

▽W(l)J(W,b;x,y)=δ(l+1)(a(l))T

▽b(l)J(W,b;x,y)=δ(l+1)

(17)

从而得到总体代价函数：

(18)

这样，就可根据式(10)微调整个网络参数。

完成预训练和有监督微调的SSDAE深度神经网络实现了损伤特征无监督自学习和有监督微调的有机结合，不同隐藏层学习到不同的特征，低阶隐藏层为高阶隐藏层提供特征模式，便于高阶隐藏层进行模式组合。SSDAE深度神经网络拓扑结构完整，具有强大的非线性拟合能力，能发现数据的分布式特征表示，提取数据的潜在分层特征，适用于在变工况和环境噪声干扰下对滚动轴承损伤程度特征的自学习提取与诊断。

3 栈式稀疏加噪自编码深度神经网络的滚动轴承损伤程度诊断算法实现

针对滚动轴承损伤程度诊断的需求与特点，提出栈式稀疏加噪自编码深度神经网络进行滚动轴承损伤程度诊断。该方法将无监督自学习与有监督微调相结合，可同时完成滚动轴承损伤程度特征自提取与损伤类型的识别，克服了传统智能诊断方法的不足。根据上文论述，为了实现所提栈式稀疏加噪自编码深度神经网络的滚动轴承损伤程度诊断，其算法实现流程图如图3所示。

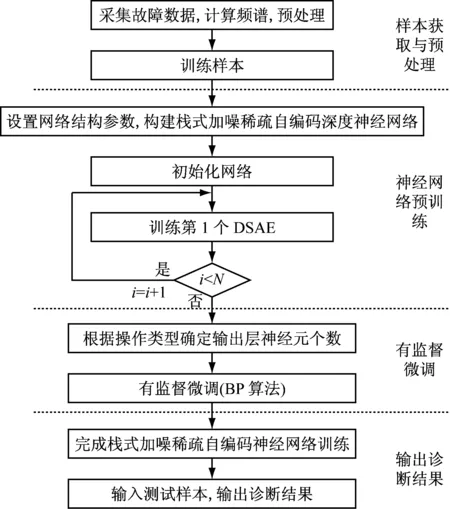
图3 诊断流程

该算法实现主要包括：

(1)样本获取与预处理。采集故障数据，计算频谱，并对频谱进行预处理(去除野点、白化)，并进行归一化使其幅值范围为[0,1]，分别获得训练样本和测试样本。经过预处理后的样本输入范围为[0,1]，在此选择sigmoid函数作为激活函数；

(2)神经网络预训练。设置网络结构参数(包括DSAE数目N，各层神经元个数，加噪比例，稀疏目标值)构建出栈式加噪稀疏自编码神经网络。输入训练样本，逐层训练N个DSAE，即将每个DSAE的输出作为下一个DSAE的输入，直到完成N个DSAE的预训练；

(3)有监督微调。根据损伤类型确定输出层神经元个数，输入有标签训练样本对预训练得到的参数进行微调，完成网络参数的训练；

(4)输出诊断结果。输入测试样本，输出诊断结果。

4 实验验证

为了验证提出方法的可行性和有效性，将提出方法应用于轴承损伤程度诊断。轴承数据来源于美国西储大学，该数据被认为是检验机械故障诊断方法的基准。轴承型号为SKF6205-RS，通过电火花加工凹槽方式在其内、外滚道和滚动体上模拟损伤，凹槽深度均为0.279 mm，凹槽宽度代表了轴承的不同损伤程度，具体损伤类型与损伤程度如表1所示。该表中，以内圈损伤为例，代号IF1/IF2/IF3分别指凹槽宽度为0.178/0.356/0.533(mm)时的损伤程度。

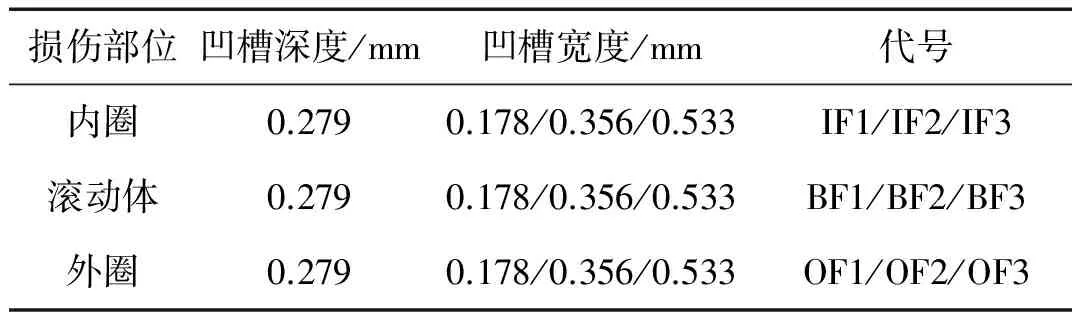
表1 损伤类型

分别在负载2HP、转速1 750 r/min和负载0HP、转速1 797 r/min两种工况下采集振动数据，采样频率为48 kHz，采样长度为485 643点，以2 048点为一段，每类损伤在两种工况下分为可获得237个样本。对于每类损伤，在两种工况下分别随机抽取100个样本，共计200个样本作为训练样本。在剩下的样本中，每种工况下随机抽取100个样本，共计200个样本作为测试样本。首先计算样本的频谱，原始信号及其频谱结果如图4所示(仅给出IF1、BF1、OF1三种故障类型)。观察该图，同种损伤类型在不同工况下采集的振动信号的时域波形、频谱能量、主频及频谱结构均存在差异。

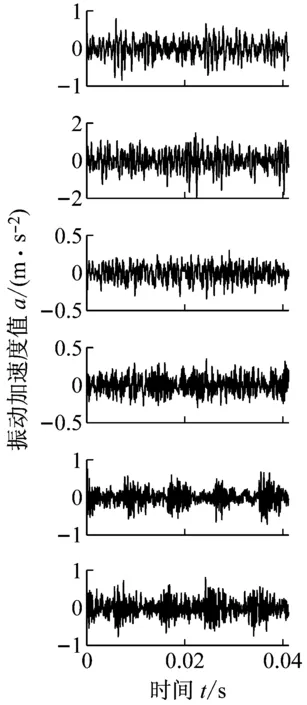
首先，对比分析提出方法的特征自学习提取能力。分别应用人工提取特征、稀疏自编码、论文提出方法提取损伤特征。

人工提取特征方法中，提取反映轴承振动信号时、频域特征的有效值、方差、峭度指标和重心频率等24个特征值(具体见文献[14])构建出刻画轴承振动信号的特征集，再对其进行非线性约简，然后应用SVM进行分类识别。为了便于观察，特征集约简目标维数为3，提取结果如图5(a)所示。人工提取特征方法得到结果中不同损伤部位及损伤程度的特征相互重叠交叉在一起，没有被很好的分开。同时，相同损伤类型的特征聚集性也不好，如BF1、OF2均被分成两部分。原因分析如下：通过人工方式提取的特征依赖人的经验，难以获得对轴承损伤程度的表征效果好的特征。同时，所提取的特征量(如有效值、方差等有量纲的特征量)受到工况的影响，导致同种损伤时不同工况下提取的特征也相互区分，不能实现不同工况下损伤特征的同尺度表征。

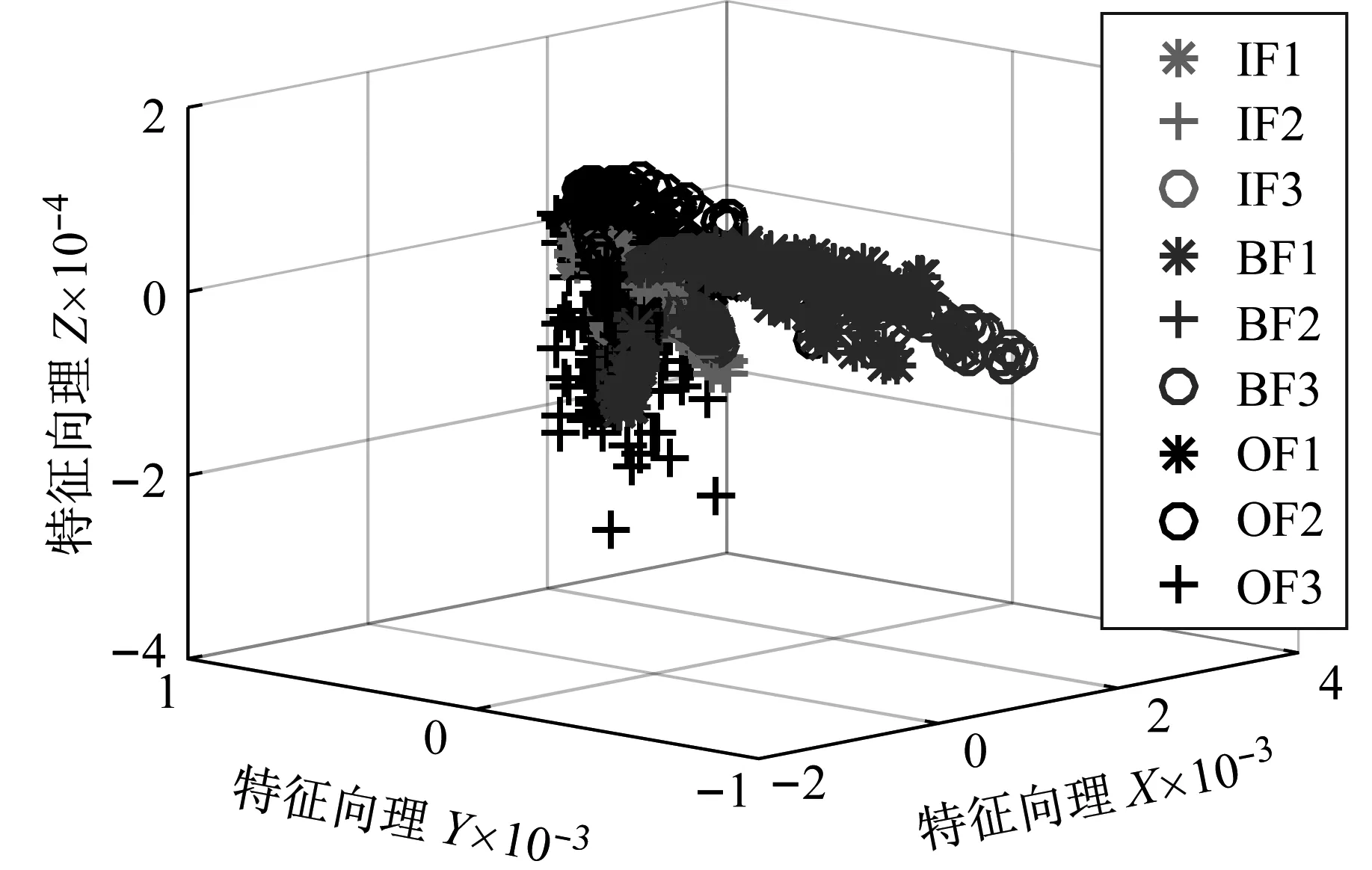
(a)人工提取特征

(b)稀疏自编码

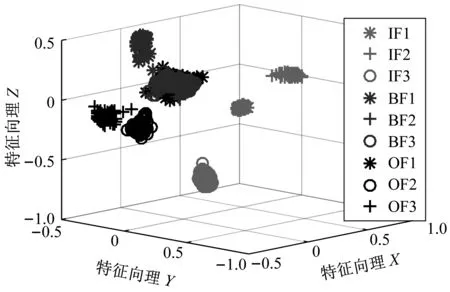
(c)提出方法

应用稀疏自编码和提出方法对样本频谱数据进行自学习得到损伤特征后，应用主成分分析方法得到前三个主分量作为特征向量，结果如图5(b)和(c)所示。稀疏自编码的输入为频谱数据(取800线)，即输入层神经元个数为800，网络结构为800-300-800，稀疏惩罚因子的权重β=0.5，为稀疏性参数ρ=0.05。稀疏自编码得到的结果，虽同种损伤类别的聚集性优于人工提取特征方法，但不同损伤类别间也存在一定程度的重叠交叉。这是由于稀疏自编码只有一层隐藏层，对数据本身特征学习不足，提取特征效果不佳。

在应用提出方法进行特征自学习时，一般来讲，在SSDAE深度学习网络的结构中，包含SDAE层数越多即深度越深则网络的特征学习效果越好，但过深的网络结构会增大网络训练难度。经过前期试验，这里采用包含三层SDAE的SSDAE，每层SDAE神经元个数分别是：800-300-800,300-100-300,100-50-100，分类层神经元个数与损伤类别相同为9。经过前期反复试验确定相关参数如下：稀疏性惩罚因子的权重β=0.5，为稀疏性参数ρ=0.05，加入噪声比例为20%。应用提出方法得到的结果不仅同种损伤类别特征的聚集性好，而且不同损伤类别之间被很好的分开，说明这种方法所学习提取得到的损伤特征更为有效。同时，由图5(c)可知，同种损伤形式在不同工况下的特征聚集在一起，说明所提取特征受工况干扰小。同种损伤形式的不同损伤程度相对集中，不同损伤形式的特征分布于不同的区域。

进一步，对比分析诊断率。表2为应用人工提取特征、稀疏自编码和提出方法得到的诊断精度，其中“两种工况”指训练样本和测试样本中均包括两种工况下的样本，“一种工况”指训练样本和测试样本均来自于同种工况。为了避免偶然因素影响，该表中的试验结果都是由10次随机试验结果取平均所得。计算耗时的计算机配置为Intel Celore i7-3770处理器，软件为MATLAB2015B，1T硬盘，8G内存，

人工提取特征方法在对于训练样本和测试样本均有两种工况和只有一种工况时的平均诊断率分别为51.7%和81.4%，均较低，这是前文所述人工提取特征不易得到反映损伤程度良好的特征，同时所提取的特征的表征能力往往受到工况的影响，两种工况的诊断率低于一种工况就说明了这一点。稀疏自编码也存在两种工况下的诊断率低于一种工况的情况，这是由于这种特征学习能力本就不佳的浅层网络受工况干扰影响大，导致诊断率低。论文提出方法无论是在两种工况还是一种工况下均得到了98%以上的诊断率，是由于提出方法自适应提取损伤特征能力更强，且受到工况干扰小，鲁棒性好。在耗时方面，由于提出方法需要训练多层深度网络导致耗时较多，在实时性要求高的场合需要进一步研究快速训练算法。

通过以上实验验证，证明了所提方法能根据信号本身的特点自适应的学习、提取滚动轴承损伤特征，且鲁棒性好，受工况影响小。证明了所提方法的可行性和有效性。

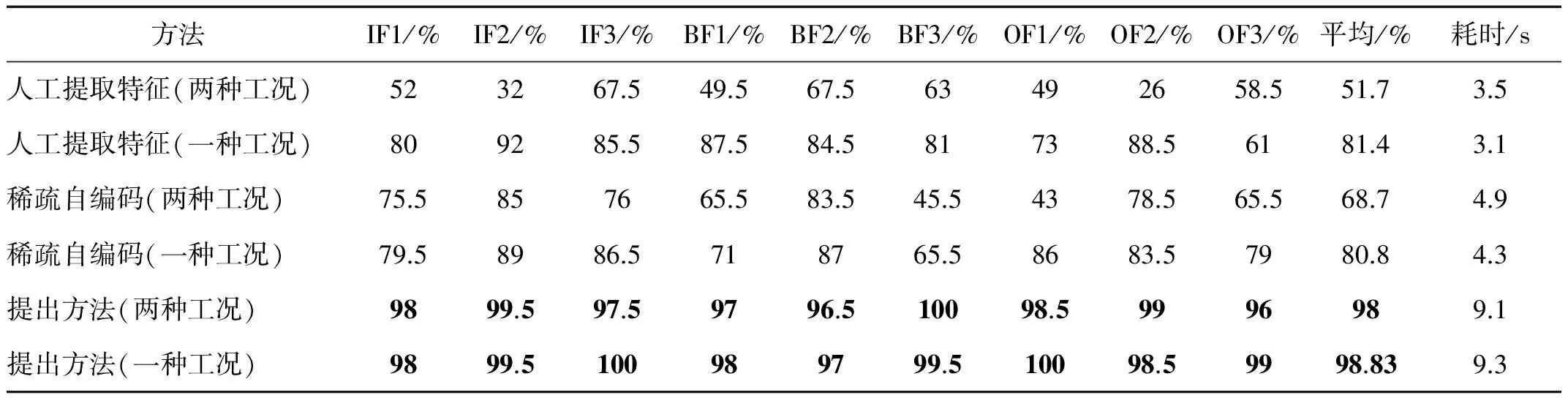
表2 诊断精度对比

6 结 论

针对滚动轴承不同损伤程度的特征自学习提取与智能诊断问题，将稀疏项限制和加噪编码融入自编码网络，同时将自编码网络堆栈并添加分类层，构建出栈式稀疏加噪自编码深度神经网络，进行轴承损伤特征非监督自动提取与损伤程度智能诊断。所构建的栈式稀疏加噪自编码深度神经网络通过对无标签数据无监督学习和有监督微调的方式完成神经网络的训练，能够自适应的学习提取轴承损伤特征，且受工况影响小，同时在分类层实现损伤程度的智能诊断。实验验证和对比分析证明了所提方法具有良好特征自适应提取能力和诊断精度，为滚动轴承损伤程度诊断提供了一种新的思路和方法。

本文后续工作主要在以下两方面：

(1)在深度神经网络训练过程中，需要通过多次试验才能确定较好的超参数(如网络层数、神经元个数、稀疏性参数等)，后续将开展超参数设置方面的研究；

(2)开展所提取特征在多层网络特征空间中的可视化研究。

[1] 窦东阳,赵英凯.基于EMD 和Lempel-Ziv 指标的滚动轴承损伤程度识别研究[J].振动与冲击,2010,29(3):5-8.

DOU Dongyang, ZHAO Yingkai. Fault severity assessment for rolling element bearings based on EMD and Lempel-Ziv index[J]. Journal of Vibration and Shock,2010, 29(3):5-8.

[2] 从飞云,陈进,董广明.基于AR模型的Kolmogorov-Smirnov 检验性能退化及预测研究[J]. 振动与冲击,2012, 31(10):79-82.

CONG Feiyun, CHEN Jin, DONG Guangming. Performance degradation assessment by Kolmogorov-Smirnov test and prognosis based on AR model[J]. Journal of Vibration and Shock,2012, 31(10):79 -82.

[3] 张龙,黄文艺,熊国良.基于多尺度熵的滚动轴承故障程度评估[J].振动与冲击,2014,33(9):185-189.

ZHANG Long, HUANG Wenyi, XIONG Guoliang. Assessment of rolling element bearing fault severity using multi-scale entropy[J].Journal of Vibration and Shock, 2014, 33(9): 85-189.

[4] WU S D, WU C W, WU P H, et al. Bearing fault diagnosis based on multiscale permutation entropy and support vector machine[J]. Entropy, 2012,14:1343-1356.

[5] 关贞珍,郑海起,叶明慧.基于振动图像纹理特征识别的轴承故障程度诊断方法研究[J].振动与冲击,2013,32(5): 127-131.

GUAN Zhenzhen, ZHENG Haiqi, YE Minghui. Bearing fault severity assessment based on vibration image[J]. Journal of Vibration and Shock, 2013,32(5): 127-131.

[6] LIU H, LIU C, HUANG Y. Adaptive feature extraction using sparse coding for machinery fault diagnosis[J]. Mechanical Systems and Signal Processing,2011,25(2):558-574.

[7] 朱会杰,王新晴,芮挺，等.基于频域信号的稀疏编码在机械故障诊断中的应用[J].振动与冲击,2015,21(34):59-64.

ZHU Huijie, WANG Xinqing, RUI Ting, et al. Application of sparse coding based on frequency domain signals in machinery fault diagnosis[J]. Journal of Vibration and Shock, 2015,21(34):59-64.

[8] 孙文珺,邵思羽,严如强.基于稀疏自动编码深度神经网络的感应电动机故障诊断[J].机械工程学报, 2016, 52(9): 65-71.

SUN Wenjun, SHAO Siyu,YAN Ruqiang. Induction motor fault diagnosis based on deep neural network of sparse auto-encoder[J].Journal of Mechanical Engineering, 2016,52(9):65-71.

[9] 雷亚国,贾峰,周昕，等.基于深度学习理论的机械装备大数据健康监测方法[J].机械工程学报,2016,21(51):49-55.

LEI Yaguo, JIA Feng,ZHOU Xin, et al. A deep learning-based method for machinery health monitoring with big data[J].Journal of mechanical engineering, 2016,21(51):49-55.

[10] TAN C C, ESWARAN C. Reconstruction and recognition of face and digit images using autoencoders[J]. Neural Computing and Applications, 2010,19(7):1069-1079.

[11] VINCENT P, LAROCHELLE H, LAJOIE I, et al. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion[J]. Journal of Machine Learning Research,2010,11(6): 3371-3408.

[12] BENGIO Y,LAMBLIN P,POPOVICI D.Greedy layerwise training of deep networks in Advances[C]//Proc of the 20thIn-ternational Conference on Neural Information Processing Systems. Cambridge: MIT Press,2007:153-159.

[13] VINCENT P, LAROCHELLE H, BENGIO Y, et al. Extracting and composing robust features with denoising autoencoders[C] // Proceedings of the 25th International Conference on Machine Learning. July 5-9，2008，Helsinki，Finland：1096-1103.

[14] LI Feng, WANG Jiaxu, TANG Baoping, et al. Life grade recognition method based on supervised uncorrelated orthogonal locality preserving projection and K-nearest neighbor classifier[J].Neurocomputing,2014(138):271-282.

Faultseveritydiagnosismethodforrollingbearingsbasedonastackedsparsedenoisingauto-encoder

CHENRenxiang1,2，YANGXing1，YANGLixia3，WANGJiaxu2，XUXiangyang1，CHENSiyang1

(1.School of Mechantronics and Vehicle Engineering, Chongqing Jiaotong University, Chongqing, 400074, China; 2. School of Aeronautics&Astronautics, Sichuan University, Chengdu, 610065, China; 3. School of Economics and Management, Chongqing Jiao tong University，Chongqing 400074, China)

Aiming at the self-taught learning of fault severity features and the intelligent diagnosis for rolling bearings, a fault severity diagnosis method based on a stacked sparse denoising auto-encoder was proposed. The fault severity feature of rolling bearings is easy to be disturbed by the operating conditions and noises, and shallow networks are usually lack of enough ability in the self-taught learning and fault feature extraction. Therefore, a sparsity penalty term and a denoising encoder were the fused into the auto-encoder. Moreover, the auto-encoder network was stacked and a classification layer was added to construct the stacked sparse denoising auto-encoder deep neural network and to achieve the unsupervised feature extraction and intelligent diagnosis for rolling bearings. The ability of feature learning was improved by the sparsity penalty term and stacked auto-encoder, and the robustness of network was improved by the denoising encoder. The fault feature was automatically extracted and expressed to realize intelligent diagnosis, through training the layers individually without supervision and fine tuning with supervision. The feasibility and validity of the present method were verified by its application in diagnosing the fault severity of rolling bearings under different operation conditions.

rolling bearing; fault severity; stacked sparse denoising auto-encoder; deep neural network; diagnosis

TN911.7; TH165.3

A

10.13465/j.cnki.jvs.2017.21.019

国家自然科学基金(51305471)；中国博士后科学基金(2014M560719；2016M590861)；重庆市基础与前沿研究计划资助项目(cstc2014jcyjA70009；cstc2015jcyjA70012)；重庆市教育委员会科学技术研究(KJ1400308)；国家留学基金(201408505081)

2016-07-27 修改稿收到日期：2016-08-31

陈仁祥 男，博士，副教授，1983年9月生

王家序 男，博士，教授，博士生导师，1954年6月生。E-mail:jxwang@cqu.edu.cn