半空间双相压电介质垂直边界附近圆形夹杂的动态性能分析

张希萌， 齐 辉， 丁晓浩， 陈洪英

(哈尔滨工程大学 航天与建筑工程学院,哈尔滨 150001)

半空间双相压电介质垂直边界附近圆形夹杂的动态性能分析

张希萌， 齐 辉， 丁晓浩， 陈洪英

(哈尔滨工程大学 航天与建筑工程学院,哈尔滨 150001)

利用“Green函数法”和“镜像法”对在SH波作用下半空间双相压电介质垂直边界附近圆形夹杂的动态性能进行分析，得到其稳态响应。利用镜像法得到满足水平边界应力自由与电位移自由的波函数解析表达式。根据垂直边界连续性条件，利用“契合法”建立第一类Fredholm型积分方程组，得到圆形夹杂周边的动应力集中系数与电场强度系数解析表达式。数值算例分析了入射波频率、入射角度、圆形夹杂位置等对动应力集中系数与电场强度系数的影响，并与已有文献进行比较。

半空间；双相压电介质；圆形夹杂；SH波；动应力集中系数；电场强度集中系数

压电介质具有机-电耦合效应，可实现机械振动和交流电的互相转换，这使压电介质广泛应用于智能结构和传感器元件中，实现结构的自我诊断、自我修复等功能，因此在未来航空航天飞行器设计中占重要地位。由于加工工艺、环境变化等因素，复合材料会产生圆孔或夹杂等缺陷，这些缺陷若存在于界面附近处，即材料性质变化最剧烈的地方，将会出现材料失效、破坏等问题。比如压电元件在生产加工过程中形成的圆形夹杂，其动应力集中问题比一般材料更复杂。大量学者对缺陷问题进行研究并取得丰富成果。近年来，舒小平等[1]利用等效单层理论求解了正交压电复合材料层板在各类边界条件下的解析解，周志东等[2]利用stroh理论分析了含界面刚性线夹杂的双压电介质的电弹性问题，侯密山等[3]利用复变函数中级数展开法研究了含任意形状夹杂压电介质的反平面问题，Shindo等[4]利用波函数展开法分析了在剪切波与电载荷作用下含柱形夹杂的无限大压电介质的动态性能，Du等[5]利用波函数展开法对部分脱胶夹杂对反平面剪切波的散射问题进行了研究，Feng等[6]利用奇异积分方程技术研究了压电材料中脱胶夹杂对SH波的散射问题，宋天舒等[7-9]研究了全空间双相压电介质中水平边界附近圆孔的动力学问题。

本文利用“Green函数法”和“镜像法”，构造出满足水平边界应力自由与电位移自由、垂直边界连续性条件的波函数。根据直角域公共垂直边界上连续性条件，利用“契合法”建立第一类Fredholm型积分方程组并进行求解。文章最后给出具体算例和数值结果，讨论了入射角度、入射频率、圆形夹杂位置等对动应力集中系数与电场强度集中系数的影响。

1 问题的描述

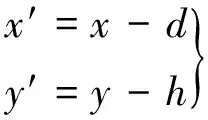
(1)

图1 含圆形夹杂的半空间双相压电介质模型

Fig.1 The model of a piezoelectric bi-material half-space with a circular inclusion

本文模型是对实际工程中由两种压电介质组成的含圆形夹杂缺陷的压电元件在SH波作用下动态性能问题的简化。

2 Green函数

设z轴为压电材料的电极化方向，则反平面动力学问题的稳态控制方程(忽略时间因子e-iωt)表达式为：

(2)

式中：w,φ和ω分别为压电材料出平面位移、电位势和SH波圆频率。方程(1)可以简化为：

(3)

(4)

(5)

式中：τrz与τθz表示剪应力，Dr与Dθ表示电位移。本节研究的直角域介质Ⅰ在线源荷载δ(η-η0)作用下的模型如图2所示。η0=d+yi(y≤h)，表示介质Ⅰ中的点。

图2 受线源荷载作用的直角域模型

Fig.2 The right-angle plane model impacted by a line source force

本节研究的直角域介质Ⅰ的边界条件可以表示为：

(6)

(7)

(8)

式中：

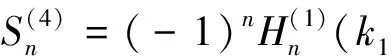
其中：η1=η-2hi,η2=η1-2d,η3=η-2d

(9)

对于介质Ⅲ圆形夹杂内部的驻波，其表达式为：

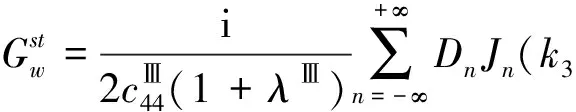
(10)

(11)

利用边界条件(6)建立关于An、Bn、Cn、Dn、En、Fn的方程组：

(12)

式中：

ξ(4)=0

其中：

ι=Jn-1(k3η)[η/η]n-1,

ν=-Jn-1(k3η)[η/η]n+1,

将方程(12)等式两端同时乘以exp(-imθ)，m=0,±1,±2,±3…，在边界ΓC上从(-π,π)进行积分，截取有限项，得到关于An、Bn、Cn、Dn、En、Fn的线性方程组进行求解。对于介质Ⅱ，其Green函数表达式为：

(13)

3 SH波的散射

根据文献[9-11]中方法，入射波wi、反射波wr、折射波wf和散射波ws以及激发的电位势函数φi、φr、φf和φs表达式分别如下：

(14)

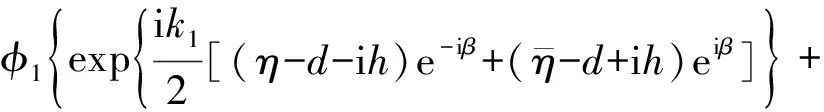
(15)

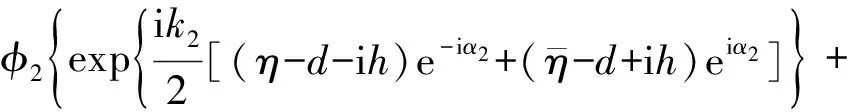
(16)

(17)

(18)

式中：β0=π-α0,α0为入射角度，α2为折射角度。各个常系数满足连续性条件：

(19)

在SH波作用下产生的散射波场中未知量Kn、Pn、Qn、Rn、Sn、Tn可以根据边界条件(6)进行求解，方法与求解Green函数中未知量所用方法相同。

4 契 合

图3 含圆形夹杂的半空间双相压电介质垂直界面的契合

Fig.3 Conjunction of Piezoelectric Bi-material vertical interface in half space with a circular inclusion

在介质Ⅰ中：

(20)

在介质Ⅱ中：

(21)

WⅠ+Wf1=WⅡ+Wf2,

φⅠ+φf1=φⅡ+φf2

(22)

由位移与电势的连续性条件式(19)对式(22)进行简化，得到关于外力系的积分方程：

(23)

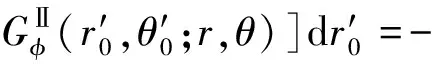
(24)

5 动应力集中系数

根据文献[10]，在SH波作用下夹杂周边的环向剪切应力可以表示为：

(25)

动应力系数可表示为：

6 电场强度集中系数

根据文献[10]，在SH波作用下夹杂周边的环向剪切应力可以表示为：

(26)

7 具体算例

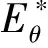
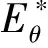
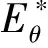
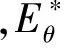
图5 SH 波以不同角度入射时圆形夹杂周边动应力集中系数的分布

Fig． 5 Distribution of DSCF around circular inclusion edge by SH-wave with different incident angles.

图6 SH波水平入射时圆形夹杂周边动应力集中系数随ka的分布

Fig.6 Distribution of DSCF around circular inclusion edge vs.kaby SH-wave horizontally

图7 SH波水平入射时圆形夹杂周边动应力集中系数随λⅠ的分布

Fig.7 Distribution of DSCF around circular inclusion edge vs.λⅠby SH-wave horizontally

图8 SH波水平入射时圆形夹杂周边动应力集中系数随λⅡ的分布

Fig.8 Distribution of DSCF around circular inclusion edge vs.λⅡby SH-wave horizontally

图9 SH波水平入射时圆形夹杂周边动应力集中系数随h*的分布

Fig.9 Distribution of DSCF around circular inclusion edge vs.h*by SH-wave horizontally

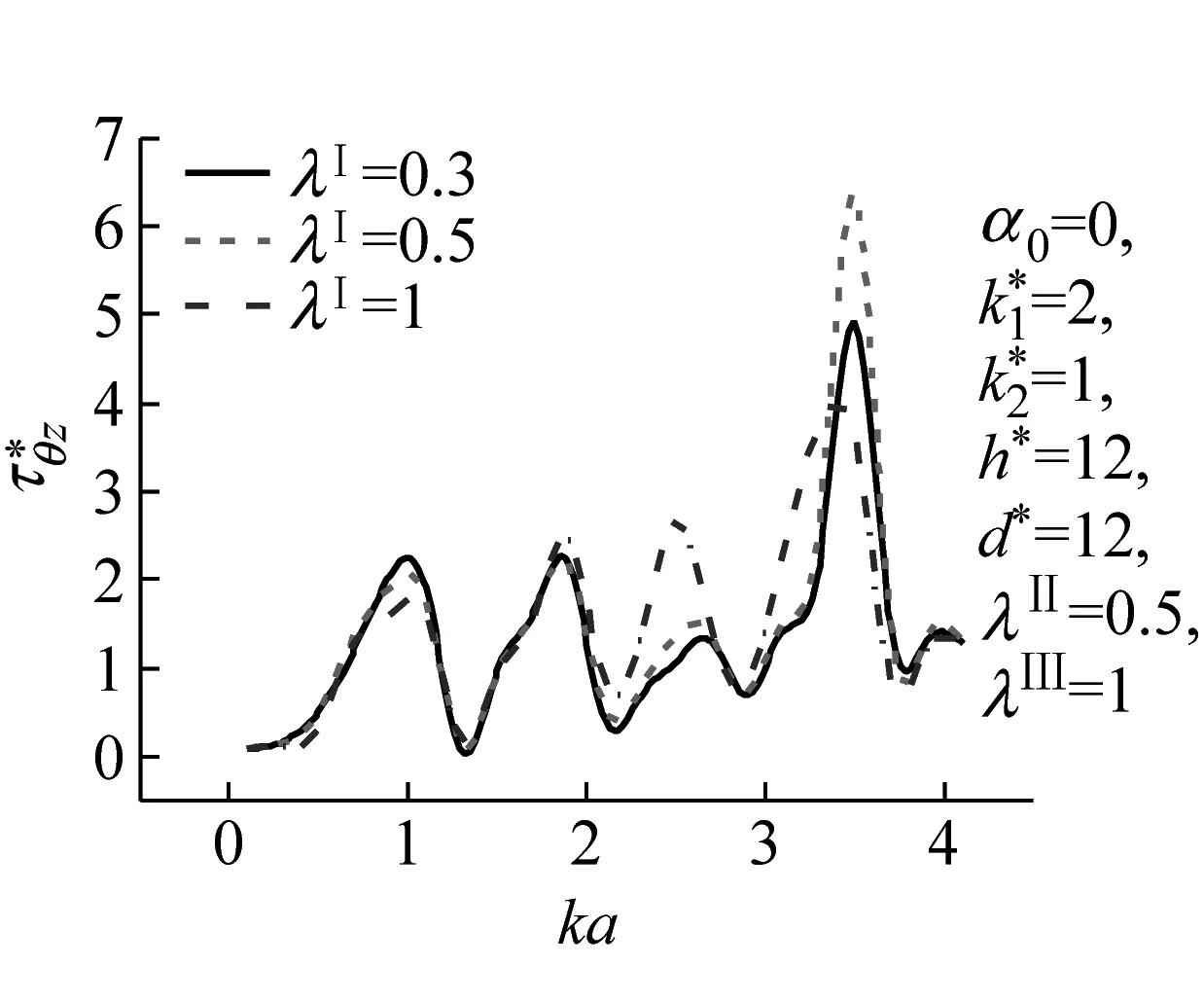
图10 SH波水平入射时圆形夹杂周边动应力集中系数随ka的变化

Fig.10 Variation of DSCF around circular inclusion edge vs.kaby SH-wave horizontally

图11 SH波以不同角度入射时圆形夹杂周边电场强度系数的分布

Fig.11 Distribution of EFICF around circular inclusion edge by SH-wave with different incident angles

图12 SH波水平入射时圆形夹杂周边电场强度系数随波数ka变化情况

Fig.12 Distribution of EFICF around circular inclusion edge vs.kaby SH-wave horizontally

图13 SH波水平入射时圆形夹杂周边电场强度系数随λⅠ的分布

Fig.13 Distribution of EFICF around circular inclusion edge vs.λⅠby SH-wave horizontally

图14 SH波水平入射时圆形夹杂周边电场强度系数随λⅡ的分布

Fig.14 Distribution of EFICF around circular inclusion edge vs.λⅡby SH-wave horizontally

图15 SH波水平入射时圆形夹杂周边动应力集中系数随h*的分布

Fig.15 Distribution of EFICF around circular inclusion edge vs.h*by SH-wave horizontally

8 结 论

图16 SH波水平入射时圆形夹杂周边电场强度系数随ka的变化

Fig.16 Variation of DSCF around circular inclusion edge vs.kaby SH-wave horizontally

本文利用Green函数法、“镜像法”、“契合法”对半空间双压电介质垂直边界附近圆形夹杂对SH波的散射进行分析研究，为压电元件的设计制造及工程应用提供了大量的参考数据。计算表明，入射角度、波数、无量纲压电参数、夹杂位置均对圆形夹杂周边的动应力强度系数与电场强度系数存在影响，高频SH波水平入射对本文模型危害较大；随着入射波频率的增加，圆形夹杂周边动应力集中系数与电场强度系数均呈现出振荡性；圆形夹杂周边动应力集中系数与电场强度系数随夹杂与水平边界距离的增加而减小；特定物理参数的两种压电介质能够减小圆形夹杂周边的动应力和电场强度，因此适当选取不同的参数组合可以降低结构破坏的可能性。

[1] 舒小平. 正交压电复合材料层板各类边界的解析解[J]. 工程力学, 2013, 30(10): 288-295.

SHU Xiaoping. Analytical solutions of cross-ply piezoelectric composite laminates with various boundary conditions [J]. Engineering Mechanics, 2013, 30(10): 288-295.

[2] 周志东，赵社戌，匡震邦.含界面刚性线夹杂与广义压电位错双压电介质的电弹性分析[J]. 固体力学学报, 2008, 29(3): 223-230.

ZHOU Zhidong, ZHAO Shexu,KUANG Zhenbang. Electroelastic analysis of bi-piezoelectrics embedded interfacial rigid lines with generalized piezoelectric dislocaton [J]. Chinese Journal of Solid Mechanics, 2008, 29(3): 223-230.

[3] 侯密山, 高存法. 压电材料反平面应变状态的任意形状夹杂问题[J].应用数学和力学, 1997, 14(1): 135-141.

HOU Mishan,GAO Cunfa.The antiplane strain problems for piezoelectric medium containing an arbitrary inclusion[J]. Chinese Journal of Applied Mathematics, 1997, 14(1): 135-141.

[4] SHINDO Y, MORIBAYASHI H, NARITA F. Scattering of antiplane shear waves by a circular piezoelectric inclusion embedded in a piezoelectric medium subjected to a steady-state electrical load[J].ZAMM Zeitschrift fur Angewandte Mathematik und Mechanik, 2002, 82(1): 43-49.

[5] DU J K, SHEN Y P,WANG X. Scattering of anti-plane shear waves by a partially debonded piezoelectric circular cylindrical inclusion[J]. Acta Mechanica, 2002, 158: 169-182.

[6] FENG W, WANG L, JIANG Z, et al. Shear wave scattering from a partially debonded piezoelectric cylindrical inclusion[J].Acta Mechanica Solida Sinica, 2004, 17(3): 258-269.

[7] 宋天舒,刘殿魁,于新华. SH波在压电材料中的散射和动应力集中[J]. 哈尔滨工程大学学报，2002，23(1): 120-123.

SONG Tianshu,LIU Diankui,YU Xinhua. Scattering of SH-Wave and dynamic stress concentration in a piezoelectric medium with a circular hole[J]. Journal of Harbin Engineering University，2002，23(1): 120-123.

[8] 宋天舒,刘殿魁,付国庆. 含刚性圆柱夹杂压电介质的动力反平面特性[J].哈尔滨工程大学学报，2003,24(5)：574-577.

SONG Tianshu,LIU Diankui,FU Guoqing.Dynamic anti-plane characteristic of piezoelectric medium with rigid cylindrical inclusion[J]. Journal of Harbin Engineering University， 2003，24(5):574-577.

[9] HASSAN1 A,SONG T S.Dynamic anti-plane analysis for two symmetrically interfacial cracks near circular cavity in piezoelectric bi-materials[J]. Applied Mathematic and Mechanics,2014，35(10):1261-1270.

[10] 李冬,宋天舒. 双相压电介质中界面附近圆孔的动态性能分析[J]. 振动与冲击，2011，30(3): 91-95.

LI Dong,SONG Tianshu. Dynamic performance analysis of circular cavity near interface in piezoelectric biomaterials [J]. Journal of Vibration and Shock， 2011，30(3): 91-95.

[11] WANG X D. On the dynamic behavior of interfacial cracks in piezoelectric media [J]. Int. J. Solids and Structures,2001, 38: 815-831.

[12] 林宏,刘殿魁. 半无限空间中圆形孔洞周围SH波的散射[J]. 地震工程与工程振动,2002, 22(2): 9-16.

LIN Hong,LIU Diankui. Scattering of SH-wave around a circular cavity in half space [J]. Journal of Earthquake Engineering and Engineering Viberation,2002, 22(2): 9-16.

[13] 折勇,齐辉,杨在林. SH波对直角平面区域内圆形孔洞的散射与地震动[J]. 应用力学学报,2008, 25(3): 392-397.

SHI Yong,QI Hui,YANG Zailin. Scattering of SH-wave by circular cavity in right-angle plane and seismic ground motion [J]. Chinese Journal of Solid Mechanics, 2008, 25(3): 392-397.

Dynamicperformanceanalysisofcircularinclusionsneartheverticalboundaryinthepiezoelectricbi-materialhalf-space

ZHANGXimeng,QIHui,DINGXiaohao,CHENHongying

(College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin, Heilongjiang 150001, China)

The dynamic performance of circular inclusion near the vertical boundary in the piezoelectric bi-material half-space under the action of SH wave was analyzed by using the Green function method and mirror method to obtain the steady state responses. An analytical expression of the wave function which satisfies the stress free and electric displacement free on the horizontal boundaries was obtained by the mirror method. According to the continuity condition on the vertical boundary, the first kind of Fredholm integral equations was established to obtain the analytical expressions of the dynamic stress concentration factor and electric field intensity concentration factor around the edges of circular inclusions by the conjunction method. The influences of the frequencies of incident wave, the incident angle and the position of circular inclusions, etc. on the dynamic stress concentration factor and electric field intensity concentration factor were analyzed and compared with the results in the calculation examples of existing literatures.

half space; piezoelectric bi-material; circular inclusion; SH wave; dynamic stress concentration factor (DSCF); electric field intensity concentration factor (EFICF)

O343

A

10.13465/j.cnki.jvs.2017.21.013

黑龙江省自然科学基金(A201404)

2016-03-25 修改稿收到日期：2016-08-16

张希萌 男，博士生，1989年生

齐辉 男，教授，博士生导师，1963年生。E-mail:qihui205@sina.com