基于包络角域加窗同步平均太阳轮故障特征提取

王志乐， 郭 瑜, 伍 星

(昆明理工大学 机电工程学院 云南省高校振动与噪声重点实验室，昆明 650500)

基于包络角域加窗同步平均太阳轮故障特征提取

王志乐， 郭 瑜, 伍 星

(昆明理工大学 机电工程学院 云南省高校振动与噪声重点实验室，昆明 650500)

行星齿轮箱广泛应用于风电机组等大型装备中，其振动特征提取在故障诊断领域有重要意义。但由于存在非平稳、调制、传递路径复杂、传递路径具有时变特性等特点，导致故障响应微弱，往往被强背景噪声所湮没。主要针对包络分析、加窗同步平均、计算阶比跟踪相结合，提出了一种适合弱特征信号解调、时变传递路径及变速工况的包络角域加窗同步平均技术。Tukey窗函数对故障振动信号进行加窗处理，希尔伯特变换(Hilbert)获取故障复包络信号，计算阶比跟踪对复包络信号进行等角度重采样，转换为准平稳角域信号，然后进行同步平均。该方法对太阳轮故障实测振动信号进行分析，实验结果表明，所提出方法能够有效地提取太阳轮故障的特征信息。

行星齿轮箱；包络分析；加窗同步平均；计算阶比跟踪

行星齿轮箱广泛应用于风电机组等大型装备中，其振动特征提取在故障诊断领域有重要意义，目前其已成为故障诊断领域的重要研究对象[1]之一。行星齿轮箱传动系统包括太阳轮、行星轮、行星架和齿圈等，行星轮的转动既包括相对自身转轴的自转，又包括绕着太阳轮的公转，并且行星轮和太阳轮、齿圈同时啮合，是典型的复合运动。在行星齿轮箱故障诊断中，传感器拾取的故障源(如太阳轮、行星轮等局部故障)对应的振动响应微弱，因经过较为复杂传输路径的衰减，其故障响应极其微弱，往往被强背景噪声所湮没。

同步平均方法[2](SA)用于从复合信号中提取指定周期分量，已成为齿轮箱振动信号去噪、提高信噪比的重要方法之一。但同步平均是对信号按选定转轴周期的整数倍进行截断，各段信号按键相信号对齐相位进行平均，而行星齿轮箱由于行星轮公转引起的振动传递路径不断变化，传感器拾取信号相位、幅值会发生变化，因此，传统同步平均方法并不适合行星齿轮箱。为解决上述问题，20世纪90 年代，国外学者，McFadden[3]提出分段加窗平均法，其可减小振动传递路径变化对信号的影响；之后Samuel等[4]提出了改进的加窗法，当行星轮或太阳轮与齿圈的齿数存在公因子时，可用多传感器对信号进行拾取和分析；Lewicki等[5]提出振动分离技术，应用于行星齿轮箱故障信号分析；Krzywda等[6]研究了基于加窗同步平均和非连续分离算法的太阳轮故障诊断。在国内，雷亚国等[7]提出了一种行星齿轮箱轮齿故障弱特征信号检测方法；冯志鹏等[8-10]研究了基于内禀时间尺度分解的联合幅值和频率解调的行星齿轮箱主要部件弱故障特征信号检测方法、局部故障振动频谱特征、频率解调分析等方法，并将这些方法应用于行星齿轮箱故障特征提取中，都取得一定的成果。但是，上述主要是针对行星轮研究，对太阳轮故障的研究甚少。阶比分析[11]是目前常用的旋转机械变速运行过程非平稳振动有效分析方法，其通过等角度采样将时域非平稳信号转变为角域准平稳信号。使其能满足傅里叶变换对信号平稳性的要求，但阶比分析对齿轮箱中齿轮等早期故障对应的微弱信号，尤其是在强干扰条件下，往往不能有效分析。包络分析(又称为共振解调分析)是用于弱信号提取的有效工具，在滚动轴承、齿轮等故障诊断中具有广泛的应用。本文所提方法主要针对传感器拾取的故障源(太阳轮局部故障)对应的振动响应，因经过较为复杂的时变传输路径的衰减，其故障响应复杂且微弱。结合加窗同步平均消除时变传递路径的优势和包络分析在弱特征信号提取方面的优势，通过获取高频共振信号其包络中含有的低频故障特征信息，对其故障信号进行高信噪比解调分析(本文主要应用希尔伯特进行包络分析)。而传统太阳轮故障特征提取主要是基于加窗同步平均的谱分析，对弱信号的提取效果不佳。因此，提出一种适合弱特征信号解调、时变传递路径及变速工况的包络角域加窗同步平均技术。

1 包络分析原理简介

包络分析(又称为共振解调分析)是一种通过获取高频共振信号其包络中含有的低频故障特征信息，对弱特征信号进行高信噪比解调的方法。包络分析分为共振信号提取和包络解调两部分，其工作原理为：轴承或齿轮等零部件发生局部损伤，其会产生周期性的(宽频)瞬时冲击，可激起传感器、齿轮箱壳体等周围结构的高频固有振动，利用带通滤波技术提取共振区附近高频谐振信号，再通过包络提取等技术解调出高信噪比包络信号。常用解调方法有：Hilbert解调、小波解调、谱峭度解调等，其中以Hilbert解调方法应用最为广泛。Hilbert变换定义为[12-13]：

*y(t)

(1)

(2)

式(2)中y(t)的包络信号可由下式表示：

(3)

式中：Y(t)为y(t)的包络信号。

2 太阳轮振动信号加窗平均技术

2.1太阳轮故障振动分析

行星齿轮传动中，若太阳轮发生齿根裂纹等故障，传感器的位置与齿轮故障源啮合点的相对位置会随着振动传递路径的远近而具有时变性。其故障齿啮合振源产生的振动信号主要通过行星轮直接传递至齿圈，然后通过箱体传递至传感器，传递路径距离最短(图1所示)，且界面较少，信号衰减最少[4]，成为本文振动分析的主要考虑之一。

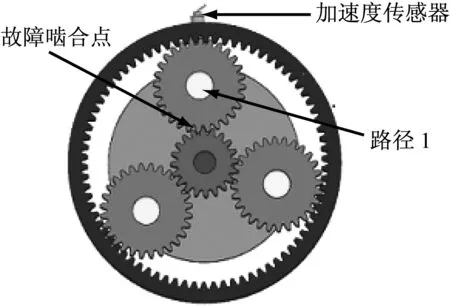
图1 传输路径

由行星齿轮传动理论[4]，啮合频率fm的关系式：

fm=Nafc=Np(fc+fp)=Ns(fs-fc)

(4)

式中：fm代表啮合频率;fs为太阳轮旋转频率;fc为行星架旋转频率;fp为行星轮旋转频率;Ns，Na，Np分别表示太阳轮、齿圈、行星轮的齿数。

由式(4)整理得，行星架与太阳轮传动比ics为：

(5)

若Ns=28，Na=71(对应试验)，则由式(5)可得ics=28/99。

由太阳轮故障点与行星轮的啮合位置与传感器最近时开始计算，如图(1)所示。假设只有一个行星轮的条件下，为保证太阳轮和行星架转的圈数满足最小正整数关系，太阳轮需旋转99圈，行星架恰好旋转最小正整数圈28圈，同时行星轮也围绕齿圈转过28圈(行星架自转一圈相当于一个行星轮围绕齿圈转过一圈)。如果行星轮数量为N个，则太阳轮旋转99圈期间有N乘以28个行星轮通过齿圈顶端的传感器。若使太阳轮故障点与行星轮的啮合位置与传感器最近(图1所示)。需要太阳轮同样达到此位置，必须旋转过正整数圈。而行星轮只需其中一个在太阳轮旋转到(图1所示)齿圈最顶端即可。由上面分析可知，当太阳轮转过99圈，此时，恰好同一故障点第二次到达(图1所示)位置，传感器所拾取故障对应振动信号幅值也同时再次达到最大。

2.2加窗分离技术

若将振动传感器安装在固定齿圈上，太阳轮故障齿与不同行星轮轮齿(因行星齿轮传动系统至少一个行星轮)啮合产生故障振动信号相对传感器的相对位置将随太阳轮的自转而发生变化，因而在不同时刻采集的振动信号具有时变性。为能从中提取有用信号，并且抑制其强度被削弱，本文采用窗函数提取方法。相关研究表明Tukey窗效果较好，Tukey窗的详细原理可参见Samuel Conroy等的结论。

McFadden提出的分段加窗平均法(图2所示)，其可减小振动传递路径变化对信号的影响。其原理可以解释为，对太阳轮每自转一转用窗函数(Tukey窗)截取一片段信号。由上述太阳轮振动分析可知，以相邻两次传感器拾取振动信号幅值最大为间隔，作为一个平均整周期。在此期间，太阳轮将转过N1圈。

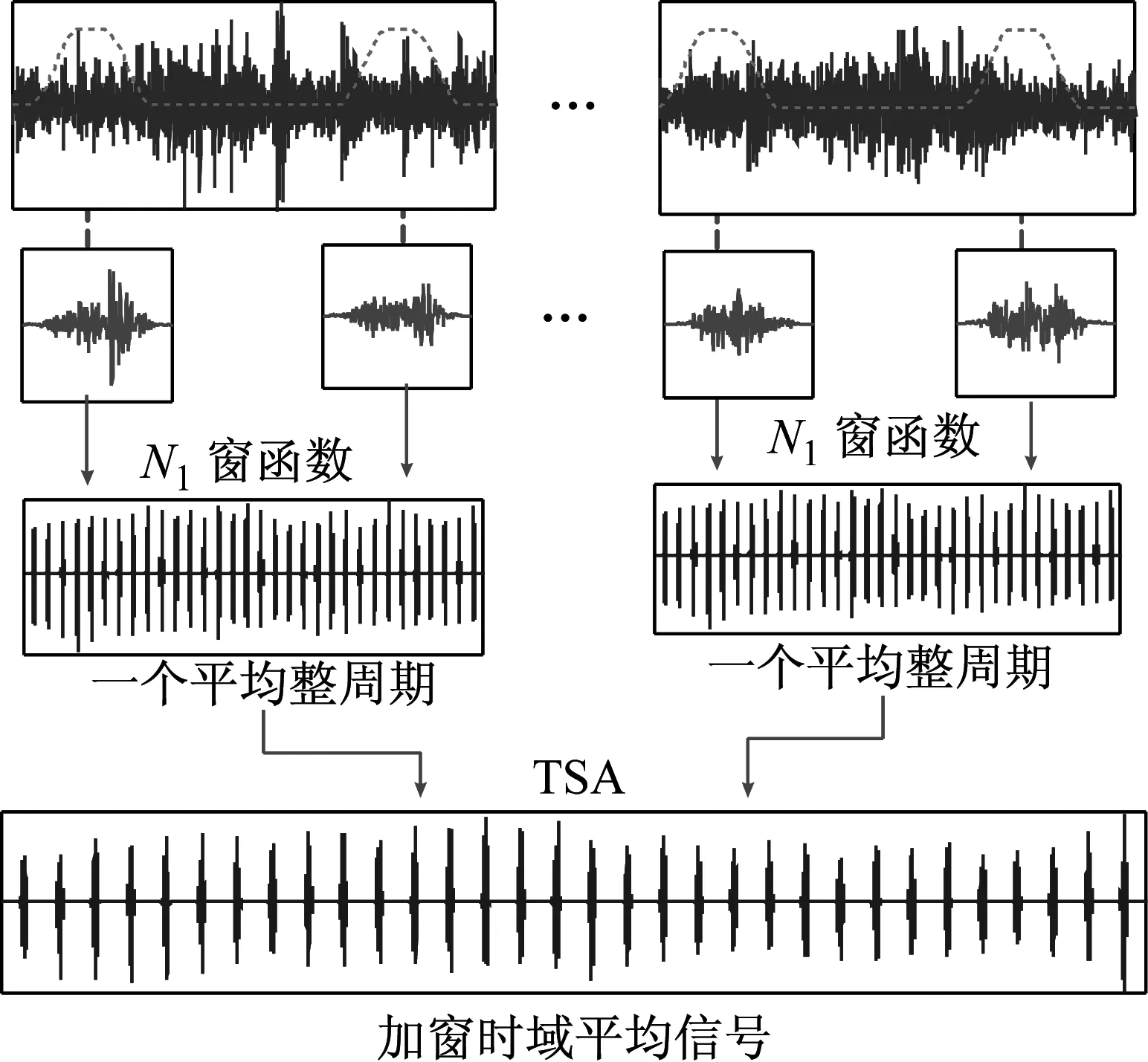
图2 窗函数分离太阳轮振动信号同步平均过程

3 太阳轮振动信号包络角域加窗同步平均技术

3.1阶比跟踪简介

计算阶比跟踪(COT)是一种通过对振动信号进行等角度采样将其转换为准平稳角域信号以减少或者抑制转速波动的影响，是变速工况条件下旋转机械振动的有效分析工具。

COT在实现上，首先对原始测试振动信号和参考轴的转速脉冲进行恒定采样率的同步采样，再以转速脉冲作为键相时标对采集到的振动信号进行等角度重采样，转换为准平稳角域信号，并对其采用基于FFT的信号处理算法可获取阶比谱等特征信息，并克服由于转速波动造成的频率模糊现象。COT的详细原理可参见文献[14]。

3.2包络角域加窗同步平均技术

常规的平均方法只是针对时域或角域振动信号进行。本文研究中结合包络分析、加窗同步平均以及计算阶比跟踪的优势，提出一种适合弱特征信号解调、时变传递路径及变速工况的包络角域加窗同步平均技术。其实现原理如图(2)所示。主要分析步骤包括：

(1)Tukey窗函数对拾取的原始测试故障振动信号进行加窗处理，获取加窗振动信号y(t)。

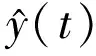
(3)等角度采样时标的获取。利用计算阶比跟踪算法获得等角度采样时标Tn。

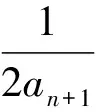
(6)

式中：an，an+1，an+2是对应连续三个脉冲时刻的常系数；θ为等角度采样间隔。

(3)复包络角域加窗信号获取。由第(2)步得到的复包络加窗信号Y(t)，在第(3)步计算出的等角度采样时标Tn上进行线性插值运算，获取复包络角度加窗信号Y(Tn)。

(4)包络角域加窗同步平均。对复包络角域加窗信号的实部和虚部分别进行同步平均，得到复包络角域加窗同步平均信号。

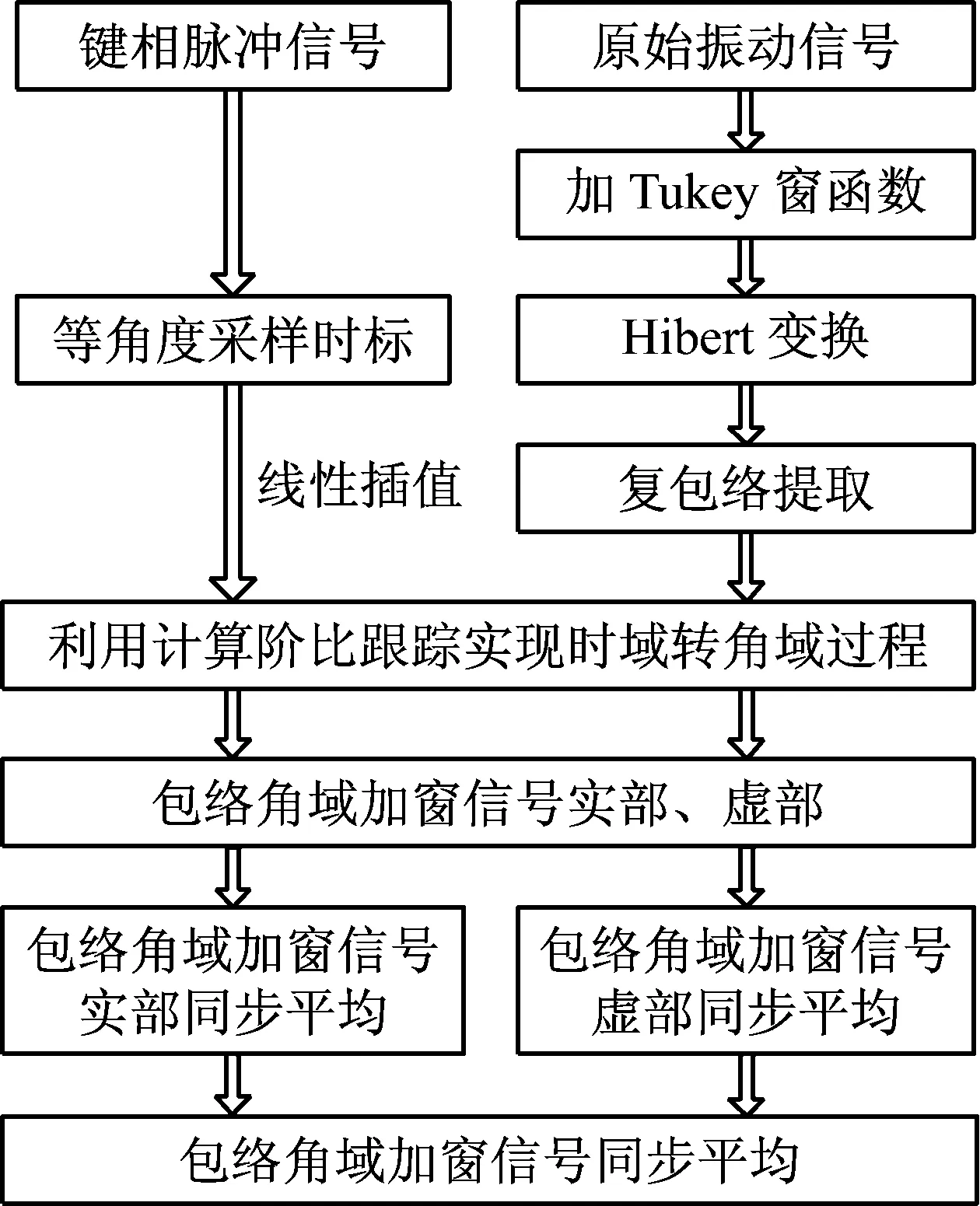
图3 包络角域加窗同步平均原理图

Fig.3 Schematic of the envelop angle synchronous average with window function

图4 行星齿轮传动实验台

(5)太阳轮故障特征分析。对获取的复包络角域加窗信号进行FFT频谱分析得到阶比谱，并与太阳轮轮齿故障理论阶比特征进行对比，实现对太阳轮故障特征的提取。

4 测试试验分析

4.1实验说明

本实验数据采集于行星齿轮传动故障诊断综合实验台，实验台见图(4)，行星齿轮箱参数(见表1)。为了模拟行星齿轮箱太阳轮局部故障，在太阳轮其中一个轮齿上加工了一个齿根裂纹(研究中采用电火花加工方法加工出一个深度约为5 mm的齿根裂纹故障)，如图(5)所示。试验过程中，数据采集设备为NI USB9234采集卡，采样频为51.2 kHz；在行星齿轮箱上安装了加速度传感器，加速度传感器型号为DH112(灵敏度5.20 pC/g)，布置如图(4)中Ⅰ、Ⅱ、Ⅲ处；在输出轴处安装了脉冲传感器，采集输出轴转速脉冲，转速脉冲采用DH904电涡流传感器(灵敏度为2.5 V/mm)获取，见图(4)中2处；通过调速器设置转速为1 000 r/min，实际太阳轮轴的转速约为1 000 r/min(由于电流、负载等原因存在轻微波动)。采集太阳轮轮齿故障的行星齿轮箱振动信号。

表1 行星齿轮箱参数

由式(4)可计算出行星轮相对于行星架的转频fpc，太阳轮相对于行星架的转频fsc。

fpc=fp+fc=fc(Na/Np)

(7)

fsc=fs-fc=fc(Na/Ns)

(8)

代入太阳轮轴转速ns=1 000 r/min，由式(7)、(8)以及行星齿轮箱参数(见表1)可计算出行星齿轮箱的特征频率(见表2)。

表2 行星齿轮箱特征频率

若太阳轮的某个轮齿存在局部损伤，其相对行星架旋转，故障轮齿与行星轮啮合振源会产生冲击。由式(8)太阳轮局部故障特征频率为：

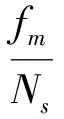
(9)

式中：fs1为太阳轮故障特征频率。由阶比的定义公式：

(10)

式中:f为振动信号频率(单位：Hz);R为对应参考轴转速(单位：r/min);l表示阶比。由式(10)可计算出行星齿轮箱的阶比(见表3)，同时由式(9)则太阳轮局部故障特征阶比为：

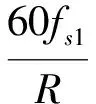
l== (11)

图5 齿根裂纹太阳轮

代入fs1=11.952 9 Hz，由式(11)可得ls1=0.717 2×。

4.2太阳轮振动信号故障特征提取

图(6)为行星齿轮箱采集的时域振动信号，其中图6(a)为原始测试振动信号，图6(b)为加窗振动信号，6(c)、(d)分别是转速脉冲、转速曲线。

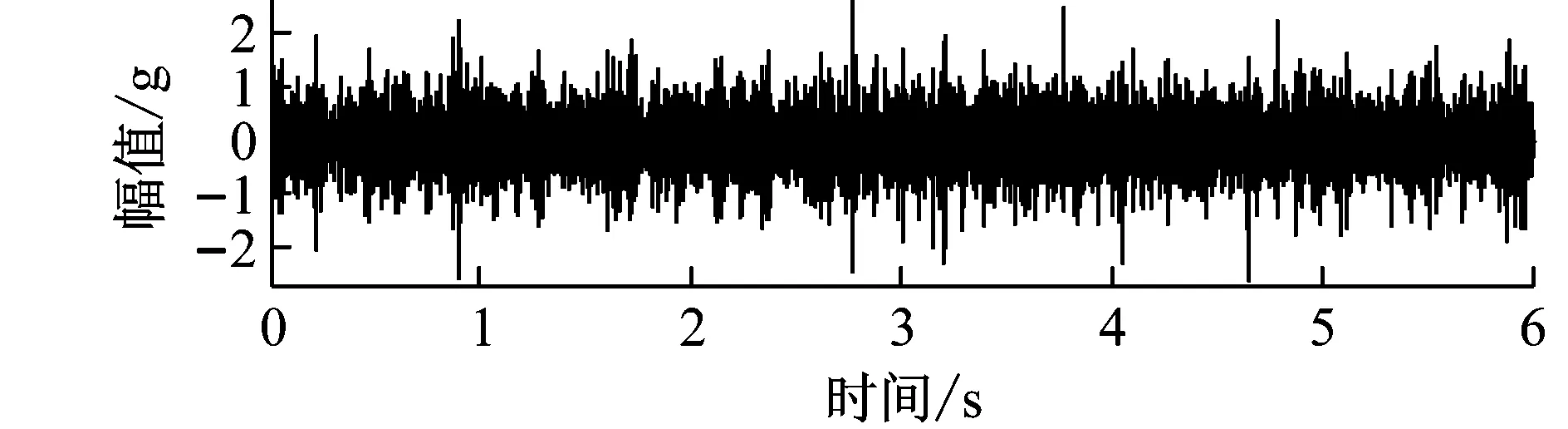
(a) 原始测试振动信号

(b)加窗振动信号

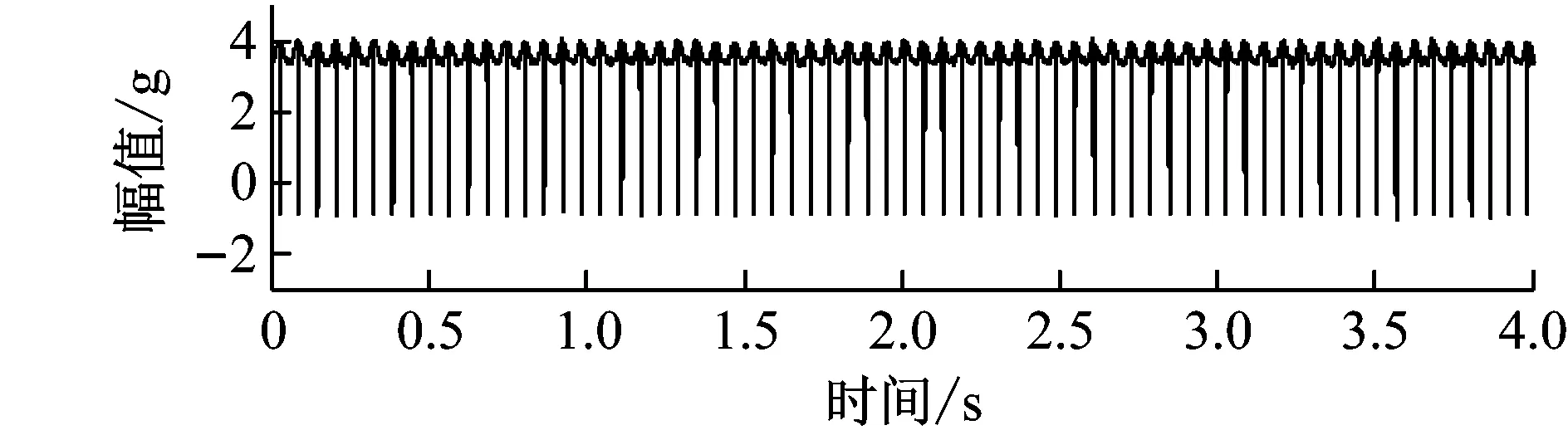
(c) 转速脉冲

(d) 转速曲线

Fig.6 Raw vibration signal, Envelop vibration signal, Tacho pulse and Speed curve

按图(2)的步骤，对获取的复包络时域加窗信号，选取输入轴为参考轴，利用计算阶比跟踪使时域复包络加窗信号转换到角域，再进行角域平均，得到图7所示的阶比谱。图6(a)出现明显振幅调制的成分，并且调幅后产生多种大小不同的振幅，这些调幅成分具有明显的周期性。图7(a)角域加窗同步平均阶比谱，图7(b) 为包络角域加窗同步平均阶比谱。对比图7(a)，7(b)可发现振动信号采用本文提出包络角域加窗同步平均方法干扰阶比分量对应的谱线被明显抑制，而与太阳轮故障特征阶比分量(边带)清晰可见，见图7(b)。由于行星齿轮箱的故障信号随传输路径而不断变化，边带成份非常复杂，试验发现在阶比谱的转频及其谐波分量周围存在由其齿根裂纹故障引起的调制边带分量，故障特征阶比频率是太阳轮旋转阶比ls(1×、2×、3×、4×、5×，对应图7(b))的调制边带成份，见图7(b)标注，例如，太阳轮1×左侧边带阶比谱线:0.282 8×，其与1×谱线间隔正好为太阳轮局部故障对应阶比0.717 2，太阳轮1×右侧阶比边带阶比谱线:1.717 2×，其与1×谱线间隔同样正好为太阳轮局部故障对应阶比0.717 2×；同理，太阳轮2×左侧边带阶比谱线:1.282 8×，其与2×谱线间隔正好为太阳轮局部故障对应阶比0.717 2，太阳轮2×右侧阶比边带阶比谱线:2.717 2×，其与2×谱线间隔同样正好为太阳轮局部故障对应阶比0.717 2×；其它，3×、4×、5×谱线边带显示的太阳轮局部故障对应的特征阶比谱线可以此类推，见图7(b)。

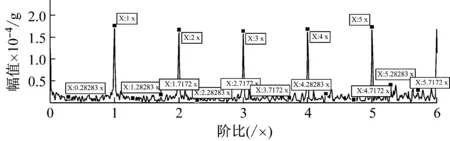
(a) 角域加窗同步平均阶比谱

(b) 包络角域加窗同步平均阶比谱

Fig.7 Order spectrum of angular and envelope domain synchronous average of vibration signal with window function

5 结 论

本文主要利用包络分析在弱特征信号提取方面的优势，可有效提取太阳轮早期故障因经过较为复杂传输路径的衰减，导致故障响应微弱振动信号，同时包络分析、加窗同步平均以及计算阶比跟踪相结合的基础上进一步提出包络角域加窗同步平均技术。其能够有效对太阳轮故障弱特征信号进行高信噪比解调，同时可以抑制或者减少由于时变传输路径、转速、载荷波动等造成的影响。试验表明，本方法可有效实现对行星齿轮箱太阳轮故障弱特征信号准确提取。

[1] LEI Y, LIN J, ZUO M J, et al. Condition monitoring and fault diagnosis of planetary gearboxes: a review[J]. Measurement, 2014, 48: 292-305.

[2] BRAUN S. The synchronous (time domain) average revisited [J]. Mechanical Systems & Signal Processing, 2011, 25(4):1087-1102.

[3] MCFADDEN P D. A technique for calculating the time domain averages of the vibration of the individual planet gears and the sun gear in an epicyclic gearbox[J]. Journal of Sound and Vibration, 1991, 144(1): 163-172.

[4] LEWICKI D G, SAMUEL P D, CONROY J K, et al. Planetary transmission diagnostics[J]. NASA CR, 2004, 213068.

[5] LEWICKI D G, LABERGE K E, EHINGER R T, et al. Planetary gearbox fault detection using vibration separation techniques[R]. 2011.

[6] HOOD A, LABERGE K, LEWICKI D, et al. Vibration based sun gear damage detection[C]//ASME 2013 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. American Society of Mechanical Engineers, 2013: V005T11A033-V005T11A033.

[7] LEI Y, HAN D, LIN J, et al. Planetary gearbox fault diagnosis using an adaptive stochastic resonance method[J]. Mechanical Systems & Signal Processing, 2013, 38(1):113-124.

[8] FENG Z, LIN X, ZUO M J. Joint amplitude and frequency demodulation analysis based onintrinsic time-scale decomposition for planetary gearbox fault diagnosis[J]. Mechanical Systems and Signal Processing, 2016, 72/73: 223-240.

[9] 冯志鹏,赵镭镭,褚福磊. 行星齿轮箱齿轮局部故障振动频谱特征[J]. 中国电机工程学报,2013,33(5):119-127.

FENG Zhipeng, ZHAO Leilei，CHU Fulei. Vibration spectral characteristics of localized gear fault of planetary gearboxes[J].China CSEE, 2013,33(5): 119-127.

[10] 冯志鹏，褚福磊. 行星齿轮箱故障诊断的频率解调分析方法[J]. 中国电机工程学报, 2013,33(11): 112-117.

FENG Zhipeng, CHU Fulei. Frequency demodulation analysis method for fault diagnosis of planetary gearboxes [J]. Proceedings of the CSEE, 2013,33(11)：112-117.

[11] FYFE K R, MUNCK E. Analysis of computed order tracking. Mech Syst Sig Proces[J]. Mechanical Systems & Signal Processing, 1997, 11(2):187-205.

[12] GUO Y, LIU T W, NA J, et al. Envelope order tracking for fault detection in rolling element bearings[J]. Journal of Sound & Vibration, 2012, 331(25):5644-5654.

[13] 冯志鹏, 秦嗣峰. 基于 Hilbert 振动分解和高阶能量算子的行星齿轮箱故障诊断研究[J]. 振动与冲击, 2016, 35(5):47-54.

FENG Zhipeng, QIN Sifeng. Planetary gearbox fault diagnosis based on Hilbert vibration decomposition and higher order differential energy operator [J].Vibration and Shock, 2016, 35(5): 47-54.

[14] 王况, 王科盛, 左明健,等. 基于阶次分析技术的行星齿轮箱非平稳振动信号分析[J]. 振动与冲击, 2016, 35(5):140-145.

WANG Kuang, WANG Kesheng, ZUO Mingjian, et al. Fault diagnosis of a planetary gearbox based on order tracking [J]. Journal of Vibration and Shock, 2016, 35(5): 140-145.

Featureextractionoffaultysungearsignalsbasedontheenvelopewindowedsynchronousaverageinangledomain

WANGZhile,GUOYu,WUXing

(Faculty of Mechanical and Electrical Engineering, Key Lab. of Vib. & Noise under Ministry of Education of Yunnan Province, Kunming University of Science and Technology, Kunming 650500, China)

Planetary gearboxes are widely used in wind turbines and other large machinery. Due to the non-stationary characteristic of signals, the modulation as well as the complexity and time-varying property of its transmission path, the fault response signals, usually quite weak, are easily submerged in the strong background noise. By the combined use of the envelope analysis, windowed synchronous average and computed order tracking, an envelope windowed synchronous average in angle domain, suitable for the weak feature signals demodulation, time-varying transmission paths and varying-speed working conditions was proposed. In the method, fault vibration signals were dealt with by using the tukey window function, the Hilbert transform (HT) was used to obtain the complex envelope signals and the complex envelope signals in time domain were sampled at constant angle increments according to the computed order tracking (COT), which converts the non-stationary signals in the time domain into the stationary ones in the angle domain. Then, the angle-domain signals were processed by the signal synchronous average (SA). Experimental tests were conducted to verify the validity of the proposed method.

planetary gearbox; envelope analysis; windowed synchronous average; computed order tracking

TH133.33

A

10.13465/j.cnki.jvs.2017.21.010

国家自然科学基金(51675251)

2016-06-02 修改稿收到日期：2016-08-30

王志乐 男,硕士生,1990年5月生

郭瑜 男,教授,博士生导师,1971年12月生