考虑附加质量的旋转柔性梁动态可靠性分析

靳红玲， 王 威， 冯 涛， 郭成洋， 陈 军

(西北农林科技大学 机械与电子工程学院，陕西 杨凌 712100)

考虑附加质量的旋转柔性梁动态可靠性分析

靳红玲， 王 威， 冯 涛， 郭成洋， 陈 军

(西北农林科技大学 机械与电子工程学院，陕西 杨凌 712100)

在带有附加质量的旋转柔性梁系统动态可靠性分析中，为了提高其计算精度和计算效率，提出了一种基于单项式容积法(Monomial Cubature Rules,MCR)的随机响应面法(Stochastic Response Surface Method,SRSM)。该方法利用MCR的积分点作为样本点，并以此生成柔性梁系统动态响应的小样本对，基于这些样本对和SRSM回归理论，建立柔性梁系统动态响应可靠度隐式功能函数的代理模型，使用该代理模型对柔性梁系统进行动态响应可靠性分析。通过与传统的蒙特卡洛(Monte Carlo,MC)法和改进的概率配点法(Efficient Collocation Method,ECM)比较，表明了该方法在柔性梁系统动态响应可靠性分析中的高效率和高精度。在取相同变异系数的条件下，柔性梁截面宽度参数的分散性对系统动态响应的可靠性影响较大。

柔性梁;附加质量;随机响应面法;单项式容积法;动态可靠性

随着现代机械向高速、轻质、高精度的方向发展，旋转柔性机械臂的动力学问题越来越受到关注[1-3]。旋转柔性机械臂通常可以抽象为旋转柔性梁，其动力学模型是复杂的时变微分代数方程，致使在进行动态可靠性分析时，功能函数很难以解析形式表达。理论上，MC(Monte Carlo)法利用随机抽样和概率统计方法计算结构的随机响应量，是一种比较直接、精确的方法。但对于小概率失效事件，MC需要大量的样本点才能保证计算精度，计算成本较高[4]。

SRSM(Stochastic Response Surface Method)使用Hermit多项式拟合输出响应与输入参数之间的复杂隐函数关系，建立功能函数的代理模型，能够快速得到系统动态响应的可靠度，因而在可靠度领域得到广泛的应用[5-8]。然而，SRSM的计算效率和精度取决于配点的选取，传统的概率配点法(Probabilistic Collection Method,PCM)[9]和改进的概率配点法(Efficient Collocation Method,ECM)[10]在高维系统中由于局部抽样可能会产生很大误差，甚至严重失真[11]。为了提高SRSM的计算精度和计算效率，Li等[12]初步提出了采用基于线性无关原则选取概率配点的思想，并研究了该方法在地下水溶质运移不确定性分析中的应用。杨绿峰等在文献[12]的基础上，引入逐步回归分析剔除响应面展开项中的次要项，从而大幅减少了展开式中的待定系数。蒋水华等[13]系统地研究了SRSM采用线性无关原则选取概率配点的优越性，并比较了基于回归方法和基于线性无关原则选取概率配点的优缺点。

为解决PCM和ECM局部抽样存在的问题，本文采用基于单项式容积法(Monomial Cubature Rules,MCR)的SRSM(简写为MCR-SRSM)建立柔性梁系统动态响应可靠度分析的代理模型，并将该方法应用于考虑附加质量的旋转柔性梁的动态响应可靠性分析。

1 单项式容积法

旋转柔性梁动态响应是时间t的函数，采用基于回归分析的SRSM，其动态响应的隐式功能函数g′也是时间的函数，采用p次的Hermite多项式展开表示为

(1)

式(1)即为隐式功能函数g′的代理模型。式中，混沌多项式展开式的待定系数构成矢量a(t)=[a1(t),a2(t),…aN(t)]；Hk(ξ)为Hermite多项式，ξ=(ξ1,…,ξn)是n维彼此相互独立的、且服从标准正态分布的随机向量，n是随机变量的个数；N为待定系数的个数，其表达式为

(2)

式中，p为Hermite多项式展开的阶次。

在SRSM的应用过程中，最主要的工作就是如何选取配点以求解式中的待定系数矢量a(t)。Tatang等提出的PCM是在高一阶Hermite多项式根的组合(p+1)n个样本点中选取N个点作为配点求解待定系数；为了避免PCM可能产生的不稳定现象，Isukapalli提出了ECM，即将配点数选取为待定系数个数的2倍以提高计算精度。但两种方法在高维情况下，显然有(p+1)nN，如何从(p+1)n个样本点中选取N个作配点仍是一个不确定问题，不同的积分点组合会产生不同的计算结果，将直接影响代理模型的精度。

本文采用的MCR是高效的多重数值积分方法，当给定数值积分的精度后，MCR生成数量最少的积分点。Stroud[14]指出MCR生成精度为2p+1的n维的积分点个数通常很接近p次的PC系数的个数这个下限值，因此全部的积分点可以作为配点，且计算量小。该方法已成功应用于容差分析[15]、优化设计[16]和随机动力学分析[17]。

以下给出本文采用的部分5阶和7阶精度MCR公式(分别对应于2次和3次Hermite多项式展开)，详见Stroud的结论。

1) 公式Ⅰ

具有5阶精度，对于n(2≤n≤7)维变量，积分点个数为s=n2+n+2。当n≥4时，它是已知5阶精度公式中需要的配置点个数最少，有

I(f)≈A[f(η,η,η,…,η)+f(-η,-η,-η,…,-η)]+

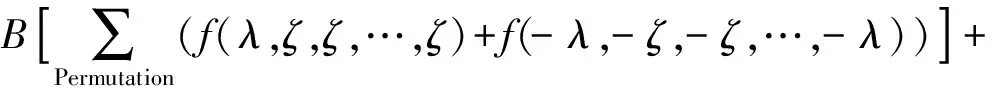
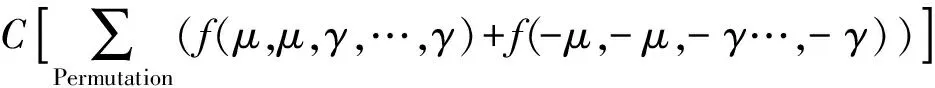
(3)

式中，μ,γ,η,λ,ζ,A,B,C分别为配置点和权系数。其中，μ,γ,η由以下关系式确定：

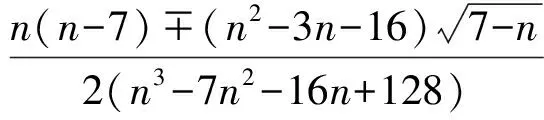
λ=1.328 947。

2) 公式Ⅱ

具有7阶精度，对于n(n≥3)维变量，积分点个数为s=2n+1+4n2。虽然积分点数随维数的增加而增加较快，但是该公式的权系数都为正数，所以对于高维问题，数值计算的稳定性很好[18]。该公式的表达式如下：

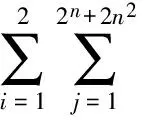
(4)

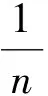
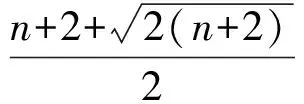
2 随机动力学模型

图1所示为在水平面内作大范围运动规律为已知的柔性悬臂梁，θ为大范围运动的角位移。设该梁为均质等截面Euler-Bernoulli梁，其截面弹性轴与中性轴共线，忽略系统的重力。中心刚体半径rA，梁的自由端附有集中质量m，梁的横截面宽度y、高度z、长L，体积密度ρ、弹性模量E。XOY为系统惯性坐标系，为固结于梁上的浮动坐标系。

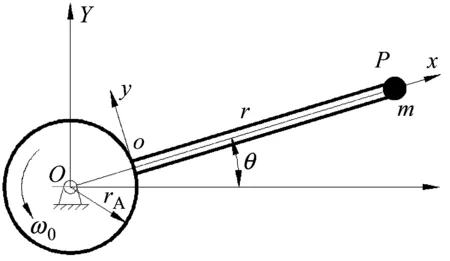
图1 考虑附加质量的柔性悬臂梁系统

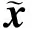
(5)

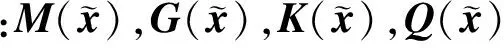
3 基于代理模型的可靠度分析

旋转柔性梁的动力学模型是复杂的时变微分代数方程，其动态响应可靠度分析时的函数为隐式功能函数。本文采用代理模型g代替隐式功能函数g′，进行柔性梁动态可靠度分析。

3.1动态可靠性基本理论

(6)

相应的，柔性梁末端动态变形响应可靠度可以定义为：运动时域T内，动态响应在允许值范围内的概率，即可靠度R可表示为

R(t)=P(g′≥0)

(7)

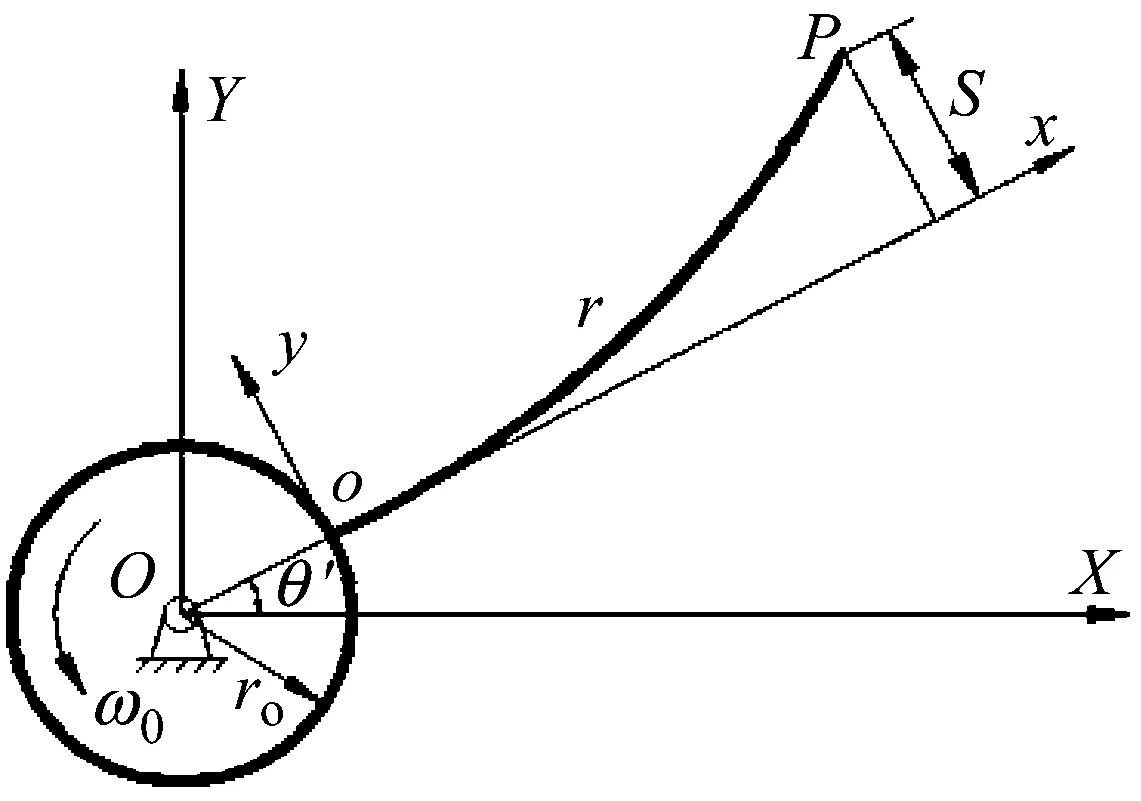
图2 柔性梁的变形示意图

3.2动态可靠度分析的MCR-SRSM法

基于代理模型g进行动态可靠度分析，关键是求解式(1)的待定系数矢量a(t)。本文采用MCR-SRSM法求解a(t)，将其代入式(1)得到代理模型中变量和响应的函数关系，具体方法如下：

3.2.1 动态响应许用值的确定

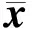
(8)

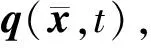
3.2.2 动态响应的小样本对

(9)

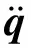
(10)

3.2.3 动态响应可靠度分析的代理模型

为求解代理模型中的待定系数矩阵，将小样本对{(ξ1,g1),…,(ξj,gj),…,(ξs,gs)}代入式(1)，得到一组以a(t)为未知数的方程组，再利用SRSM回归分析确定出对应于不同时刻t的待定系数矩阵a(t)，把a(t)代入式(1)得到代理模型g(ξ,t)的表达式。

对于a(t)已知的代理模型g(ξ,t)，利用MC对ξ=(ξ1,…,ξn)进行r次大批量抽样ξi,i=1,…,r，求出对应于时刻t的r个功能函数值{g1,…,gr}，根据式(7)对r个功能函数值进行统计分析得到动态响应随时间的可靠度R(t)。

综上所述，基于代理模型的可靠度分析求解步骤如下：

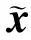
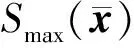
3) 将小样本对{(ξ1,g1),…,(ξj,gj),…,(ξs,gs)}中的ξj作为输入，gj作为输出代入式(1)，利用SRSM回归分析确定待定系数矩阵a(t)，将a(t)代入式(1)得到代理模型g(ξ,t)的表达式；

4) 利用MC对代理模型进行大批量抽样统计分析得到动态响应随时间的可靠度。

具体的柔性梁动态响应可靠度求解流程图见图3，其中k为时域上的积分点数。

图3 基于MCR-SRSM动态可靠性求解流程图

4 实 例

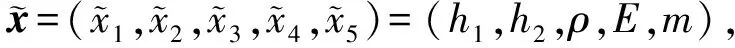
柔性悬臂梁由静止开始作大范围旋转运动，角速度规律为

式中:T为达到恒定转速之前的加速时间，取T=15 s;ω0为t>T时的恒定转速，取ω0=4 rad/s。

文中按公式I和II采用模拟次数分别为s=52+5+2=32和s=25+1+4×52=164的五阶MCR(简写为MCR-5th)和七阶MCR(简写为MCR-7th)，以及模拟次数为s=2N=2(5+3)!/(5!3!)=112的三次ECM(简写为ECM-3rd)求解该旋转柔性梁末端的变形响应的可靠度。

图4 梁末端的变形响应

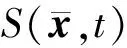
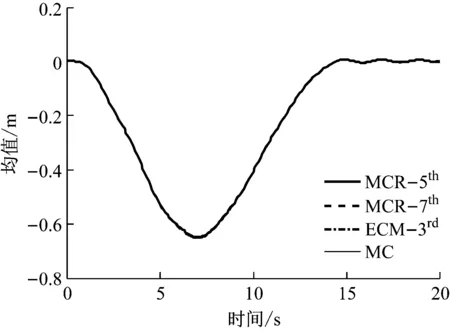
(a)

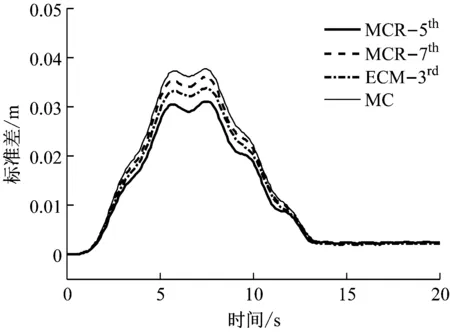
(b)

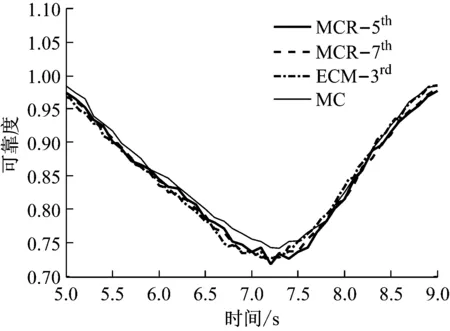
图6 梁末端动态响应的可靠度曲线(γall=0.05)

图7 不同随机变量组合对系统可靠度的影响曲线

Fig.7 Reliability curve with different random variables impacting on the system

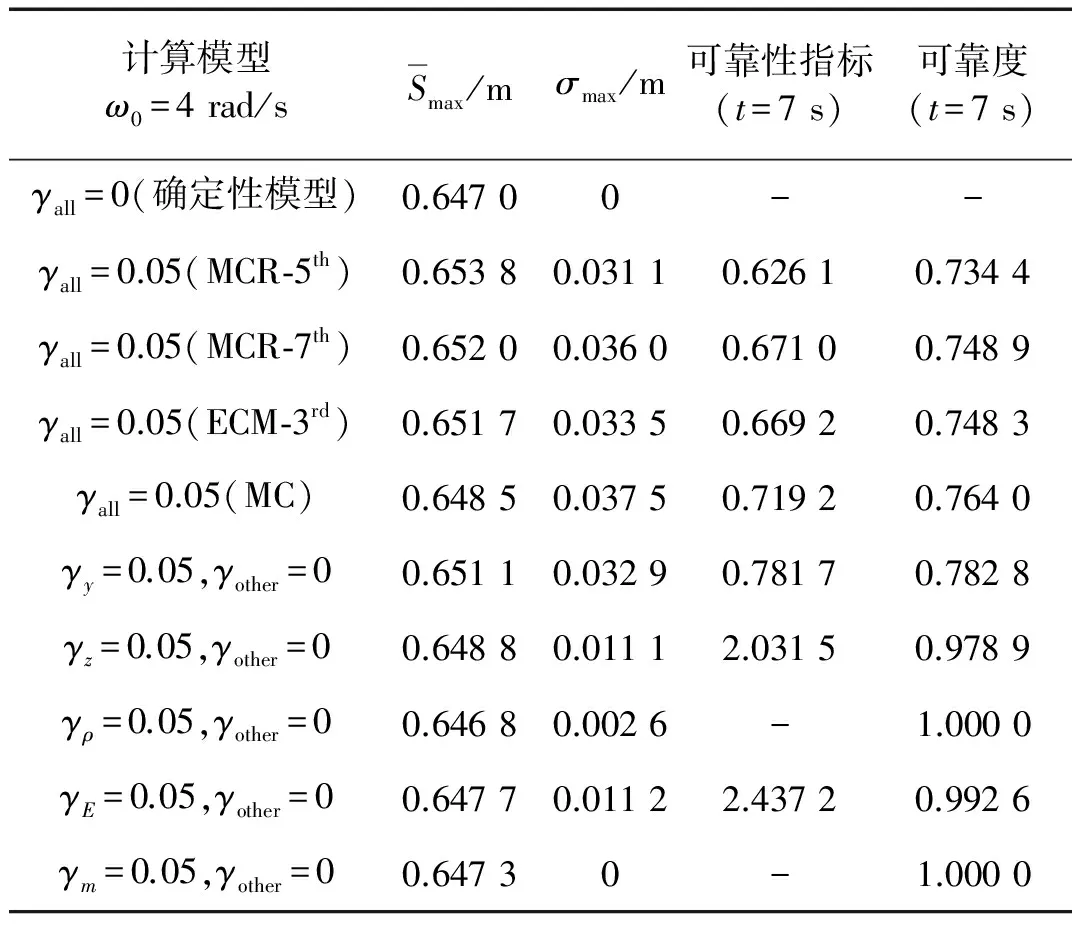
表1不同随机变量组合对系统可靠度的影响

Tab.1Differentrandomvariablesimpactingonthereliabilityofthesystem

计算模型ω0=4rad/sSmax/mσmax/m可靠性指标(t=7s)可靠度(t=7s)γall=0(确定性模型)0．64700--γall=0．05(MCR⁃5th)0．65380．03110．62610．7344γall=0．05(MCR⁃7th)0．65200．03600．67100．7489γall=0．05(ECM⁃3rd)0．65170．03350．66920．7483γall=0．05(MC)0．64850．03750．71920．7640γy=0．05，γother=00．65110．03290．78170．7828γz=0．05，γother=00．64880．01112．03150．9789γρ=0．05，γother=00．64680．0026-1．0000γE=0．05，γother=00．64770．01122．43720．9926γm=0．05，γother=00．64730-1．0000

5 结 论

本文采用MCR的积分点作为SRSM回归分析的配点建立可靠度功能函数的代理模型，对旋转柔性梁系统的动态响应可靠性进行分析，得出以下结论：

(1) MCR只生成少量的积分点，可全部作为SRSM回归分析时的配点，计算量小；同时解决了高维情况下ECM局部抽样存在的问题，使求解功能函数的代理模型更加稳健。

(2) 相对于MC，利用本文MCR-SRSM方法求解旋转柔性梁动态响应的可靠度，显著地减少了模拟次数，提高了计算效率，具有较高的计算精度。

(3) 各参数的随机性对柔性体的动态变形响应可靠度的影响不可忽略，故欲增强系统的可靠性，应首先降低对可靠性影响显著的参数分散性。

[1] 戎保, 芮筱亭, 王国平, 等. 多体系统动力学研究进展 [J]. 振动与冲击, 2011, 30(7): 178-187.

RONG Bao，RUI Xiaoting，WANG Guoping，et al. Developments of studies on multibody system dynamics [J]. Journal of Vibration and Shock, 2011, 30(7): 178-187.

[2] 杜超凡, 章定国, 洪嘉振, 等. 径向基点插值法在旋转柔性梁动力学中的应用 [J]. 力学学报, 2015, 47(2): 279-288.

DU Chaofan, ZHANG Dingguo, HONG Jiazhen, et al. A meshfree method based on radial point interpolation method for the dynamic analysis of rotating flexible beams[J]. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(2): 279-288.

[3] 王建明, 刘又午, 洪嘉振. 大范围刚体运动对柔性梁模态形函数的影响分析 [J]. 中国机械工程, 2000, 11(6): 640-643.

WANG Jianming, LIU Youwu, HONG Jiazhen. Analysis on the mode shapes of flexible beams affected by large overall motion [J]. China Mechanical Engineering, 2000, 11(6): 640-643.

[4] 杨绿峰, 杨显峰, 余波, 等. 基于逐步回归分析的随机响应面法 [J]. 计算力学学报, 2013, 30(1): 88-93.

YANG Lufeng, YANG Xianfeng, YU Bo, et al. Improved stochastic response surface method based on stepwise regression analysis[J]. Chinese Journal of Computational Mechanics, 2013, 30(1): 88-93.

[5] JI Y. Fuzzy reliability analysis of nonlinear structural system based on stochastic response surface method [J]. Advanced Materials Research, 2014, 912/913/914: 1268-1271.

[6] ZHAO Q H, CHEN X K, MA Z D, et al. Reliability-based topology optimization using stochastic response surface method with sparse grid design [J]. Mathematical Problems in Engineering, 2015(2015):487686.

[7] 赵宽, 陈建军, 曹鸿钧, 等. 随机参数双连杆柔性机械臂的可靠性分析 [J]. 工程力学, 2015, 32(2): 214-220.

ZHAO Kuan, CHEN Jianjun, CAO Hongjun, et al. Reliability analysis on two-link flexible robot manipulator with random parameters [J]. Engineering Mechanics, 2015, 32(2): 214-220.

[8] KIM N H, KIM Y J. Safety envelope for load tolerance and its application to fatigue reliability design [J]. Journal of Mechanical Design, 2006, 128(4): 919-927.

[9] TATANG M A, PAN W, PRINN R G, et al. An efficient method for parametric uncertainty analysis of numerical geophysical models [J]. Journal of Geophysical Research Atmospheres, 1997, 102(18): 21925-21932.

[10] ISUKAPALLI S S, Roy A, GEORGOPOULOS P G. Efficient sensitivity/uncertainty analysis using the combined stochastic response surface method and automated differentiation: application to environmental and biological systems [J]. Risk Analysis, 2000, 20(5): 591-602.

[11] 胡冉, 李典庆, 周创兵, 等. 基于随机响应面法的结构可靠度分析[J]. 工程力学, 2010, 27(9): 192-200.

HU Ran, LI Dianqing, ZHOU Chuangbing, et al. Structural reliability analysis using stochastic response surface method [J]. Engineering Mechanics, 2010, 27(9): 192-200.

[12] LI D Q, CHEN Y F, LU W B, et al. Stochastic response surface method for reliability analysis of rock slopes involving correlated non-normal variables [J]. Computers & Geotechnics, 2011, 38(1): 58-68.

[13] 蒋水华, 李典庆, 周创兵. 随机响应面法最优概率配点数目分析 [J]. 计算力学学报, 2012, 29(3): 345-351.

JIANG Shuihua, LI Dianqing, ZHOU Chuangbing. Optimal probabilistic collocation points for stochastic response surface method [J]. Chinese Journal of Computational Mechanics, 2012, 29(3): 345-351.

[14] STROUD A H. Approximate calculation of multiple integrals [M]. N J: Prentice-Hall, Englewood Cliffs, 1971．

[15] 韦东来, 崔振山, 陈军. 混沌多项式新求解及其在板料成形性容差预测中的应用 [J]. 机械工程学报, 2009, 45(8): 261-265.

WEI Donglai, CUI Zhenshan, CHEN Jun. New solution for polynomial chaos expansion and application in tolerance prediction for stamping process[J]. Jounal of Mechanical Engineering, 2009, 45(8): 261-265.

[16] WEI D, CUI Z, CHEN J. Robust optimization based on a polynomial expansion of chaos constructed with integration point rules [J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2009, 223(5): 1263-1272.

[17] 靳红玲, 陈建军, 赵宽, 等. 空间柔性梁的随机动力学分析 [J]. 西安电子科技大学学报, 2015, 42(4): 47-52.

JIN Hongling, CHEN Jianjun, ZHAO Kuan et al. Stochastic dynamic analysis of spatial flexible beam [J]. Journal of Xidian University, 2015, 42(4): 47-52.

[18] 韦东来. 汽车覆盖件成形工艺的稳健优化与容差分析 [D]. 上海: 上海交通大学, 2009.

[19] 靳红玲, 陈建军, 郭康权. 考虑附加质量的旋转柔性梁的随机动力学分析 [J]. 振动工程学报, 2015, 28(6): 960-965.

JIN Hongling, CHEN Jianjun, GUO Kangquan. Stochastic dynamic analysis of spatial flexible beam with tip mass [J]. Journal of Vibration Engineering, 2015, 28(6): 960-965.

Dynamicreliabilityanalysisofarotatingflexiblebeamwithtipmass

JINHongling,WANGWei,FENGTao,GUOChengyang,CHENJun

(School of Mechano-electronic Engineering, Northwest A&F University, Yangling 712100, China)

In order to improve the computational accuracy and efficiency of the dynamic reliability analysis of a rotating flexible beam system with additional mass, a monomial cubature rules-based stochastic response surface method (MCR-SRSM) was proposed. A small set of sample pairs for the flexible beam dynamic response was generated by taking the integral points of MCR as sample points. Based on these sample pairs and the regression theory of SRSM, a surrogate model for the implicit feature function for the systematic dynamic response reliability was established. The dynamic response reliability analysis on the flexible beam system was executed by the surrogate model. The simulation results show that the computational precision and efficiency of the proposed method are higher than those of the known traditional Monte Carlo method and Efficient Collocation Method (ECM); under the same coefficients of variation, the dispersion of the cross-sectional width parameter of the flexible beam has a significant effect on the dynamic response reliability.

flexible beam; tip mass; stochastic response surface method (SRSM); monomial cubature rules (MCR); dynamic reliability

TH113.2;TB114.3

A

10.13465/j.cnki.jvs.2017.21.007

中国博士后科学基金(2015M582709)； 中央高校基本科研业务费(2452015058)；中国博士科研启动基金(2452015294)

2016-05-20 修改稿收到日期：2016-07-07

靳红玲 女，博士，讲师，1975年9月

陈军 男，博士，教授，1970年7月