基于同步挤压小波变换的时变结构损伤识别方法研究

刘景良, 任伟新, 黄文金, 黄志伟, 许旭堂

(1.福建农林大学 交通与土木工程学院，福州 350002； 2.合肥工业大学 土木与水利工程学院，合肥 230009)

基于同步挤压小波变换的时变结构损伤识别方法研究

刘景良1, 任伟新2, 黄文金1, 黄志伟1, 许旭堂1

(1.福建农林大学 交通与土木工程学院，福州 350002； 2.合肥工业大学 土木与水利工程学院，合肥 230009)

提出一种基于同步挤压小波变换的时变结构损伤识别方法。采用小波总能量指标识别时变结构的损伤位置，然后对损伤位置处的响应信号进行同步挤压小波变换，识别其瞬时频率并重构本征函数分量信号。在此基础上，求解响应信号的模态振型参与系数比值并联合瞬时频率共同构建了一个新的时变损伤指标(TVDI)。采用一个刚度突变和线性变化的简支梁数值算例对提出的小波总能量和TVDI损伤指标进行了验证，结果表明，提出的指标能够准确地识别结构的损伤位置和时变损伤。

同步挤压小波变换；瞬时频率；模态振型参与系数比值；时变损伤识别；小波总能量

土木工程结构在地震、台风等极端荷载作用下容易产生局部或整体损伤，本质上是时变和非线性结构系统。结构一旦出现损伤，其物理参数必将发生改变，从而导致结构的模态参数发生相应的变化，而识别结构损伤的前提就是如何准确有效地探测出结构损伤过程中物理参数和模态参数的变化[1-2]。小波理论由于其良好的时频局部化特性，近些年来已经广泛运用于结构瞬时特征参数识别。虽然小波变换在时变结构的模态参数识别领域获得了广泛的应用，然而Kijewski等[3]指出，小波变换在分析土木工程结构响应信号中经常出现的长周期信号分量时，往往缺少足够的频率精度。在时频图上表现为低频信号分量的时频曲线分布较宽并且十分模糊。同步挤压小波变换(Synchrosqueezing Wavelet Transform)作为一种以小波变换为基础的全新时频分析方法，通过重组小波变换后的时频图获得了较高频率精度的时频曲线[4-6]。目前，该方法虽有相关的理论研究，然而在实际工程中的应用却还十分缺乏。

时变结构参数识别工作的一个主要应用研究是损伤识别。目前关于时变结构损伤识别方法的研究工作并不多见。Soyoz等[7]采用扩展卡尔曼滤波方法(EKF)识别地震作用下结构的瞬时单元刚度，并以此作为损伤评价指数。熊飞等[8]提出一种基于HHT的时变结构损伤识别方法，该方法采用结构的瞬时频率作为损伤判定指标。任宜春等[9]通过EEMD分解响应信号，提出利用损伤前后结构响应固有模态函数特征能量比和瞬时频率的变化来判断强震作用下结构的损伤位置和损伤时间。在上述时变损伤指标中，瞬时单元刚度难以识别，而瞬时频率指标是一个对全局损伤十分敏感而对局部损伤不敏感的全局量，在实际工程中的应用并不十分理想。Darvishan等[10]采用HHT、Teager能量算子等方法对抗弯框架地震响应进行分析得出：单纯采用频率指标对结构进行损伤识别的精度并不高。

实际上，土木工程结构的损伤是一个由轻微损伤到严重损伤的渐变过程。因此，在有效识别时变结构瞬时特征参数的基础上，如何利用新的数学方法并结合能量、振型等其他参数构造更为实用可靠的时变损伤指标来追踪结构的损伤演化过程，并对结构的健康状况做出准确的评估仍然是一个值得继续深入研究的问题。基于此，本文首先定义小波总能量指标来识别时变结构的损伤位置，然后从损伤位置处的响应信号出发，提出一个类似模态柔度的时变损伤指标来预测结构损伤的演化过程。该指标只需知道瞬时频率和模态振型参与系数比值，并不需要对模态振型进行归一化。新提出的损伤指标的准确性和有效性通过一个刚度突变和线性变化的简支梁数值模型进行了验证。

1 同步挤压小波变换

对于一个时变多分量信号x(t)，一般可以表示为N个本征函数分量信号(IMF)和一个余量之和:

(1)

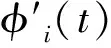
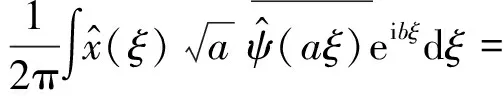
(2)

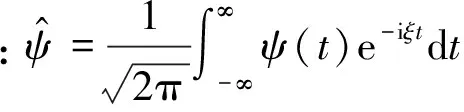
(3)

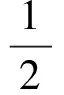
(4)

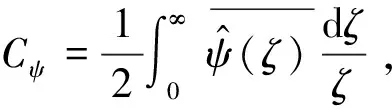
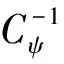
(5)

式中，Re[·]表示求实部。而对应尺度ai的x(b)的分段逼近形式为

(6)

2 小波总能量指标识别损伤位置

结构损伤识别就是将未损结构与损伤结构的动力参数进行比较，从而确定损伤发生的位置、时间和损伤程度，其中首要确定的就是结构的损伤位置。能量是结构振动信号分析中的重要物理量，结构响应信号各组成成分能量的变化包含丰富的结构损伤信息，且临近损伤位置的结构响应信号的能量在损伤前后通常会发生比较大的变化，可以用来表征结构的健康状况和损伤情况。当前基于能量的损伤识别方法主要采用了小波包节点能量这一定义[12-13]。本文采用同步挤压小波变换理论重新定义了小波总能量指标并通过该指标在损伤前后的变化来识别结构的损伤位置。该指标仅需知道结构的响应信号，就能准确识别出结构的损伤位置。

给定任意响应信号x(t)，对响应信号x(t)进行同步挤压小波变换可得系数矩阵Tx(a,b)m×n，其中m代表尺度ai个数，n为采样时间点bj个数。

某个尺度ai下响应信号的小波能量为

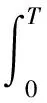
(7)

式中，T为响应信号时间总长。

而小波总能量则定义为各个尺度下的小波能量之和，即

(8)

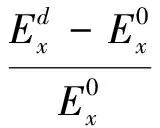
(9)

由于土木工程结构的损伤往往出现某几个位置，当结构某部位发生损伤时，可以看成该部位发生软化，吸收了更多能量，从而导致该位置的小波总能量在损伤前后的变化最大，且为正值，而其他未损部位的ΔEx值相对较小甚至为负值。因此可以通过归一化后的小波总能量变化ΔEx对结构进行损伤定位，然后从损伤位置处的响应信号出发，进一步识别结构的时变损伤。

3 TVDI指标识别时变损伤

由于结构损伤通常会引起结构物理参数的变化，进而导致结构模态参数的变化，因此通过频率和振型等模态参数或者它们的联合指标来识别结构的损伤是十分可行的。作为众多结构损伤识别指标的一种，柔度矩阵是一种十分优越的损伤指标。首先定义柔度增量作为结构系统的损伤指标：

(10)

Δ=F0-Fd

(11)

式中，Φ=[φ1φ2…φi…φN]是质量归一化的模态振型矩阵，下标i表示第i阶模态。ωi表示第i阶模态频率，且Λ=diag(ωi2)。N为结构系统的自由度个数。F0和Fd分别指结构完好无损时和结构损伤时的柔度矩阵。因此Δ反映了结构柔度矩阵的变化，可以用来识别结构的损伤。不同于刚度矩阵，柔度矩阵能够随着模态频率的增加而快速收敛。而模态频率和模态振型也能够轻易地从实验数据和数值响应信号中提取，因此采用模态柔度作为损伤指数是切实可行的。

虽然模态柔度指标已经广泛应用于结构损伤识别研究领域，但是实际上我们很难获得结构柔度的全部信息，尤其是那些含有时变损伤的结构。此外，获得结构的归一化振型也是一件十分困难的事情。受模态柔度损伤指标的启发，我们提出了一个新的时变损伤指标，该指标只需知道结构的瞬时频率和振型参与系数比值，而不需要知道归一化模态振型。由于实际工程中很大一部分信号符合同步挤压小波变换算法的渐进信号假定，因此只要给予足够细的频率划分区间，就能够准确地识别待分析信号中的各个分量信号的瞬时频率。响应信号中的每一个本征函数分量(IMF)也可以通过同步挤压小波逆变换进行完全的重构[14]。在求得结构的瞬时频率和IMF分量的基础上，模态振型参与系数比值(Modal Participation Factor Ratio)可以通过如下方式计算。

设定结构系统中任意两个节点(s和l)的位移响应已知，记为xs(t)和xl(t)。将xs(t)和xl(t)转换到模态坐标，可得

(12)

式中:[φs1φs2φs3…φsN]和[φl1φl2φl3…φlN]分别代表模态振型矩阵的第s行和l行向量，[q1q2…qN]为模态坐标向量，N为结构自由度个数。响应信号中的每一个IMF分量φsiqi或φliqi可以通过同步挤压小波逆变换进行重构。以IMF分量本身作为实部，其Hilbert变换作为虚部，构建解析信号如下：

(13)

式中:H [·]表示Hilbert变换;Aqi表示幅值。以s点作为参考点(通常选择结构响应最大的点)，节点l与s之间的第一阶模态振型参与系数比值φl1,s1定义为

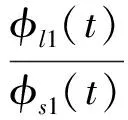
(14)

其他高阶振型参与系数比值可以通过类似方式得到。

在求得结构的瞬时频率和各阶模态振型参与系数比值后，新的时变损伤指标(TVDI)可以定义为

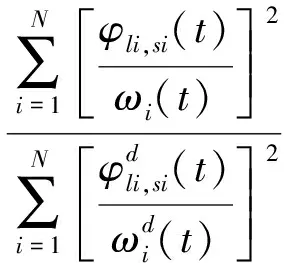
(15)

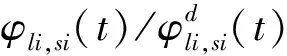
4 瞬时频率提取

由时变损伤指标TVDI的定义可知，瞬时频率的识别精度直接影响TVDI的取值。目前基于小波理论提取小波脊线和瞬时频率的方法主要有两种：一种是基于小波系数的相位信息，一种是基于小波系数的模值信息。然而，无论是基于小波系数相位信息的脊线提取算法，还是基于小波系数模值的脊线提取算法，都面临着一个同样的问题，即提取的小波脊线中存在许多毛刺，从而大大降低了信号瞬时频率的识别精度。而同步挤压小波变换则通过重组小波变换后的时频图提高了瞬时频率的识别精度。

为验证同步挤压小波变换识别信号瞬时频率的准确性，定义如下Duffing非线性系统振动方程：

(16)

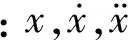
图1 添加5%水平高斯白噪声的Duffing非线性系统位移响应

Fig.1 Displacement responses of Duffing nonlinear system with 5% Gaussian white noise

对含噪Duffing非线性系统位移响应进行同步挤压小波变换和连续小波变换，提取的瞬时频率曲线如图2所示。

图2 同步挤压小波变换和连续小波变换方法识别的Duffing非线性系统响应瞬时频率

Fig.2 Instantaneous frequency of Duffing nonlinear system identified by synchrosqueezing wavelet transform and continuous wavelet transform

从图2可知，由于高斯白噪声的影响，基于连续小波变换(虚线所示)提取的瞬时频率曲线存在许多毛刺，严重影响了瞬时频率的识别精度。而同步挤压小波变换通过细化时频曲线，基本消除了噪声的影响，提高了瞬时频率的识别精度。

5 简支梁损伤识别数值算例

为验证所提出的小波总能量和TVDI指标是否适合具有分布质量的连续系统，本文以简支梁数值算例为研究对象，对刚度突变和线性变化两种情况下结构的损伤进行了识别。简支梁长5 m，划分为20个等长的单元，单元编号和节点编号如图3所示。简支梁密度ρ=7 800 kg/m3，初始弹性模量E0=2.1×105MPa，横截面面积A=0.04 m2(0.2 m×0.2 m)，惯性矩I=1.333×10-4m4。

图3 简支梁模型

5.1单点损伤识别

首先考虑具有单个损伤位置的简支梁的四个损伤工况(Damage Scenario, DS)，如表1所示。土木工程结构的损伤主要表现为刚度的降低，而某个位置刚度的降低可以通过降低该处单元的弹性模量来实现。在损伤工况DS1和损伤工况DS3中，模拟了简支梁的自由振动，其初始位移响应为0.02 m；在损伤工况DS2和损伤工况DS4中，简支梁的外加激励为1940 El Centro地震波。采用Newmark积分法求解简支梁各个节点的位移、速度和加速度响应，时间间隔为0.02 s，整个时间历程为12 s。为考虑噪声的影响，对响应信号添加了5%、10%和15%水平的高斯白噪声作为对比，噪声强度由信噪比(SNR)定义。为简单起见，图4中只表示了损伤工况DS3中简支梁的自由响应。

表1 单点时变损伤四个损伤工况

从图4中可以看出，损伤处节点6和未损处节点11的位移变化趋势基本一致，只是由于节点11位于简支梁跨中，位移幅值相对大一些。

由于简支梁的两个端节点(节点1和21)为铰接，竖向位移响应为零，因此采用复Morlet小波对节点2～20的位移响应进行同步挤压小波变换，并根据式(7)～(9)构建各节点的小波总能量变化ΔEx，如图5所示。由图5可知，节点6(单元5和6中心)处的小波总能量变化ΔEx最大，且为正值，因此该节点应为损伤所在位置，这与表1中的损伤工况描述是十分吻合的。因此，采用小波总能量指标的变化值ΔEx来识别时变结构的损伤位置是十分可行的。

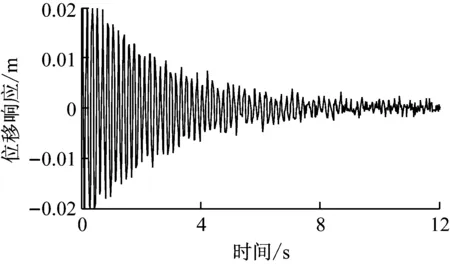
(a) 节点11

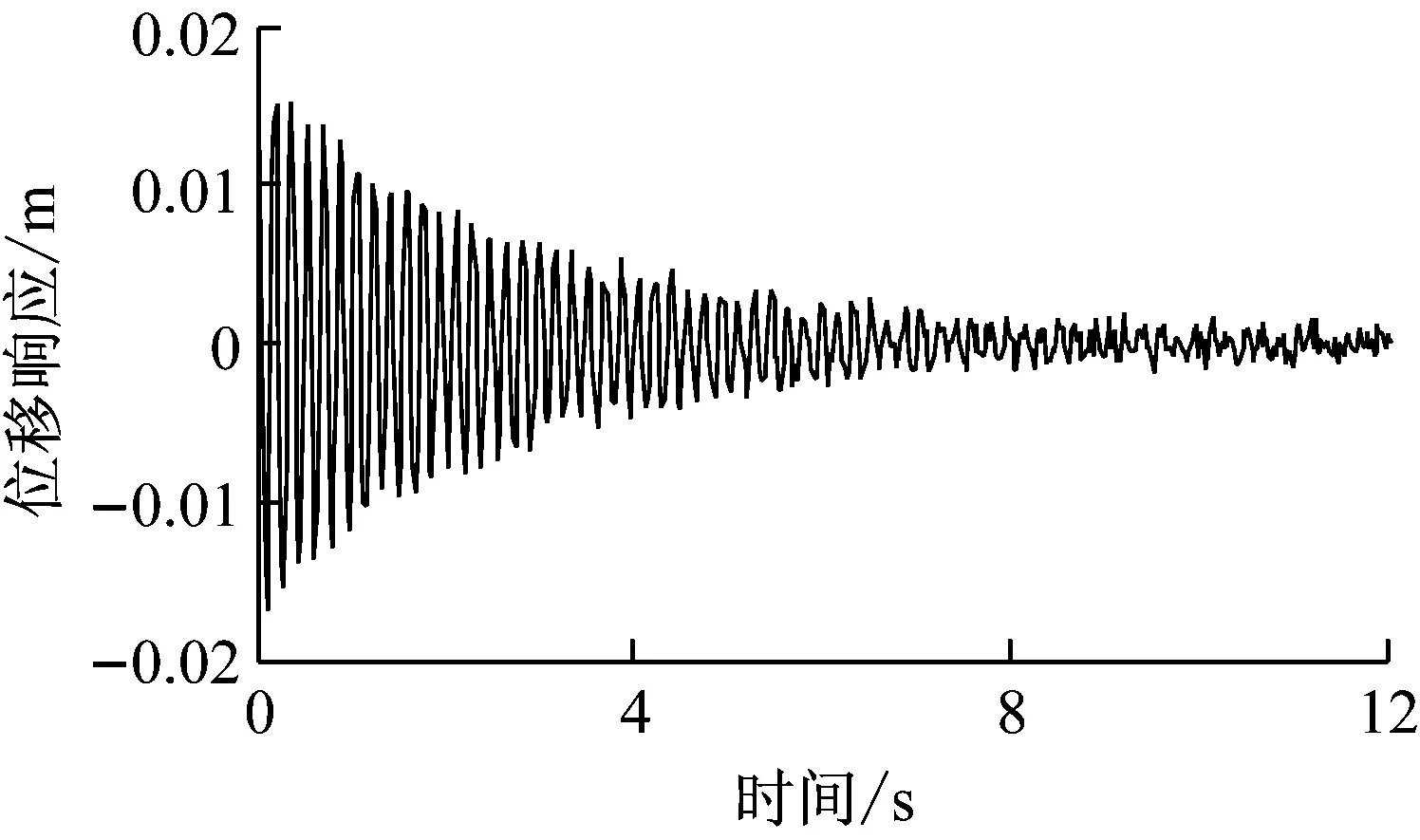
(b) 节点6

(a) DS1

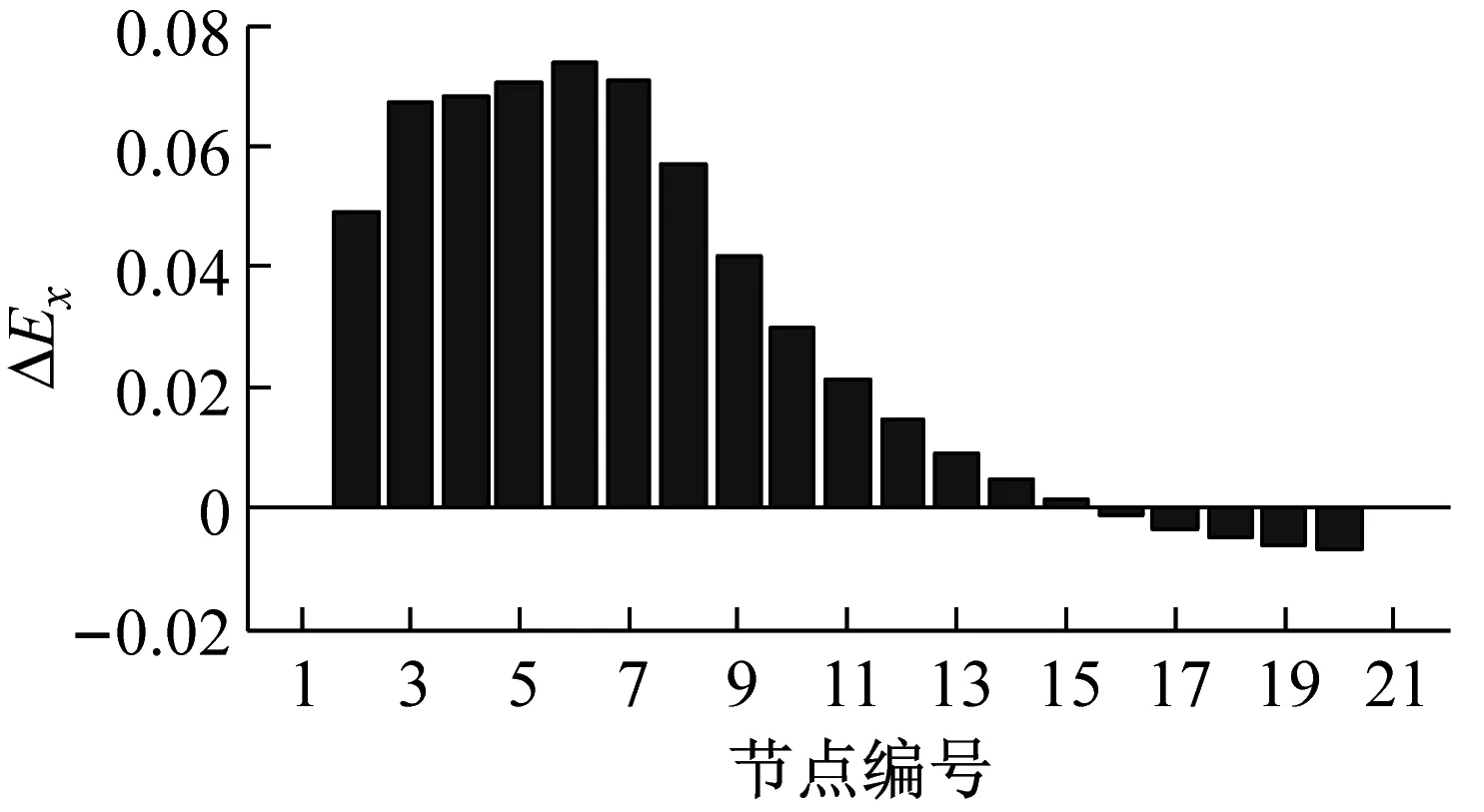
(b) DS2

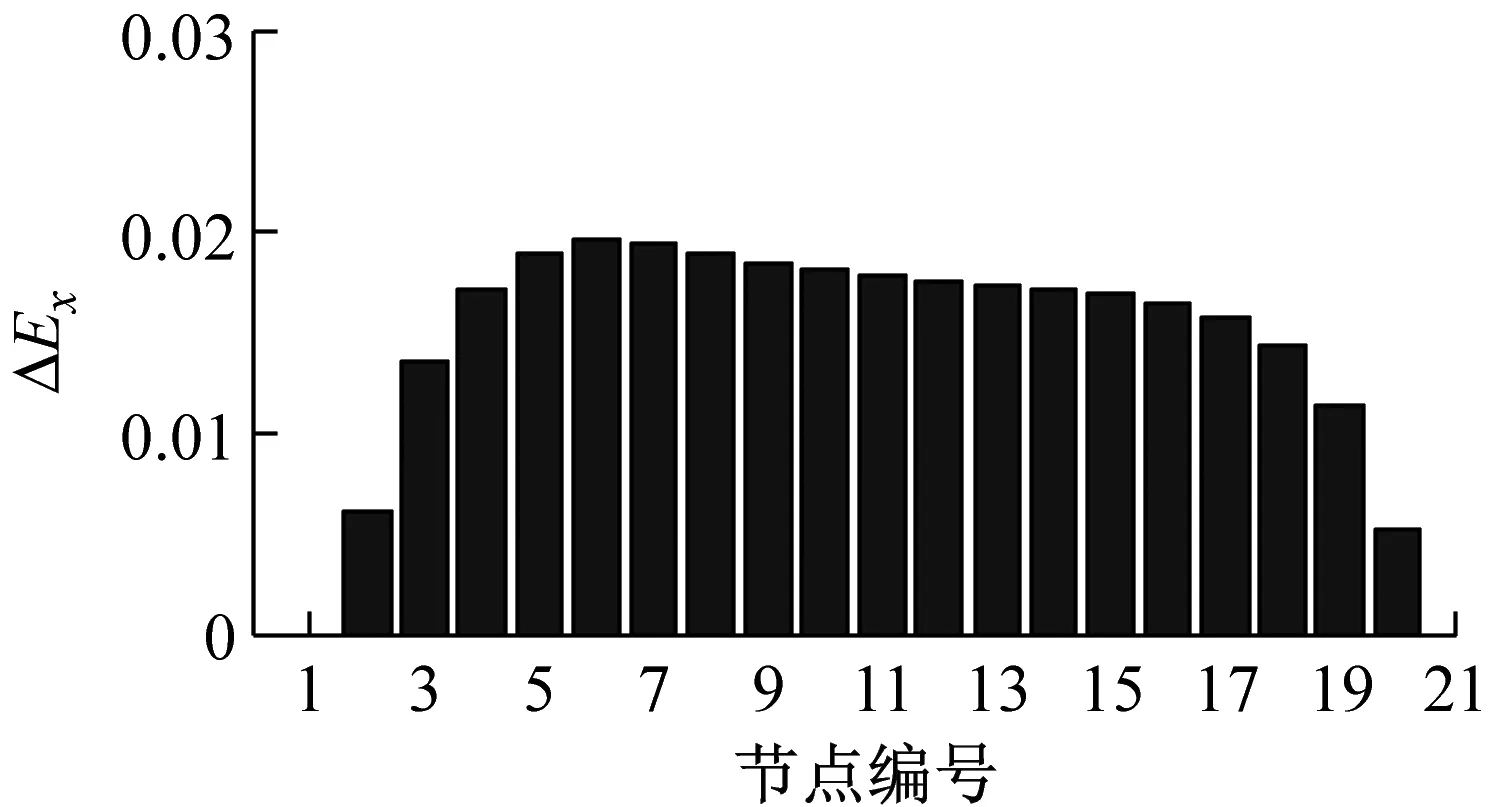
(c) DS3

(d) DS4

图5 四个工况中简支梁的损伤位置识别结果

Fig.5 Damage location identification results for different damage scenarios

已知结构的损伤位置为节点6，为求解时变损伤指标TVDI，首先对简支梁损伤节点6的位移响应进行同步挤压小波变换并提取其瞬时频率，然后将节点11定义为参考点，并根据式(12)～(14)计算损伤状态下的节点6和11间的第一阶模态振型参与系数比值，其中公式中需要用到的IMF分量可以通过对节点6和11的位移响应进行同步挤压小波逆变换重构得到。相应地，完好状态时的瞬时频率和模态振型参与系数比值可以通过同样的方法得到。至此，损伤指标TVDI的值可以通过式(15)计算得到。

四个损伤工况(DS1-DS4)下的时变损伤指标(TVDI)如图6所示。从图6可知，无论是刚度突变还是刚度线性变化，提出的损伤指标TVDI均能够有效地探测到损伤的发生。在图6(a)和图6(b)中，TVDI在t=2 s时的突然增加与简支梁四分之一跨处单元5和6在同一时刻刚度突然降低40%有关。相应地，由于损伤工况DS3和DS4中简支梁四分之一跨处单元5和6的刚度在2 s～6 s之间线性下降40%，图6(c)和图6(d)中的TVDI值在同一时间段线性增加。高斯白噪声对损伤识别结果有一定的影响，但是TVDI指标仍然能够准确识别结构的损伤演化趋势。

从图6可以看出，TVDI在损伤发生之前的时间段(前2 s)并不总是为零。产生这种现象的主要原因是小波变换的端点效应。同步挤压小波变换以小波变换为基础，它虽然能够在一定程度上削弱端点效应带来的不利影响，但是并不能消除端点效应。在响应信号的末端同样可以发现端点效应的存在，例如在图6(a)和图6(c)中，TVDI的值在t=10 s～t=12 s这一时间段时增时减，出现了一定的振荡。对于自由响应，还有另外一个因素导致了TVDI在t=10 s～t=12 s时间的变化。从图4中可知，自由振动下位移响应的幅值随时间逐渐降低至噪声水平甚至接近于零，这必然导致信号末端的低信噪比。因此，识别的瞬时频率和模态振型参与系数比值的精确性和有效性将在一定程度上受到影响，而计算得到的TVDI也将呈现出上述的振荡特性。但是，除了在振动的开始端和结束段，新提出的损伤指标能够有效地反映结构的时变损伤。

在图6(b)中，无论是否添加白噪声，TVDI在大约t=6.8 s～t=8.5 s这一时段均有一个突然的降低。究其原因，主要是瞬时频率本身就是一个关于时间的振荡函数，而小波参数的选择加强了这种振荡趋势。根据同步挤压小波的定义，提取的瞬时频率在某一个时间区间为恒定值，但是当它从一个时间区间进入另外一个时间区间时，其值会有一个突然的变化，这也能够解释图6(c)在5 s～6 s时间段存在的一个突然增加。但是，图6(b)和6(c)TVDI中的两个突然变化相对t=2 s时的突变均比较小，因而基本上不影响简支梁的时变损伤识别结果。

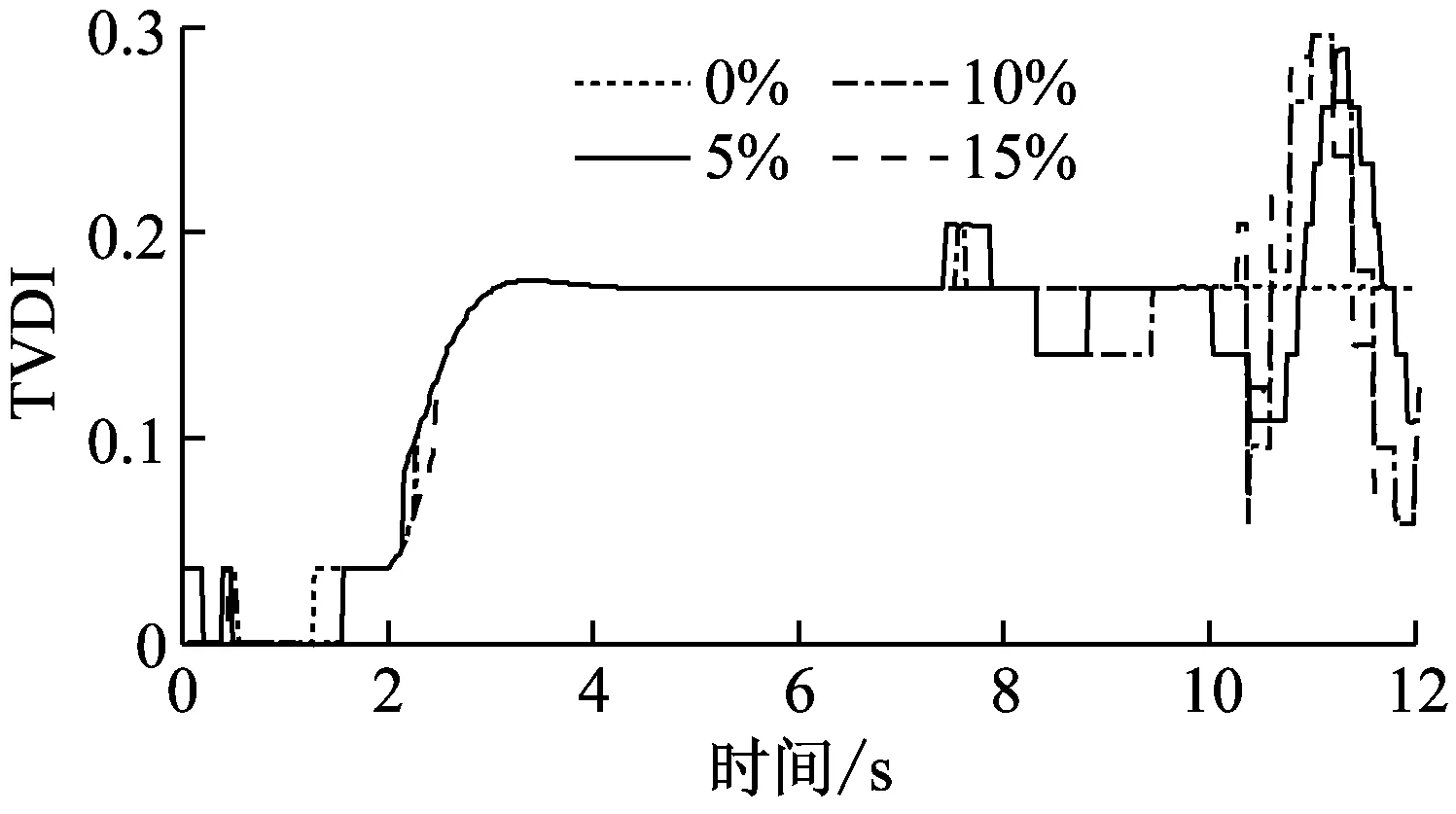
(a) DS1

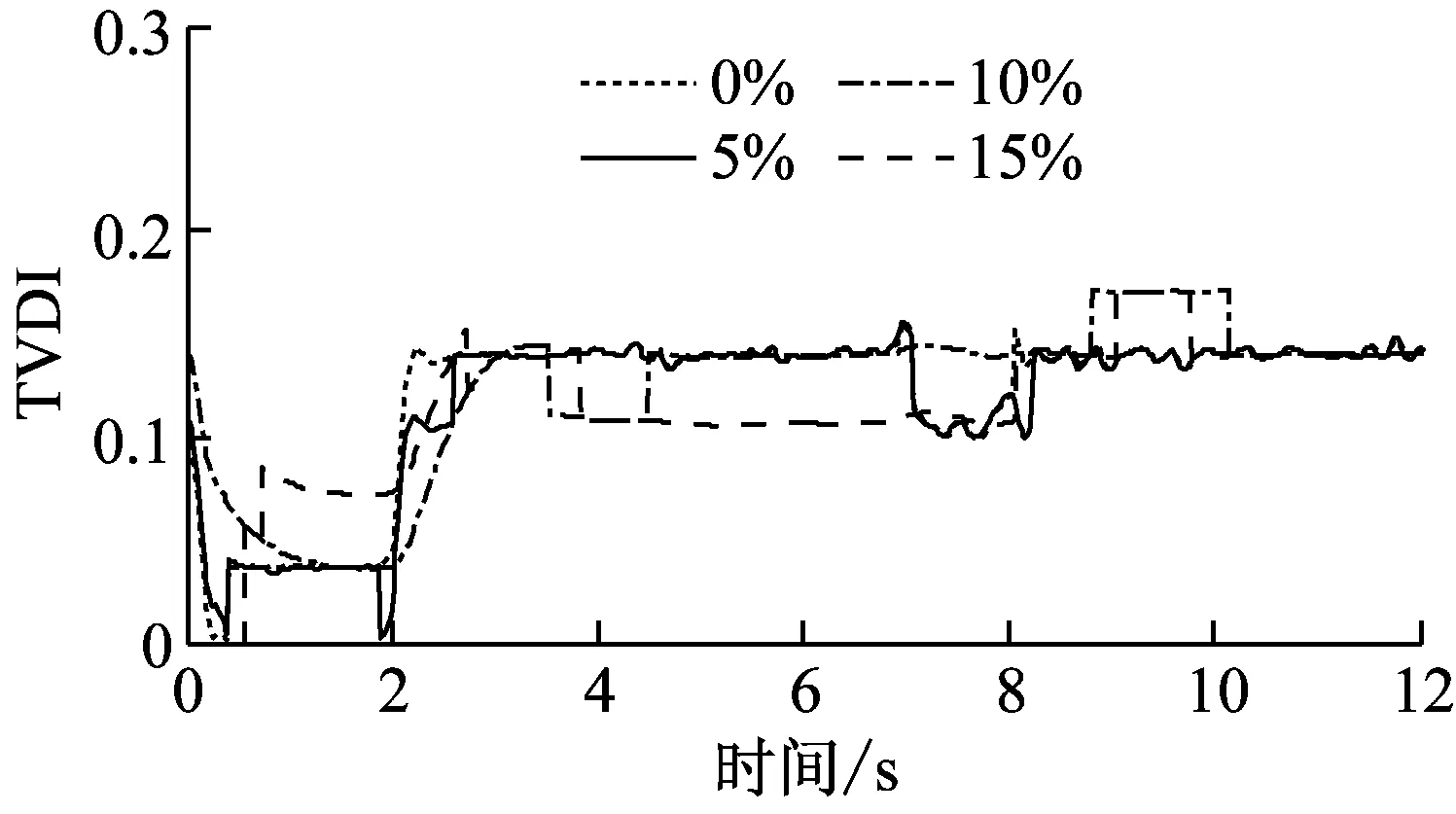
(b) DS2

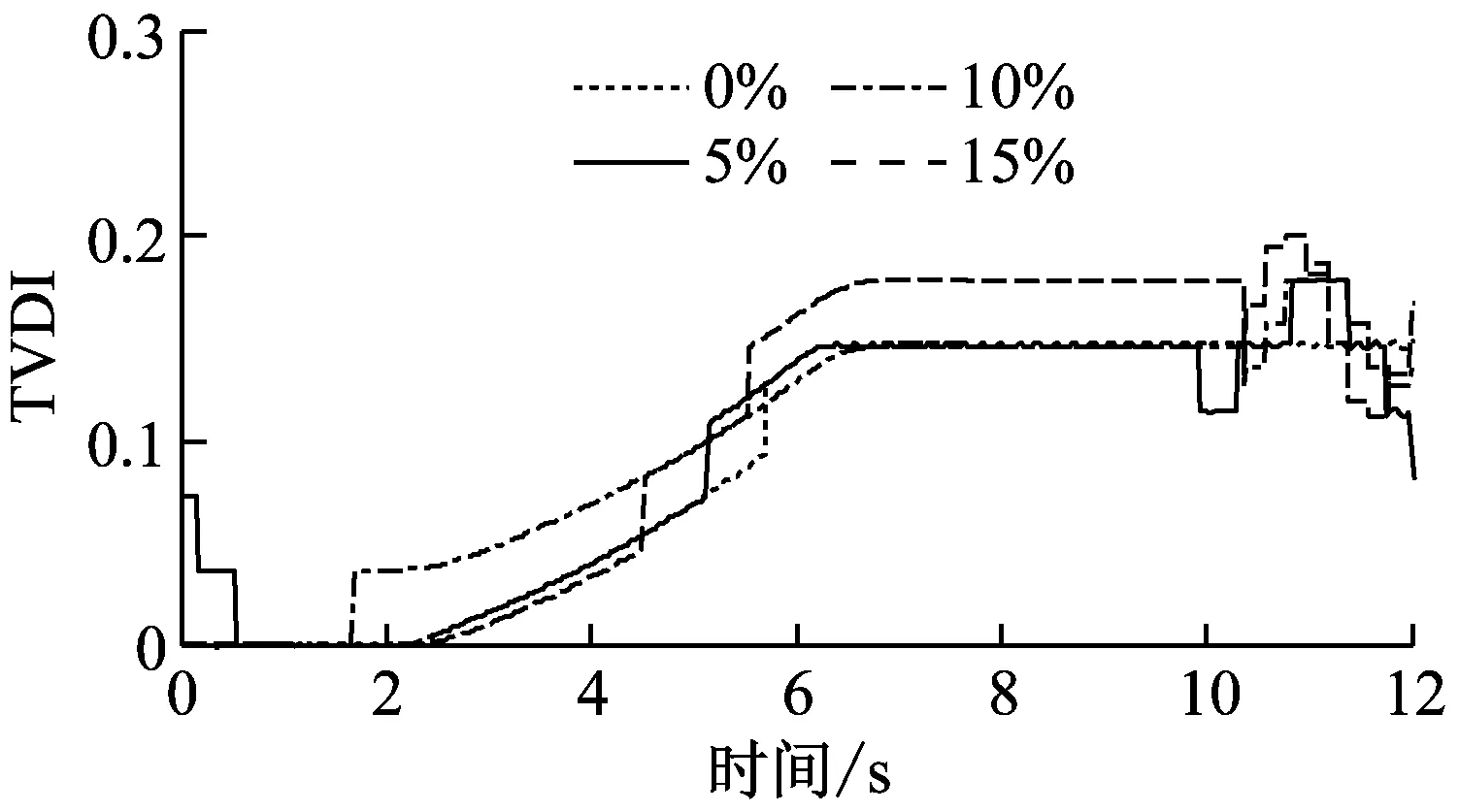
(c) DS3

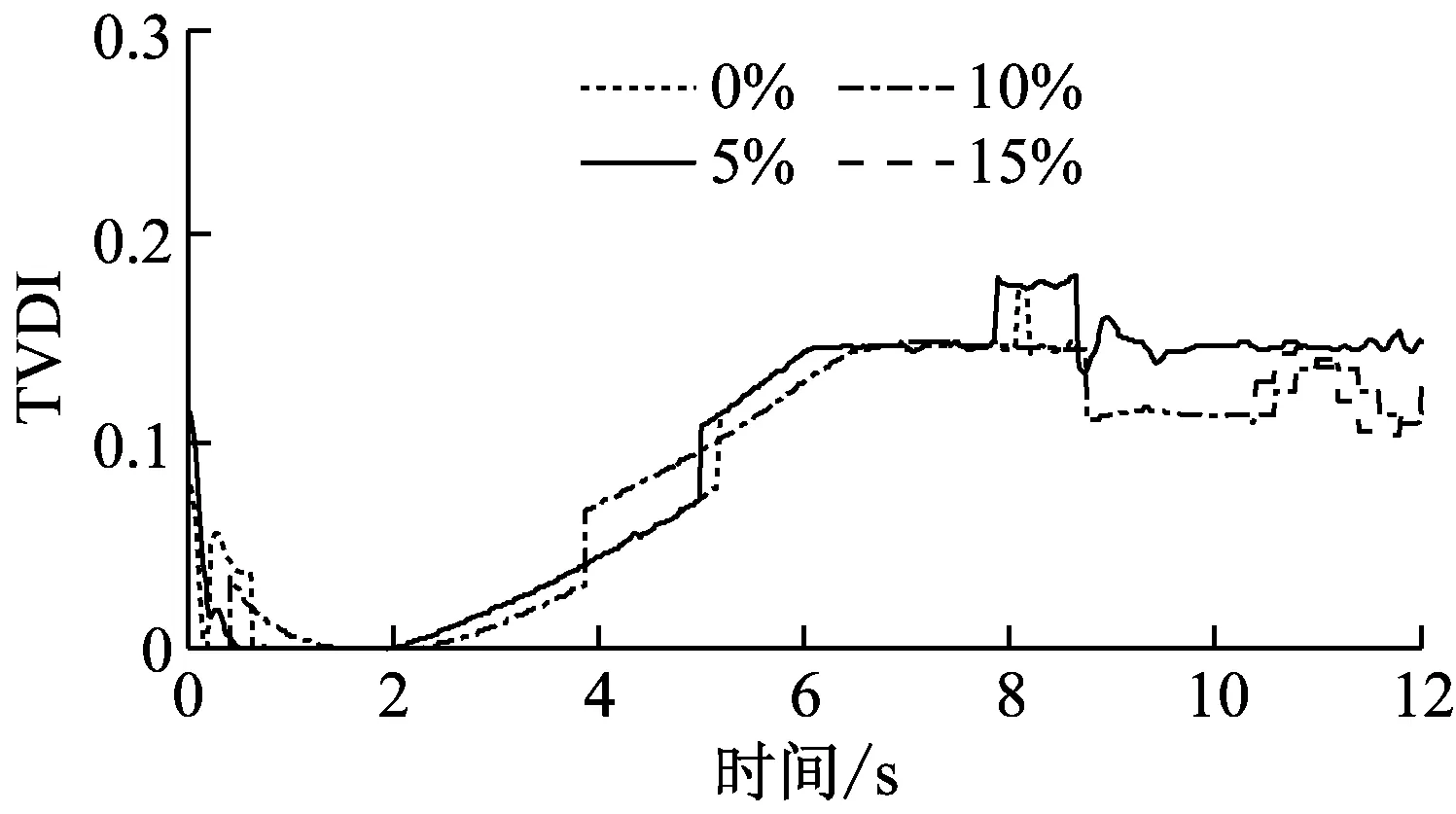
(d) DS4

由于瞬时频率和模态振型参与系数比值的引入， TVDI指标成为一个时变指标，可以用于结构的时变损伤识别，然而小损伤工况下该指标的有效性如何尚未可知。为研究TVDI指标在小损伤工况中的有效性， 仍以上述的简支梁模型为例，考虑了刚度降低10%情况下的四个损伤工况，如表2所示。

表2 四个单点时变小损伤工况

由于已知简支梁结构的损伤位置为节点6，将节点11定义为参考点，对节点6的位移响应进行同步挤压小波变换并提取其瞬时频率，然后根据式(12)～(15)计算相应的第一阶模态振型参与系数比值和损伤指标。四个损伤工况(DS5-DS8)下的时变损伤指标TVDI如图7所示。

从图7可知，无论是刚度突变还是刚度线性变化，提出的损伤指标TVDI均能够有效地识别小损伤工况下结构损伤的发生时间，并且能够准确反映结构的损伤演化趋势。与图6相比，图7中的TVDI值相对较小，这说明提出的时变损伤指标TVDI能够表征结构的损伤程度。当TVDI值较小时，刚度降低幅度较小，结构相对完好。反之，当TVDI取值较大时，结构的损伤程度较大。

5.2多点损伤识别

为了验证提出的TVDI损伤指标能否有效地识别连续分布质量系统多个损伤位置的损伤演化过程，对含有两个损伤位置的上述简支梁进行了损伤识别研究。设定单元5和6的刚度在t=2 s～t=6 s时间段线

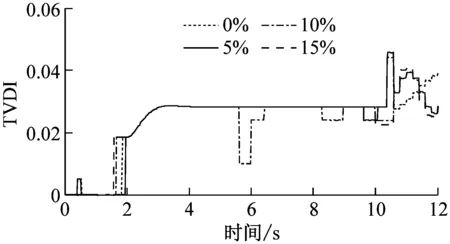
(a) DS5

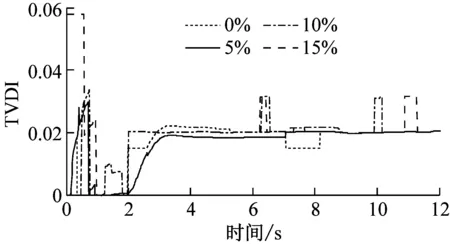
(b) DS6

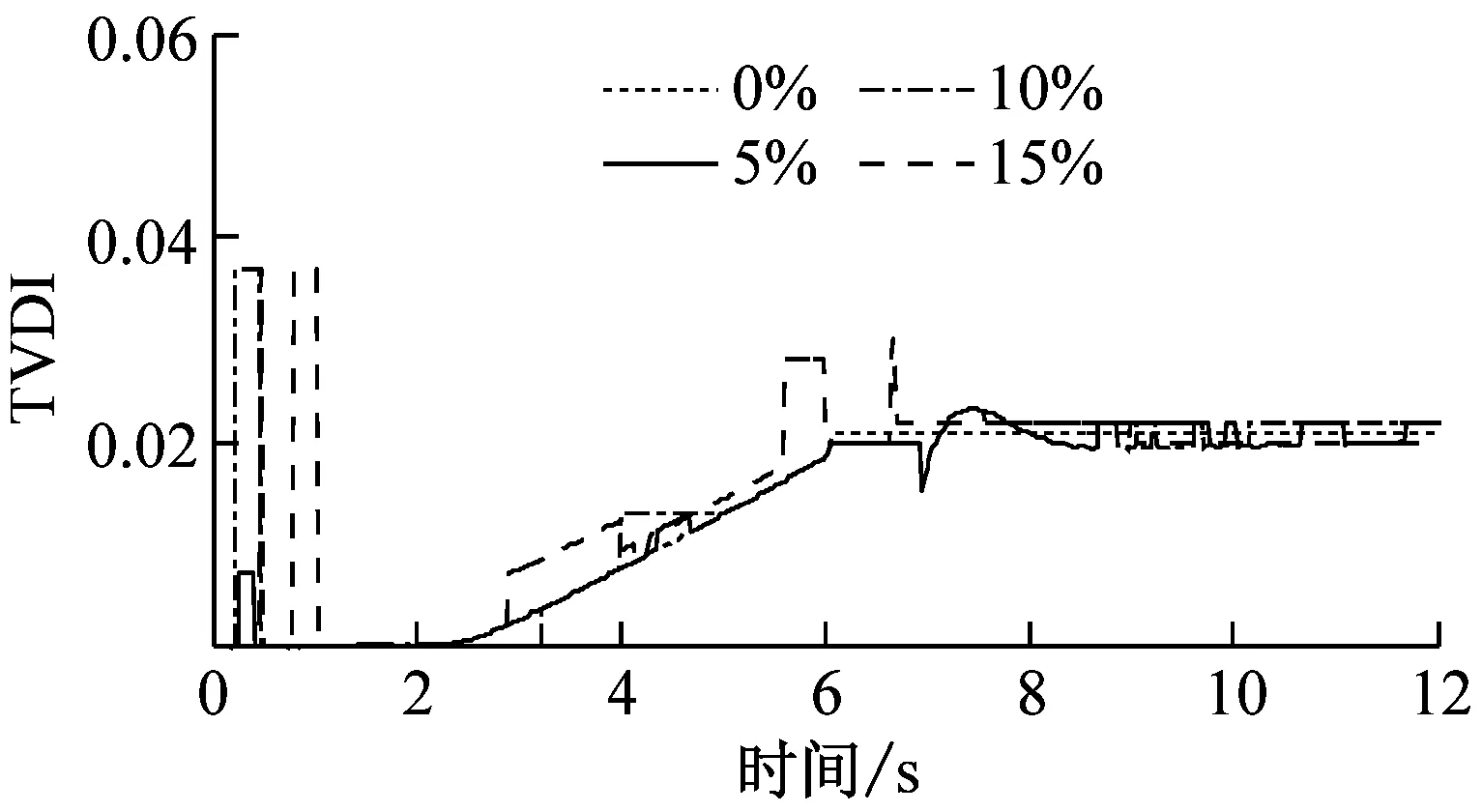
(c) DS7

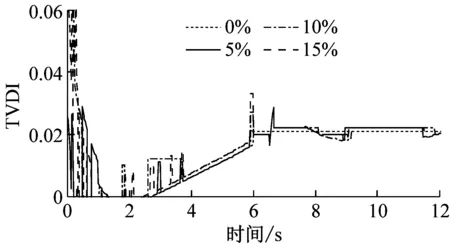
(d) DS8

性降低40%，单元15和16在t=9 s时刚度突然降低40%。采用1940 El Centro地震波作为外加激励，通过Newmark积分求解简支梁结构所有21个节点的位移响应，时间间隔为0.02 s。为考虑噪声的影响，对求得的响应信号添加了5%、10%和15%水平的高斯白噪声作为对比。

采用复Morlet小波对节点2至节点20的位移响应进行同步挤压小波变换，并求解各节点归一化后的小波总能量变化ΔEx，如图8所示。在图8中，节点6和16处的小波总能量变化ΔEx比相邻节点的相应值大，且为正值，因此这两两个节点应为损伤点，这与简支梁的实际损伤情况是十分吻合的。因此，小波总能量指标能够准确识别多点时变损伤结构的损伤位置。

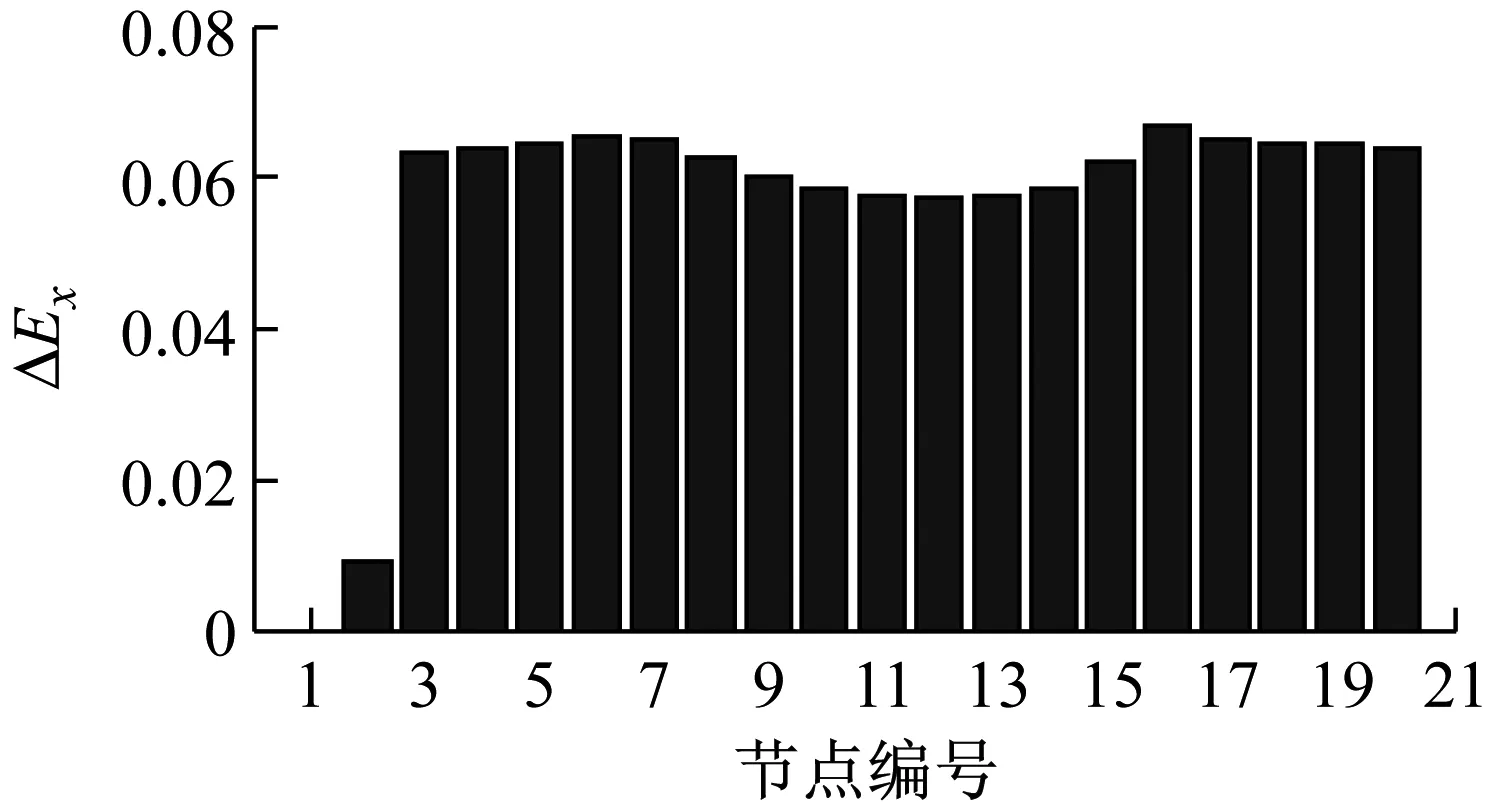
图8 多点损伤的简支梁损伤位置识别结果

Fig.8 Damage location identification results of simple supported beam with two damage locations

对损伤节点6和16的位移响应进行同步挤压小波变换可以有效提取其瞬时频率。与单点时变损伤类似，将跨中节点11设置称为参考点，从节点6和11的位移响应中重构的IMF分量可以用来计算节点6和11间的第一阶模态振型参与系数比值。同理，采用从节点16和11的位移响应中重构的IMF分量来计算节点16和11间的第一阶模态振型参与系数比值。而完好状态下瞬时频率和模态振型参与系数的提取过程与损伤工况下的提取过程类似。至此，可以根据式(15)分别求解节点6和节点16处的时变损伤指标TVDI，其变化情况如图9所示。TVDI的变化表征了结构刚度的变化情况。从图9中可知，单元5和6的刚度在t=2 s～t=6 s时间段的线性变化和单元15和16的刚度在t=9 s时的突然降低基本上都在图9(a)和9(b)中分别得到了如实的反映。TVDI在损伤发生之前的时间段(前2 s)并不总是为零的现象同样存在于图9(a)和9(b)中，其主要原因是同步挤压小波变换的端点效应。高斯白噪声虽然对TVDI的取值造成了一定的干扰，但是TVDI仍然能够准确反映时变结构刚度变化的趋势。因此，采用新提出的时变损伤指标TVDI来追踪含有两个乃至多个损伤位置的简支梁的损伤演化过程是完全可行的。

(a) 节点6

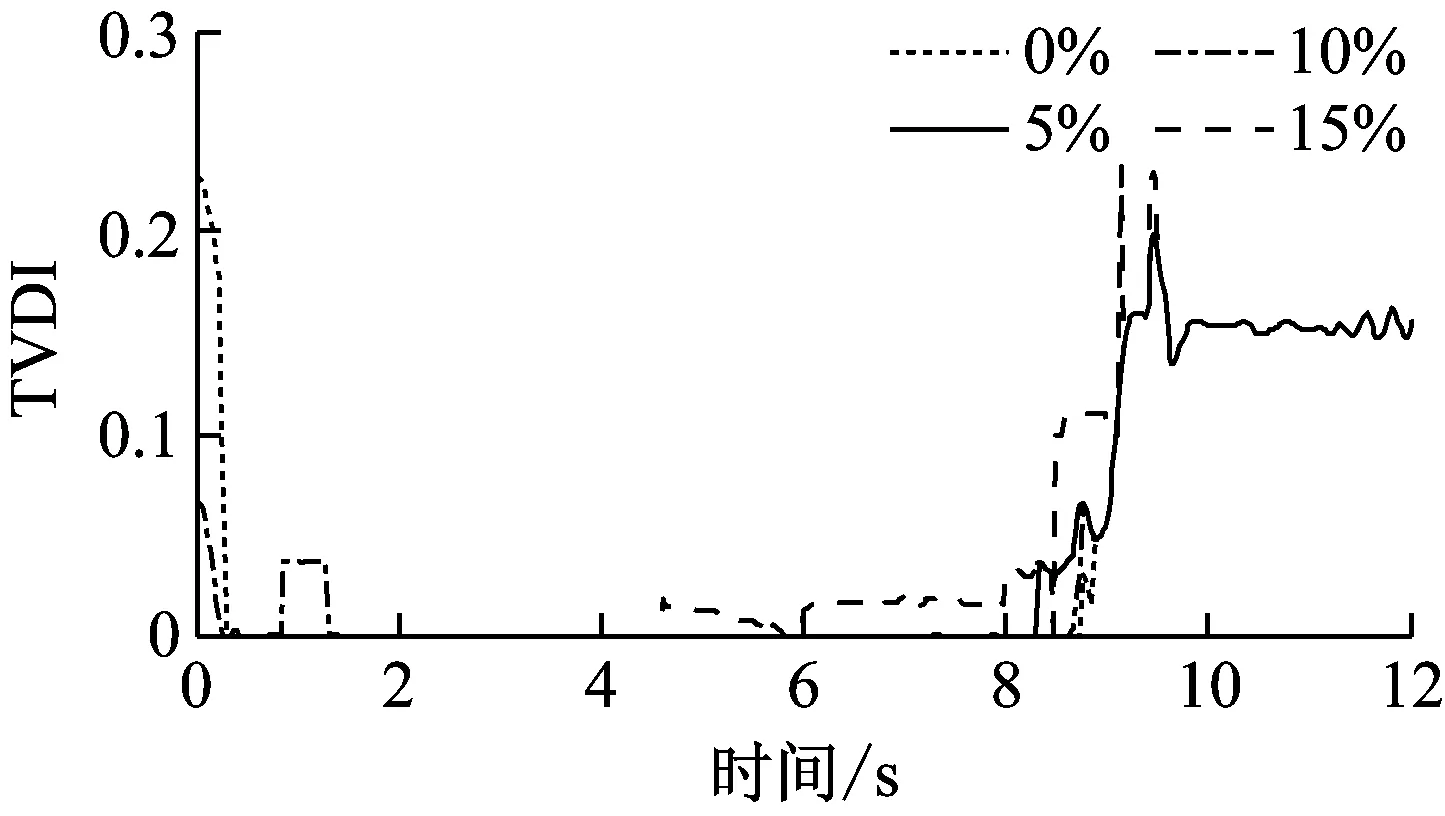
(b) 节点16

Fig.9 Damage identification results of the simply supported beam with two damage locations

与单点损伤识别类似，对多点小损伤工况下TVDI指标的有效性进行研究。设定上述简支梁上的两个位置出现小损伤，即单元5和6的刚度在t=2 s～t=6 s时间段线性降低10%，单元15和16在t=9 s时刚度突然降低10%。外加激励为1940 El Centro地震波，采用Newmark积分求解简支梁节点位移响应，时间间隔为0.02 s。为考虑噪声的影响，对求得的节点位移响应信号添加5%、10%、15%水平的高斯白噪声作为对比。

根据式(12)～(15)求得的TVDI损伤指标如图10所示。由图10可知，即使是在小损伤情况下，新提出的TVDI指标仍然能够准确反映时变结构刚度突变或线性变化的趋势。因此，采用时变损伤指标TVDI追踪两个或多个位置出现小损伤的简支梁的损伤演化过程是可行的。

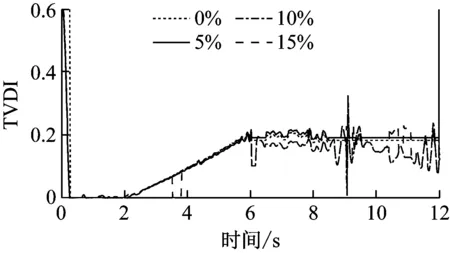
(a) 节点6

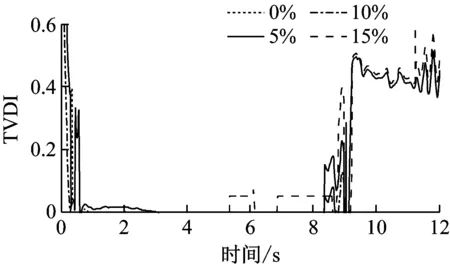
(b) 节点16

Fig.10 Damage identification results of the simply supported beam with two minute damage locations

6 结 论

土木工程结构本质上是时变和非线性结构系统，其损伤是一个由轻微损伤到严重损伤的渐变过程。本文在同步挤压小波变换的基础上，提出归一化的小波总能量和TVDI指标对时变结构的损伤进行识别研究，并通过一个简支梁损伤识别数值算例进行了验证。研究结果表明：

(1) 归一化后的小波总能量指标的变化值能够准确识别单点和多点时变损伤简支梁结构的损伤位置。

(2) 新提出的TVDI指标能够有效识别刚度突变和线性变化时单点损伤简支梁结构的时变损伤，并追踪其损伤演化趋势。

(3) TVDI不但能够准确地识别简支梁结构的单点时变损伤，而且能够有效识别地震作用下简支梁的多点时变损伤。

[1] KOPSAFTOPOULOS F P, FASSOIS S D. A functional model based statistical time series method for vibration based damage detection, localization, and magnitude estimation[J]. Mechanical Systems and Signal Processing, 2013, 39: 143-161.

[2] 闫桂荣，段忠东，欧进萍. 基于结构振动信息的损伤识别研究综述[J]. 地震工程与工程振动，2007，27(3)：95-102.

YAN Guirong, DUAN Zhongdong, OU Jinping. Review on structural damage detection based on vibration data[J]. Journal of Earthquake Engineering and Engineering Vibration，2007, 27(3): 95-102.

[3] KIJEWSKI K, KAREEM A. Wavelet transforms for system identification in civil engineering [J]. Computer-Aided Civil and Infrastructure Engineering, 2003, 18: 339-355.

[4] DAUBECHIES I, LU J, WU H T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool[J]. Applied and Computational Harmonic Analysis, 2011, 30(2): 243-261.

[6] 刘景良，任伟新，王佐才，等. 基于同步挤压小波变换的结构瞬时频率识别[J]. 振动与冲击，2013，32(18)：37-42.

LIU Jingliang, REN Weixin, WANG Zuocai, et al. Instantaneous frequency identification based on synchrosqueezing wavelet transformation[J]. Journal of Vibration and Shock, 2013, 32(18): 37-42.

[7] SOYOZ S, FENG M Q. Instantaneous damage detection of bridge structures and experimental verification[J]. Structural Control and Heath Monitoring, 2008, 15: 958-973.

[8] 熊飞，程远胜，刘均. 基于HHT方法的时变多自由度系统的损伤识别[J]. 振动、测试与诊断，2008，28(2)：122-125.

XIONG Fei，CHENG Yuansheng，LIU Jun. Damage identification of time varying multi-degrees of freedom systems based on Hilbert-Huang transform[J]. Journal of Vibration, Measurement & Diagnosis, 2008, 28(2): 122-125.

[9] 任宜春，翁璞. 基于改进Hilbert-Huang变换的结构损伤识别方法研究[J]. 振动与冲击，2015，34(18)：195-199.

REN Yichun，WENG Pu. Structural damage detection based on improved Hilbert-Huang transform[J]. Journal of Vibration and Shock, 2015, 34(18): 195-199.

[10] DARVISHAN E, AMIRI G G, GHADERI P. A study on instantaneous time-frequency methods for damage detection of nonlinear moment-resisting frames[J]. Shock and Vibration, 2014(1): 1-14.

[11] 刘景良，任伟新，王佐才. 基于同步挤压和时间窗的时变结构损伤识别[J].振动工程学报，2014，27(6)：835-841.

LIU Jingliang, REN Weixin, WANG Zuocai. Time-varying structural damage detection based on synchrosqueezing and time window method [J]. Journal of Vibration Engineering, 2014, 27(6)：835-841.

[12] YEN G G, LIN K C. Wavelet packet feature extraction for vibration monitoring [J]. IEEE Transactions on Industrial Electronics, 2000, 47(3): 650-667.

[13] 韩建刚，任伟新，孙增寿. 基于小波包变换的梁体损伤识别[J]. 振动、测试与诊断，2006, 26(1): 5-10.

HAN Jiangang, REN Weixin, SUN Zengshou. Damage detection of beams based on wavelet packet analysis[J]. Journal of Vibration, Measurement & Diagnosis, 2006, 26(1): 5-10.

[14] WANG Z C, REN W X, LIU J L. A Synchrosqueezed Wavelet transform enhanced by extended analytical mode decomposition method for dynamic signal reconstruction[J]. Journal of Sound and Vibration, 2013, 332(22): 6016-6028.

Damagedetectionfortime-varyingstruturesbasedonthesynchrosqueezingwavelettransform

LIUJingliang1,RENWeixin2,HUANGWenjin1,HUANGZhiwei1,XUXutang1

(1. School of Transportation and Civil Engineering, Fujian Agriculture and Forestry University, Fuzhou 350002, China； 2. School of Civil and Hydraulic Engineering, Hefei University of Technology, Hefei 230009, China)

A new damage detection method for time-varying structures based on the synchrosqueezing wavelet transform was proposed. The wavelet total energy index was employed to detect damage locations, and then the synchrosqueezing wavelet transform was performed on the response signals at the structural damage locations. As a result, the instantaneous frequencies were extracted and individual component signals were reconstructed. A new time-varying damage index(TVDI) was defined based on the extracted instantaneous frequencies and modal participation factor ratio calculated from the reconstructed individual components. A simply supported beam structure with abrupt and linear time-varying damage was simulated numerically to verify the effectiveness of the presented method. The results demonstrate that the defined time-varying damage index can effectively detect damage locations and track structural time-varying damages.

synchrosqueezing wavelet transform; instantaneous frequency; modal participation factor ratio; time-varying damage detection; wavelet total energy

TN911.6；TU311.3

A

10.13465/j.cnki.jvs.2017.21.002

国家自然科学基金青年项目(51608122)；福建省青年科技人才创新项目(2016J05111)

2016-10-09 修改稿收到日期：2016-12-29

刘景良，男，博士，讲师，1983年生