基于IRP和TD2DPCA的轴承故障诊断方法

岳应娟， 孙 刚， 蔡艳平， 王新军

(1.火箭军工程大学 理学院，西安 710025；2.火箭军工程大学 五系，西安 710025)

基于IRP和TD2DPCA的轴承故障诊断方法

岳应娟1， 孙 刚1， 蔡艳平2， 王新军2

(1.火箭军工程大学 理学院，西安 710025；2.火箭军工程大学 五系，西安 710025)

针对轴承振动信号的非平稳特征和现实中难以提取故障参数的情况，提出了一种基于图像的轴承故障诊断方法即基于递归灰度图(Improved Recurrence Plots，IRP)和双向二维主成分分析(Two directional, Two dimensional Principal Component Analysis,TD2DPCA)的轴承故障诊断法。该方法对递归图(Recurrence Plots，RP)中阈值选取的问题进行了优化，提出了IRP算法，对采集到的轴承振动信号进行IRP分析，生成递归灰度图；然后用TD2DPCA对生成的递归灰度图进行特征参数提取，得到系数编码矩阵；最后采用分类器对上述编码矩阵直接进行模式识别，以实现轴承故障的自动化诊断。将该方法应用在轴承4种典型工况的故障诊断实例中，识别率高达99.8%，结果表明：基于IRP和TD2DPCA的轴承故障诊断方法能够自适应的对轴承进行故障诊断，具有故障识别精度高、噪声鲁棒性好等优点，为轴承振动诊断探索了一条新途径。

轴承;递归图;递归灰度图;双向二维主成分分析;故障诊断

滚动轴承在旋转机械中具有广泛的应用,其运行状态对整个机械系统的精度、可靠性及寿命具有很大影响，因此对轴承的状态监测与故障诊断具有重要意义。当轴承的某一元件表面出现局部损伤时，在负载运行过程中其他元件表面与之相互作用，产生周期性的冲击，因此若轴承出现故障，其故障信息必然会直接在振动信号中反映出来，并且由于轴承振动分析诊断方法的不解体性和实时性，因此一直是轴承故障诊断的前沿和研究热点。

国内外学者围绕轴承振动分析诊断方法做了大量研究,唐贵基等[1]提出一种基于变分模态分解和包络解调运算的轴承故障诊断方法；丁建明等[2]提出一种基于经验模态分解和谱峭度的改进包络谱滚动轴承故障诊断方法；李学军等[3]将小波包与近似熵相结合用于圆柱滚子轴承诊断；程发斌等[4]将谐波小波包变换与信息熵相结合并成功用于轴承3种工况的诊断中。这些方法为轴承故障诊断提供了必要的手段，但是包络分析方法在形成包络信号时需要依靠经验来确定所感兴趣的解调频带参数,这在主观上会给分析结果带来很大影响[5]；利用近似熵和能量熵在进行诊断时，信号分解方法中参数的设定与近似熵和能量熵的值有着直接关系，并直接影响诊断结果。

本文在总结前人工作的基础上，另辟蹊径提出一种基于图像的IRP和TD2DPCA故障诊断新方法，避免了传统方法中人为因素对识别准确率的影响，具有较好的自适应性和噪声鲁棒性。使用该方法直接对采集到的含噪轴承振动信号进行递归灰度图分析，自适应特征参数提取，分类器智能识别，结果表明，该方法具有较高识别精度，适用于滚动轴承的故障诊断。

1 递归图

1.1递归图

递归图是由Eckmann等[6]在1987年提出的, 用来表示确定性动力学系统、非线性系统和混沌系统的基本特性的一种方法。其构造算法如下[7]：

1) 假设给定的离散时间序列{xi,i=1,2,…,L}，以延时常数τ，嵌入维数m来进行伪相空间重构：

Yi={xi,xi+τ,…,xi+(m-1)τ}

i=1,2,…,L-(m-1)τ

(1)

2) 计算伪相空间轨迹上的第j点Yj与第i点Yi之间的距离：

(2)

3) 构造一个N×N点的方图，图中横坐标与纵坐标代表伪相轨道上点的序号如图1如示。规定：

其中r为邻域半径，为一事先设定值。

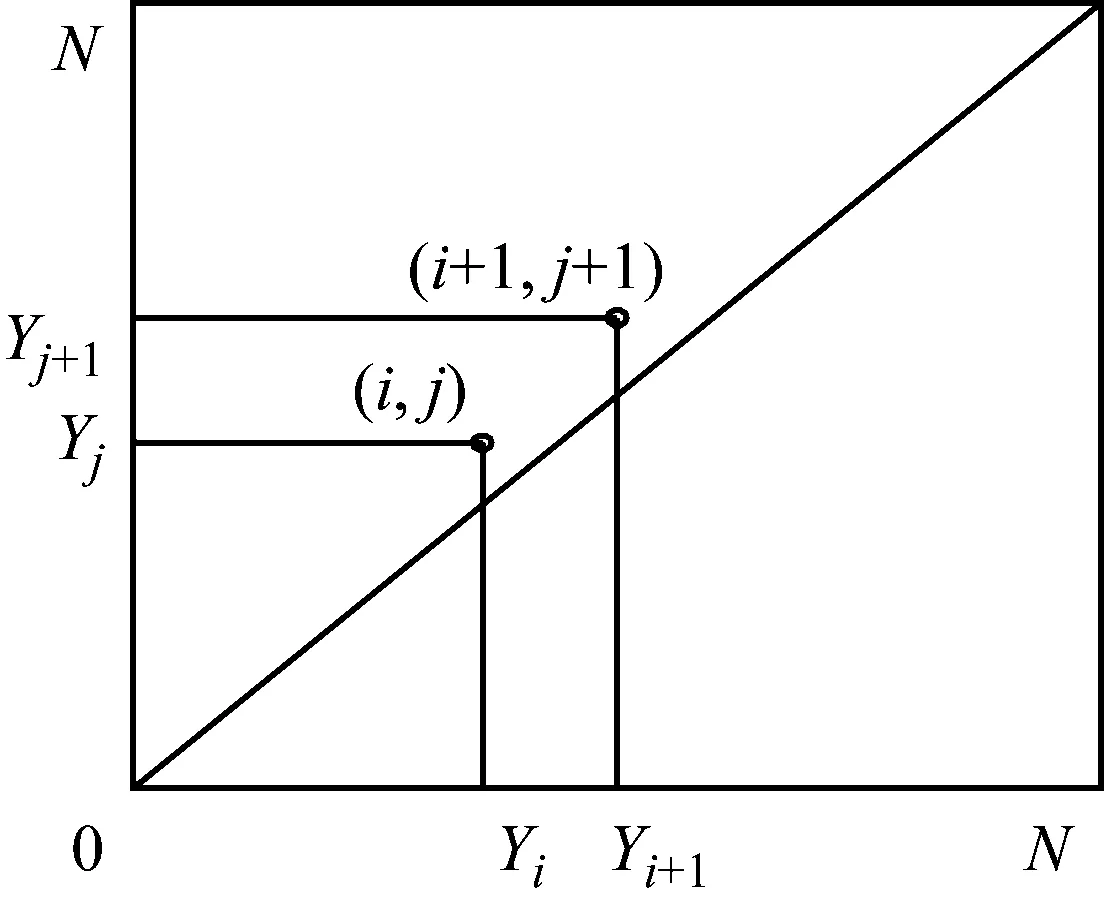
图1 递归图构造示意图

1.2递归灰度图

从构造原理可得出，递归图中的细节纹理体现了对应系统包含的时间相关信息，而同时整幅图又展现了系统的全局拓扑性质。因此，递归图可以被用来描述系统的平稳度。当系统的行为是完全平稳时，那么它的递归图就应是一张均匀分布的图形，而当系统处于非稳态结构时，时间相关信息在递归图上就会表现出细微的纹理结构，随着不平稳性的增加，其在递归图上表现出的纹理结构也会更加突出[8-9]。

从递归图的构造过程可知，递归图描述的是系统稳态运行时的状态，是对系统状态复杂程度的一个定性描述。对于轴承故障诊断和状态监测而言，必须提取反映系统状态的定量诊断或监测指标。分析递归图构造算法可知：在作图时只是简单地将距离进行分离，即小于阈值r这样的点对之间的信息得到了保留，而且即使是这样，对凡是距离小于r的点对一视同仁，即不加区分，只是笼统地将它们归为一类，点对距离小于r的程度无法反映；而距离大于r的点对之间的信息也完全丢弃了，重构后距离大于r的点对在整个相空间中的所占比例及距离大于r的程度等重要信息无法得到反映，而这显然不利于对系统状态进行准确的判断和识别。

本文在对递归图构造算法研究的基础上，提出一种能更全面反映系统复杂程度的定性指标：递归灰度图。其构造算法如下：

① 重构相空间(式(1))。

② 计算点对之间的距离(式(2))。

③ 构造一个N×N点的方图，如图1如示。

④ 令：

dmax=max{dist(i,j;m)}

i,j=1,2,…,N-(m-1)τ

(3)

又令：dist(i,j;m)=255×dist(i,j;m)/dmax

(4)

对dist(i,j;m)取整，并在相应的N×N点的方图上作出相应灰度值的点，这样构成的灰度图称之为“递归灰度图”。

分析递归灰度图的算法可知：对点对之间的距离进行灰度归一化处理(255级，式(4))，而不是简单地对距离的大小进行分离处理，距离小于r的点对之间的信息得到了利用，而距离大于r的点对所反映的系统信息也得到了利用，并且不同灰度级在图象中所占比例的大小还可以反映距离分布情况，因而递归灰度图是系统状态在重构相空间上更全面的反映，更有利于故障诊断与状态识别。

仿真信号采用多频信号X(t)和标准差为1的随机噪声信号叠加所得，用以模拟轴承的周期性冲击：

X(t)=[1+cos(2π×30t)]×cos(2π×125t)+

[1+cos(2π×30t)]×cos[2π×155t+cos(2π×5t)]+

[1+cos(2π×30t)]×cos(2π×185t)

(5)

图2和图3所示，为白噪声和仿真信号的递归灰度图和不同阈值条件下的递归图，根据Takens空间嵌入理论[10]和本文信号特点取递归图(或递归灰度图)中的嵌入维数m=3，延时常数则采用平均位移法[11]求得τ=1。

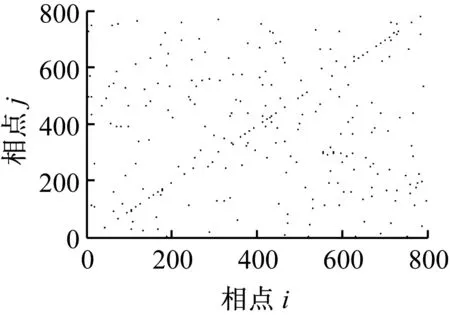
(a) r=0.2×distmax

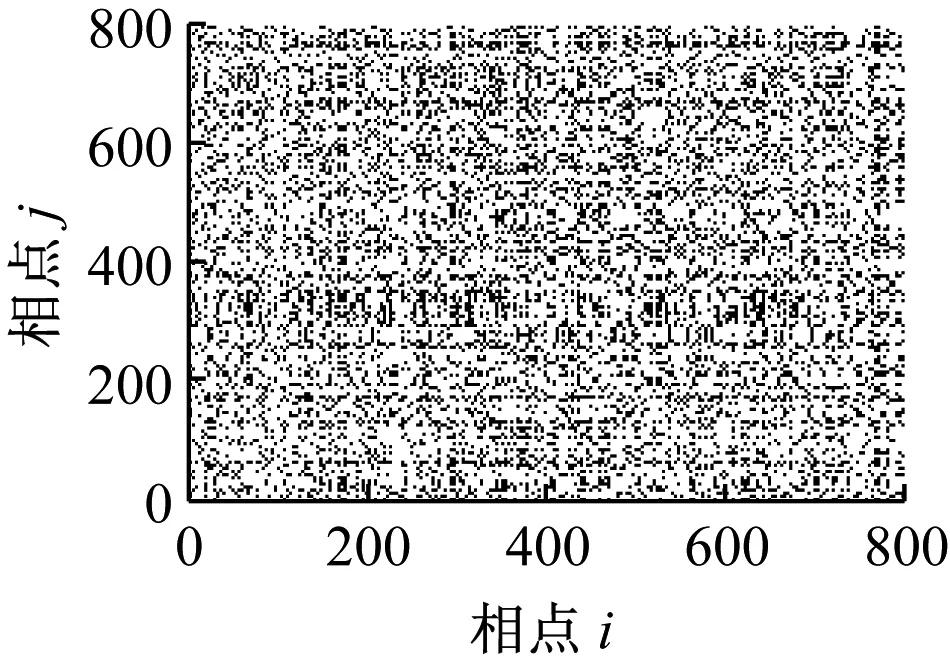
(b) r=0.3×distmax

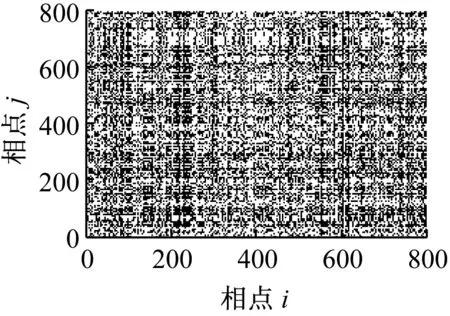
(c) r=0.5×distmax

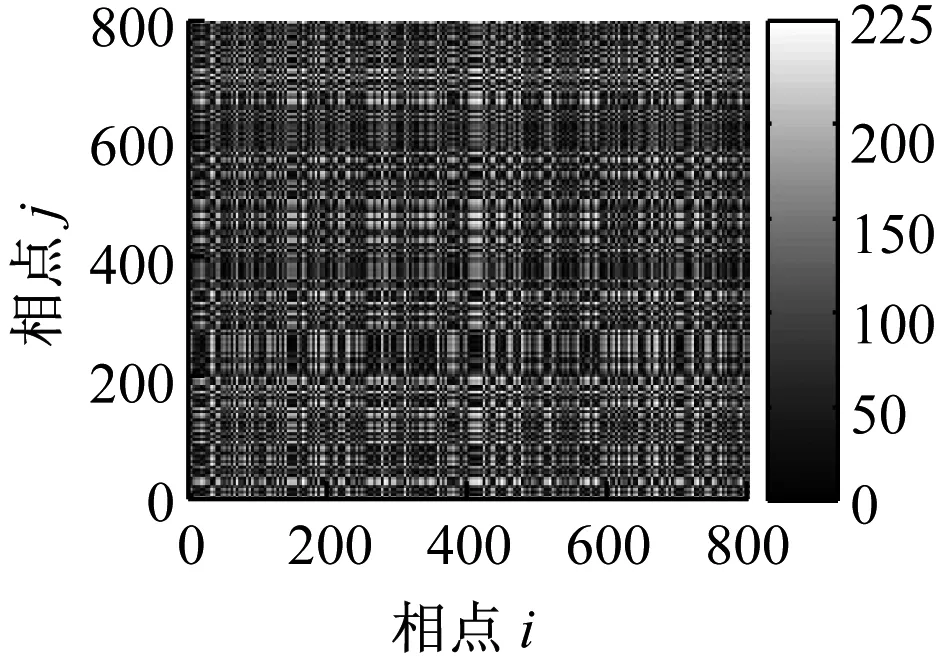
(d) 递归灰度图

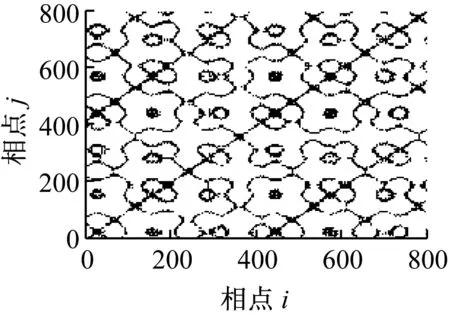
(a) r=0.2×distmax

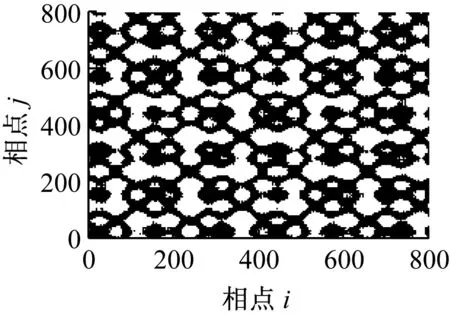
(b) r=0.5×distmax

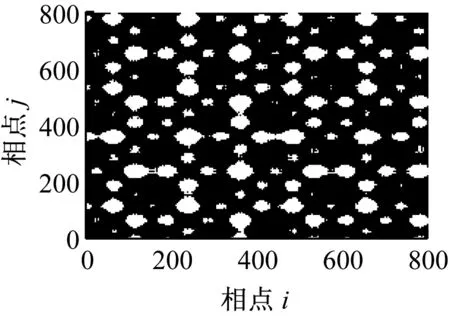
(c) r=0.8×distmax

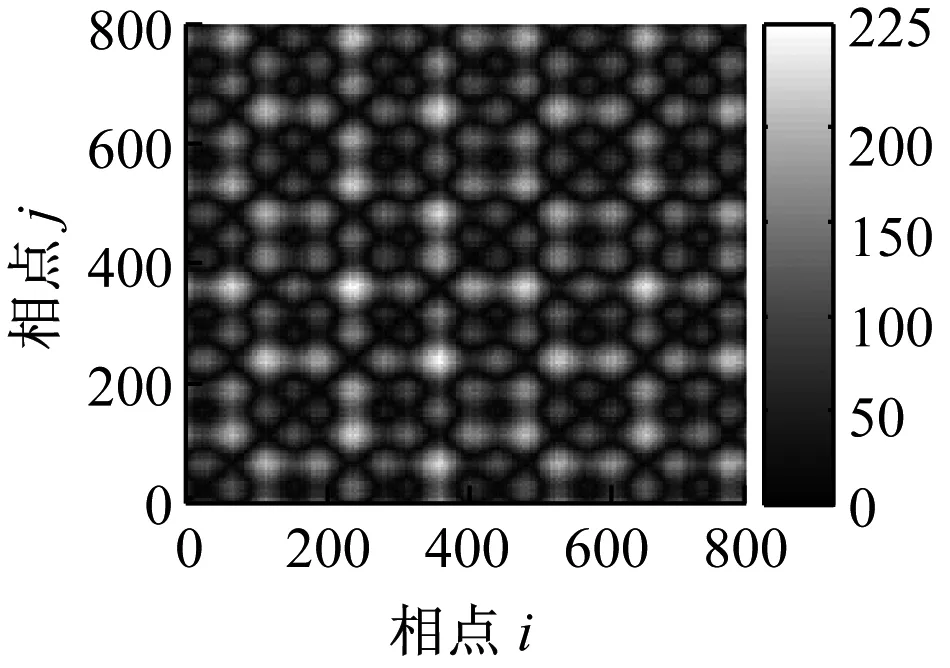
(d) 递归灰度图

显然，白噪声是完全平稳的，其递归图是均匀一致的；仿真信号存在局部阶段性的突变，其递归图基本不受噪声影响，大致类似。这是因为由于白噪声的平稳特性，其递归图是均布的，当信号中存在突变时，其递归图仍能在相应的在纹理上发生变化。但当r取不同值时，信号的递归图并不完全相同，主要体现在相应位置处纹理的多少不同，因此利用递归图对系统状态进行定性描述存在一定的不足，即阈值r的选取具有主观性。另外，当系统处于不同状态时，信号重构后的dmax、dmin均是不相同的，因此，如何确定阈值r就没有一个“公共”标准，使得递归图无法用于定量诊断。从图2和图3的递归灰度图可以看出，递归灰度图较递归图更充分的展现了点对之间的距离信息，更好的描述系统状态的复杂程度，且无需选择阈值，自适应性好，具有较强的噪声鲁棒性。

从递归图及递归灰度图的构造过程可知：递归图是递归灰度图的一个特例，即递归图是递归灰度图经过二值化阈值处理后所得到的，因此递归灰度图较之递归图更细致与精确。

2 双向二维主成分分析

如何对生成的图像进行特征提取，到目前为止还没有形成一个“针对何种图像，选用何种方法，提取何类特征”的统一认识。递 归 定 量 分 析方法(Recurrence Quantification Analysis, RQA)[12]的主要非线性特征量包括递归率、确定率、递归熵、分层率、平均对角线长度和递归次数等，但选取哪几个特征量需要人为进行判断；传统的图像特征提取方法需要进行图像特征指标的选择或是提取图像的单一特征量作为特征参数；以上方法或多或少都会引入人为因素或造成的重要的特征信息遗漏缺乏提取特征的自适应能力。TD2DPCA是由张道强等[13]提出的一种图像特征参数自适应提取方法，最早用于人脸识别中。本文将其引入轴承故障诊断中，使用TD2DPCA对生成的轴承振动信号递归灰度图进行自适应特征参数提取。

传统的2DPCA在特征提取上直接利用二维投影的方法，在图像的水平方向上进行运算，但是忽视了图像行中包含的相关性信息。TD2DPCA将行和列两种图像信息融合到一个判别分析框架中，识别率得到提高，同时计算复杂度较低[14-15]。

给定有C类模式:ω1,ω2,…,ωc，共M个训练样本图像：A1,A2,…,AM,每个样本大小为m×n。Gt为训练样本总体散度矩阵：

(6)

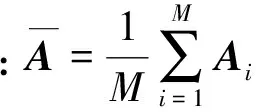
通过线性变换Y=AiX(i=1,2,…,k)将图像矩阵Ai投影至X上从而获得特征向量Y，其中X表示n维单位化的列向量。X为投影方向，其选取准则是使得投影后的特征向量具有更好的分类特性。定义准则函数

J(X)=tr(Gt)=XTGtX

(7)

式中：tr(Gt)为Gt的迹。

为了实现投影后得到的特征向量总体分散程度J(X)最大，需要寻找最优投影向量X。易证，Gt的最大特征值所对应的单位特征向量即为最优投影向量。因Gt为非负定矩阵，则存在n个标准正交的特征向量，假定

GtXi=Xi,(λ1≥λ2≥…≥λn≥0)

(8)

为了提高在多类样本情况下的区分性，单一的最优投影方向是不够的，因此取前d个最大特征值所对应的标准正交的特征向量作为最优投影矩阵P。假设P=[X1,X2,…,Xd]。对图像样本A，利用最优投影矩阵对其进行特征提取，获得相应的特征编码矩阵B，即B=AP。

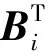
(9)

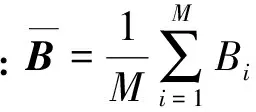
(10)

特征矩阵U的维数大小是h×d，相比于2DPCA只进行1次压缩提取的特征维数m×d，h要远小于m，从而进一步压缩特征维数，提高了后续分类效率。

3 轴承智能故障诊断流程

基于IRP与TD2DPCA的故障诊断方法对轴承的故障诊断，共分为以下几个步骤：首先对采集到的轴承振动信号生成递归图像，然后采用TD2DPCA方法对生成的递归图像进行特征参数提取，从中选取能够有效表征轴承工作状态的特征参数向量对分类器进行训练，用训练好的分类器对待分类特征参数进行分类识别，完成对轴承的故障诊断，方法步骤如图4所示。

4 轴承故障诊断实例

4.1轴承实验工况

依据实测轴承振动信号，来验证本文方法的可行性。采用某部队装备的变速箱轴承故障信号，故障轴承为6205型深沟球轴承。实验利用电火花在输出轴承的内圈沟道，外圈沟道和滚珠分别设置面积大约为2 mm2的点蚀，分别对应轴承内圈故障、外圈故障和滚动体故障，故障工况设置如表1所示。变速箱装置简图如图5所示，实际信号采集的传感器布置如图6所示。变速箱运行时，轴的转速大约为1 750 r/min(fr=29.17 Hz),负载为25 N·m，通过B&K3560数据采集仪采样，采样频率为1.2 kHz，滚动轴承振动信号采自变速箱轴承座的垂直振动信号。实验共采集轴承4种故障状态下各100种振动信号样本，总计400个，每个样本长度为825。

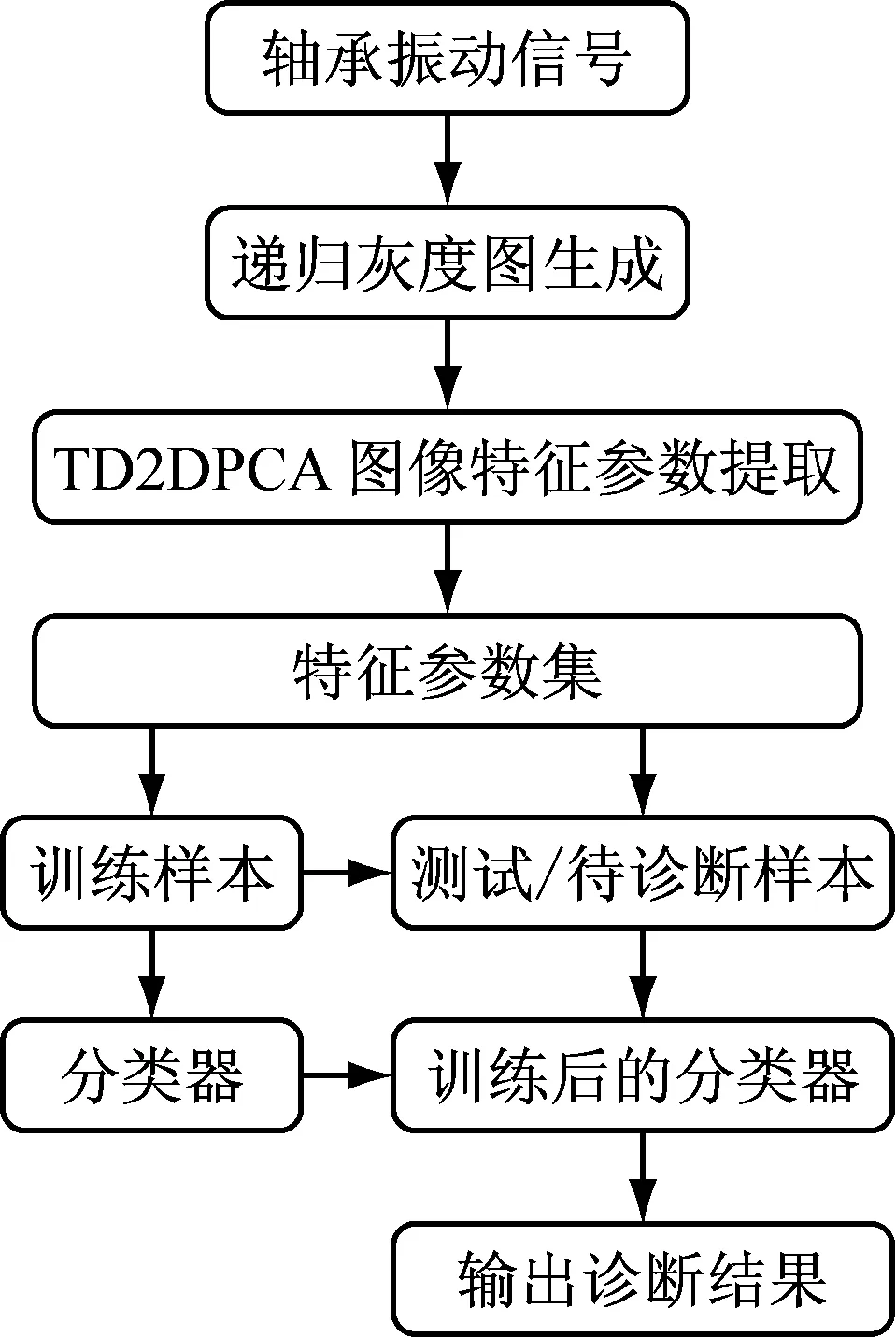
图4 基于IRP与TD2DPCA的故障诊断方法的步骤

故障部位1234内圈外圈滚珠否否否是否否否是否否否是

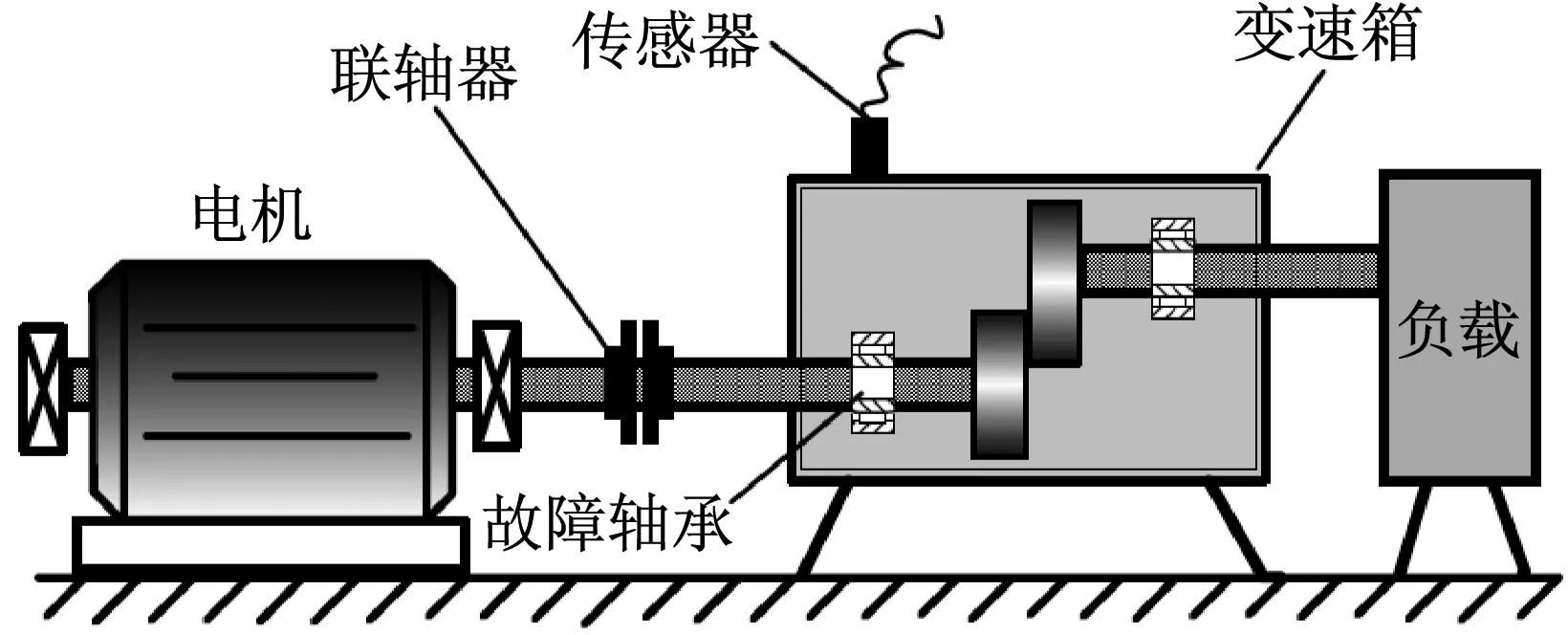
图5 变速箱装置简图

图6 传感器布置图

4.2轴承振动信号的递归图分析

取轴承4种工况下的振动信号，分别进行递归图和递归灰度图分析，并绘制其分布图，如图6～7所示。

图7所示为轴承4种不同工况下的递归图，该组图是经过多次尝试后选取的当阈值r=0.25×distmax时效果较好的递归图像。对比图7和图7可以看出，信号的递归图总体上类似，均能反映系统运行时的复杂程度，并有很好的噪声鲁棒性。较之图7，图8更充分地利用了系统相空间中的信息，点对之间的距离信息均得到了利用，所以递归灰度图对系统运行状态反映更全面。

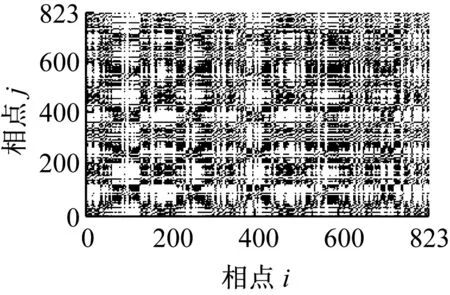
(a) 工况1

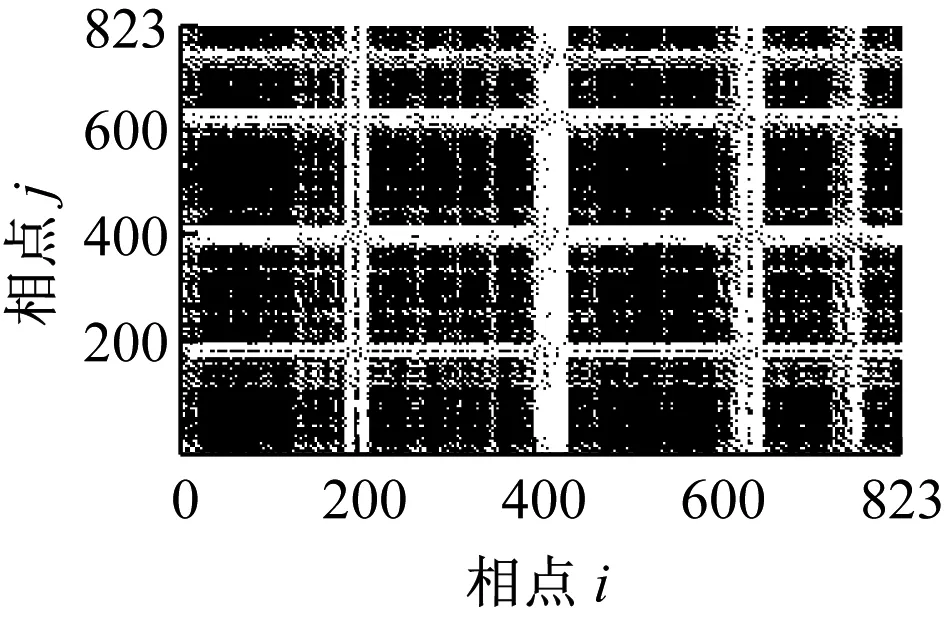
(b) 工况2

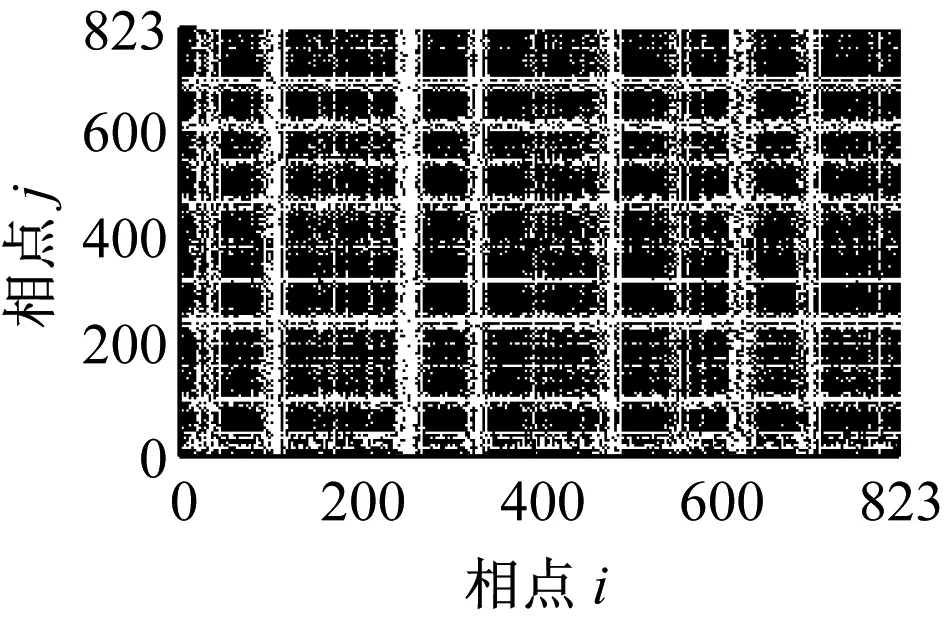
(c) 工况3

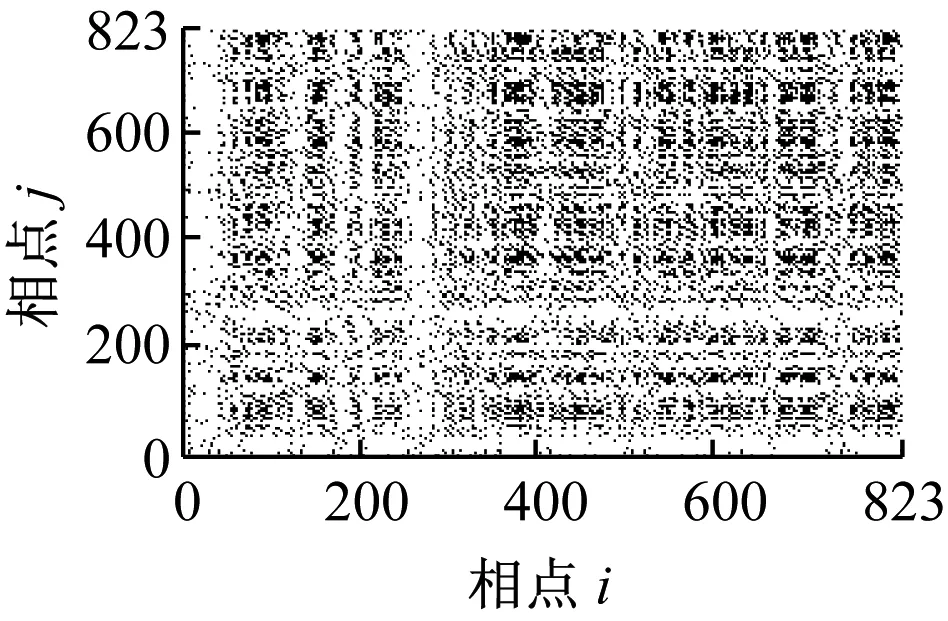
(d) 工况4

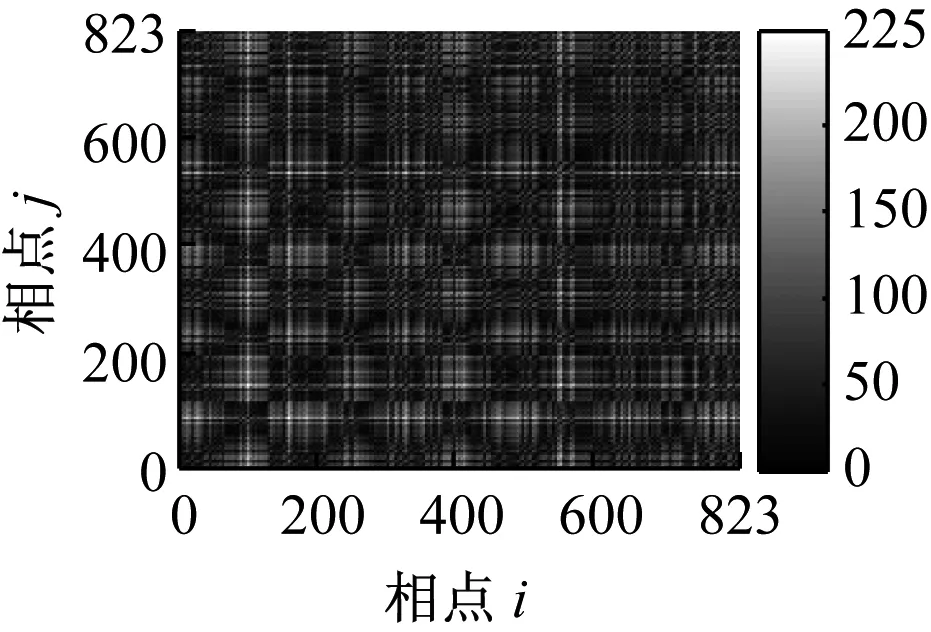
(a) 工况1

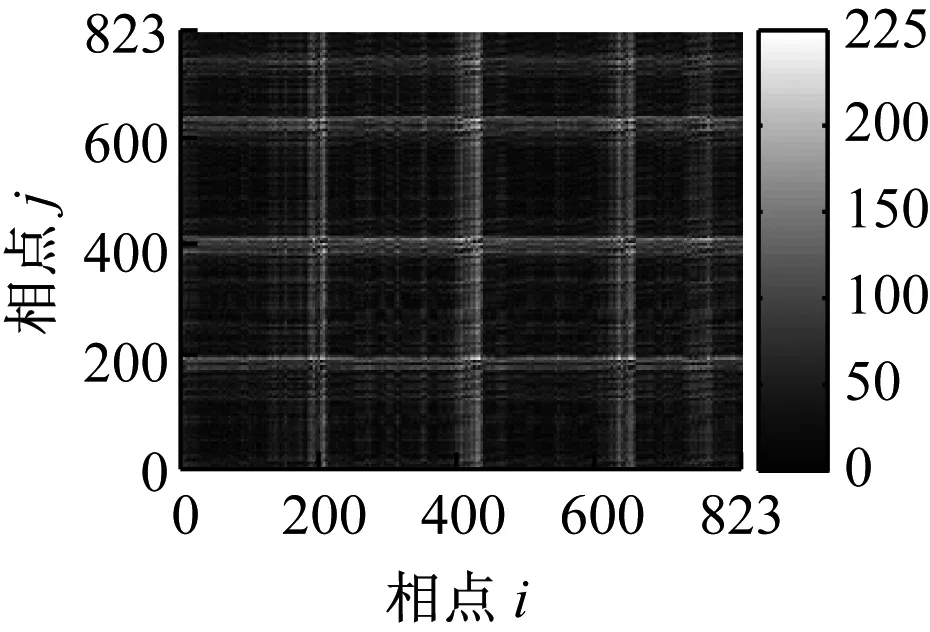
(b) 工况2

(c) 工况3

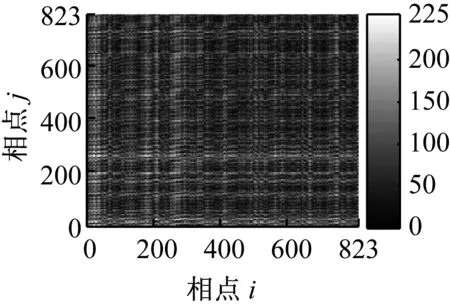
(d) 工况4

从递归灰度图中可以看到，轴承振动信号的递归灰度图对轴承的状态具有较好的反映能力，轴承处于不同状态时振动信号的递归灰度图具有明显的差别。工况1即正常状态时，递归灰度图没有显著的结构特征，表明系统存在多种结构的混叠，图中稀疏的浅色“十字”带状区域，表示系统存在阶段性的突变; 深色的水平或垂直线段说明该时间段内系统状态保持不变或变化缓慢。工况2即轴承内圈故障状态时，图中浅色“十字”带状结构将递归灰度图分割成多个矩形块，浅色“十字”带状结构面积明显增加，这是由于轴承内圈故障，周期性的冲击作用，系统中存在激烈的突变；工况3即轴承外圈故障状态时，图中浅色“十字”带状结构明显度下降，这表明轴承处于外圈故障时，外圈故障特征频率要小于内圈故障特征频率，系统的突变减少；工况4即轴承滚动体故障状态时，图中浅色“十字”带状结构此时已经不太明显，这是因为轴承滚动体故障特征频率相对较小，阶段性突进一步减少。由以上分析可知，递归灰度图用于描述轴承系统工作状态是有效的、可行的。

4.3IRP的TD2DPCA特征提取

IRP的TD2DPCA特征参数提取流程如下:

步骤1 取采集到的N个信号作为研究对象并分别绘制递归灰度图，相应得到N个823×823像素点的时频矩阵。

步骤2 从四类工况的递归灰度图中，每一类随机选取M(M≤N)幅，共200幅组成TD2DPCA样本集T;

步骤3 对样本集T进行TD2DPCA特征提取，得到最优投影矩阵P823×d和Q823×h。d和h分别表示两次提取的特征维数，它的取值对特征提取结果和后续的识别精度有较大影响;

步骤4 将所有的递归灰度图像向矩阵P和Q投影，可得其对应得编码矩阵H，维数为h×d，共有N个H。每一个编码矩阵H代表了它所对应的递归灰度图像;

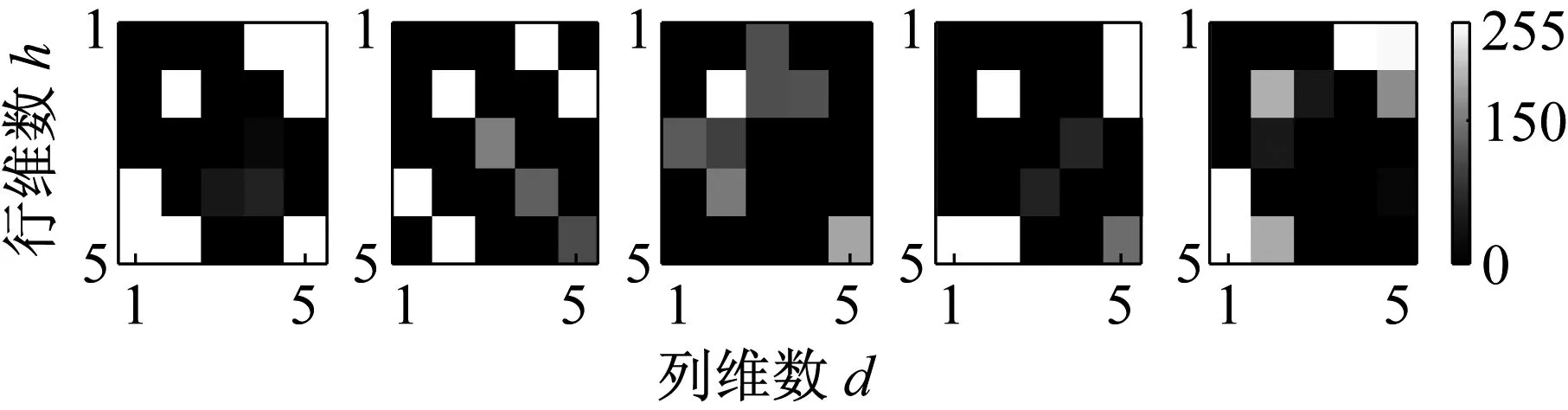
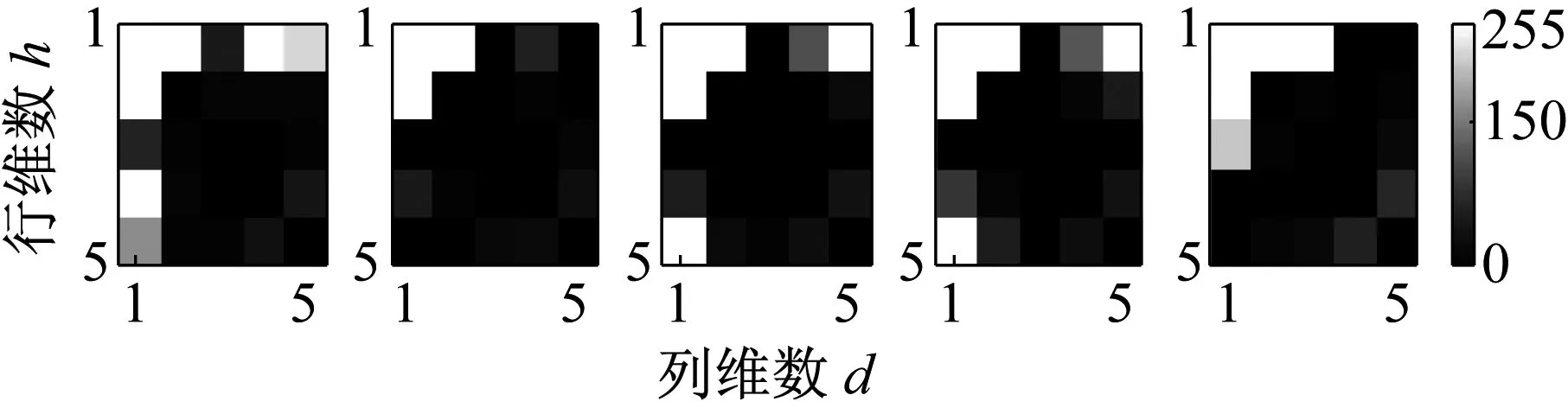
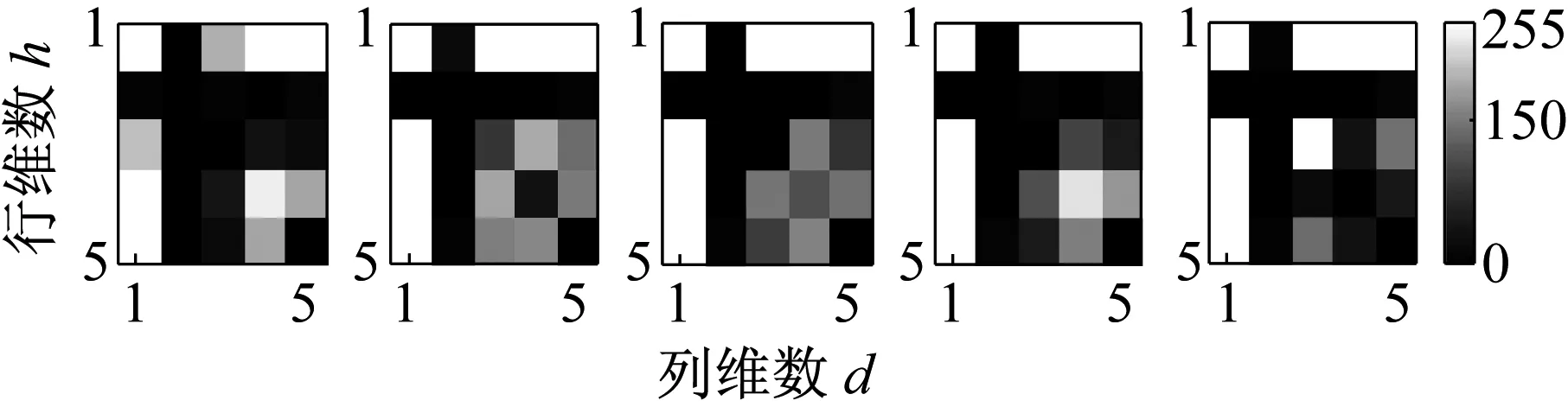
图9给出的是特征维数h×d=5×5时，递归灰度图像训练集对应的特征系数H，图中每个像素的灰度值严格与样本系数H的值一一对应，文章篇幅有限，每种工况下选取5个H显示。图中每一行代表一种轴承工况，从上到下依次为轴承正常、轴承内圈故障、轴承外圈故障和轴承滚动体故障。从图中可以看出TD2DPCA对数据进行了非常有效的降维，将823×823维数据压缩到5×5维，大大降低了识别复杂度和计算量；并且同种工况编码矩阵像素灰度值较为相似，不同工况间区别较大，有利于下一步的分类识别。

4.4故障识别

在对内轴承工况进行分类时，本文选取最近邻分类器(KNNC)作为轴承工况判别的智能学习机器。从四类工况中每一类中随机选出50个编码矩阵H共200个，组成训练样本集合。然后用剩余的200个系数向量进行分类测试，重复以上实验10次取平均值。用识别正确率作为指标来评价文中方法的性能。

为进一步表明文中提出的基于IRP和TD2DPCA的轴承故障诊断方法的可行性与有效性，采用对比的方法，分别令r1=0.2×distmax，r2=0.4×distmax，r3=0.6×distmax对采集到的信号进行递归图生成，采用 TD-2DPCA对上述得到的图像进行特征参数提取，2次提取的特征维数分别为d×h=[2×2,3×3,…，10×10]，采用最近邻分类器对上述特征参数进行识别和工况分类，重复实验过程10次，分类精度如图10所示。

(a) 工况1

(b) 工况2

(c) 工况3

(d) 工况4

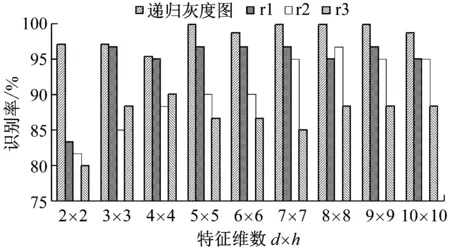
图10 IRP与RP方法识别率对比

从图10中可以看出，使用RP方法对轴承振动信号进行递归图生成，随阈值r的取值不同其识别率也各不相同，当r1=0.2×distmax平均识别精度较高，最高识别精度可达96.67%，随着阈值的增加，平均识别精度有所下降。这是因为，当r取值过小或取值过大生成的递归图像都不能充分反映系统的复杂度，两种情况均不利于分类识别。阈值r取值的不同，生成的递归图也会随之相应变化，因此利用递归图进行轴承故障诊断受主观人为因素影响较大。轴承振动信号的递归灰度图较之递归图更加细致与精确，能较好对系统的复杂程度进行反映，且每一个振动信号，对应唯一的递归灰度图，因此将递归灰度图用于描述轴承系统状态的复杂程度是非常有效的，在不同特征维度下其识别精度均保持了较高水平，最高可达99.80%。对轴承的4类工况诊断结果表明，TD2DPCA在对图像进行特征参数提取过程中，轴承故障识别精度对特征维数的大小变化并不敏感，在特征维数较小时，仍具有较高的识别精度。因此在利用TD2DPCA对图像进行特征参数提取时，可根据故障诊断的具体需求合理设定特征维数。

5 结 论

(1) 针对递归图中阈值选取问题进行了改进，提出了递归灰度图算法。较之递归图，递归灰度图能充分反映系统的相空间信息，对轴承系统运行状态反映更全面细致，无需设定阈值，自适应性和噪声鲁棒性好。

(2) 用TD2DPCA方法对4种典型轴承工况递归灰度图进行特征参数提取,有效避免了在利用图像分析技术进行特征参数提取时不同图像特征指标的选择问题造成的重要信息的遗漏，可对不同工况的递归灰度图像自适应地计算特征参数，数据降维效果明显。

(3) 对比分析了基于RP和TD2DPCA轴承故障诊断方法与基于IRP和TD2DPCA的轴承故障诊断方法。结果表明，基于IRP和TD2DPCA的轴承故障诊断方法故障识别精度更高，自适应性更好，适用于轴承故障诊断。

[1] 唐贵基，王晓龙. 参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J].西安交通大学学报，2015，49(5)：73-80.

TANG Guiji, WANG Xiaolong. Parameter optimized variational mode decomposition method with application to incipient fault diagnosis of rolling bearing[J].Journal of Xi’an JiaoTong University, 2015，49(5)：73-80.

[2] 丁建明,林建辉,任愈,等. 基于谐波小波包能量熵的轴承故障实时诊断[J] .机械强度,2011,33(4):483-487.

DING Jianming, LIN Jianhui, REN Yu,et al. Real-time diagnosis of bearing faults based on harmonic wavelet energy entropy [J]. Journal of Mechanical Strengh, 2011，33(4)：483-487．

[3] 李学军，何能胜，何宽芳. 基于小波包近似熵和SVM的圆柱滚子轴承诊断[J]. 振动、测试与诊断，2015, 35(6): 1031-1036.

LI Xuejun, HE Nengsheng, HE Kuanfang. Cylindrical roller bearing diagnosis based on wavelet packet approximate entropy and support vector machines [J]. Journal of Vibration, Measurement&Diagnosis, 2011, 35(6): 1031-1036.

[4] 程发斌，汤宝平，刘文艺. 一种抑制维格纳分布交叉项的方法及在故障诊断中应用[J]. 中国机械工程，2008，19(14)1727-1731.

CHENG Fabin,TANG Baoping,LIU Wenyi. A method to suppress cross-terms of wigner-ville distribution and Its application in fault diagnosis [J]. China Mechanical Engineering, 2008，19(14):1727-1731.

[5] 蔡艳平，李艾华，石林锁，等. 基于EMD与谱峭度的滚动轴承故障检测改进包络谱分析[J].振动与冲击， 2011，30(2): 167-172.

CAI Yanping, LI Aihua, SHI Linsuo,et al.Roller bearing fault detection using improved envelope spectrum analysis based on EMD and spectrum kurtosis[J]. Journal of Vibration and Shock, 2011，30(2)：167-172．

[6] ECKMANN J P, KAMPHORST S O, RUELLE D. Recurrence plots of dynamical systems [J]. Europhys Lett, 1987(5): 973-977.

[7] 蒲晓川，肖涵. 基于EMD降噪的递归图分析方法在齿轮故障诊断中的应用[J].机床与液压， 2015，43(5): 160-163.

PU Xiaochuan, XIAO Han. Application of recurrence plot analysis method to fault diagnosis based on EMD [J]. Machine Tool & Hydraulics, 2015，43(5)：160-163．

[8] 潘玉荣，贾朝勇.基于递归图的电价信号复杂度描述[J]. 洛阳师范学院学报,2013,32(2):11-16.

PAN Yurong, JIA Chaoyong. Complexity description of power price signals based on methods of recurrence plots [J]. Journal of Luoyang Normal University, 2013, 32(2): 11-16.

[9] 刘秉正，彭建华．非线性动力学[M]．北京：高等教育出版社，2003.

[10] 关贞珍，郑海起，杨云涛,等．某型滚动轴承故障与分形维数的确定[J]．机械科学与技术，2009，28 (9)：1147-1152．

GUAN Zhenzhen, ZHENG Haiqi, YANG Yuntao, et al. Fault diagnosis of a bearing based on chaos and fractal theory[J]. Mechanical Science and Technology for Aerospace Engineering, 2009,28(9):1147-1152．

[11] 夏勇，薛扬，罗晓春，等. 内燃机振动信号复杂度的定性描述[J]. 机械,2003,30(4):51-53.

XIA Yong, XUE Yang, LUO Xiaochun,et al. Qualitative description for the vibration signals of internal combustion engines [J]. Machine, 2003, 30(4): 51-53.

[12] 张淑清，包红燕，李盼，等. 基于RQA与GG聚类的滚动轴承故障识别[J]. 中国机械工程,2015,26(10):1384-1389.

ZHANG Shuqing, BAO Hongyan, LI Pan,et al. Fault diagnosis of rolling bearings based on RQA and GG clustering [J]. The Chinese Mechanical Engineering, 2015, 26(10): 1384-1389.

[13] ZHANG Daoqiang, ZHOU Zhihua. (2D) 2PCA: Tow-directional tow-dimensional PCA for efficient face representation and Recognition[J]. Neuro computing, 2005, 69(1/2/3): 224-231.

[14] YANG J,ZHANG D,FRANGI A F,et al. Two-dimensional PCA: a new approach to appearance-based face representation and recognition[J].Pattern Analysis and Machine Intelligence, 2004, 26(1):131-137.

[15] 李巍华，林龙，单外平．基于广义S变换与双向2DPCA的轴承故障诊断[J]．振动、测试与诊断，2015，35(3)：499-506．

LI Weihua,LIN Long,SHAN Waiping. Engine vibration time-frequency analysis based on EMD-Wigner-Ville[J]. Journal of Vibration, Measurement&Diagnosis, 2015，35(3)：499-506．

RollerbearingfaultdiagnosisbyusingIRPandTD2DPCA

YUEYingjuan1,SUNGang1,CAIYanping2,WANGXinjun2

(1. Science College of Rocket Force Engineering University，Xi’an 710025 China； 2. Five Department of Rocket Force Engineering University，Xi’an 710025 China)

The vibration signals of bearings are usually non-stationary and it is difficult to extract the fault parameters in reality. A fault diagnosis method was proposed based on the Improved Recurrence Plots(IRP) and Two directional Two dimensional Principal Component Analysis(TD2DPCA). For selecting and optimizing the Recurrence Plots(RP) threshold, the IRP was applied in bearing vibration acceleration signals to obtain IRP images. On this basis, in order to get parameters code matrixes, the TD-2DPCA was used to process the bearing IRP images. A classifier was then used to the code matrixes for pattern recognition so as to realize the automatic diagnosis of bearing IRP images. The proposed method has been used in four kinds of bearing vibration signals and the fault diagnosis accuracy is up to 100%. The results show that: the roller bearing fault diagnosis method using the IRP and TD2DPCA has the ability of adaptive bearing fault diagnosis, and is of good recognition accuracy and noise robustness, which explores a new way for the bearing vibration diagnosis.

bearing; recurrence plots; improved recurrence plots; two directional two dimensional principal component analysis; fault diagnosis

TK418；TN911.6

A

10.13465/j.cnki.jvs.2017.21.001

国家自然科学基金(51405498)；陕西省自然科学基金(2013JQ8023)；中国博士后基金(2015M582642)

2016-05-10 修改稿收到日期：2016-07-27

岳应娟 女,博士,教授,1973年生

孙钢 男,硕士,1989年生