多级多悬挂设备对高速列车垂向振动影响研究

贺小龙， 张立民， 鲁连涛， 周 辉

(西南交通大学 牵引动力国家重点实验室，成都 610031)

多级多悬挂设备对高速列车垂向振动影响研究

贺小龙， 张立民， 鲁连涛， 周 辉

(西南交通大学 牵引动力国家重点实验室，成都 610031)

为了研究设备以单级、双层形式悬挂对高速列车垂向振动的影响，建立了车辆-设备刚柔耦合模型，获得了车体中部、构架上方以及设备的加速度频响函数。考虑几何滤波效应，设备的连接方式(刚性、弹性)、连接刚度、连接位置等因素下车体与设备的耦合振动特性以及其相互影响关系。结果表明：速度作为几何滤波效应的影响因素，在研究车辆-设备耦合振动时必须考虑速度的影响；车辆在6～12 Hz内的振动响应受设备连接参数影响明显；在双层隔振系统中，框架更容易与车体产生耦合振动；当设备连接刚度为原始值时，车体中部响应较小，但双层隔振系统中设备会与框架产生耦合振动导致二者振动急剧增大；设备连接位置越靠近车体中部，车体的低阶垂向弯曲模态更易解耦，可以显著降低车体中部振动，同时使得车体的高阶垂弯频率最大提高0.4 Hz。

多级多设备；加速度频响函数；几何滤波效应；弹性连接参数；安装位置

轻量化技术在在铝合金车体上的广泛运用使得车体的质量越来越轻，弹性越来越强，当受到线路激扰时更容易引起车体振动[1]。近几年，随着EMU(Electric Multiple Unit)模式在车辆制造业中普及，越来越多设备悬挂在车体底架下，这些设备质量从几十千克到几吨不等，有的甚至自带激励源，在一定程度上影响了车辆的振动[2]。如今，多级多设备的悬挂布局形式在高速动车组中十分常见，即多个设备以单层、双层、刚性、弹性形式悬挂于车体底架下。罗光兵等[3-5]对于多悬挂设备的车体振动特性进行研究时，大多停留在有限元或者仿真计算层面，缺乏理论计算依据[6]。对此，建立了车体-多设备的27自由度的刚柔耦合数学模型，获得了车体中部、构架上方、设备和框架的加速度频率响应函数表达式，研究了多级多悬挂设备对高速列车车体垂向振动的影响规律。考虑几何滤波效应，车辆运行速度、设备连接刚度、连接位置等因素对车辆和设备的垂向振动的影响，研究结论可以为车下设备的安装设计提供指导。

1 车辆-设备耦合动力学模型

车辆-设备系统垂向模型如图1所示[7]。本文所研究的车辆系统包含一个车体，两个构架，四个轮对，一个单层悬挂系统，一个双层设备悬挂系统。车辆运行速度为V，并且假设轮轨完全接触。将车体考虑成欧拉-伯努利梁，具有均匀分布质量，考虑车体的一阶垂向弯曲模态。梁的长度为L；ρ=M/L为车体单位长度的质量；μ为车体结构阻尼系数；EI为车体的抗弯刚度。考虑车体的沉浮Z、点头θ、一阶垂向弯曲振动X；考虑构架的沉浮Z，点头θ，纵移Xbi(i=1,2)；考虑设备的沉浮Z，点头θei(i=1,2,3)；考虑轮对的沉浮Z0i，纵移X0i(i=1,2,3,4)；钢轨的垂向位移ηi(i=1,2,3,4)。其中车体的位移w(x,t)为车体的刚体振动与弹性弯曲振动的叠加[8-9]

w(x,t)=zc(t)+(x-2/L)θC(t)+X2(x)T2(t)

(1)

图1 车辆设备耦合系统垂向动力学模型Fig.1 The verticalmechanical model of the vehicle-equipment coupling system

本文中数值计算参数，如表1所示。

表1 车辆计算参数

2 车辆-设备运动方程

图1中，车体的振动方程为[10]

(2)

式中：δ(x)为狄克拉函数；li为二系支撑位置；lei为设备悬挂位置；Fzci为二系支撑力；Fzei为设备作用在车体上的力；Mci、Fxci为构架作用在车体上的力矩和纵向力。

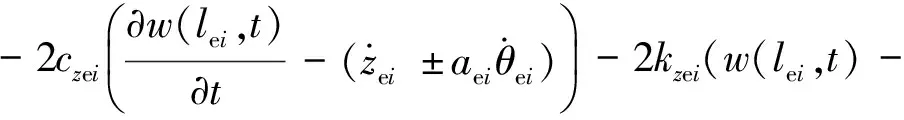
构架的沉浮运动方程为

(3)

构架的点头运动方程为(i=1,2)

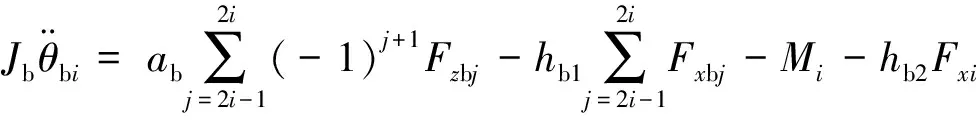
构架的纵移运动方程

(5)

2kzb(zbi±abθbi-z0j,(j+1))。

设备1沉浮运动方程为

(6)

设备1点头运动方程

(7)

框架的沉浮运动方程为

2kze3(2ze3-2ze2)=0

(8)

框架的点头运动方程为

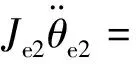
2kze3ae2(ze3-ze2+ae3θe3-ae2θe2)=0

(9)

设备2沉浮运动方程为

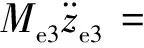
2kze3(ze3-ze2+ae3θe3-ae2θe2)

(10)

设备2点头运动方程

2kze3ae3(ze3-ze2+ae3θe3-ae2θe2)

(11)

轮对的纵移方程，其中j=2i-1,i=1,2

(12)

轮对的沉浮运动方程

(13)

式中：ΔQj,(j+1)=-kH[z0j,(j+1)-zsj,(j+1)-ηj,(j+1)]；j=2i-1,i=1,2；kH为轮轨接触刚度；ηj,(j+1)为轨道高低不平顺值。对于轨道的垂向运动方程为

(14)

3 车辆系统频响函数方程

车辆系统方程可以表示为[11]

(15)

式中：[M]、[C]、[K]分别为质量、阻尼和刚度矩阵；y为车辆系统中各自由度的响应，对式(15)进行变换，可以得到车辆系统加速度频率响应函数为

Ha(ω)=-ω2[-ω2[M]+iω[C]+[K]]-1[[Dw]+iω[Ddw]]

(16)

式中，下标a为加速度响应，车辆系统为多输入多输出系统，考虑轮对激励的时间滞后特性，可以将多输入多输出系统转换为单输入多输出系统，其转换表达式为

(17)

式中：η1(ω)为轮对1激励函数；ti为其余轮对滞后时间；t1=2ab/V，t2=2aC/V,t3=2(aC+ab)/V。

由此，车体上任意位置x处的频率响应函数Hc(ω,x)为

Hc(ω,x)=Hzc(ω)+(x-L/2)Hθc(ω)+Xn(x)HT2(w)(18)

车体中部的加速度响应为

Hc(L/2,w)=Hzc(ω)+X2(L/2)HT2(ω)

(19)

转向架上方(一位端、二位端)加速度响应为

Hc(l1,2，w)=Hzc(ω)±aCHθC(ω)+X2(l1,2)HT2(ω)

(20)

4 数值计算结果分析

图2为无设备连接、设备刚性连接和设备弹性连接条件下车体中部(见图2(a))、车体一位端转向架上方图2(b)的加速度频域响应函数曲线。图2在1.2 Hz处出现的峰值对应于车体的沉浮模态，车体的刚体振动这里不讨论。图中车体的垂向弯曲频率随着设备的吊挂方式不同而改变：无设备时，车体的垂向弯曲频率为10.2 Hz；设备刚性连接时，垂向弯曲频率为9.3 Hz；多级多设备弹性连接时，车体的垂向弯曲频率为6.4 Hz，7.8 Hz，10.7 Hz，其中6.4 Hz、7.8 Hz为因悬挂两个设备引起的车体垂向弯曲振动频率，10.7 Hz为车体自身的垂向弯曲振动频率，文中统一称呼为高阶垂向弯曲频率。设备连接方式不同对车体的振动幅值发生变化：设备刚性连接使车体中部振动幅值减小，车体构架上方振动幅值增加；设备弹性悬挂后，车体在之前垂弯频率处不再出现峰值，取而代之的是两个低频峰值和一个高频峰值，车体的振动也有很大衰减。

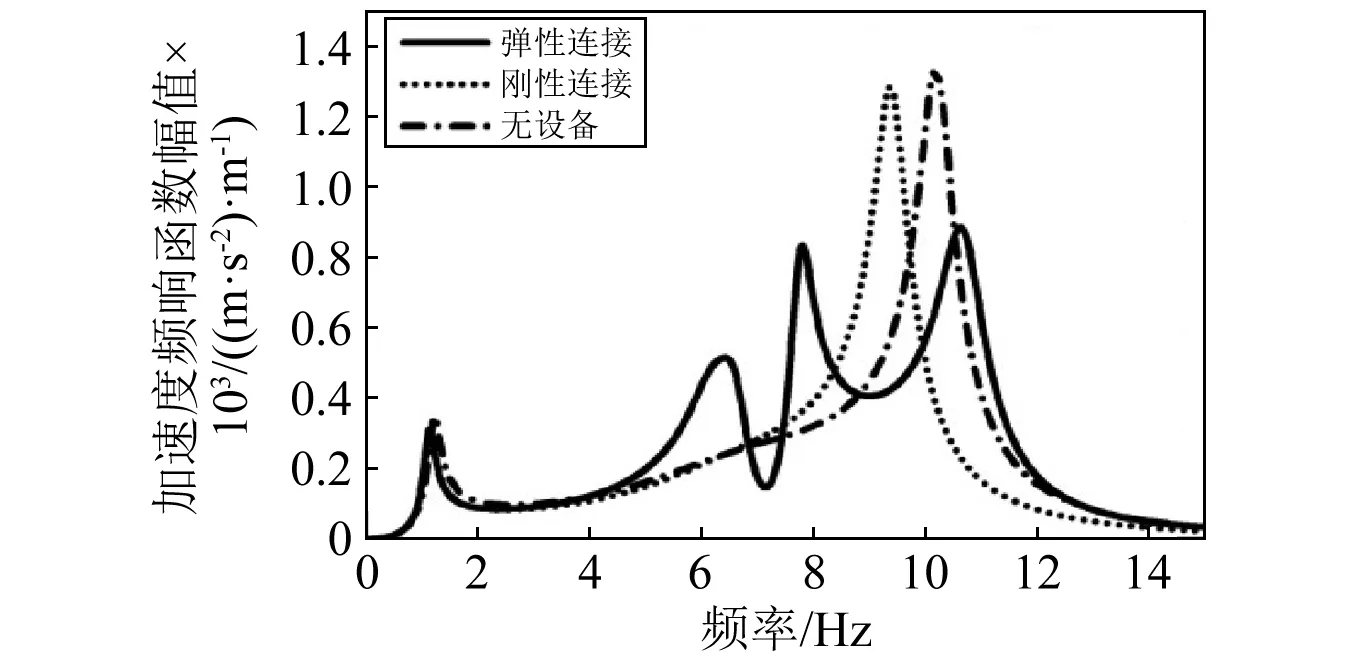
(a) 车体中部加速度响应

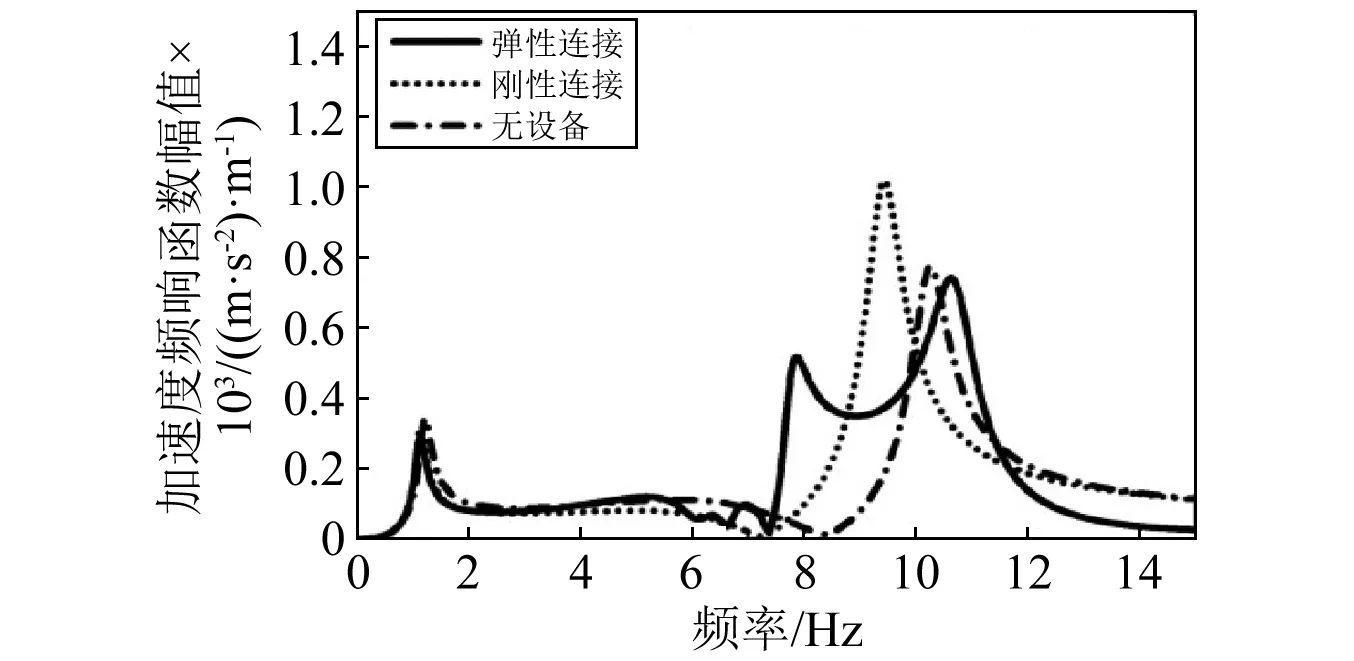
(b) 车体端部加速度响应图2 设备不同连接条件下车体加速度响应Fig.2 Acceleration frequency response of car body

车辆在实际运行中，轨道不平顺的垂向激励存在时间滞后，其滞后常数由车辆定距，轴距和车辆行驶速度共同决定。在与悬挂系统共同作用下，会产生车体或者车体某阶阵型对轨道某些不平顺波长没有响应的现象，这一现象称为“几何滤波效应”[12]，滤波频率计算如式(21)所示

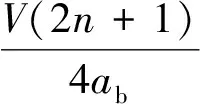
(21)

式中：n=0,1,2，…；在f1频率下，车体将没有点头和沉浮响应；f2频率下，车体沉浮响应为0；f3频率下，车体的点头响应为0。车辆行驶速度为250 km/h、350 km/h，其滤波频率计算结果如表2所示。

图3、图4分别为车辆在时速250 km/h、350 km/h车体中部和构架上方的加速度响应函数。由图可知，由于几何滤波效应的影响，车体三个参考点的振动响应会出现一连串的极大值和极小值。出现极值处频率基本与表2中的滤波频率吻合：两种速度下，点头滤波频率(f3)在车体中部响应中均未出现极值，这与实际情况相符。图3(a)在1.98 Hz下，图4(a)在2.78 Hz下，车体中部响应为0，说明车体中部响应在低频下以沉浮振动为主；而一位构架、二位构架上方响应不为0，说明在低频下构架上方振动以车体点头模态为主。图3中设备弹性连接在5.95 Hz、7.94 Hz、9.92 Hz、11.9 Hz频率处，图4中设备弹性连接在5.56 Hz、8.33 Hz、11.11 Hz频率处，车体中部和构架上方振动响应均不为0，由此可知：在4～12Hz内，车体的振动响应主要来源于车体的弹性振动和车体与设备弹性连接产生的耦合振动，在该频段几何滤波效应的影响相对较弱。

表2 滤波频率

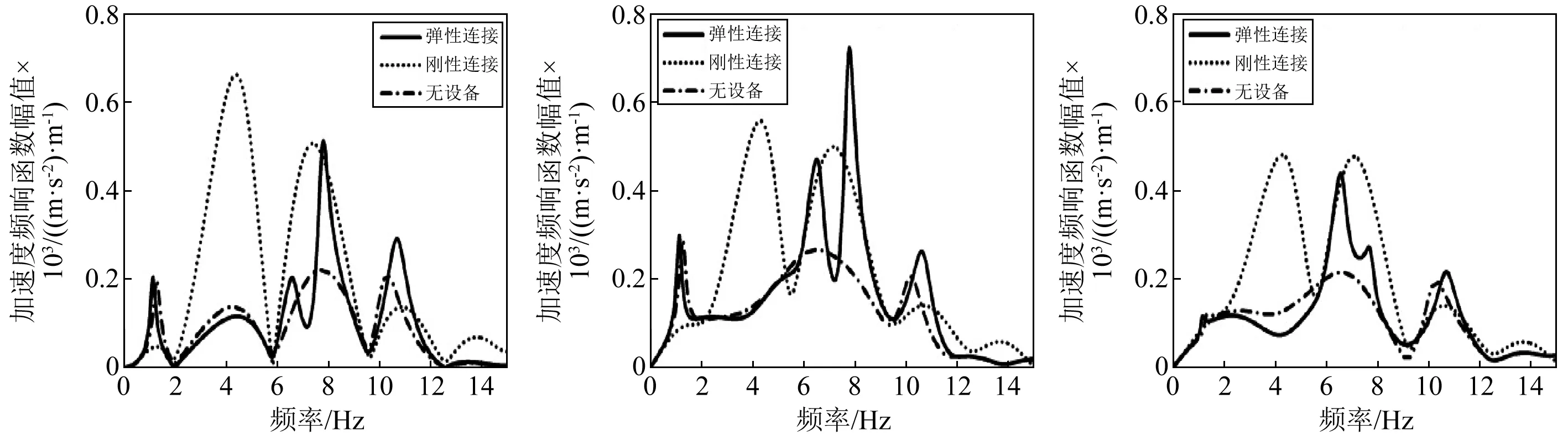
(a)车体中部 (b)一位端构架上方 (c)二位端构架上方图3 时速250 km/h车体响应Fig.3 Acceleration frequency response of car body under 250 km/h

与350 km/h条件下车体响应相比，250 km/h时几何滤波效应更为明显，车辆的运行速度对车体振动响应有很重要影响。与设备刚性连接相比，设备弹性连接能在一定程度降低车体的振动，但是在车体的高阶垂向弯曲频率处(10.7 Hz)，设备弹性连接时车体振动比刚性连接大，这是由于设备刚性连接使得车体在低频模态频率处振动能量较大，从而衰减了车体在弹性模态频率处的振动能量。

图5～图7为设备1、框架、设备2连接刚度在0.1Kei～20Kei(i=1,2,3)内变化对车体中部振动响应的影响，计算条件为le1=14.75 m，le1=9.25 m。

(a)车体中部 (b)一位端构架上方 (c)二位端构架上方图4 时速350 km/h车体响应Fig.4 Acceleration frequency response of car body under 350 km/h

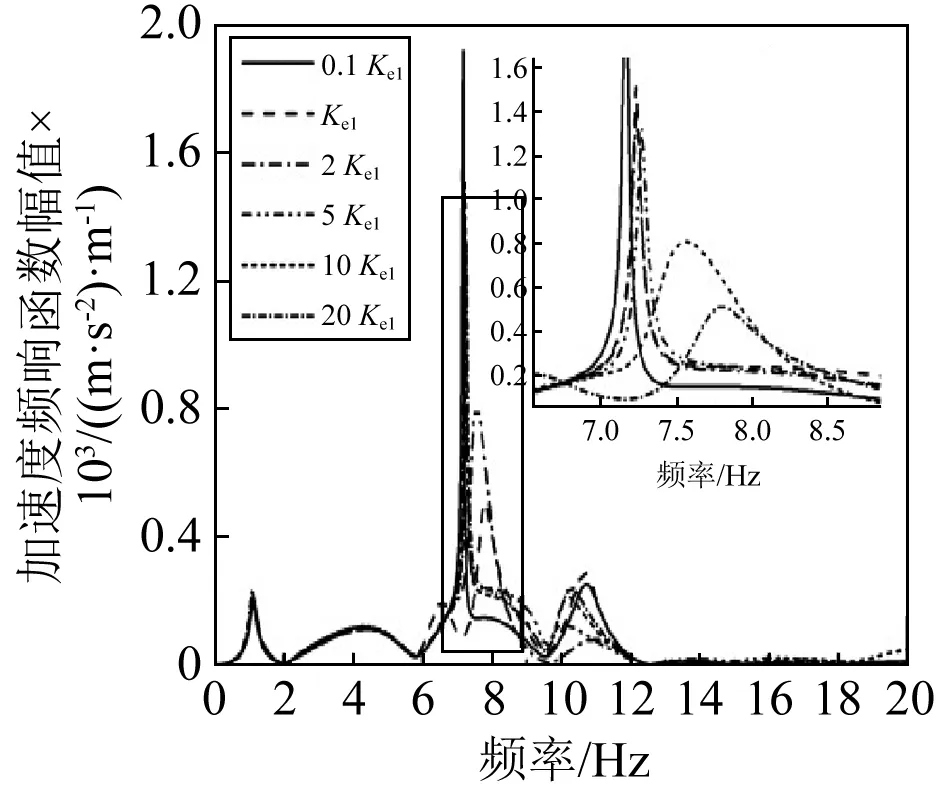
图5 设备1 连接刚度对车体中部响应影响Fig． 5 The influence of equipment 1 connecting stiffness on middle vehicle

图6 框架连接刚度对车体中部响应影响Fig． 6 The influence of frame connecting stiffness on middle vehicle

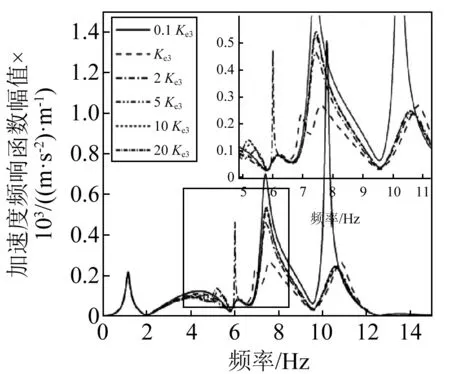
图7 设备2 连接刚度对车体中部响应影响Fig． 7 The influence of equipment 2 connecting stiffness on middle vehicle stiffness on middle vehicle connecting stiffness on middle vehicle

由图5可知，设备1连接刚度的改变主要影响车体中部在6～12 Hz内的响应，车体响应最大振幅在0.1Ke1时取得：1 925 (m/s2)/m；车体响应最小振幅在1Ke1时取得：500 (m/s2)/m；车体的高阶垂向弯曲模态频率主要在10～10.7 Hz内变化。除1Ke1外，其余连接刚度条件下，车体两阶垂向弯曲模态会发生耦合振动，产生一个较大峰值，这种情况在0.1Ke1、5Ke1、10Ke1、20Ke1最为明显，四种连接刚度下峰值依次降低。1Ke1与2Ke1条件下车体中部峰值变化不大，唯一区别在于1Ke1时车体前两阶垂向弯曲模态未产生耦合振动，解耦程度较高，振动能量分别分布到两阶模态上。

同理，框架的连接刚度(见图6)主要影响车体中部在6～12 Hz频段内的响应，车体响应最大振幅在2Ke1时取得：777 (m/s2)/m；车体响应最小振幅在1Ke1时取得：262 (m/s2)/m；车体的高阶垂向弯曲模态频率变化范围为9.8～10.9 Hz。除1Ke1以外，其余连接刚度下车体前两阶垂向弯曲模态均产生耦合振动，在7～9.5 Hz内只产生一个较大峰值，并且峰值随着2Ke1、5Ke1、0.1Ke1、10Ke1、20Ke1连接刚度变化逐渐降低。

图7中，在设备2的6种连接刚度中，0.1Ke1对车体响应影响最大，此时车体在两个固有频率处均取得最大值：695 (m/s2)/m,1 358 (m/s2)/m。设备2连接刚度的变化对车体高阶垂向弯曲频率影响不大。同样只有在1Ke1时，车体前两阶垂向弯曲模态未发生耦合振动。注意到图中在2Ke1下，在6.0 Hz处产生较大峰值，对比分析可知，该频率对应为框架的沉浮频率，该条件下，框架的垂向振动较大。

综上所述，设备1、框架、设备2吊挂刚度为1Kei(i=1,2,3)时，三阶垂向弯曲模态解耦程度较高，车体中部振动幅度较小，从车体振动控制角度来看，该吊挂刚度属于较优吊挂刚度。

图8为框架连接刚度变化对框架沉浮和点头模态、设备2沉浮和点头模态响应的影响。6种连接刚度下，框架和设备的4阶模态均在7.4 Hz处出现峰值，该峰值频率对应于框架沉浮和点头耦合振动频率；其中，在1Ke2时振动最大，其余5种连接刚度下，振动幅值均较小；框架的振动较设备2振动大。因为框架连接着设备2和车体，各阶模态容易发生耦合振动，导致图8中响应在6～12 Hz内模态未能很好解耦。对比图6和图8发现，当车体振动较小时(如1Ke2条件下)，框架和设备振动较大；当框架和设备振动较大时，车体振动就较小。

(a) (b) (c) (d) 图8 框架连接刚度对框架和设备振动影响Fig.8 The influence of frame connecting stiffness on frame and equipment 2

图9为设备2连接刚度变化时框架沉浮、点头，设备2沉浮、点头响应特性。因设备2只和框架连接，所以相比框架振动，设备2的模态更容易解耦。正如图9中所示，6种连接刚度下，设备2的模态峰值轮廓清晰，峰值明显；且随着刚度增大，振动能量逐渐向低阶模态聚集，这种现象在框架上并没有。同时注意到1Ke3时，在7.4 Hz处框架、设备2振动较大，这是框架沉浮、点头模态发生耦合振动所致。2Ke3时，在6.0 Hz处产生较大峰值；0.1Ke3时，在车体高阶垂向弯曲频率处产生较大峰值。

(a) (b) (c) (d) 图9 设备2连接刚度对框架和设备振动影响Fig.9 The influence of equipment 2 connecting stiffness on frame and equipment 2

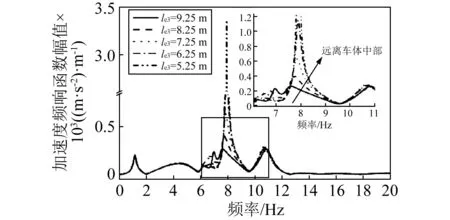
图10 设备1连接位置对车体中部振动影响Fig.10 The influence of equipment 1 connecting position on center vehicle

图10为设备1连接位置变化对车体中部响应影响。随着设备1逐渐远离车体中部，车体在第2阶垂向弯曲模态频率处的振动逐渐增大，同时车体前两阶垂弯频率带宽逐渐增大。图11为框架连接位置对车体中部振动影响。由图11可知：当lel≤117.75 m时，车体在框架系统的两阶模态频率处不会发生耦合振动，随着框架系统远离车体中部，车体中部响应随之增大。同时计算发现，无论是设备1还是框架系统远离车体中部，其自身振动都会逐渐增大。

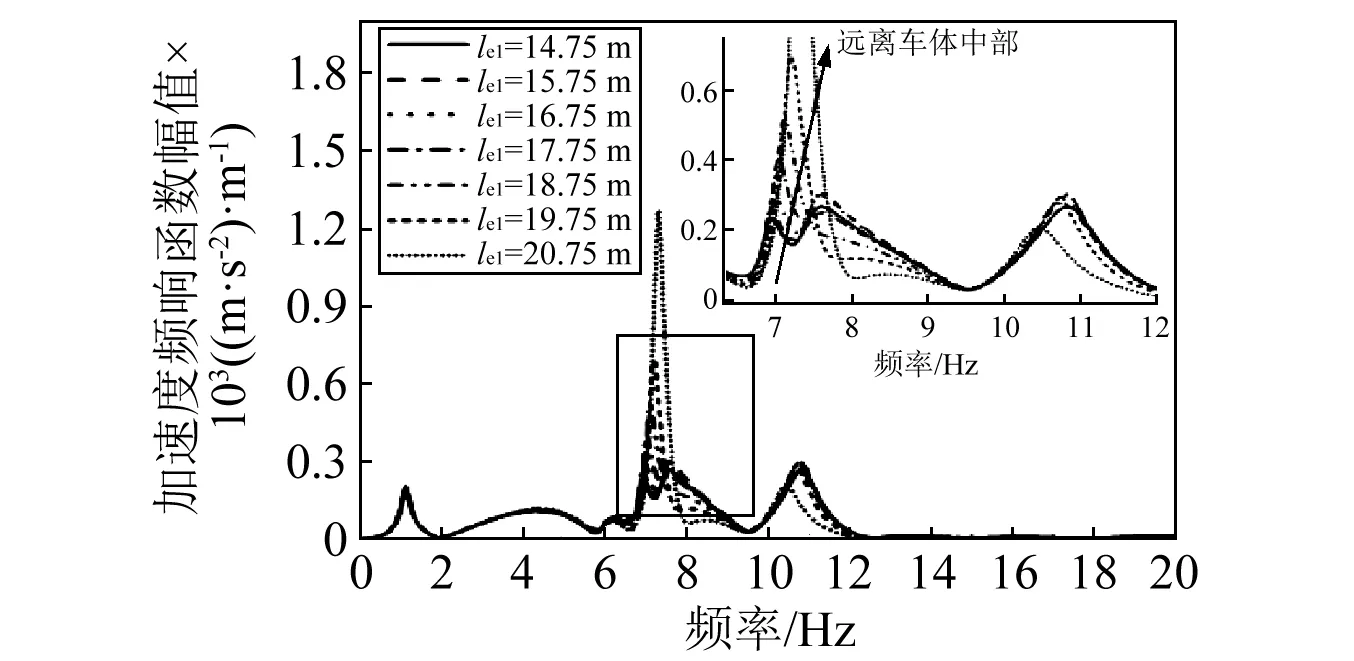
图11 框架连接位置对车体中部振动影响Fig.11 The influence of frame connecting position on center vehicle

表3为设备1、框架位置变化车体高阶垂弯频率分布，由表可知，车下设备位置分布不同，车体垂弯频率不同。表中垂弯频率最大为10.83 Hz，最小为10.43 Hz，车体高阶垂弯频率有0.4 Hz的变化。当设备1、框架均布置在车体中部时，垂弯频率最大(10.83 Hz)，且车体振动较小，这是因为设备布置在车体中部，使得车体的截面刚度在一定程度上有所上升，车体的高阶垂向弯曲频率会有所增大；而车体在高阶垂弯频率处振动与车下设备振动反相，故车体的弯曲振动得到了一定程度的抑制。

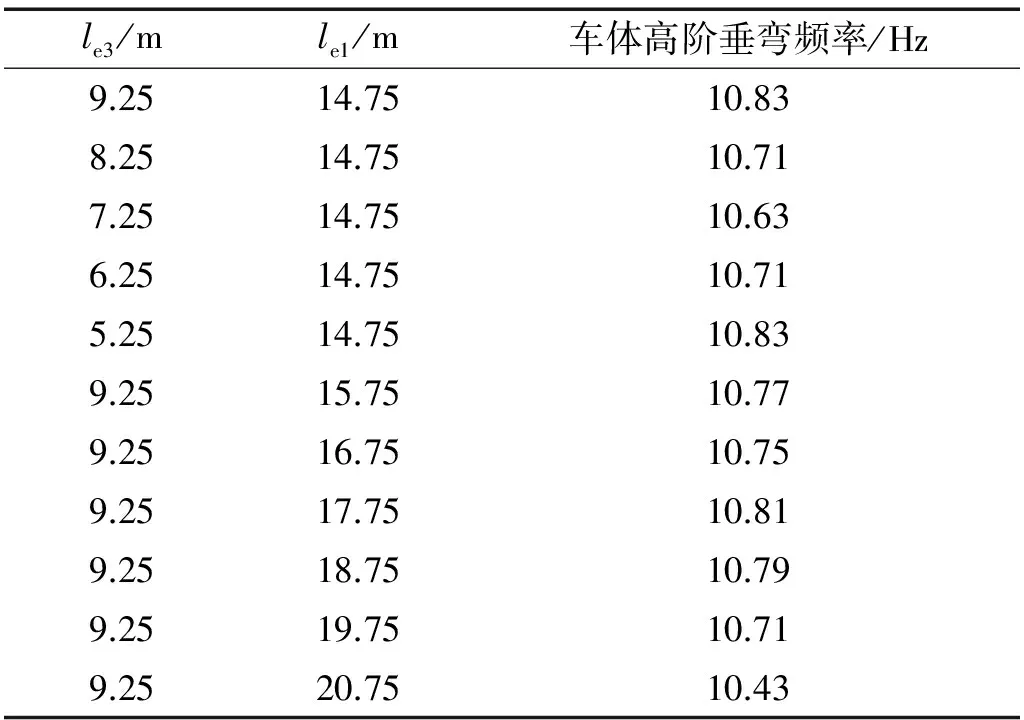
表3 设备1位置变化车体高阶垂弯频率分布

5 结 论

本文建立了多级多悬挂设备建立了车辆-设备刚柔耦合数学模型，研究了车体和设备的耦合振动特性以及相互影响关系，主要结论如下：

(1)速度作为几何滤波效应的影响因素，对研究车体-设备耦合振动系统响应特性有重要影响。

(2)设备1、框架、设备2吊挂刚度为1Kei(i=1,2,3)时，三阶垂向弯曲模态解耦程度较高，车体中部振动幅度较小，从车体振动控制角度来看，该吊挂刚度属于较优吊挂刚度。

(3)因为框架连接着设备2和车体，其模态容易发生耦合振动，导致设备2和框架在6～12 Hz内的模态解耦效果较差。当车体振动较小时框架和设备振动较大；当框架和设备振动较大时，车体振动就较小。

(4)随着设备1逐渐远离车体中部，车体在第2阶垂弯模态频率处的振动逐渐增大，同时车体前两阶垂弯频率带宽逐渐增大；当lel≤17.75 m时，框架系统的两阶模态不会发生耦合振动，随着框架远离车体中部，车体中部响应随之增大。无论是设备1还是框架远离车体中部，其自身振动都会逐渐增大。设备布置越靠近车体中部，车体的低阶垂弯模态更易解耦，能显著降低车体中部振动，同时能使车体高频垂弯频率最大提高0.4 Hz。

[ 1 ] 黄问盈,黄民.21世纪初铁道高速列车特色[J]. 铁道机车车辆,2009,29(2):23-30.

HUANG Wenying,HUANG Min.Distinct features of railway high speed train in early year of the 21th century[J].Railway Locomotive amp;Car, 2009,29(2):23-30.

[ 2 ] 宫岛,周劲松,孙文静,等.下吊设备对高速列车弹性车体垂向运行平稳性影响[J].中国工程机械学报,2011,9(4):404-409.

GONG Dao, ZHOU Jinsong, SUN Wenjing, et al. Impact of hanging equipments on vertical riding stability of elastic high-speed train bodies [J].Chinese Journal of Construction Mechinery, 2011,9(4):404-409.

[ 3 ] 罗光兵,曾京.车下设备的连接方式及悬挂参数匹配研究[J].现代制造工程,2013(5):1-6.

LUO Guangbing, ZENG Jing. Study on car body flexible vibration with considering under frame suspended equipment [J].Modern Manufacturing Engineering, 2013(5):1-6.

[ 4 ] 吴会超,邬平波,曾京,等. 车下设备对车体振动的影响[J]. 交通运输工程学报,2012,12(5):50-56.

WU Huichao, WU Pingbo, ZENG Jing, et al. Influence of equipment under car on car body vibration [J].Journal of Traffic and Transportation Engineering, 2012,12(5):50-56.

[ 5 ] 吴会超,邬平波,吴娜,等.车下设备悬挂参数与车体结构之间匹配关系研究[J]. 振动与冲击,2013,32(3):124-128.

WU Huichao, WU Pingbo, WU Na, et al. Matching relations between equipment suspension parameter and a car body structure[J].Journal of Vibration and Shock, 2013,32(3):124-128.

[ 6 ] 周劲松,孙文静,宫岛. 铁道车辆几何滤波现象及弹性车体共振分析[J]. 同济大学学报(自然科学版),2009,37(12):1653-1657.

ZHOU Jinsong, SUN Wenjing, GONG Dao. Analysis on geometric filtering phenomenon and flexible car body resonant vibration of railway vehicle [J].Journal of Tongji University (Natural Science), 2009, 37(12):1653-1657.

[ 7 ] DUMITRIU M.Influence of the vertical suspension on the vibration behavior in the railway vehicles [J].Annals of the University of Petrolane, Mechanical Engineering, 2011,13:35-50.

[ 8 ] DUMITRIU M.On the critical points of vertical vibration in a railway vehicle [J].Archive of Mechanical Engineering, 2014,61(4):609-625.

[ 9 ] ZHOU J,GOODALL R,REN L,et al.Influences of car body vertical flexibility on ride quality of passenger railway vehicles[J].Journal of Rail and Rapid Transit, 2009, 223(5)：461-471.

[10] GONG Dao, SUN Wenjing, ZHOU Jinsong, et al.Analysis on the vertical coupled vibration between bogies and metro car body[J].Procedia Engineering, 2011，16:825-831.

[11] DUMITRIU M.Evaluation of the comfort index in railway vehicles depending on the vertical suspension features[M].Tome: International Journal of Engineering,2013.

[12] GONG Dao, ZHOU Jinsong, SUN Wenjing.On the resonant vibration of a flexible railway car body and its suppression with a dynamic vibration absorber [J].Journal of Vibration and Control, 2012,19(5):649-657.

Theinfluenceofmultistageandsuspensionmulti-equipmentontheverticalvibrationofhigh-speedvehicles

HE Xiaolong, ZHANG Limin, LU Liantao, ZHOU Hui

(State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031，China)

In this article, a rigid-elastic coupling vehicle-equipment system has been established taking the high speed train with multistage and suspension multi-equipment as a research object. The acceleration frequency response characteristics above the car body center and bogie were obtained. Also, the vehicle-equipment coupling vibration characteristic and interactional relationship has been investigated with considering geometry filtering effect, the equipment connecting method (rigid, elastic), the connecting stiffness and the connecting position. The result shows that: the speed has an important influence on the vehicle vertical response; the connecting parameters mainly affect the vehicle 6-12 Hz; the frame and the car body more easily generate coupling vibration compared to the equipment 1 and 2; the middle car body vibration becomes quite tiny while the equipment and frame have the converse result when connecting stuffiness is 1Kei(i=1,2,3). The connecting position closer to the middle vehicle, the smaller the middle vehicle vibratio. The higher vertical bending frequency can reach 0.4 Hz.

multistage and multi-equipment; acceleration frequency response function; geometric filtering effect; elastic connecting parameter; mount position

国家自然科学基金(51675443)

2016-08-17 修改稿收到日期：2016-11-23

贺小龙 男，博士生，1989年生

张立民 男，博士，研究员，1961年生

U463.33

A

10.13465/j.cnki.jvs.2017.22.038