低矮建筑屋盖风雪流作用场地实测与数值模拟

赵 雷, 余志祥,2, 齐 欣, 赵世春

(1. 西南交通大学 土木工程学院， 成都 610031；2. 西南交通大学 高速铁路线路工程教育部重点实验室， 成都 610031)

低矮建筑屋盖风雪流作用场地实测与数值模拟

赵 雷1, 余志祥1,2, 齐 欣1, 赵世春1

(1. 西南交通大学 土木工程学院， 成都 610031；2. 西南交通大学 高速铁路线路工程教育部重点实验室， 成都 610031)

为了研究风雪流对低矮建筑屋盖的作用，制作了6组缩尺模型，在常遇雪天气候下，开展了屋盖积雪特性场地实测与模化分析，考虑了典型的阶梯型屋面以及平屋面、双坡屋面、女儿墙等因素的影响，提出了典型低矮建筑屋盖积雪荷载模化模型。研究表明：阶梯型屋面的积雪分布与已有的场地实测及风洞试验结果相似；平屋面雪荷载沿来流方向呈倒U型分布，可模化为均匀分布，但随着风速变化，积雪漂移使积雪形态可能向倒V型演化，建议考虑其线性非均匀分布对结构的不利影响；风速较低时，双坡屋面的积雪漂移量较少，对迎风侧屋盖更不利，国内外规范均侧重考虑了积雪漂移对背风侧的影响，建议考虑弱风条件下积雪漂移对迎风侧的不利影响；女儿墙的存在使屋面积雪量有较大的增加，屋盖前缘和后缘区域的漂移长度差异较大。结合风洞试验与场地实测，考虑雪粒子与风场的双向耦合、雪粒碰撞、黏结，探索性地对阶梯型屋面的积雪分布进行了二维数值模拟，论证了DEM-CFD风雪流模拟方法的可行性。

风雪流；低矮建筑；屋盖结构; 场地实测；数值模拟；规范

随着全球极端气候的频繁出现，因风雪流作用导致房屋结构垮塌的报道常见诸于媒体，既有事故调查表明：雪荷载过大、局部不均匀堆载及风雪耦合作用是导致灾害发生的主要原因[1]。特别是近年来被广泛使用的大跨度建筑钢结构，因其竖向刚度较弱、围护体系轻薄，对竖向荷载的非均匀分布较为敏感，加之风荷载是其主控作用之一，因此，风雪流灾害影响往往更为突出[2]。Majowiecki[3]也曾指出：风雪流产生的跃移及由此造成的建筑表面积雪的不均匀分布是大跨度结构设计必须考虑的问题之一。

目前，世界各国规范[4-7]基本上均将风荷载与雪荷载视作两种无相互作用的外部作用。屋面雪荷载常用基本雪压与一系列关联系数(如倾角系数、遮挡系数和热力系数等)的乘积确定，且差异较大，尤其针对雪荷载非均匀分布影响，亦主要按经验确定。而针对屋盖风荷载，既没考虑雪颗粒运动对风场的影响，也没考虑建筑气动外形和质量因积雪分布产生改变，进而影响气动特性这一重要问题。

针对风雪流，国内外学者采用理论分析、风洞试验、数值模拟及场地实测开展了大量研究。Tsuchiya等[8]对一阶梯形建筑缩尺模型进行了场地实测，模型高低两阶屋面的长×宽×高分别为5.4 m×1.8 m×1.8 m和5.4 m×4.5 m×0.9 m安装于离地面0.5 m的位置，测试了实测场地的温湿度、风速、风向以及低阶屋面的积雪分布形态，并与风洞试验结果进行比较，研究了绕流对屋面积雪特性的影响。Thiis[9]对一7.5 m×2.5 m×2.5 m的长方体模型以及两个相邻5.9 m，边长为2.5 m的立方体模型周边地面积雪模式进行了研究，揭示了风速与风致积雪漂移堆积情况的关系以及既存积雪对积雪沉积率的影响。O’Rourke等[10-12]采用解析方法计算了屋面雪荷载、风速数据及地面积雪分布等参数，统计计算获得N年重现期屋面最大雪荷载，并采用核桃壳粉粒模拟雪粒，在水槽中对屋面积雪分布进行试验研究，试验模型包括双坡屋面、平屋面和阶梯形屋面，分析了迎风侧屋面吹雪质量输运率。Cocca等[13]介绍了基于历史气象数据及数学模型估计屋面N年重现期雪荷载的方法。Tominaga等[14]基于两相流理论提出了改进吹雪沉积与侵蚀的计算方法，并对立方体建筑周边积雪进行数值模拟，得到与实测及风洞试验数据符合较好的结果。孙晓颖等[15]基于多相流模型，对几种典型大跨度屋盖的风雪流作用进行了数值模拟。王卫华等[16]采用石英砂模拟雪粒子，在边界层风洞中对典型阶梯形屋面及双坡屋面进行了积雪特性的试验研究。

鉴于风雪流作用的复杂性，场地实测已成为最直接、有效、可靠的研究方法。但既有的实测数据多针对风雪流输运特性以及建筑物周边积雪，而针对建筑屋面积雪的实测研究相对较少。故此，本文旨在采用场地实测的方式，兼顾考虑风雪流研究中典型的阶梯型屋面以及工程中常用的平屋面、双坡屋面、女儿墙等影响因素，对常遇雪天下的屋面积雪进行研究。同时，基于实测结果，与多国规范进行比较，分析两者差异，提出可供设计参考的建议。最后，基于DEM(Discrete Element Method)与CFD (Computational Fluid Dynamics)，考虑雪粒子的碰撞、黏结及其与风场的双向耦合，探索性地对阶梯型屋面积雪分布开展了二维数值模拟，结合风洞试验与实测数据论证了其有效性。

1 模型设计与实测

实测场地位于黑龙江省泰康县体育场(见图1)，该处地形开阔、平坦，适合进行场地实测，同时按GB 50009—2012规定，易判断其属于B类场地。因仅做机理性研究，故模型并无特定缩尺对象，采用胶合板、方木、合页及钢排钉，共制作了方便搬运、拆装的建筑模型共6组，其中典型阶梯型屋面及有、无女儿墙平屋面模型各1组，有、无女儿墙双坡屋面分别为2组及1组。除阶梯型屋面长度为3 000 mm外，其余模型长、宽、高均分别为1 500 mm、1 200 mm和1 200 mm，女儿墙高度为50 mm，模型特征及编号,如表1所示。模型摆放方位依据冬季该处气流主流方向以及场地的实际情况布置。实测模型及风速风向仪的布置方式，如图2所示。模型之间的横向间距为10 m，纵向间距为15 m，风速风向仪位于场地的正中心。

图1 实测场地Fig.1 Measured field

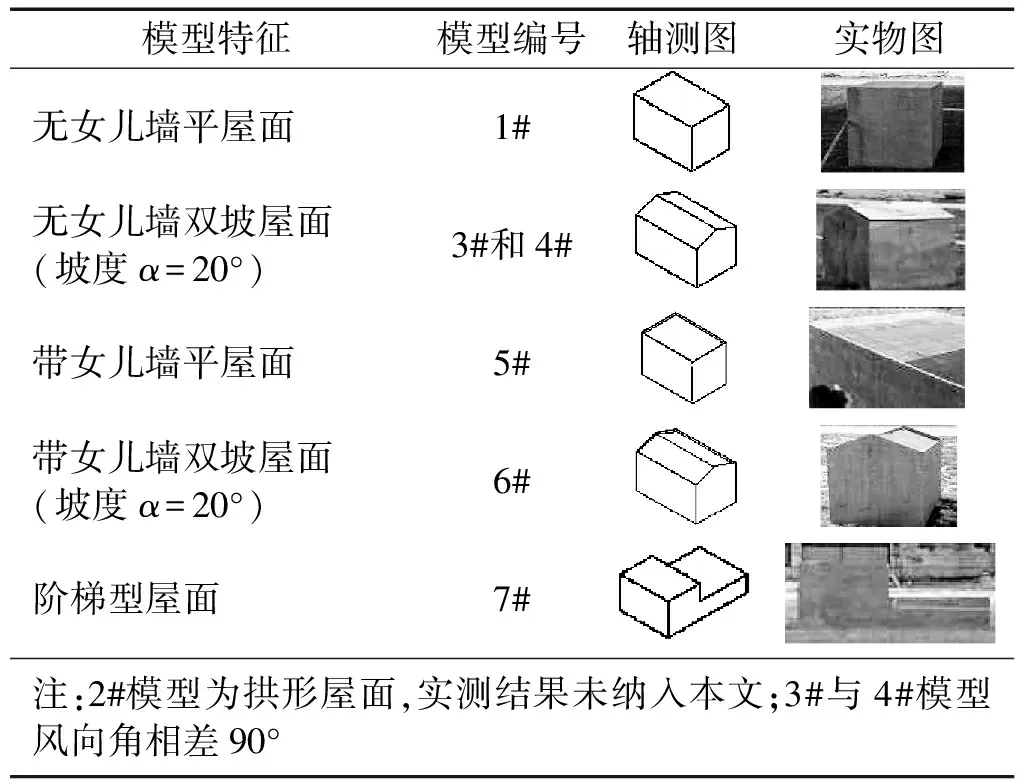
表1 模型特征及标号

(a)平面示意 (b)实物照片图2 模型布置方式Fig.2 Layout of models

实测内容包括降雪期间的风速风向、模型屋面的积雪深度及场地的平均积雪深度。风速风向采用YGY-FSXY1风速风向仪测量，采集时间间隔为10 min，传感器安置高度为2.5 m。积雪深度采用游标卡尺竖直插入进行测量，测点采用标线仪进行激光定位，测点纵横向间距为50 mm，沿屋面均匀分布，并在积雪深度预期变化梯度大的区域适当加密，通过Kriging方法对测点数据进行三维反演，获得屋面积雪分布特征。场地地面积雪深度的测点位于该体育场跑道，该跑道冬季用作滑冰赛道，降雪前即为平整光滑的冰面，利于地面积雪深度的准确测量，同时，采用多次随机采样取平均值的方式获得实测场地的地面积雪深度。

2015-02-22/02-23，当地降中到大雪，雪停后立即进行测量。按前述测量方式，随机选取8个测点测得地面积雪平均深度为42 mm。根据实测(见图3)，可知降雪期间风向以西南偏西为主，而且风速较小，实测风速v1约为1.77 m/s。结合当地实测空气密度ρ1与理想空气密度ρ0(12.5 kg/m3)对v1进行修正，其中ρ1依据实测场地海拔高度h按式(1)计算，修正后实测平均风速v2(式(2))为1.74 m/s。

ρ1=1.25e-0.000 1h

(1)

(2)

按指数律风速剖面[17]转化为10 m标准高度处的平均风速约为2.17 m/s。

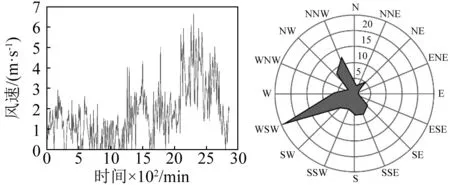
(a)风速时程曲线 (b)风向频率玫瑰图图3 气象资料Fig.3 Meteorological data

为了更直观地反映屋面积雪分布实测的结果，本文中定义屋面积雪分布系数cs

(3)

式中：hr为屋面实测点积雪深度；hg为地面实测积雪深度的平均值。

2 积雪分布特征

2.1 平屋面

图4为无女儿墙平屋面积雪后的实际形态，图5为屋面积雪分布系数的实测结果。据图分析易知：模型四周檐口处因受气流剥离和积雪滑落影响，侵蚀较为严重，顺流向积雪厚度的变化梯度较大，其中靠屋面前缘的顺流向侵蚀长度(屋面边缘积雪深度急剧变化区域的宽度)约25 mm，背风侧大致为迎风面的2倍，达到50 mm；屋面积雪沿流向整体呈倒“U”型分布，积雪分布系数为0.4～0.8，具有一定非均匀分布特征。沿顺流向中轴的积雪分布可按断面面积相等简化为线性分布，其中迎风侧积雪系数为0.5，背风侧为0.75。

(a) (b)图4 1#模型实际积雪形态Fig.4 1# model after snowfall

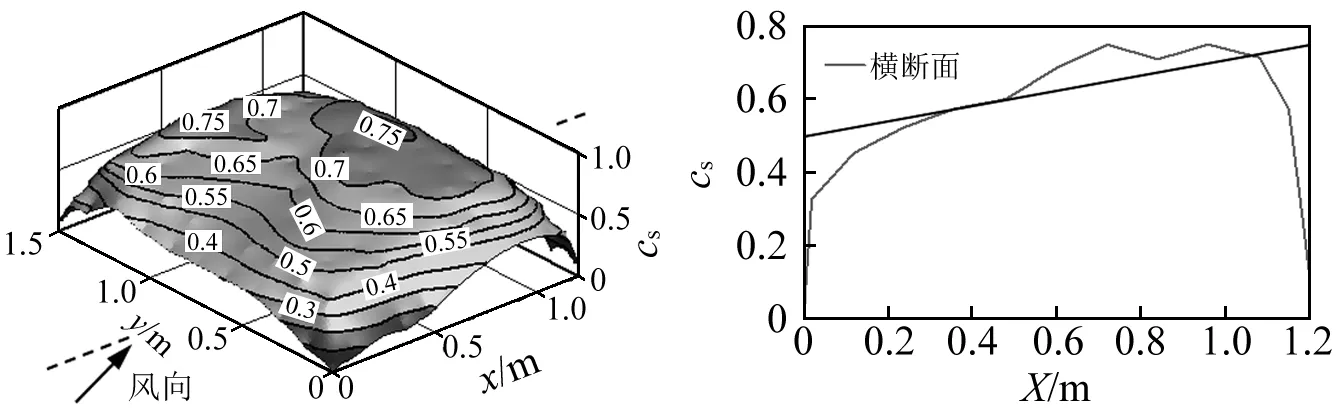
(a)屋面整体积雪分布 (b)横断面积雪分布图5 1#模型屋面积雪分布Fig.5 Snow distribution of 1# model

2.2 双坡屋面

图6为无女儿墙双坡屋面(3#及4#模型)积雪后的实际形态，两组模型的摆放角度正交(图2(a))；图7为模型屋面积雪分布系数的实测结果；图8为模型屋面积雪系数沿垂直于屋脊方向的中轴分布曲线。分析易知：2组模型在屋脊两侧均有积雪堆积，檐口位置亦有明显侵蚀，总体呈M形；迎风侧积雪分布系数均在顺流向长度x=0.25 m达到最大，其中3#、4#模型分别为0.8和0.75；背风侧较迎风侧的积雪系数均有增加，均在x=1.0 m处达到最大，其中3#模型最大值为0.9，4#模型为最大值为1.0；屋脊位置x=0.6 m处雪深系数均较小，其中3#模型为0.4，4#模型为0.3。2组模型横断面积雪分布系数的分布类似，4#模型虽然峰值较3#模型略大，但没有3#模型饱满；积雪分布系数按断面积等效可简化为阶梯型，其中迎风侧为0.65，背风侧为0.85。需特别指出的是，因来流风速较低，两组模型分布形态较为接近；同时，3#模型因其屋脊近似平行于来流风向，屋脊两侧积雪分布也更趋于对称。

(a)3#模型 (b)4#模型图6 3#和4#模型实际积雪形态Fig.6 3# and 4# models after snowfall

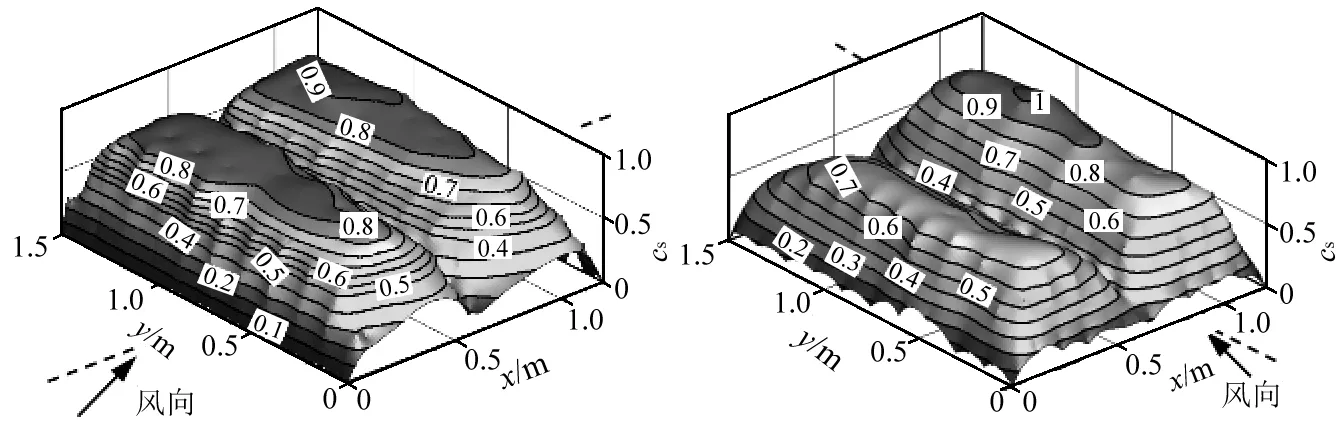
(a)3#模型 (b)4#模型图7 3#和4#模型屋面积雪分布Fig.7 Snow distribution of 3# and 4# models

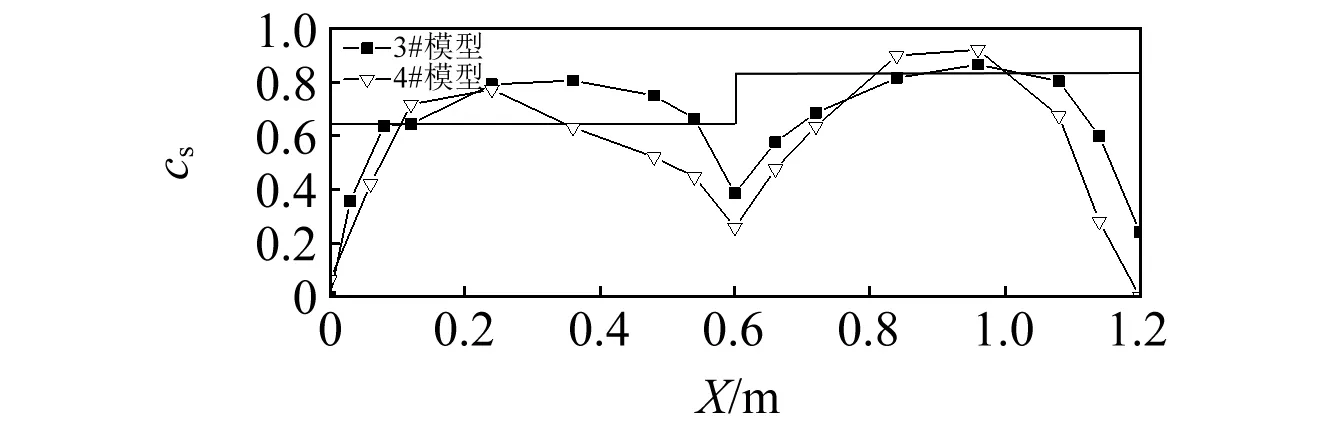
图8 3#和4#模型屋面横断面积雪分布Fig.8 Snow distribution on cross section

2.3 阶梯型屋面

图9为典型阶梯型屋面积雪后的实际形态，图10为低屋面积雪分布系数的实测结果。分析易知：cs从低屋面屋檐(x/H=0)处的0.2缓慢增加到x/H=2.1位置处达到最大，最大值为的1.4，随后快速下降至x/H=2.8位置处的0.3，最后在低屋面末端(x/H=3)处急剧增加至1.2。低屋面积雪在x/H=2.1～2.8位置处所受风力的掏蚀作用非常明显。

(a) (b)图9 7#模型实际积雪形态Fig.9 7# model after snowfall

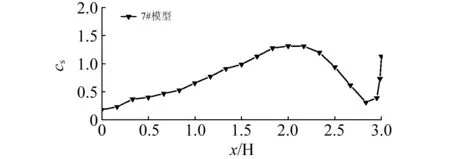
图10 7#模型低屋面积雪分布Fig.10 Snow distribution of 7# model

2.4 女儿墙对屋面积雪分布的影响

图11为有无女儿墙时沿模型中轴横断面的积雪系数实测结果，包含平屋面及双坡屋面两种模型，共计四组参数。研究发现：相同屋面形状时，女儿墙对积雪系数的分布模式影响不大，但女儿墙的存在削弱了相邻屋面的气流剥离作用，使屋檐位置处积雪分布系数明显增大(见图11(a))；其分布规律为：沿顺流向迎风侧的影响约10倍女儿墙高范围，背风侧靠近女儿墙附近的影响约2～4倍墙高范围，且双坡屋面影响更甚；现行规范中除ASCE规范规定女儿墙的影响范围与墙高和积雪深度相关外，中、加、欧规范均只规定为2倍墙高，远低于本文实测；同时，从积雪横断面积比较来看，女儿墙的存在使平均积雪系数增大约20%。

(a)平屋面 (b)双坡屋面图11 女儿墙对屋面积雪分布的影响Fig.11 Snow distribution influenced by parapets

3 实测结果与现行规范的比较

中国规范、ASCE规范、NBC规范及EU规范中雪荷载的计算公式分别为

Sk=μrS0

(4)

Ps=0.7CsCeCtIpg

(5)

S=Is[Ss(CbCwCsCa)+Sr]

(6)

S=μiCeCtsk

(7)

式中：Sk、ps、S均为屋面雪荷载；S0、pg、Ss、sk均为基本雪压；μr为屋面积雪分布系数；Cs为倾斜系数，反映屋面坡度的影响；Ce为遮挡系数，反映周围环境对建筑物的遮挡效应；Ct为热力系数，反映建筑物采暖情况的影响；I，Is为建筑物重要性系数；Cb为屋面雪荷载基本系数，除大跨度屋面有特殊规定外，一般情况下均取为0.8；Cw为风力系数，反映风对屋面积雪的影响；Ca、μi均为屋面形状系数；Sr为关联的雨水荷载，并且不大于Ss(CbCwCsCa)。此外，ASCE规范和NBC规范还将屋面分为光滑屋面和非光滑屋面。

为方便比较，可通过合理的参数设置，使得规范计算得到的雪荷载与本文式(3)所定义的屋面积雪分布系数cs具有相同的物理意义。参数设置如下：均按非光滑屋面考虑；ASCE规范的Ce、Ct及I，NBC规范的Is、Cw、Sr，EU规范的Ce、Ct均取为1.0，NBC规范中Cb取0.8；基本雪压为单位值。

3.1 平屋面

平屋面雪载分布实测值及相关规范计算值,如图12(a)所示。由图12(a)可知，本文实测结果与欧、美、加三国规范的计算值较为接近，而中国规范的计算值则偏安全。这一定程度也证明了本文实测结果的有效性。

图12(b)为平屋面的雪载形态，由图12(b)可知，4个国家的规范均只考虑了雪荷载的均匀分布。但根据风雪流的基本理论易判断，随着风速增大，平屋面不均匀堆积特征也会加大，屋盖积雪系数倒U型分布具有向到V型演化的趋势，随着跨中积雪增大，可能对大跨度屋盖的不利影响会加剧。因此，结合本文实测结果，建议平屋面雪荷载同时考虑均匀分布与线性非均匀分布(见图12(b))两种形态，本文实测积雪系数可供参考。

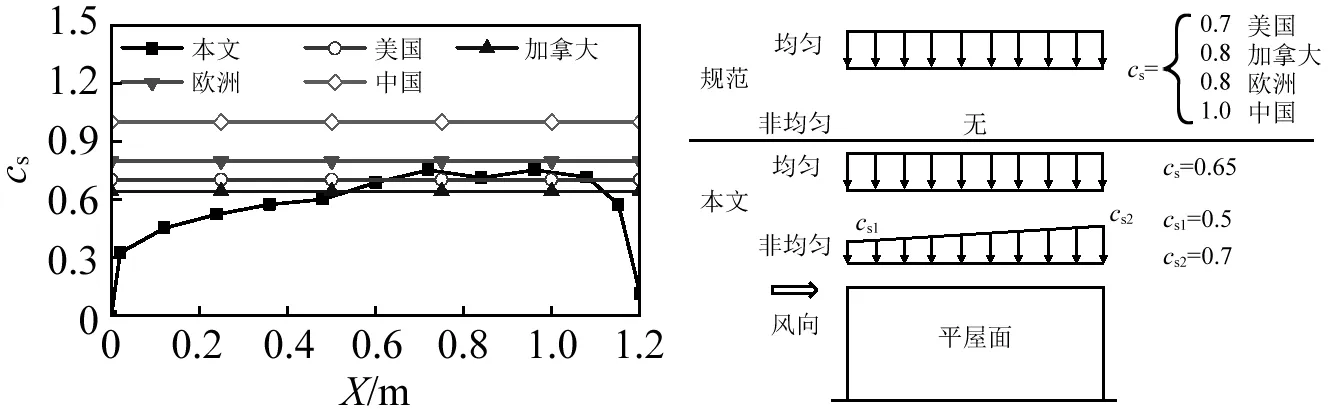
(a)分布系数 (b)分布形态 图12 平屋面雪荷载分布Fig.12 Snow load distribution on flat roof

3.2 双坡屋面

据图13(a)分析可知，针对双坡屋面，欧、美、加3个国家规范的均布积雪系数计算值与本文实测值更接近，中国规范计算值偏大。当考虑非均匀分布时(见图13(b))，在迎风侧，除中国规范值与本文实测值很接近外，其余3个国家的规范值明显偏低，背风侧本文实测值与欧洲及美国规范更为接近，中国及加拿大规范则有较大富余。4个国家的规范中双坡屋面的非均匀积雪分布状态均依据积雪的漂移量确定，如美国规范规定当屋盖跨不大于6.1 m时，迎风侧100%漂移，而当跨度大于6.1 m时，迎风侧则70%发生漂移，中国、加拿大和欧洲规范则分别按25%、100%和50%考虑，因此有较大差异。

(a)均匀分布 (b)非均匀分布图13 双坡屋面积雪分布系数Fig.13 Snow load distribution coefficient on pitched roof

4 风雪流模拟

基于本文阶梯型屋面积雪的部分实测数据，进一步对采用DEM-CFD方法进行风雪流数值模拟展开了探索性研究。和传统多相流方法相比，该方法可考虑雪粒子的碰撞、黏结，以及风与雪之间的双向耦合作用。

4.1 流域及边界条件

根据Tsuchiya实测模型(见图14(a))(H=0.9 m)构建了二维流场，计算域长31 m，高10 m，宽度方向为4层厚0.05 m的单元，网格划分采用分块结构性网格(见图14(b))，最小网格尺寸为0.01 m。

(a)实测模型 (b)计算网格图14 计算模型示意Fig.1 Diagram of calculation model

入口为速度边界(velocity-inlet)，出口位置沿流向的压力梯度为0，流域顶部及两侧面均采用对称边界条件(symmetry)，等价于自由滑移壁面，建筑物表面及地面均采用无滑移的壁面条件(wall)。兼顾计算量并参考相关文献的研究结果，选用Realizablek-ε湍流模型与加强壁面函数的组合可取得不错的CFD模拟结果。

入口处风速剖面采用指数函数[18]，标准参考高度处的平均风速取为24 m/s；地面粗糙度指数α，根据Davenport的建议，取0.16。湍流强度Iu、湍动能k和湍流耗散率ε的的取值参考文献[19-20]建议，本文不再赘述。上述入口参量采用UDF (User-Defined Functions)编程与Fluent作接口实现。

4.2 雪颗粒相关参数

采用球形模型对雪粒子进行模拟，忽略雪颗粒的升华、融化等物理现象。采用Hertz-Mindlin (No Slip)模型[21-24]考虑雪颗粒之间及雪颗粒与壁面之间的碰撞，基于Linear Cohesion模型[25]通过添加法向凝聚力的方式修正Hertz-Mindlin (No Slip)模型来考虑雪颗粒之间的黏性，相关参数设置如表2所示。

表2 接触模型参数

模型壁面采用混凝土材料，雪粒子及混凝土相关参数，如表3所示。

表3 材料参数

4.3 耦合求解方法

采用Eulerian耦合方法进行求解，该方法通过体积分数α对连续性方程进行修正来考虑雪颗粒与风场相互作用。忽略雪颗粒与流场之间热交换，仅考虑质量守恒及动量守恒。流体的连续性方程为

(8)

式中：下标F为流体；下标P为粒子；α为体积分数；ρ为密度；v为速度；m为质量。

每个单元中粒子质量的改变率为

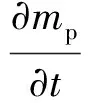
(9)

式中,τ为CFD的计算时间步。

动量守恒方程为

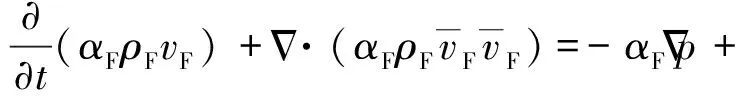
(10)

式中：下标F为流体；τF为黏性应力张量；p为压力；Pp为从颗粒处获得的动量；g为重力加速度。

耦合计算前采用“4.2”节参数，在阶梯型屋面的低阶屋面上铺设0.1 m厚的雪颗粒，如图14所示。其中DEM的计算时间步长为5×10-5s，为瑞利时间步长的50%；网格尺寸为0.01 m，即颗粒半径的2倍。CFD计算时间步长设为0.01 s，总模拟计算时间为2.5 s。曳力模型采用Freesteam Equation方式，升力采用Saffman模型。

4.4 计算结果

图15(a)和图15(b)为不同时刻粒子的迹线图，图15(c)和图15(d)为模型周围流线图以及粒子的分布形态，易知：流场的分离、再附、驻涡等绕流特征明显；低阶屋檐处剥离较为严重，粒子受其影响发生悬移运动，中后段粒子以跃移及蠕移为主，部分跃移粒子在撞击到壁面后下落到低屋面尾端，而尾端受驻涡影响较大，粒子分布出现明显的堆积及掏蚀。仿真时长达到0.6 s后，屋面积雪分布形态基本稳定，表现为低屋面中前端的粒子受到驻涡影响向迎风侧发生蠕移，到屋檐处时受到剥离的影响随即发生悬移。

(a)t=0.2 s (b)t=0.4 s (c)t=0.6 s (d)t=0.8 s图15 迹线、流线及粒子分布形态 Fig.15 Path lines,streamlines and particle distribution

图16为阶梯型屋面在无积雪时流场特性的风洞试验以及数值模拟结果。可知，有无积雪时流场在高低屋面的前缘均会出现较强的分离流动，在建筑物的后方均会出现较大的回流漩涡，但由于积雪与雪颗粒悬移的存在，使得低屋面上方的回流漩涡出现明显削弱。

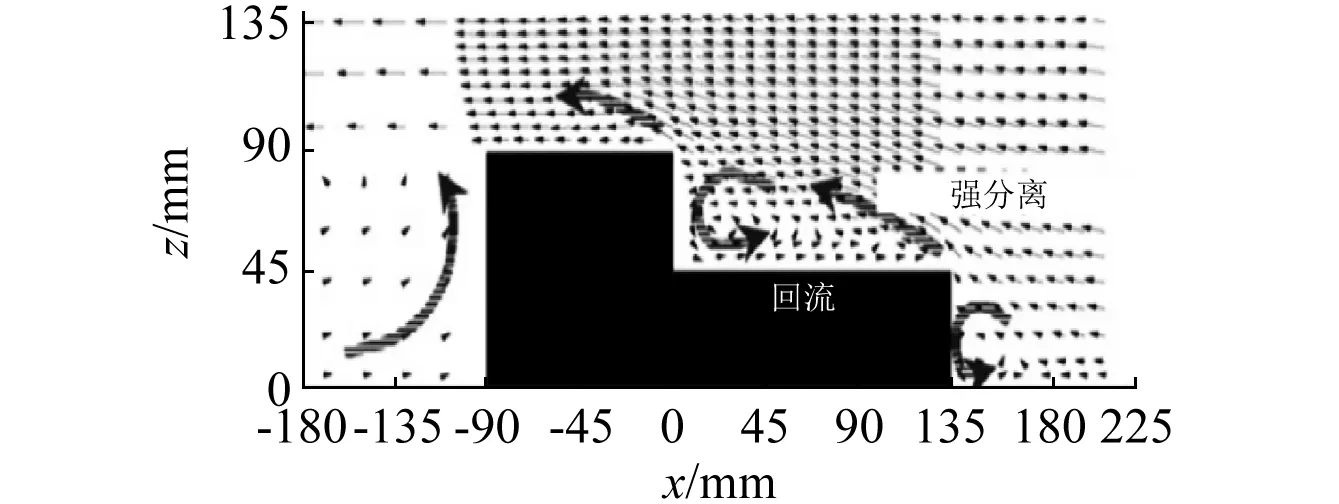
(a)风洞试验

(b)数值仿真[26]图16 无积雪分布时流场特性Fig.16 Flow field characteristics without snow

图17给出了t=0.8 s时低屋面cs的分布曲线，计算时hg取为初始铺设的积雪深度。图中同时给出了前文的场地实测结果以及Tsuchiya的3次场地实测结果和王卫华等在XNJD-3风洞实验室的试验结果。由图17可知,模拟值与1#试验值较为接近，本文实测值与3#试验值较为一致，模拟结果与5组试验值的分布态势总体一致，但在靠近最大积雪深度位置的梯度略有差异，其原因和风吹雪作用时间、下雪量、风向等都有关系。

区别主要体现在：场地实测时cs的最大值为1.0～1.6，位于x/H=2.2～2.4，而仿真计算结果的最大值则为1.2，位于在x/H=2.5处；在x/H=2.3～2.7区域内，场地实测值快速下降至0.1～0.3，但计算结果直至x/H=2.9处才达到最小，为0.7，其分布特征与风洞试验更为接近；在低屋面末端(x/H=3.0)处，均有一定的堆积出现，实测结果为0.7～1.9，风洞试验值为0.98，计算结果则为1.1。

分析其差异的原因主要在于：①实测时其主风向并非完全正风向，而是与屋面有一定夹角；②场地实测时，Tsuchiya的实测模型特征高度H=0.9 m，并安置于离地面0.5 m位置处，本文作者实测模型的特征高度H=0.6 m，并安置于地面，而计算时模型安置于地面且特征高度H=0.9 m；③计算时所采用的k-ε湍流模型本身具有局限性，其不足主要体现在绕流时，迎风侧檐口前侧气流剥离位置的湍动能容易过高估计，同时伴随着后侧湍动分离不足；④风雪流风洞试验在雪粒子合理等代上争议较大。

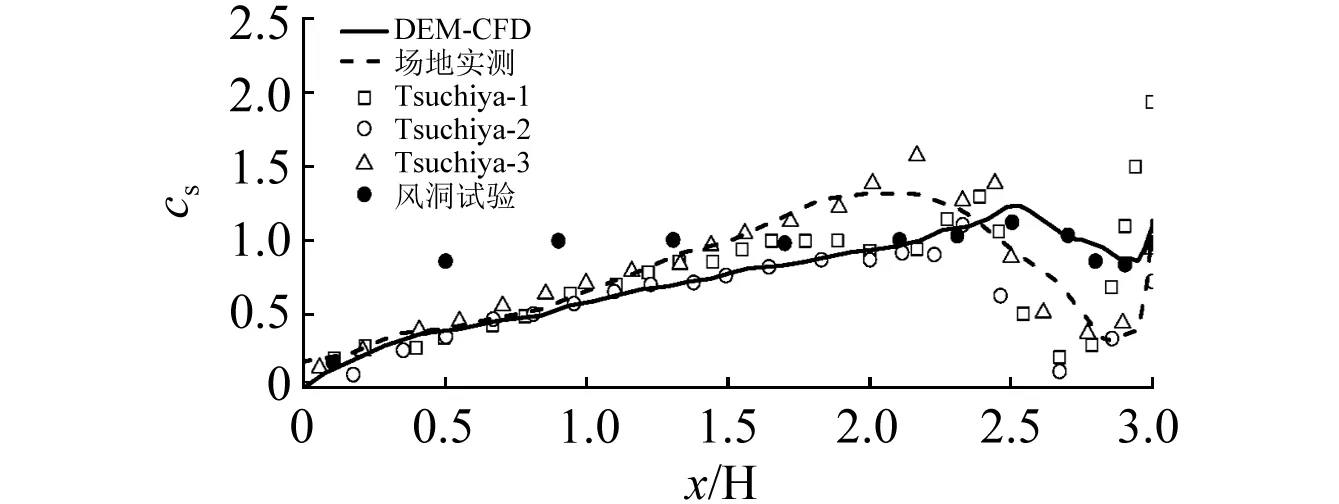
图17 低屋面积雪分布Fig.17 Snow distribution on the low roof

5 结 论

综上所述，可得：

(1) 平屋面积雪沿来流方向呈倒U型分布，随着风速增大，积雪漂移使积雪形态可能向倒V型演化，建议考虑其线性非均匀分布对结构的不利影响。

(2)女儿墙的存在使屋面积雪加剧，且屋盖前缘和后缘区域的漂移长度差异较大。

(3)采用DEM-CFD进行风雪流数值模拟是可行的，该方法可考虑雪粒子运动特征及雪粒子对流场的影响，2D模拟结果与实测试验值吻合较好，这位采用计算机模拟进一步预测积雪形态提供了途径。

[ 1 ] 王元清,胡宗文,石永久,等. 门式刚架轻型房屋钢结构雪灾事故分析与反思[J]. 土木工程学报, 2009, 42(3): 65-70.

WANG Yuanqing, HU Zongwen,SHI Yongjiu,et al. Analysis and reflection on snow disaster accidents of steel structures of light-weight buildings with portal frames[J].China Civil Engineering Journal, 2009, 42(3): 65-70.

[ 2 ] 蓝声宁,钟新谷. 湘潭轻型钢结构厂房雪灾受损分析与思考[J]. 土木工程学报, 2009, 42(3): 71-75.

LAN Shengning, ZHONG Xingu. Damage diagnoses and lessons learnt from the failure of lightsteel structures by heavy snow in Xiangtan[J]. China Civil Engineering Journal, 2009, 42(3): 71-75.

[ 3 ] MAJOWIECKI M. Snow and wind experimental analysisin the design of long-span sub-horizontal structures[J]. Journal of Wind Engineering amp; Industrial Aerodynamics, 1998, (74/75/76): 795-807.

[ 4 ] 建筑结构荷载规范: GB 50009-2012[S]. 北京: 中国建筑工业出版社, 2012.

[ 5 ] Minimum design loads for buildings and other structures: ASCE 7-10[S]. New York: ASCE, 2010.

[ 6 ] National Building Code of Canada: NRC-IRC[S]. Ottawa: NRCC, 2005.

[ 7 ] Eurocode 1-actions on structure-Part 1-3: general actions-snow loads: BSI. BS EN 1991-1-3: 2003[S]. London: BSI, 2003.

[ 8 ] TSUCHIYA M, TOMABECHI T, HONGOA T, et al. Wind effects on snowdrift on stepped flat roofs[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(12): 1881-1892.

[ 9 ] THIIS T K. Large scale studies of development of snowdrifts around buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91(6): 829-839.

[10] O’ROURKE M, DEGAETANO A. Analytical evaluation of drift loads [J]. Proceedings of the 2004 Structures Congress-Building on the Past: Securing the Future. Blandford： ASCE, 2004: 1-11.

[11] O’ROURKE M, DEGAETANO A, TOKARCZYK J D. Snow drifting transport rates from water flume simulation[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2004,92(4): 1245-1264.

[12] O’ROURKE M, DEGAETANO A, TOKARCZYK J D. Analytical simulation of snow drift loading [J]. Journal of Structural Engineering, 2005, 131(4): 660-667.

[13] COCCA J, O’ROURKE M. Mathematical simulation of 50-year snow drift loads [J]. Structures Congress, 2008: 1-9.

[14] TOMINAGA Y, OKAZE T, MOCHIDA A. CFD modeling of snowdrift around a building: an overview of models and evaluation of a new approach [J]. Building and Environment, 2011, 46(4): 899-910.

[15] 孙晓颖,洪财滨,武岳. 典型形式大跨度屋盖风雪漂移的数值模拟[J]. 振动与冲击, 2014, 33(18): 36-42.

SUN Xiaoying, HONG Caibin, WU Yue. Numerical simulation of snow drifting on typical long-span roofs [J]. Journal of Vibration and Shock, 2014, 33(18): 36-42.

[16] 王卫华, 廖海黎, 李明水. 风致屋面积雪分布风洞试验研究[J]. 建筑结构学报, 2014, 35(5): 135-141.

WANG Weihua, LIAO Haili, LI Mingshui. Wind tunnel test on wind-induced roof snow distribution [J]. Journal of Building Structures, 2014, 35(5): 135-141.

[17] 殷惠君. 膜结构风荷载的数值模拟研究[D]. 上海: 同济大学, 2006.

[18] DAVENPORT A.G. The relationship of wind structure to wind loading [C]//Proc. of the Symposium on Wind Effect on Building and Structure. London: [s.n.], 1965: 54-102.

[19] 余志祥, 闫雁军. 近壁区网格△y对TTU建筑风场湍流计算的影响[J]. 土木建筑与环境工程, 2012, 34(6): 46-51.

YU Zhixiang, YAN Yanjun. Influence on turbulent flow calculation of wind flow around TTU building by grid size △yin near-wall region[J]. Journal of Civil, Architectural amp; Environmental Engineering, 2012, 34(6): 46-51.

[20] Recommendations for loads on buildings: AIJ-RLB-2004[S]. Tokyo: Architectural Institute of Japan, 2004.

[21] HERTZ H. On the contact of elastic solids[J]. J. Reine Angew. Math, 1881, 92(110): 156-171.

[22] MINDLIN R D. Compliance of elastic bodies in contact[J]. Journal of Applied Mechanics, 1949, 16: 259-268.

[23] TSUJI Y, TANAKA T, ISHIDA T. Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe [J]. Powder Technology, 1992, 71(3): 239-250.

[24] CUNDALL P A, STRACK O D L. A discrete numerical model for granular assemblies [J]. Geotechnique, 1979, 29(1): 47-65.

[25] DEM Solutions. EDEM 2.2 User Guide [M/OL]. 2009.

[26] 王卫华. 风致屋面积雪分布特性风洞试验与数值模拟研究[D].成都：西南交通大学,2014.

Fieldmeasurementsandnumericalsimulationofsnowdriftonlow-risebuildings

ZHAO Lei1, YU Zhixiang1,2, QI Xin1, ZHAO Shichun1

(1. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China；2. Key Laboratory of High-speed Railway Engineering, Ministry of Education， Southwest Jiaotong University, Chengdu 610031, China)

Field measurements and numerical simulations were adapted to research snowdrifts on low-rise buildings. Typical roofs including stepped flat roof, flat roof and pitched roof were considered. Snow load models on typical roofs were put forward. The results show thatcson stepped flat roof is similar to the existing results,cson flat roof increases along the wind direction, presenting an inverted u-shaped distribution, and can be simplified as an uniform distribution. With the changing of wind speed,cstrends to the evolution of inverted “V”. The adverse effect due to the linear inhomogeneous distribution should be considered. On the pitched roof, the amount of snowdrift is less on the condition of weak wind weather, the adverse effect on the windward side is suggested to be considered. Snow load on the plat roof and the pitched roof both increase due to the existence of parapets, and the drift length on the windward side is much higher than that on the Leeward side. At last, a coupled CFD and DEM method was used to simulate snowdrift on typical stepped flat roof, considering collision and bonding of snow, and the simulation results had a good consistency with the existing field measurement.

snowdrift; low-rise buildings; roof structure; field measurement; numerical simulation; norms

国家自然科学基金项目(51378428)；西南交通大学青年科技创新项目(SWJTU12CX069)

2016-04-27 修改稿收到日期： 2016-09-09

赵雷 男，博士生，1990年生

余志祥 男，博士，副教授 ，1976年生

TU312.1;TU317.1

A

10.13465/j.cnki.jvs.2017.22.035