基于SVD优化LMD的电梯导靴振动信号故障特征提取

陶 然， 许有才， 邓方华， 郭 澍， 李新仕， 苟 敏， 李 琨， 王 华

(1.昆明理工大学 质量发展研究院，昆明 600500； 2. 昆明理工大学 信息工程与自动化学院，昆明 600500；3.云南省特种设备安全检测研究院，昆明 650228)

基于SVD优化LMD的电梯导靴振动信号故障特征提取

陶 然1,3， 许有才2,3， 邓方华2,3， 郭 澍3， 李新仕3， 苟 敏2， 李 琨2， 王 华1

(1.昆明理工大学 质量发展研究院，昆明 600500； 2. 昆明理工大学 信息工程与自动化学院，昆明 600500；3.云南省特种设备安全检测研究院，昆明 650228)

针对局部均值分解(Local Mean Decomposition, LMD)方法提取电梯导靴振动信号的故障特征分量时存在的模态混淆现象，本文提出了一种基于奇异值分解(Singular Value Decomposition, SVD)优化局部均值分解(Local Mean Decomposition, LMD)的电梯导靴振动信号故障特征提取方法。该方法以奇异值贡献率原则构造原始信号的Hankel矩阵，采用SVD对Hankel矩阵进行分解；将曲率谱原则与奇异值贡献率原则相结合对奇异值进行选择，将包含主要故障信息的奇异值进行逆重构，得到剔除噪声信号与光滑信号的突变信号；并利用LMD方法对突变信号进行故障特征提取，得到能够突出原始信号振动特征的故障特征分量。实例结果表明该方法有效改善了LMD的模态混淆现象，更准确地提取了振动信号的故障特征分量，为电梯导靴的故障诊断提供了一条有效的途径。

电梯导靴；奇异值分解；局部均值分解；模态混淆；特征提取

电梯是特种设备的主要组成部分，近年来其安全事故频发，其安全状态引发了社会的广泛关注。导靴是在电梯导轨与轿厢之间滑动的导向装置，其主要作用是将轿厢固定在导轨上做上下运动。导靴作为垂直电梯的关键部件，其一旦发生故障轻则导致轿厢运行颠簸、曳引绳磨损，重则导致轿厢变形、损坏导轨造成安全事故。

当导靴发生故障时，其振动信号会表现出明显的非线性、非平稳性。对于非线性、非平稳振动信号，需要采用合适的时频分析方法提取故障特征分量[1]。常用的时频分析方法有小波变换、经验模态分解(Empirical Model Decomposition, EMD)、局部均值分解(Local Mean Decomposition，LMD)等[2-3]。但是小波变换缺乏自适应性，EMD方法虽然具有自适应性，但是存在过包络、欠包络、端点效应和无物理意义的负频率等局限性[4]。相比EMD而言，LMD虽然具有端点效应不明显、虚假分量少，不会出现负频率的优点，但其分解得到的乘积函数(Product Function, PF)分量中仍然存在模态混淆现象。模态混淆现象包括两种情况：①一个PF分量中包含差异极大的两种及两种以上特征时间尺度信号；②相近的特征时间尺度分布在不同的PF分量中。本文针对的是模态混淆现象的第二种情况，因为最大程度地提取故障产生的特征时间尺度分量是故障识别的关键步骤。

为了更好地展现故障产生的特征时间尺度分量，本文对提取了信号的瞬时Teager能量谱。瞬时Teager能量谱能够很好地突出信号的瞬时幅值变化，可以很好地展现LMD方法存在的模态混淆现象。

SVD(Singular Value Decomposition)具有良好的数值稳健性与自适应性，通过对奇异值分析能够有效识别噪声分量和故障特征分量。近年来，该方法在信号处理[5]、数据挖掘[6]及故障诊断[7-9]等领域得到了广泛应用。本文将SVD的降噪滤波优势与LMD的故障特征提取优势相结合应用于电梯导靴的故障诊断。通过对比试验表明，该方法有效提取了电梯导靴振动信号的故障特征分量，有效改善了LMD的模态混淆现象，为电梯导靴的故障诊断提供了一个有效的参考方法。

1 SVD与LMD的基本理论

电梯在正常运行期间，导靴的振动信号受工作环境的影响较多，例如，曳引机、排风机、随行电缆、补偿链等部件。因此，采集的振动信号具有强噪声背景的特点，如果仅直接采用LMD进行故障特征分量提取，很难得到理想的故障特征时间尺度分量。因此，采用SVD对信号进行预处理有利于改善LMD的模态混淆现象，提高导靴故障诊断准确率。

1.1 SVD的基本理论

在信号处理领域，SVD是一种经典的正交变换方法。该方法对任意一个行或列线性相关的矩阵，通过对其左、右分别相乘一个正交矩阵进行变换，将原矩阵转化为一个奇异值矩阵(对角矩阵)，且得到的奇异值个数反映原矩阵中独立行(列)矢量的个数，而其大小表征了信号的内在属性。该算法具有良好的稳定性和不变性，可用来对信号进行降噪滤波、特征提取和弱信号分离等。根据SVD理论，对于一个矩阵A∈Rm×n，必存在正交矩阵U，V使得

(1)

式中，对角阵S=[diag[σ1,σ2,…,σq]0]或者其转置。SVD具体内容参见文献[10]。

1.2 构建吸引子轨迹矩阵

实验采集到的导靴振动信号是行向量，而SVD理论处理的对象是二维矩阵。因此，需要采用适当的方法将导靴振动信号构造成合适的m×n维矩阵A。

构造矩阵A的形式不同，则SVD处理的效果就不一样。目前，构造矩阵A的常用方法有两种：①通过对信号的连续截断来构造矩阵；②构造吸引子轨迹矩阵，及Hankel矩阵。这两种方法的共同特点是：都可以将信号表示为一系列分量信号的线性叠加。而方法①矩阵得到的分量信号是彼此正交的，具有较好的频率分辨率；方法②矩阵得到的分量信号虽然不具有正交性，却有很好的去噪效果，可以获得包含故障特征的高信噪比信号[11]。

为了获得包含故障特征的高信噪比信号，本文采用方法②将采集到的一维振动信号X=[x1,x2,…,xN]构造成m×n维Hankel矩阵A，采用奇异值贡献率方法自适应确定Hankel矩阵的维数m、n。

式中，1lt;nlt;N。令m=N-n+1，则A∈Rm×n，A∈Rm×n。

1.3 奇异值贡献率

由SVD理论可知，其得到的分量所包含的信息量直接由相应奇异值σk的大小决定，σk越大则表示该奇异值对应分量的信息量越多。因此，可以定义奇异值贡献率ηk来综合衡量对应分量的信息量[12]

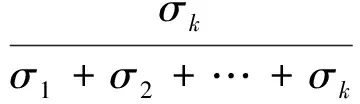
(2)

根据奇异值贡献率的大小自适应确定Hankel矩阵的维数m、n的原则：若取一系列m值，随着m增大，从某一贡献率ηk开始后贡献率都趋于零，则表明第k个分量之后的其他分量并没有多大意义，此时可以确定矩阵行数m=k，而对于列数，第一种矩阵为n=int(N/m)，第二种矩阵为n=N-m+1。

1.4 奇异值曲率谱

对于离散奇异值曲线的曲率，首先将所有奇异值按照从大到小的顺序构造一个序列，记为S={σ1,σ2,…,σq}；各点奇异值的曲率为

(3)

曲率谱的最大峰值坐标位置，即奇异值曲线上最大曲率Ck处的坐标位置。k可以作为有效奇异值和噪声奇异值的分界点，如果奇异值曲线在k点是凸出的，则有效奇异值为前k个；如果奇异值曲线在k点是凹进的，则有效奇异值为前k-1个[13]。因此，式(1)可以表示为：A=D+W，D为光滑信号与突变信号对应的轨迹矩阵，W为噪声对应的轨迹矩阵[14]。为了将故障突变信号对应的轨迹矩阵从D中分离出来，本文再次采用奇异值贡献率对D中的奇异值进行自适应选择。由于奇异值贡献率ηk越大，则该奇异值包含的故障突变信息越多。因此，可以从D中选择若干个ηk较大的奇异值经SVD逆运算得到故障突变信号对应的轨迹矩阵。因此式(1)可以表示为A=Q+D+W,Q为突变信号对应的轨迹矩阵。根据Hankel矩阵的特点，将Q的第一行与最后一列组成行(列)向量，就可以得到剔除光滑信号和噪声后的突变信号。

1.5 局部均值分解

LMD方法是科研工作者Jonathan S.Smith于2005年，在EMD方法的研究基础上提出的。LMD方法是一种基于局部时间尺度的振动特征提取方法，即能从原始振动信号中提取包含局部振动特征的PF分量。与EMD相比，LMD是一种自适应性更强、端点效应不明显的时频分析方法，但由于信号具有间歇性且受噪声的干扰，其仍然不能很好地从原始信号中提取突出原始信号局部振动特征的特征时间尺度分量，即模态混淆现象[15]。因此，文献[16]提出了一种总体局部均值分解方法，该方法虽然使模态混淆现象得到了一定了的改善，但是该方法加入了大量白噪声并且残留在提取到的PF分量中。因此该方法的分解效果存在较大的局限性。为了实现电梯导靴故障的准确诊断，本文提出了一种基于SVD优化LMD的故障特征提取方法。该方法通过使用SVD对信号进行预处理，不仅保留了LMD时频分析的优势，而且有效改善了LMD的模态混淆现象。

LMD的实质是从原始振动信号中分离出纯调频信号和包络信号，将纯调频信号和包络信号相乘便可以得到具有物理意义的PF分量，迭代处理至所有的PF分量分离出来。对于任意信号x(t)，其处理结果如式(4)，具体分解步骤参见文献[3]。

(4)

式中，u(t)为残余分量。

1.6 瞬时Teager能量谱

传统意义上的信号能量是幅值的平方，代表势能或动能。其虽然能够表征信号的瞬时幅值振动特征，但是对于冲击幅值较小，则该振动模态很容易被其它模态淹没[17]。

Teager-Kaiser能量算子(Teager-Kaiser Energy Operator, TKEO)是由Kaiser提出的一种非线性算子。该算子由信号瞬时幅值及其微分通过非线性组合成信号的总能量。与传统信号能量相比，该算子能更有效地提取信号的瞬时特征，并具有良好的时间分辨率，近年来被学者广泛应用于求取信号的瞬时振动特征。

离散信号x(n)的TKEO定义为

ψd[x(n)]=x2(n)-x(n-1)x(n+1)

由上式可知，计算任意离散时间信号的TKEO，只要该信号具有三个样本点即可计算任意点处的瞬时能量。因此，TKEO对信号的瞬时变化具有良好的时间分辨率，能够高精度地检测信号中的瞬态振动特征。

2 基于SVD优化LMD的故障特征提取

基于以上论述，本文提出的基于SVD优化LMD的电梯导靴振动信号故障特征提取方法，采用SVD从背景噪声和光滑信号中分离出含有故障突变信息分量；然后采用LMD从故障突变信号中提取微弱的电梯导靴故障特征分量。

该方法具体步骤如下：

步骤1 对一维原始振动信号x(t)构造m×n维Hankel矩阵A，初始令m=2，对A进行SVD得到奇异值矩阵S1，求奇异值贡献率Q1=[η1,η2,…,ηm-1]。

步骤2 令m=m+1，求得Qm-1，若Qk～Qm-1中始终有某个ηk小于某一较小值(本文取1.67%)，则循环结束，确定m=k及相应的n；否则继续进行步骤2循环，直到满足循环结束条件。

步骤3 对m×n维Hankel矩阵A进行SVD，得到奇异值矩阵Sm-1；采用“1.4”节中的奇异值曲率谱方法与奇异值贡献率原则自适应剔除噪声奇异值、光滑信号奇异值(奇异值置为零)保留突变信号有效奇异值；然后对突变信号奇异值矩阵采用SVD逆运算方法进行重构，得到突变信号x′(t)。

步骤4 对x′(t)进行LMD，得到突出原始信号振动特征的分量PFi。

3 实验研究

为了验证本文提出方法的有效性，采用上述原理和方法分别对电梯轿厢的上导靴故障信号、下导靴故障信号进行分析。本文采用的数据来源于云南省特种设备安全检测研究院。

实验采用B22型电梯导靴如图1所示。其具体参数如表1所示。在不影响导靴正常使用性能的情况下，用磨砂分别在上、下导靴侧面制作间隙为2.1 mm，轿厢为空载运行，采样频率为100 Hz。该电梯的额定载重量为800 kg，额定运行速度为1.0 m/s。为了能够清楚的阐述两种方法对比的效果，本文所用数据是电梯在检修速度运行时采集得到的。

滑动导靴的振动信号由安装在轿厢地面的三维陀螺仪加速度传感器进行检测，采用动态卡尔曼滤波算法。当导靴两侧出现磨损时，轿厢在与导靴两侧垂直方向的振动信号会产生冲击特性。

图1 B22型电梯导靴Fig.1 B22 type elevator guide shoe

表1 导靴参数

4 数据分析

本文采集轿厢导靴正常运行时的振动信号，如图2所示。轿厢下导靴故障振动信号如图3所示。对比图2和图3可知，导靴在正常运行情况运行时，振动信号比较平稳。当电梯下导靴发生故障时，其时域波形及瞬时Teager能量谱在4 ～5 s表现出了冲击特征，如何对该故障特征进行有效提取是故障诊断的第一步，也是最关键的一步。(由于篇幅限制，本文仅选取一组轿厢下导靴故障振动信号数据进行具体分析)。

为了验证本文提出方法的有效性，本文将分别采用SVD优化LMD方法与LMD方法对轿厢下导靴故障特征进行提取。

采用“1.3”节所述方法对轿厢下导靴故障信号构造m×n维Hankel矩阵，得到的奇异值序列k的贡献ηk率，如图4所示。由图4可知，当m≥8时，ηk(k≥9)逐渐趋向于零，并且lt;1.67%。因此，本文选取m=8构造Hankel矩阵。

图2 正常状态振动信号Fig.2 Normal vibration signal

图3 下导靴故障振动信号Fig.3 The down guide boots fault vibration signal

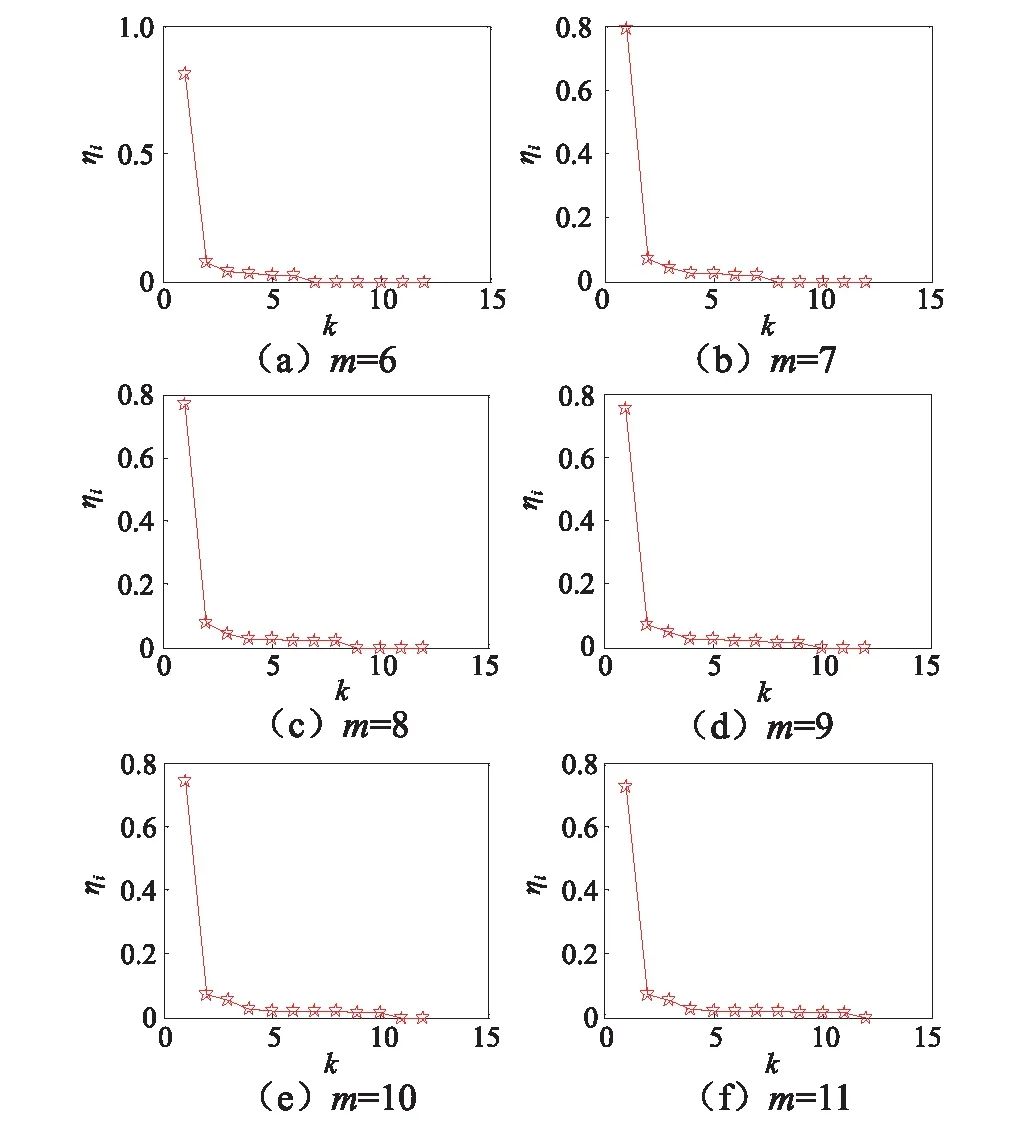
图4 奇异值贡献率Fig.4 Singular value contribution

为了从原始故障信号中将噪声与光滑信号剔除，得到突变信号，本文采用“1.4”节所述的奇异值曲率谱方法对奇异值进行筛选，得到的奇异值曲率谱和奇异值序列谱,如图5所示。

由图5可知，奇异值曲率谱峰值出现在第4个奇异值，根据奇异值曲率谱准则，第4个及其后的奇异值为背景噪声；结合图4(c)可知，第2个和第3个奇异值的贡献率与第1个奇异值贡献率相差甚大。因此，根据奇异值贡献率原则，第2个和第3个奇异值含有故障特征信息几乎为零，为光滑信号对应的奇异值，第1个奇异值为包含主要故障特征信息的奇异值，取第1个奇异值进行信号重构。

图5 奇异值曲率谱和奇异值序列谱Fig.5 Singular value curvature spectrum and singular value sequence spectrum

对第1个奇异值重构信号进行LMD，得到的PFi分量中，含有原始信号振动特征最多的分量是PF1，其次是PF2,PF3,…,PFn。因此，本文主要对PF1进行处理。PF1的时域波形图如图6(a)所示。其瞬时Teager能量谱如图6(b)所示。从瞬时Teager能量谱可以发现，从导靴发生故障时产生的波峰及其衰减的过程得到了很好复原，SVD优化LMD方法有效提取到了故障信号中的故障特征分量。

图6 SVD优化LMD方法PF1波形图Fig.6 The PF1 waveform figure of SVD optimizing LMD

采用LMD方法得到的PF1时域波形图，如图7(a)所示。其瞬时Teager能量谱如图7(b)所示。由图7可知，LMD方法虽然提取到了故障信号中的故障特征分量，但是从瞬时Teager能量谱可以发现，该方法只提取到发生故障时产生的波峰，故障分量的衰减过程几乎没有提取到。因此，可以得到LMD方法只提取到部分故障特征分量，还有部分故障特征分量仍然残留在残余信号中。即，使故障振动模态分解到多个信号中，存在模态混淆现象。

图7 LMD方法PF1波形图Fig.7 The PF1 waveform figure of LMD

通过图6和图7的分析可知，SVD优化LMD方法有效改善了LMD方法在提取故障特征分量时产生的模态混淆现象，使电梯导靴的故障特征分量得到了完整的提取，有利于后期电梯导靴的故障识别。同时，瞬时Teager能量谱很好地还原了导靴发生故障的全过程。

当电梯上导靴发生故障时，其时域波形如图8(a)所示。瞬时Teager能量谱如图8(b)所示。从图8可知，其振动信号第3 s前后表现出了冲击特征。采用SVD优化LMD方法对其进行特征提取，得到的PF1时域波形图如图9(a)所示。其瞬时Teager能量谱如图9(b)所示。从图9可知，该方法有效提取了上导靴从发生故障时产生的波峰及其衰减的过程。

图8 上导靴故障振动信号Fig.8 The up guide boots fault vibration signal

图9 SVD优化LMD方法PF1波形图Fig.9 The PF1 waveform figure of SVD optimizing LMD

5 结 论

LMD可以自适应的将一个振动信号分解为一系列的PF分量。本文提出的基于SVD优化LMD方法，使其模态混淆现象得到了改善，而且通过电梯导靴故障信号验证了其特性。通过对应用实例的分析结果表明：

(1)SVD及SVD逆重构能够在强噪声背景下有效降低噪声信号对故障特征信号的影响，从而得到高信噪比信号。

(2)基于SVD优化LMD的振动信号故障特征提取方法有效改善了LMD存在的模态混淆现象。

(3)本文提出的基于SVD优化LMD的电梯导靴振动信号故障特征提取方法能够有效提取电梯导靴振动信号中的故障特征分量，为电梯导靴的故障诊断提供了一条有效的途径。

[ 1 ] 张进，冯志鹏，褚福磊. 滚动轴承故障特征的时间-小波能量谱提取方法[J]. 机械工程学报，2011,47(17)： 44-49.

ZHANG Jin, FENG Zhipeng, CHU Fulei. Rolling bearing fault feature with time-the wavelet energy spectrum extraction method[J]. Journal of Mechanical Engineering, 2011, 47(17): 44-49.

[ 2 ] 杨江天，周培钰. 经验模态分解和Laplace小波在机车柴油机齿轮系故障诊断中的应用[J]. 机械工程学报,2011,47(7): 109-115.

YANG Jiangtian, ZHOU Peiyu. Empirical mode decomposition and Laplace wavelet in the application of locomotive diesel engine gear fault diagnosis[J]. Journal of Mechanical Engineering, 2011, 47(7): 109-115.

[ 3 ] 何田,林意洲,郝普刚,等.局部均值分解在齿轮故障诊断中的应用研究[J]. 振动与冲击,2011,30(6): 196-201.

HE Tian, LIN Yizhou, HAO Pugang, et al. Local mean decomposition in the application of gear fault diagnosis research[J]. Journal of Vibration and Shock, 2011, 30(6): 196-201.

[ 4 ] SMITH J S. The local mean decomposition and its application to EEG perception data[J]. Journal of the Royal Society Interface, 2005, 2(5): 443.

[ 5 ] KIM Y A, PHALAK R. Atrust prediction framework in rating-based experience sharing social networks without a web of trust[J]. Information Sciences,2012,191(1): 128-145.

[ 6 ] FOULIRAS P. A novel reputation-based model for e-commerce[J]. Operational Research, 2014, 13(1): 113-138.

[ 7 ] 甘早斌,曾灿,李开,等.电子商务下的信任网络构造与优化[J].计算机学报，2012,35(1): 27-37.

GAN Zaobin, ZENG Can, LI Kai, et al. Construction and optimization of trust network in e-commerce environment[J]. Chinese Journal of Computers, 2012, 35(1): 27-37.

[ 8 ] 张少中,方朝曦,陈军敢,等.基于社会网络的电子商务信任社区聚类模型[J].浙江大学学报(工学版),2013,47(4): 654-661.

ZHANG Shaozhong, FANG Chaoxi, CHEN Jungan, et al. Community clustering model for e-commerce trust based on social network[J]. Journal of Zhejiang University (Engineering Science), 2013,47(4): 654-661.

[ 9 ] YAHYAOUI H, ZHIOUA S. Bootstrapping trust of web services through behavior observation[J]. Knowledge and Information Systems,2013, 37(2): 389-416.

[10] 赵学智,叶邦彦,林颖. 奇异值分解对轴承振动信号中调幅特征信息的提取[J].北京理工大学学报,2011,31(5): 572-577.

ZHAO Xuezhi, YE Bangyan, LIN Ying. Amplitude modulation feature extraction of bearing vibration signal using singular value decomposition[J]. Transactions of Beijing Institude of Technology,2011,31(5): 572-577.

[11] 李葵,范玉刚,吴建德.基于二次奇异值分解与VPMCD的故障诊断方法[J].计算机工程,2015,41(4): 181-186.

LI Kui, FAN Yugang, WU Jiande. Fault diagnosis method based on quadratic singular value decomposition and VPMCD[J]. Computer Engineering,2015,41(4): 181-186.

[12] 赵学智,叶邦彦,陈统坚. 矩阵构造对奇异值分解信号处理效果的影响[J]. 华南理工大学学报(自然科学版),2008,36(9): 86-93.

ZHAO Xuezhi, YE Bangyan, CHEN Tongjian. Influence of matrix creation way on signal processing[J]. Journal of South China University (Natural Science),2008,36(9): 86-93.

[13] 赵学智，叶邦彦，陈统坚.基于奇异值曲率普的有效奇异值选择[J].华南理工大学学报(自然科学版),2010,38(6): 11-18.

ZHAO Xuezhi, YE Bangyan, CHEN Tongjian. Selection of effective singular values based on curvature spectrum of singular values[J]. Journal of South China University(Natural Science),2010, 38(6): 11-18.

[14] 李葵,范玉刚,吴建德.基于SVD和TKEO的轴承振动信号特征提取[J].计算机工程与应用,2014,50(17): 195-199.

LI Kui, FAN Yugang, WU Jiande. Feature extraction of bearing vibration signal based on SVD and TKEO[J]. Computer Engineering and Applications, 2014,50(17): 195-199.

[15] 程军圣，张亢，杨宇，等. 局部均值分解与经验模式分解的对比研究[J]. 振动与冲击,2009,28(5): 13-16.

CHENG Junsheng, ZHANG Kang, YANG Yu, et al. The comparative study of local mean decomposition and empirical model decomposition[J]. Journal of Vibration and Shock, 2009, 28(5): 13-16.

[16] 程军圣,张亢,杨宇. 基于噪声辅助分析的总体局部均值分解方法[J]. 机械工程学报, 2011,47(3): 55-62.

CHENG Junsheng, ZHANG Kang, YANG Yu. Ensemble local mean decomposition method based on noise-assisted analysis[J]. Journal of Mechanical Engineering, 2011, 47(3): 55-62.

[17] 王天金,冯志鹏,郝如江,等.基于Teager能量算子的滚动轴承故障诊断研究[J].振动与冲击,2012,31(2): 1-5.

WANG Tianjin, FENG Zhipeng, HAO Rujiang, et al. Fault diagnosis of rolling element bearing bsed on Teager energy operator[J]. Journal of Vibration and Shock,2012,31(2): 1-5.

FeatureextractionofanelevatorguideshoevibrationsignalbasedonSVDoptimizingLMD

TAORan1,3,XUYoucai2,3,DENGFanghua2,3,GUOShu3,LIXinshi3,GOUMin2,LIKun2,WANGHua1

(1.KunmingUniversityofScienceandTechnology,QualityDecelopmentInstitute,Kunming600500,China;2.KunmingUniversityofScienceandTechnology,FacultyofInformationEngineeringandAutomation，Kunming600500，China；3.SpecialEquipmentSafetyInspectionInstituteinYunnanProvince,Kunming650228,China)

Aimed at the phenomenon of mode mixing when the LMD is used to extract the fault information from an elevator guide shoe, a feature extraction method based on singular value decomposition (SVD) optimizing local mean decomposition (LMD) was proposed. First, the Hankel matrix of the original signal was constructed with singular value contribution principle. It used SVD to decompose the Hankel matrix. Then, in order to obtain the useful singular value containing the main fault information, the method selected singular values with the principle of curvature spectrum and the principle of singular value contribution. A mutation signal was reconstructed. Finally, the fault feature component which represented the original signal vibration characteristics could be extracted from the mutation signal by the LMD method. The method was applied to diagnose the elevator up guide shoe fault and the elevator down guide boots fault. Application examples show that the proposed method is effective to solve the problem of mode mixing and can extract fault characteristic components from the elevator guide shoe vibration signal more accurately.

elevator guide shoe;singular value decomposition(SVD); local mean decomposition(LMD);mode mixing;feature extraction

国家质检总局科技计划项目资助(2013QK104)；云南省质量技术监督局科技计划项目资助(2013YNZJKJ02)

2016-11-22 修改稿收到日期： 2017-02-06

陶然 男，博士生，1966年生

王华 男，博士，教授，博士生导师，1965年生

TH277

A

10.13465/j.cnki.jvs.2017.22.026