基于CEEMDAN与SVD的泄流结构振动信号降噪方法

张建伟， 侯 鸽， 暴振磊， 张翌娜， 马 颖

(1.华北水利水电大学 水利学院，郑州 450045；2.黄河水利职业技术学院 土木与交通工程学院，河南 开封 475004)

基于CEEMDAN与SVD的泄流结构振动信号降噪方法

张建伟1， 侯 鸽1， 暴振磊1， 张翌娜2， 马 颖1

(1.华北水利水电大学 水利学院，郑州 450045；2.黄河水利职业技术学院 土木与交通工程学院，河南 开封 475004)

针对泄流结构振动信号非平稳性和特征信息被强噪声淹没的实际问题，提出一种基于具有自适应噪声的完整集成经验模态分解(CEEMDAN)和奇异值分解(SVD)联合的信号降噪方法。对一维泄流振动信号时程进行CEEMDAN分解，将信号分解为一系列固有模态函数分量(IMF)，运用频谱分析方法筛选包含主要振动信息的IMF分量，滤除低频水流噪声，实现信号的初次滤波；利用排列熵理论确定含噪声较多的IMF分量，采用奇异值分解技术提取奇异值信息，运用奇异熵增量定阶理论滤除IMF分量中的高频噪声，实现信号的二次滤波；将包含结构振动信息的IMF分量重构，得到泄流结构的工作特征信息。结合拉西瓦模型振动实测数据，运用该方法进行计算分析，滤除高频和低频噪声，提取结构振动特征信息；结果表明该方法在泄流结构特征信息提取方面具有优越性，可为泄流结构在线监测和安全运行提供依据。

泄流结构；集成经验模态分解；排列熵；奇异值分解；特性信息

随着水利工程高水头、大流量、超流速泄水建筑物的兴建以及结构材料轻型化趋势的发展，水流与结构耦合作用诱发泄流结构振动问题日益突出，严重影响泄流结构安全运行，通过泄流振动信息判断其运行健康状况及振动危害程度成为水利工程研究热点之一[1]。泄流结构振动信号在输送和获取的过程中，容易受到环境激励的高频白噪声和低频水流噪声的干扰，通常表现为低信噪比、非平稳随机信号。结构振动特征信息完全淹没在强噪声中，难以精确识别其模态信息，从而影响结构健康状况及振动危害评价的精度。因此，需采取有效的信号分析方法对实测数据降噪处理，以获取结构振动信号的优势特征信息。

近年来，由于计算机运算速度的日益更新以及试验技术的进步，信号分析理论和技术方法取得了很大发展。经验模态分解 (Empirical Mode Decomposition，EMD)是由Huang等[2]提出的一种适用于处理非线性非平稳信号的时频分析方法，该方法依据信号自身尺度特征自适应分解成一系列从高频到低频的具有不同物理意义的固态模量(Intrinsic Mode Function，IMF)，具有较高的时频分辨率，已应用于多个领域信号研究中。贾瑞生等[3]针对微震信号具有高噪声、突变快、随机性强等特点，提出一种基于经验模态分解及独立成分分析的微震信号降噪方法；李琳等[4]提出一种适用于转子振动信号的小波分析和EMD相结合的去噪方法。EMD方法无需提前设定基函数，克服了小波分析等其它信号处理方法依赖主观经验的缺点，但由于其自身计算理论的缺陷，分解过程中容易出现模态混叠现象，影响分解效果。集合经验模态分解[5](Ensemble Empirical Mode Decomposition，EEMD)是对EMD的改进算法，该算法在原始信号中添加相应的白噪声来消除EMD分解中的模态混叠现象，并通过多次实验来抑制和抵消分解结果中噪声产生的影响，陈仁祥等[6]运用该算法进行了机械轴承振动信号的自适应降噪研究。EEMD算法在一定程度上解决了模态混叠问题，但是在有限次试验的集成平均后，其重构信号中仍然含有残余噪声，虽然可以通过增加集成次数来降低重构误差，但是其工作量十分庞大。因此，在EEMD的基础上，具有自适应白噪声的完整集成经验模态分解方法(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise，CEEMDAN)被提出，该算法通过在分解的每一阶段添加自适应的白噪声，计算唯一的余量信号获取各个模态分量，其分解过程是完整的。相比于EEMD算法，无论集成次数的多少，其重构误差几乎为零，解决了EEMD分解效率低的问题[7]。

基于上述研究，针对泄流振动信号淹没在高频白噪声和低频水流噪声的特点，本文提出一种基于CEEMDAN与奇异值分解联合的信号降噪方法。首先，泄流结构振动信号非平稳非线性的特性提供了运用CEEMDAN算法的可能性，利用CEEMDAN将泄流振动信号分解为一系列从高频到低频的IMF分量；其次，考虑到排列熵算法能够定量评估振动信号含有的随机噪声，还具有计算速度快、算法简单、抗干扰能力强等优点[8]，可利用排列熵确定需要进一步降噪的IMF分量，并利用奇异值分解对其进行降噪处理，滤除其高频随机噪声，得到准确物理意义的IMF分量；最后，重构信号得到反映结构动力特性的信号，实现强噪声背景下泄流结构工作特性有效信息的提取，为下一步结构健康诊断工作提供基础。

1 基本原理

1.1 CEEMDAN算法

EMD算法是将复杂的原始信号分解为一系列具有不同幅值的IMF分量和残余分量之和，将IMF分量按照瞬时频率由高到低的顺序分离出来。其实质就是对非线性、非平稳信号进行线性化、平稳化处理的过程，将复杂信号分解为单分量信号，从而获得更有实际物理意义的瞬时频率。EMD算法对信号具有一定的自适应性，但其模态混叠现象严重，影响信号分解的质量。

EEMD方法是在原始信号x(t)中多次添加不同的白噪声，分别对其进行EMD分解，对多次EMD分解的各IMF分量进行平均而得到最终的IMF分量，该方法能够一定程度上改善EMD算法的模态混叠现象。EEMD算法试图通过多次集成平均来抵消白噪声对分解结果的影响，但并未完全消除；其重构误差的大小对集成次数具有很大的依赖性，虽然可以通过增加集成次数来减少重构误差，但很大程度上又增加了计算耗时，严重影响计算效率。

相对于EEMD算法，CEEMDAN算法是在EMD分解的每个阶段添加有限次的自适应白噪声，即使在集成次数较少的情况下，其重构误差几乎为零，重构后的信号与原信号几乎完全相同。因此，CEEMDAN算法可以解决EMD算法中存在的模态混叠现象，同时克服了EEMD算法的不完整性以及依靠增大集成次数来降低重构误差而导致的计算效率低的缺陷。

CEEMDAN算法的具体实现步骤如下：

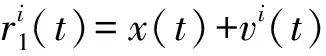
1.2 排列熵

排列熵(Permutation Entropy，PE)是由Bandt等最新提出的一种动力学分析方法，该方法能够精确检测出复杂系统的动力学突变，有效衡量一维时间序列的复杂度，特别适用于非线性信号的处理[9]。

假定长度为N的一维时间序列x(i)，其中i=1,2,3,…,N，以嵌入维数为m、延迟时间为τ对序列里每个元素进行相空间重构，得到的矩阵如下所示

(1)

式中,K为矩阵的行数，即重构分量的数目。将每一行的重构分量按照元素的数值大小进行升序排列，然后提取每个元素在排序前所在列的索引组成一个符号序列，对于m维相空间映射下的矩阵可能出现m！种符号序列，若第k种符号序列出现的概率记为Pk，则该时间序列x(i)的排列熵可表示为

(2)

对上述计算得到的HP(m)进行归一化处理，可得HP=HP(m)/ln(m！)。HP的取值在[0 1]，其大小反映了时间序列的随机性和复杂程度，其值越大，时间序列越复杂，表明该时间序列处于随机状态。反之亦然。

1.3 奇异值分解理论

奇异值分解(Singular Value Decomposition，SVD)作为一种经典的正交化分解降噪方法，对信号中的高频随机噪声具有很强滤除能力。SVD降噪本质在于信号经奇异值分解得到的矩阵奇异值是唯一的，同时奇异值具有稳定性、比例不变形等性质，使得奇异值作为一种有效描述信号内在属性的代数特征应用于信号处理中[10]。SVD降噪是将噪声对应的奇异值置零，将有用信号对应的奇异值保留，再利用奇异值分解的逆运算得到重构信号。

鉴于作者在文献[11-12]中对SVD理论已经进行了详细的研究，其理论部分不再赘述。

2 CEEMDAN-SVD联合降噪

针对含低频水流噪声和高频白噪声的低信噪比泄流信号，结合CEEMDAN和SVD的降噪特点，进行CEEMDAN-SVD联合滤波降噪。首先，利用CEEMDAN将泄流振动信号分解为一系列从高频到低频的IMF分量，运用频谱分析方法筛选包含主要结构振动信息的IMF分量，滤除低频水流噪声；其次，利用排列熵确定需进一步降噪的IMF分量，并利用奇异值分解对其进行降噪处理，滤除其高频随机噪声，保留其有效信息，实现信号的二次滤波；最后，运用频谱分析方法重构信号，最终得到反映结构振动特性的信号。CEEMDAN-SVD联合滤波降噪流程图如图1所示。

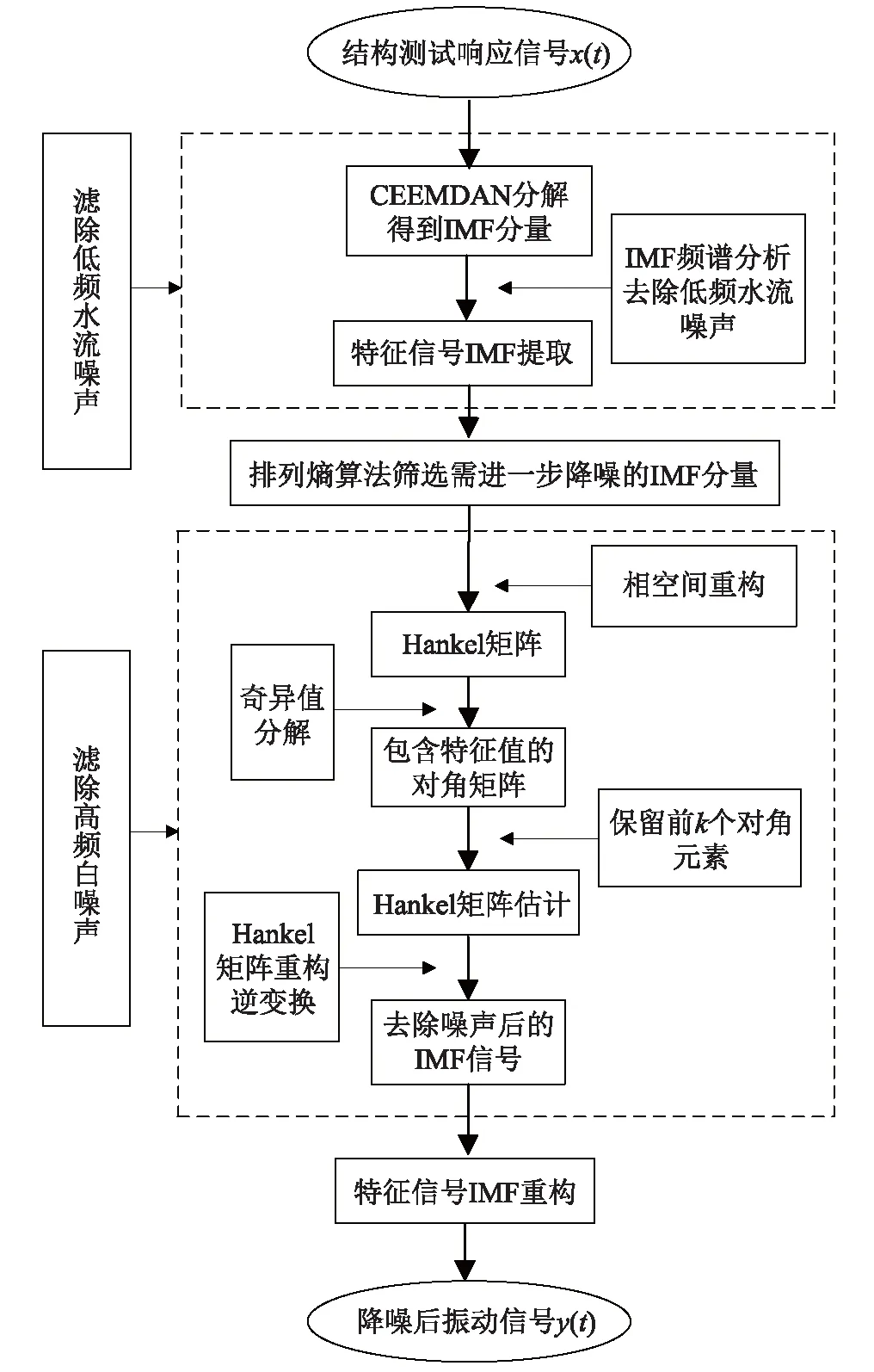
图1 CEEMDAN-SVD联合滤波方法流程图Fig.1 The flowchart of CEEMDAN-SVD method

3 工程实例

以拉西瓦拱坝为研究对象，采用加重橡胶建立比例尺为1∶100的水弹性模型，如图2所示。为反映拱坝振动情况，在坝顶设置11个动位移响应测点，在测点布置DP型地震式低频振动传感器，测点布置如图3所示。考虑到拱坝振动以径向为主，垂直向和切向振动相对较小，本文仅对径向振动(R方向)进行研究，振动测试系统采用DASP智能数据采集和信号分析系统，测试工况为表深孔联合泄洪，采样时间40 s，采样频率100 Hz。

应用本文方法对实测数据进行工作特性信息提取，限于篇幅，仅叙述坝顶振动响应最大点0#测点的处理过程，原始信号时程线和功率谱密度曲线，如图4所示。由图4可知，原始信号的振动能量主要集中在10 Hz以下，而主频在10 Hz[13-14]以下低频部分是由水流脉冲荷载引起的干扰信息，结构振动信息被低频水流噪声和高频环境噪声所淹没，属于典型的受迫振动响应。对原始信号进行CEEMDAN分解，得到IMF分量C1～C10，各IMF分量的时程图和频谱图，如图5所示。

图2 拉西瓦水弹性模型Fig.2 Hydro-elastic model of Laxiwa

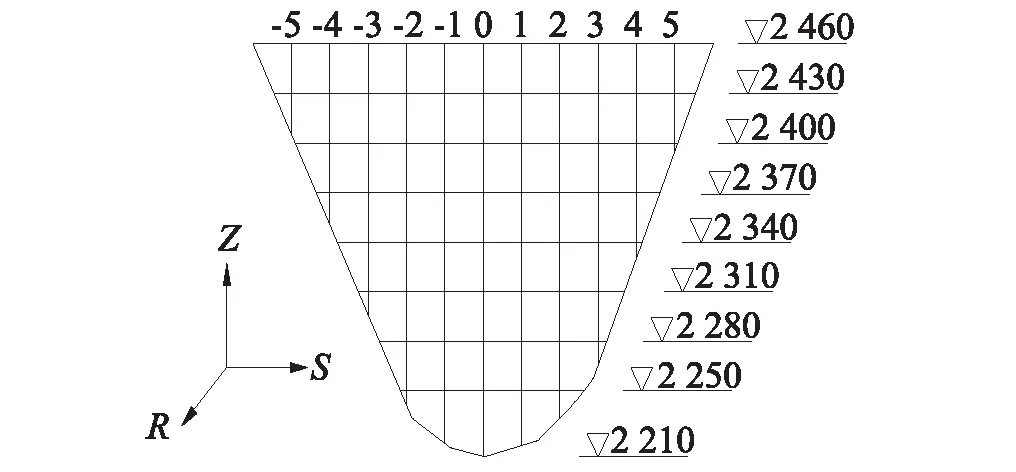
图3 测点布置示意图Fig.3 Measured points arrangement diagram

图4 0测点时程图与功率谱密度曲线图Fig.4 Time history curve and power spectral density curve of measured point 0#

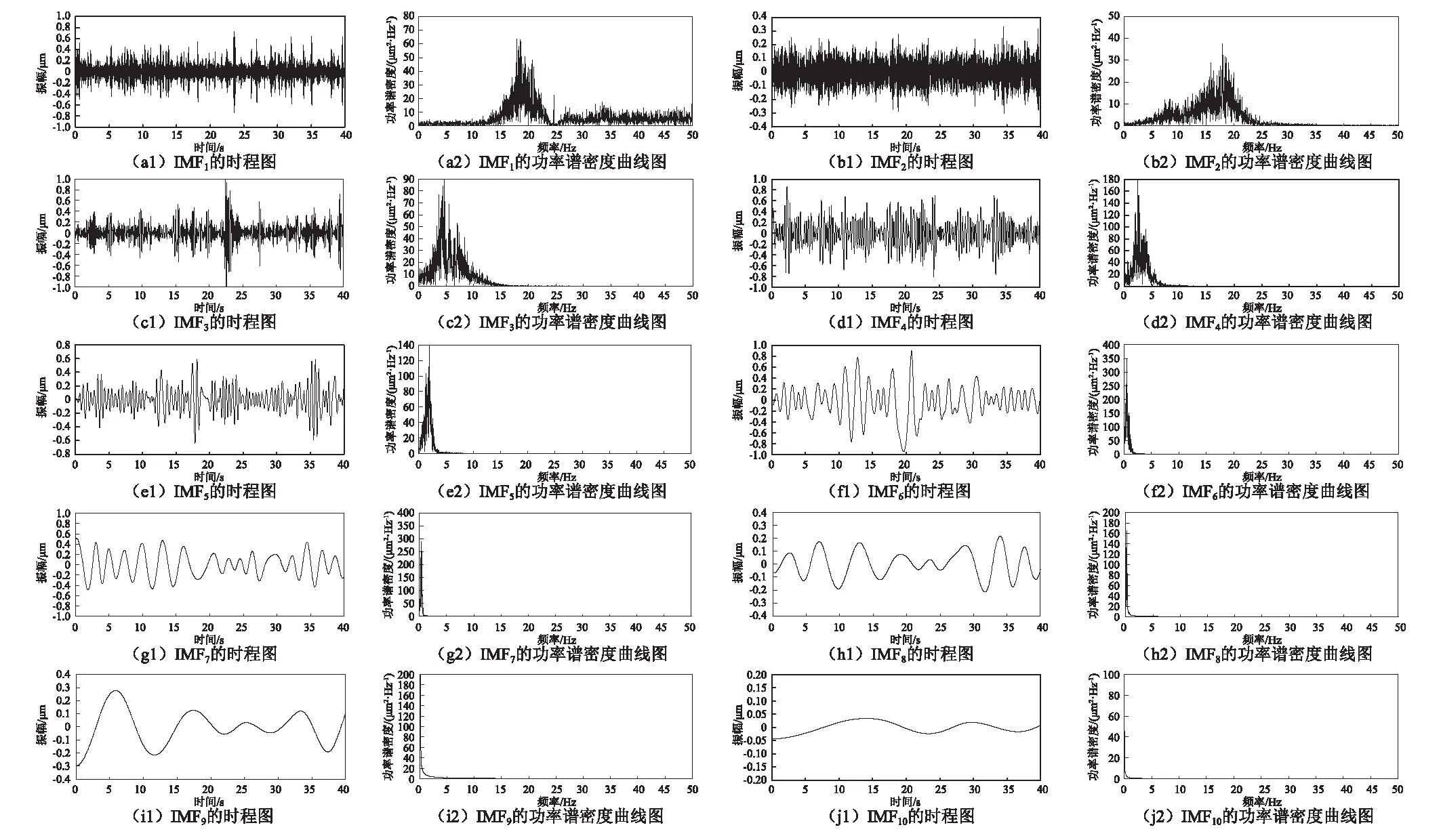
图5 CEEMDAN分解结果Fig.5 The decomposition results of CEEMDAN

由图5可知，分量IMF3～IMF10的频率均小于10 Hz，属于水流脉冲荷载引起的干扰信息，应当滤除，即保留前两阶的IMF。然后对前两阶IMF分量进行排列熵评价，得到的排列熵值为0.687和0.364，根据相关文献的研究成果，需对排列熵值大于0.5的分量进行降噪处理。因此，进一步对IMF1进行奇异值降噪，构造相应的Hankel矩阵进行奇异值分解，得到奇异熵增量曲线如图6所示。从图6可知，在60阶之后，奇异熵增量的值趋于稳定且均小于0.02，根据奇异熵增量理论，可认为前60阶奇异值足以包含信号的特征信息，60阶之后的奇异值是由噪声引起的，保留前60阶奇异值，通过SVD重构得到降噪后的IMF1分量，降噪前后对比图如图7所示。由时空滤波器重构IMF2分量和降噪后IMF1分量，得到滤除高频白噪声和低频水流噪声后的信号，并对信号进行现代功率谱处理，得到较为光滑且反映信号优势频率的频谱图，如图8所示。

图6 奇异熵增量曲线Fig.6 Singular entropy increment

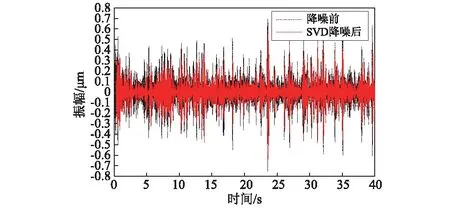
图7 IMF1降噪前后时程图Fig.7 The time history curves of IMF1

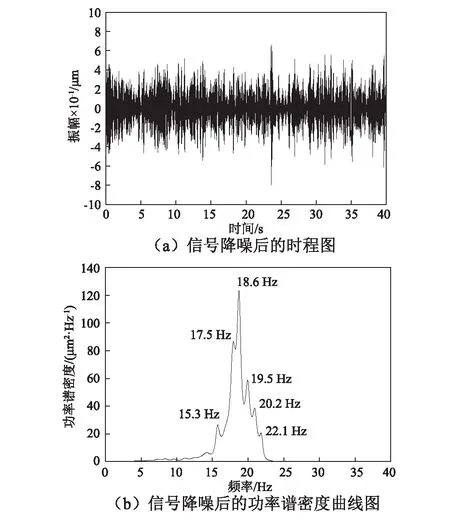
图8 信号降噪后的时程图和功率谱密度曲线图Fig.8 Time history curve and power spectral density curve of signal de-noised by CEEMDAN and SVD

从图8可知，滤波降噪后信号在15.3 Hz、17.5 Hz、18.6 Hz、19.5 Hz、20.2 Hz和22.1 Hz处存在明显峰值，识别结果与文献[15]的辨识结果一致，表明本方法能精确提取泄流结构工作特性信息，具有良好的工程应用性。

为了进一步验证本文降噪方法的有效性和优越性，分别利用CEEMDAN，SVD，CEEMDAN和SVD联合降噪的方法对拉西瓦拱坝的振动信号进行处理。三种方法降噪效果的对比如图9所示。

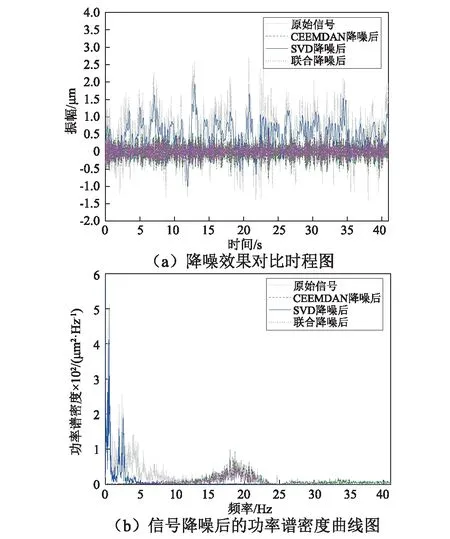
图9 三种方法降噪效果对比图Fig.9 Performance comparison of three de-noising methods

由图9中三种方法的降噪效果对比图可知，相比于其他两种降噪方法，CEEMDAN和SVD联合降噪的效果最好。SVD降噪方法只能滤除高频白噪声，不能滤除低频水流噪声，并且结构的部分有效特征信息也可能被滤除。CEEMDAN降噪方法能够有效地滤除低频水流噪声，但不能滤除高频白噪声，有效特征信息会被高频噪声淹没。而CEEMDAN和SVD联合降噪的方法不仅能最大程度地滤除低频水流噪声和高频白噪声，而且能很好反映结构的有效特征信息。因此，CEEMDAN和SVD联合降噪的方法是一种优越的信号降噪方法，非常适合泄流结构振动信号的降噪。

4 结 论

本文针对泄流结构振动信号的特点，提出一种基于CEEMDAN和SVD联合降噪的结构工作特性信息提取方法。该方法利用排列熵理论对信号复杂度进行评价，联合运用CEEMDAN和SVD对泄流振动信号进行二次滤波降噪，达到凸显信号优势特征、提取结构工作特性信息的目的。拉西瓦拱坝模型分析结果表明：该方法能够精确提取结构的工作特征信息，具有良好降噪能力和工程实用性；作为一种整体的工作特性信息提取方法，该方法具有较高的识别精度，可为泄流结构的安全运行及损伤诊断提供依据。

[ 1 ] 徐国宾,韩文文,王海军，等.水电站泄流诱发厂房结构振动响应预测[J].天津大学学报(自然科学与工程技术版), 2015, 48(3): 196-202.

XU Guobin，HAN Wenwen，WANG Haijun，et al. Prediction of vibration response of powerhouse structures caused by flow discharge[J]. Journal of Tianjin University(Science and Technology), 2015, 48(3): 196-202.

[ 2 ] HUANG N, SHEN Z，LONG S，et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London, Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(3): 903-995.

[ 3 ] 贾瑞生,赵同彬,孙红梅,等. 基于经验模态分解及独立成分分析的微震信号降噪方法[J].地球物理学报, 2015, 58(3): 1013-1023.

JIA Ruisheng, ZHAO Tongbin, SUN Hongmei, et al. Micro-seismic signal denoising method based on empirical mode decomposition and independent component analysis [J]. Chinese Journal of Geophysics, 2015, 58(3): 1013-1023.

[ 4 ] 李琳,张永祥,刘树勇.改进EMD-小波分析的转子振动信号去噪方法[J].噪声与振动控制, 2015, 35(2): 170-174.

LI Lin, ZHANG Yongxiang, LIU Shuyong. Denoising of rotor vibration signals based on improved EMD-wavelet analysis [J]. Noise and Vibration Control,2015,35(2): 170-174.

[ 5 ] 郑近德,程军圣,杨宇. 改进的EEMD算法及其应用研究[J]. 振动与冲击,2013,32(21): 21-26.

ZHENG Jinde, CHENG Junsheng, YANG Yu. Modified EEMD algorithm and its applications[J]. Journal of Vibration and Shock, 2013,32(21): 21-26.

[ 6 ] 陈仁祥,汤宝平,马靖华.基于EEMD的振动信号自适应降噪方法[J].振动与冲击,2012,31(15): 82-86.

CHEN Renxiang，TANG Baoping，MA Jinghua. Adaptive de-noising method based on ensemble empirical mode decomposition for vibration signal [J]. Journal of Vibration and Shock, 2012, 31(15): 82-86.

[ 7 ] 李军,李青. 基于CEEMDAN-排列熵和泄漏积分ESN的中期电力负荷预测研究[J]. 电机与控制学报, 2015,19(8):70-80.

LI Jun, LI Qing. Medium term electricity load forecasting based on CEEMDAN-permutation entropy and ESN with leaky integrator neurons[J]. Electric Machines and Control, 2015,19(8): 70-80.

[ 8 ] 郝旺身,王洪明,董辛旻,等. 基于全矢排列熵的齿轮故障特征提取方法研究[J]. 振动与冲击, 2016, 35(11): 224-228.

HAO Wangshen, WANG Hongming, DONG Xinmin, et al. Gear fault feature extraction based on full vector permutation entropy[J]. Journal of Vibration and Shock, 2016, 35(11): 224-228.

[ 9 ] 程军圣,马兴伟,杨宇.基于排列熵和VPMCD的滚动轴承故障诊断方法[J].振动与冲击,2014, 33(11): 119-123.

CHENG Junsheng, MA Xingwei, YANG Yu. Rolling bearing fault diagnosis method based on permutation entropy and VPMCD [J]. Journal of Vibration and Shock,2014, 33(11): 119-123.

[10] 柴凯,张梅军,黄杰,等.基于奇异值分解(SVD)差分谱降噪和本征模函数(IMF)能量谱的改进Hilbert-Huang方法[J].科学技术与工程,2015,15(9): 90-96.

CHAI Kai, ZHANG Meijun, HUANG Jie, et al. Improved HHT method based on SVD difference spectrum and IMF energy spectrum [J]. Science Technology and Engineering, 2015,15(9): 90-96.

[11] 张建伟,张翌娜,赵瑜.泄流激励下水工结构应变模态参数时域辨识研究[J].水力发电学报,2012,31(3): 199-203.

ZHANG Jianwei, ZHANG Yina, ZHAO Yu. Study on strain modal parameters identification of hydraulic structure in time domain under discharge excitations [J]. Journal of Hydroelectric Engineering, 2012,31(3): 199-203.

[12] 张建伟,李火坤,练继建,等.基于环境激励的厂房结构损伤诊断与安全评价[J].振动、测试与诊断,2012,32(4): 670-674.

ZHANG Jianwei, LI Huokun, LIAN Jijian, et al. Damage diagnosis and safety evaluation of underground powerhouse under ambient excitation[J]. Journal of Vibration, Measurement amp; Diagnosis, 2012,32(4): 670-674.

[13] 李火坤,张建伟,练继建,等.泄流条件下的溢流坝结构原型动力测试与模态参数识别[J].中国农村水利水电, 2009 (12): 99-102.

LI Huokun, ZHANG Jianwei, LIAN Jijian. et al Research on prototype vibration tests and modal parameter identification of the spillway dam under the condition of flood discharge excitation [J]. China’s Rural Water Conservancy and Hydropower, 2009(12): 99-102.

[14] 张建伟,江琦,赵瑜,等.一种适用于泄流结构振动分析的信号降噪方法[J]. 振动与冲击, 2015, 34(20): 179-184.

ZHANG Jianwei, JIANG Qi, ZHAO Yu, et al. A de-noising method for vibration signal of flood discharge structure[J]. Journal of Vibration and Shock, 2015, 34(20): 179-184.

[15] 张建伟.基于泄流激励的水工结构动力学反问题研究[D].天津:天津大学，2008.

Asignalde-noisingmethodforvibrationsignalsfromflooddischargestructuresbasedonCEEMDANandSVD

ZHANGJianwei1，HOUGe1，BAOZhenlei1，ZHANGYina2，MAYing1

(1.SchoolofWaterResources,NorthChinaUniversityofWaterResourcesandElectricPower,Zhengzhou450045,China;2.SchoolofCivilandTransportationEngineering,YellowRiverConservancyTechnicalInstitute,Kaifeng475004,China)

In order to solve the problems that flood non-stationary vibration signals from discharge structures are contaminated by strong noise, a signal de-noising method based on complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) and singular value decomposition (SVD) was proposed. Firstly, the signal was decomposed with CEEMDAN to obtain a series of intrinsic mode functions (IMFs). The spectrum analysis method was used to screen the IMF containing real physical meaning to filter out low frequency noise. Then the permutation entropy theory was used to determine the IMF containing more noise components, and the IMF was used to get appropriate feature matrix with the phase space reconstruction method. A part of white noises were filtered out by SVD and the singular entropy increment theory. Finally the IMF was reconstructed with characteristic information to achieve the de-noised signal through spectrum analysis. The Laxiwa arch dam was used as an example. The results show that the method can filter out vibration noise accurately and retain the characteristic information, which is effective and has highly recognition accuracy. The proposed method can provide help for safe operation and on-line dynamic non-destruction monitoring of flood discharge structures.

flood discharge structure; ensemble empirical mode decomposition; permutation entropy; singular value decomposition; characteristics information

国家自然科学基金(51679091；51408223)；河南省高校科技创新人才计划(18HASTIT012)；广东省水利科技创新基金(2017-16)

2016-06-17 修改稿收到日期： 2016-08-26

张建伟 男，博士，副教授，1979年生

TV93；TB53

A

10.13465/j.cnki.jvs.2017.22.022