基于特征波导纳法和敏感性分析的大型周期支撑结构损伤识别

尹 涛， 尹孟林

(武汉大学 土木建筑工程学院， 武汉 430072)

基于特征波导纳法和敏感性分析的大型周期支撑结构损伤识别

尹 涛， 尹孟林

(武汉大学 土木建筑工程学院， 武汉 430072)

提出了一种基于特征波导纳法和敏感性分析的大型周期支撑结构损伤识别方法。通过分析存在单一损伤单元有限周期支撑结构的自由波传播规律，建立了周期结构无量纲自振频率变化对基本周期单元刚度变化的敏感性分析矩阵；求解敏感性识别方程组，实现基于测量自振频率变化的大型周期支撑结构损伤检测；同时，分析表明所提出无量纲自振频率的敏感性与结构参数无关，即无需知道原始结构的准确几何物理参数就能确定敏感性系数。分别以一周期支撑梁与周期支撑法兰接头管道为例进行研究，表明该方法仅用量测损伤前后的前几阶自振频率变化就能较准确地进行周期支撑结构多损伤识别。

特征波导纳； 敏感性分析； 周期结构； 损伤识别； 法兰连接管道

基于振动的损伤检测方法主要分为基于动力学模型的有模型方法和基于信号分析的无模型方法。其中，无模型方法通常仅能判断损伤发生的部位，而有模型动力检测法则可同时实现损伤部位的判定以及损伤程度的评估，基于敏感性分析的损伤检测方法就是其中重要一类，并受到广泛关注[1]。结构损伤识别中的敏感性分析方法是基于固有模态参数对结构参数变化敏感度的分析计算，判断结构是否出现损伤并确定损伤位置及其程度。该方法的关键在于选取可测且对结构损伤敏感的参数，报道较多的损伤检测参数有结构的固有频率、模态振型以及模态振型曲率等。如Cawley等[2]最早将固有频率敏感性分析运用于结构损伤识别研究，通过固有频率敏感性分析，采用一组非完备的固有频率测量值对简单结构的损伤位置和损伤程度进行了识别。Biswas等[3]利用振型和振型曲率的差异进行损伤定位,取得了一定的效果；Wahab等[4]进一步分析了利用振型进行结构损伤定位的缺陷,提出了基于振型曲率的敏感性参数。薛松涛等[5]推导了结构损伤前后频率变化与结构刚度变化之间的二阶敏感性公式，利用多层框架结构在多种损伤下的振动试验数据确定其损伤位置和程度；Yin等[6]结合自振频率、模态振型及模态应变能的敏感性分析方法与摄动法开展了框架结构的概率损伤识别研究。

上述研究均建立在依据健康结构模型参数获得的模态参数敏感性系数基础上,而对于那些无法准确获知结构几何物理参数的情况，以上方法就存在着较大局限性。此外，实际工程结构如高层建筑、多跨桥梁、长输油气管线以及铁路轨道系统等都可视作由相同子结构首尾串联而成的链状周期结构系统。周期结构动力学分析的显著优势在于，对其自由振动进行精确的波动分析不要求对结构进行完全的模拟[7]，利用周期结构这一特性，可以简化敏感性分析的过程，提高计算效率。朱宏平等[8-9]运用波传播理论得到了周期弹簧-质量系统的频率特征方程，并通过模态参数敏感性分析对多层建筑模型进行损伤识别，但该方法应用范围仅限于能简化为弹簧-质量系统的结构。

本文在朱宏平等的研究基础上，运用波传播理论分析了具有N个基本周期单元的大型周期支撑结构自由振动问题，提出一种无量纲自振频率概念，并得到无量纲自振频率与基本周期单元整体刚度变化率之间的关系。通过建立无量纲自振频率变化率对单元损伤的敏感性识别方程组，并采用约束优化方法求解该识别方程组，以实现周期支撑结构的损伤识别。此外, 本文周期支撑结构无量纲自振频率的敏感性不依赖于结构的具体几何物理参数(如质量密度、弹性模量、结构长度及横截面形状、尺寸等)，具有显著的优越性和实用性。分别通过对一周期支撑梁模型(考虑单元整体刚度降低)和周期支撑法兰管道(仅单元局部刚度降低与附加质量影响)模型的损伤识别数值仿真，对本文方法的正确性和有效性进行验证。

1 理论背景

1.1 单扰乱周期支撑结构频率特征方程建立

图1为含N个基本周期单元的单耦合周期结构，假定其第j个单元为扰乱(或损伤)单元，且记两任意边界分别为C和D。若在结构左端C处施加激励力Fc，则振动波将从点C出发在该结构中传播。当自由波向前传播到达扰乱单元时，将分为两部分：一部分为向激励点反射的反射波，另一部分为越过扰乱单元继续前进的传递波，且传递波继续在扰乱单元右侧传播并在右边界D处产生反射。因此，结构中任意点波动可表示为相应的传递波与反射波之和。设两者在左端C与右端D处的位移分别为XCt、XCr与XDt、XDr，则扰乱单元左右两端A与B处的位移分别表示为

XA-=XA-t+XA-r=XCte-(j-1)μ+XCre(j-1)μ=
αwtFAt+αwrFAr
XB+=XB+t+XB+r=XDte(N-j)μ+XDre-(N-j)μ=
αwtFBt+αwrFBr

(1)

式中：XA-t与XA-r分别为传递波和反射波在节点A处的位移；XB+t与XB+r分别为传递波和反射波在节点B处的位移；FAt、FAr与FBt、FBr分别为传递波与反射波在点A与点B处的广义力，μ为自由波传播常数。αwt和αwr为特征波导纳，其表达式为[10]

αwt=αll-αlre-μ
αwr=αll-αlreμ

(2)

式中，αll和αlr分别为健康周期单元的直接导纳和间接导纳。

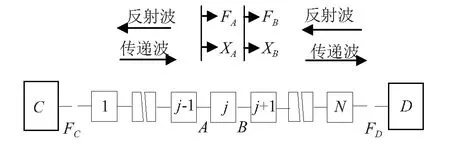
图1 具有单扰乱的单耦合周期系统波传播示意图Fig.1 Wave propagation of mono-coupled periodic structure system with single disorder

扰乱单元j两端点A、点B处的广义力FA、FB可表示为

FA=FAt+FAr
FB=FBt+FBr

(3)

则扰乱单元两端力与位移之间可通过单元导纳联系，即

XA=αAAFA-αABFB
XB=αBAFA-αBBFB

(4)

式中，αAA,αBB和αAB,αBA分别为扰乱单元的直接导纳和间接导纳。

设周期结构右端部D的导纳为αD， 则其位移XD可用力FD和αD表示为

XD=XNt+XNr=αDFD

(5)

依据扰乱单元j两端点A和点B的位移协调与力平衡条件，利用式(1)～式(5)得到周期结构左端点C处反射波和传递波位移X0r和X0t之比为

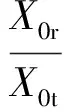
(6)

其中，

(7)

同时，

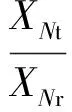
(8)

进一步可得单耦合周期结构中分段表示的任意节点i位移为

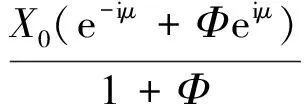
(9)

其中，

g=αwr(αAA-αwt)e-(j-1)μ+αwt(αAA-αwr)e(j-1)μΦ

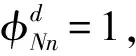
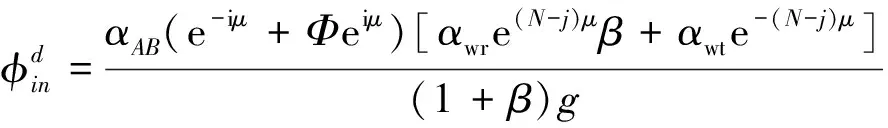
(10)

另，健康状态周期结构需满足以下关系

αAA=αll,αBB=αrr,αAB=αBA=αlr

(11)

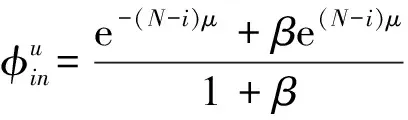
(12)

特别地，在式(9)中，若分母为0，则任意节点处的位移Xi为无限大，即激励频率与结构自振频率相等，产生共振。因此，单扰乱单元周期结构的自振频率可通过式(13)求解

1+Φ=0

(13)

理论上，式(13)中给出的频率特征方程适用于任何存在单扰乱的单耦合周期结构体系，但文献[8]中基于该理论的损伤识别方法仅适用于简单的弹簧-质量系统，应用范围受到较大影响，本文将该理论推广应用于解决更具一般性的大型周期支撑结构损伤识别问题。图2为本文所研究的具有N个基本周期单元的周期支撑结构，其中，将整体结构左端边界C固定以消除结构纵向对称性对损伤识别结果的影响，并假定第j单元为损伤单元，损伤程度以单元整体刚度降低来表征。

图2 左端固定的周期支撑结构Fig.2 Periodically-supported structure with left-end fixed

图2所示结构右端边界D的导纳为αD=∞，将其代入式(8)中可得

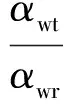
(14)

周期支撑结构的健康周期单元的直接导纳与间接导纳可以分别表示为

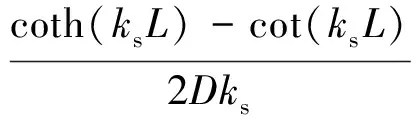
(15)

式中：ks=ω1/2(mb/D)1/4为周期结构波数；D=EI为结构抗弯刚度；E为弹性模量；I为截面惯性矩；ω为自振圆频率；mb为单位长度质量；L为基本周期单元长度。相应地，损伤单元j的单元导纳为

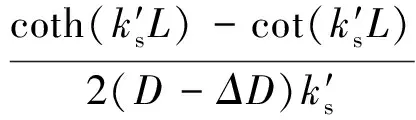
(16)

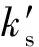
令无量纲自振频率Ω=ksL=ω1/2(mb/D)1/4L， 则损伤前后该无量纲自振频率变化率可表示为

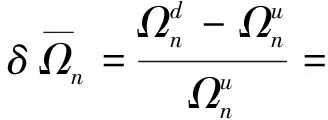
(17)

将式(2)、式(14)、式(15)及γ=iμ代入式(12)中，可得健康周期支撑结构第n阶模态振型为

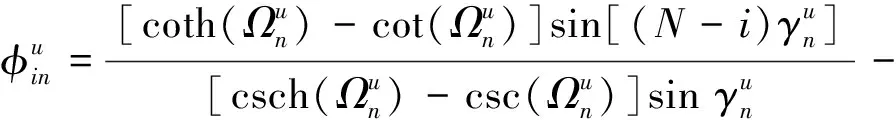
(18)

将式(2)、式(6)、式(7)和式(14)～式(16)及γ=iμ代入式(13)中可得如图2所示周期支撑结构的频率特征方程为

(19)

其中，

A1=a2b-bd2-ac2-b3-2bc2;

B1=a2c-cd2+abc-c3-2b2c;

C1=a2b-bd2-b3-2bc2;D1=c3+2b2c;

A2=bc2;B2=a2c-cd2-b2c;

C2=abc+b2c;D2=ac2-bc2

及

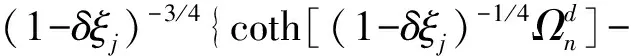
式中：δξj=ΔD/D为损伤单元j在损伤前后的刚度变化率。当δξj=0时，式(19)简化为健康周期支撑结构的频率特征方程

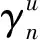
(20)

其中，

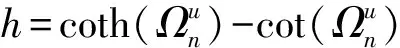
通过该频率方程能计算得到周期支撑结构未损伤时的各阶无量纲频率值。

1.2 周期支撑结构无量纲频率的敏感度系数

周期支撑结构波传播常数与周期结构单元导纳之间的关系为[11]

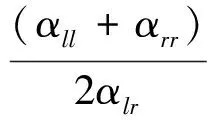
(21)

将式(15)代入式(21)中得

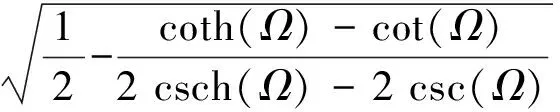
(22)

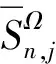
(23)

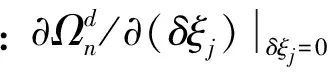
表1 健康周期支撑结构的前5阶无量纲频率值

图3 10单元周期支撑结构各阶无量纲频率敏感度系数Fig.3 Sensitivities of non-dimensional frequencies for the first five modes of periodically-supported structures with 10 cell elements

在多单元损伤情况下，任意阶无量纲自振频率变化可视作单损伤引起频率变化的线性叠加，若忽略高次项，则损伤引起的无量纲频率总变化率为

(24)

即

(25)

式中：p为周期结构测量模态阶数； [S]为无量纲频率的敏感性矩阵。

通常测量获得的结构自振频率阶数要少于周期支撑结构单元总数(即plt;N)，这会导致式(25)中的敏感性识别方程组欠定，造成求解结果不唯一。为此，考虑到损伤不可能引起刚度增加，将本文周期支撑结构的损伤识别问题转化成如下的非负最小二乘曲线拟合问题

(26)

运用适合该类问题的数值优化算法[12]求解式(26)，可得到周期支撑结构损伤识别结果。

2 数值仿真研究

本节通过一个周期支撑梁与周期支撑法兰管线损伤识别算例对本文方法进行验证。

2.1 周期支撑梁模型数值仿真

考虑图2所示的10单元周期支撑梁模型，其中，通过降低某基本周期单元的弹性模量来模拟该单元的整体刚度降低。假定该周期梁模型为矩形截面，宽、高均为0.03 m，基本周期单元(两相邻支座之间或支座与固定端之间)的长度为0.5 m，整体结构总长为5 m，密度为2.7×103kg/m3，泊松比为0.3，弹性模量为71 GPa。待识别损伤位置个数为10，分别为各基本周期单元的弹性模量，而损伤识别仅利用前5阶模态频率，以模拟实际应用中仅较少阶模态可测情况。

对于该周期支撑梁模型，共考虑4种损伤工况，其中包含单损伤和双损伤工，各工况具体损伤位置及损伤程度见表2。此外，表3为各损伤工况对应的损伤前后前5阶无量纲自振频率变化率，从表3可知，损伤引起的无量纲频率改变较小，且不同模态对于损伤敏感程度不一样，其中第1阶和第5阶频率对于损伤较为敏感。本例损伤识别过程中，为模拟自振频率测量噪声影响，在损伤前后的真实自振频率中均考虑了标准差为1%的高斯白噪声。无测量噪声及考虑测量噪声情况下的损伤识别结果，如图4和图5所示，从图可知，本文方法在两种情况下均能较正确识别损伤位置及相应损伤程度。此外，两图的损伤识别结果也同样反映出，无噪声情况下损伤程度识别值与预设损伤约有20%的差别，噪声工况下该差别更明显。

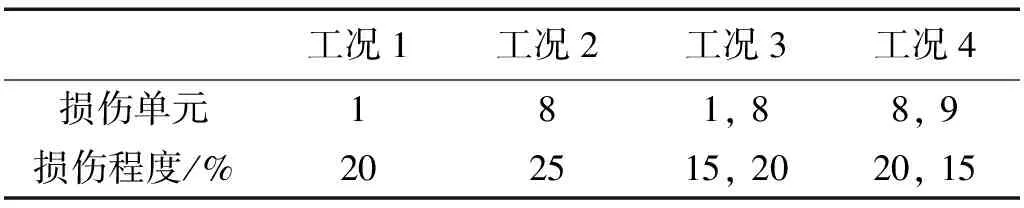
表2 周期支撑梁模型损伤工况

表3 周期支撑梁模型损伤前后前5阶无量纲频率变化率

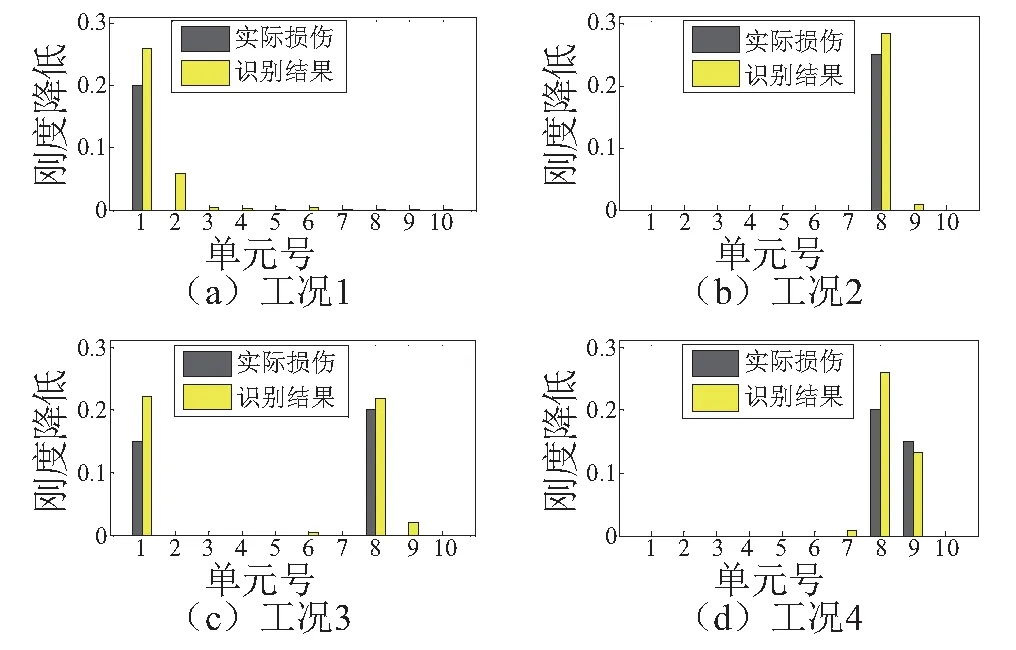
图4 无测量噪声情况下周期支撑梁的损伤识别结果Fig.4 Identified damage for the periodically-supported beam model without noise

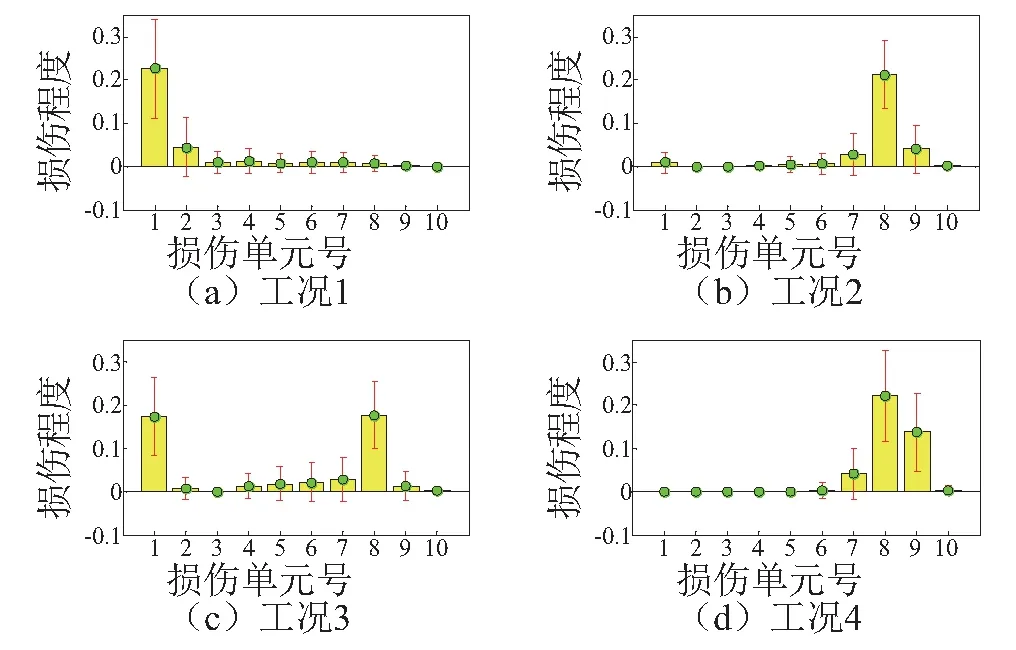
图5 考虑测量噪声情况下周期支撑梁的损伤识别结果的误差棒图Fig.5 Error bars of identified damage for the periodically-supported beam model with measurement noise

2.2 周期支撑法兰管线模型数值仿真

为进一步验证本文周期支撑结构敏感性损伤识别方法对于更一般实际工程结构的适用性，具有10个周期单元的周期支撑法兰连接管线模型，其左端C设为固定边界，如图6(a)所示。其中，将相邻两支座之间的法兰管道视作一个基本周期单元，如图6(b)所示。且规定左固定端与相邻支座之间部分为1号周期单元。

假定法兰盘之间通过螺栓连接，为简化建模分析，将两对接法兰之间的螺栓连接简化为薄层单元，即各基本周期单元的中间部分变为含薄层单元的法兰接头，见图6(b)。在管道结构健康状态下，各法兰接头中间薄层单元的弹性模量相等。通过降低某薄层单元的弹性模量，也即降低该法兰薄层所在基本周期单元的局部刚度，以模拟实际管线工程中螺栓法兰连接因螺栓松动而导致的局部刚度降低。

(a) 周期支撑法兰管道模型示意

(b) 基本周期单元图6 周期支撑法兰管道简化模型与其基本周期单元Fig.6 Schematic model for periodically-supported flanged pipeline and its cell element

本周期支撑法兰管道横截面为圆形，管道内外径分别为0.081 m与0.089 m，法兰外径为0.18 m，法兰厚度为0.02 m。相邻法兰接头之间的管道长度为1 m，而整体模型最左端与最右端的管道长度均为0.5 m，如图6(a)所示。假定每对法兰配置6根M16×80 mm螺栓，两对接法兰盘面中间薄层部分厚度假定为0.004 6 m，弹性模量与质量密度依据文献[13]方法确定。管道与法兰材料相同，其弹性模量与质量密度均分别为68.7 GPa和2.8×103kg/m3，泊松比为0.33。图7表示依据上述几何材料参数与边界条件建立的10周期的法兰管道实体有限元模型。

针对该法兰接头管线模型，共考虑了4种损伤工况，如表4所示。其中，前两种工况为单损伤，后两种工况考虑双损伤，且通过将各对应损伤法兰接头中间薄层单元弹性模量降低50%以模拟螺栓松动引起的管线局部法兰接头损伤。表5为通过图7所示实体有限元模型计算得到的周期支撑法兰接头管线各工况下损伤前后前5阶无量纲自振频率变化率，且后续损伤识别过程仅利用该前5阶无量纲频率改变，以模拟实际工程应用中仅较少阶模态可测的情况。

表4 周期支撑法兰管道模型损伤工况

表5 周期法兰管线模型伤前后前5阶无量纲频率变化率

图7 含薄层单元的法兰管道有限元模型Fig.7 FE model for periodically-supported flanged pipeline

应指出，本例所考虑的法兰接头损伤与前例中的周期支撑梁结构有所不同。前例中周期支撑梁考虑理论化的基本周期单元整体刚度降低，而本例考虑更为实际的周期单元内的局部刚度降低，且同时考虑法兰接头附加质量的影响。因而，前例中的识别损伤程度能与事先指定的真实值定量比较，而本法兰管线算例中的识别损伤程度仅能相对表征。同样地，损伤前后真实自振频率均考虑了1%的高斯白噪声影响，采用本文方法得到各损伤工况无噪声与有噪声情况下对应的识别结果，如图8和图9所示。从两情况识别结果中可知，对于单元局部损伤且考虑法兰接头附加质量的周期支撑法兰管线，各损伤工况下均能较准确地识别出损伤位置及相对损伤程度，表明本文方法具有较强的适用性。

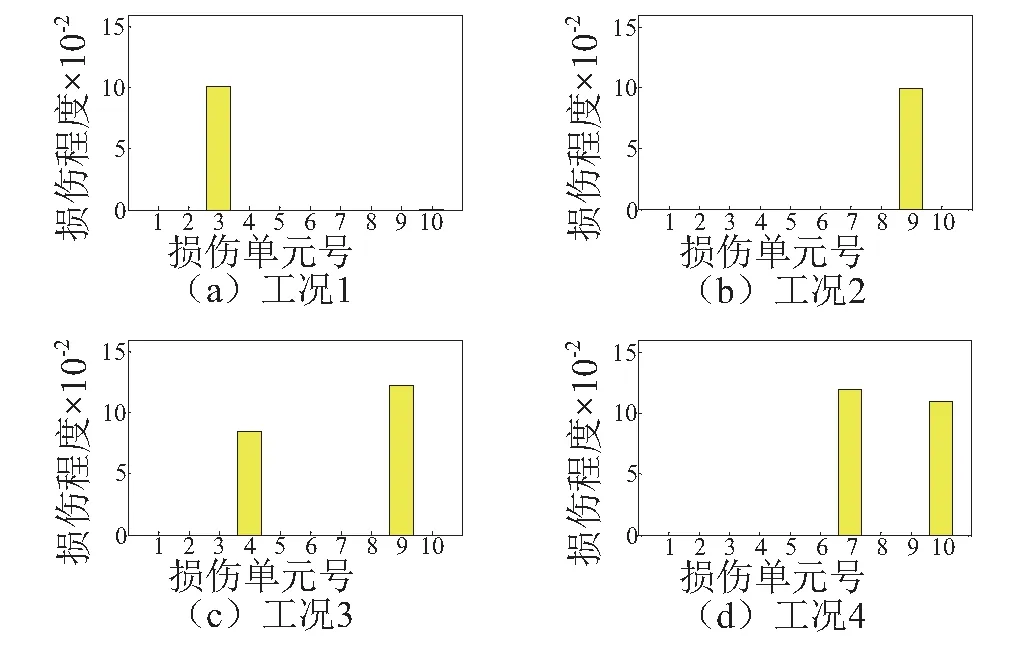
图8 无测量噪声情况下周期支撑法兰管道损伤识别结果Fig.8 Identified damage for the periodically-supported flanged pipeline model without noise

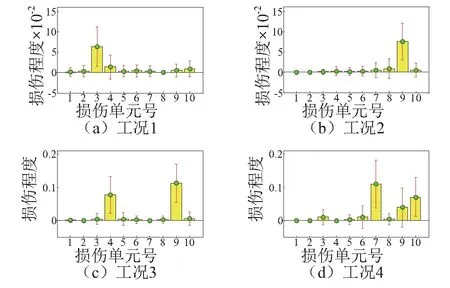
图9 考虑测量噪声情况下周期支撑法兰管道损伤识别结果的误差棒图Fig.9 Error bars of identified damage for the periodically-supported flanged pipeline model with measurement noise

3 结 论

本文基于特征波导纳和敏感性分析法得到有限长周期支撑结构无量纲自振频率敏感性矩阵的通用表达式，进而建立了一种有效的周期支撑结构敏感性动力损伤识别方法。研究表明，充分利用周期支撑结构的固有周期特性，获得的无量纲自振频率敏感性矩阵仅与周期单元总数和结构损伤位置有关，而与结构其它几何物理参数如密度、弹性模量、长度、横截面尺寸以及横截面形状等无关，极大地简化了复杂周期支撑结构特征值敏感性分析过程，避免了对于结构准确模型参数的依赖，显著提高了本文损伤识别方法的实用性。对一周期支撑梁与周期支撑法兰管线模型的多种损伤工况识别表明，本文方法均能较准确识别出损伤位置与损伤程度。

应指出，本文损伤识别方法基于周期支撑结构中基本周期单元整体刚度下降基础上推导得来，因而，对于周期支撑梁算例中基本周期单元的整体刚度下降，本文方法能给出较准确的损伤程度估计，而对于基本周期单元的局部刚度降低，本文方法也能较准确地给出各位置的相对损伤程度，表明本文方法具有较好的适用性和扩展性。此外，也应注意到，尽管对于损伤位置判定较准确，但本文基于一阶固有频率敏感性分析的损伤识别方法对于损伤程度的准确估计仍显不足，因此，进一步优化损伤敏感性参数与运用高阶敏感性分析技术有助于提高本文方法对于损伤程度估计的准确性。

[ 1 ] ZHAO J, DEWOLF J T. Sensitivity study for vibrational parameters used in damage detection[J]. Journal of Structural Engineering, 1999, 125(4): 410-416.

[ 2 ] CAWLEY P, ADAMS R D. The location of defects in structures from measurements of natural frequencies[J]. Journal of Strain Analysis for Engineering Design, 1979, 14(2): 49-57.

[ 3 ] BISWAS M, PANDEY A K, SAMMAN M M. Diagnostic experimental spectral/modal analysis of a highway bridge[J]. International Journal of Analytical amp; Experimental Modal Analysis, 1990, 5(1): 377.

[ 4 ] WAHAB M M A, ROECK G D. Damage detection in bridges using modal curvatures: application to a real damage scenario[J]. Journal of Sound and Vibration, 1999, 226(2): 217-235.

[ 5 ] 薛松涛, 钱宇音, 陈镕, 等. 采用二阶频率灵敏度的损伤识别和试验[J]. 同济大学学报(自然科学版), 2003, 31(3): 263-267.

XUE Songtao, QIAN Yuyin, CHEN Rong, et al. Damage identification and experiments of frame structure based on second-order rrequency sensitivity[J]. Journal of Tongji University (Natural Science), 2003, 31(3): 263-267.

[ 6 ] YIN Tao, ZHU Hongping, YU Ling. Noise analysis for sensitivity-based structural damage detection[J]. Applied Mathematics and Mechanics, 2007, 28(6): 741-750.

[ 7 ] 朱宏平, 何波. 基于敏感性分析的周期结构损伤检测[J]. 工程力学, 2003, 20(3): 108-114.

ZHU Hongping, HE Bo. Damage detection in periodic structures based on a sensitivity method[J]. Engineering Mechanics, 2003, 20(3): 108-114.

[ 8 ] ZHU H, WU M. The characteristic receptance method for damage detection in large mono-coupled periodic structures[J]. Journal of Sound and Vibration, 2002, 251(2): 241-259.

[ 9 ] ZHU H P, XU Y L. Damage detection of mono-coupled periodic structures based on sensitivity analysis of modal parameters[J]. Journal of Sound and Vibration, 2005, 285(1/2): 365-390.

[10] MEAD D J, BANSAL A S. Mono-coupled periodic systems with a single disorder: free wave propagation[J]. Journal of Sound and Vibration, 1978, 61(4): 481-496.

[11] MEAD D J. Wave propagation and natural modes in periodic systems: I. Mono-coupled systems[J]．Journal of Sound and Vibration, 1975, 40(1): 1-18.

[12] LAWSON C L, HANSON R J. Solving least squares problems[M]. Englewood Cliffs: Prentice-hall, 1974.

[13] 姜东，吴邵庆，史勤丰，等．基于各向同性本构关系薄层单元的螺栓连接参数识别[J]. 振动与冲击, 2014, 33(22): 35-40.

JIANG Dong, WU Shaoqing, SHI Qinfeng, et al. Parameter identification of bolted-joint using thin-layer element with isotropic constitutive relationship[J]. Journal of Vibration and Shock, 2014, 33(22): 35-40.

Damagedetectioninlargeperiodically-supportedstructuresbasedonthecharacteristicreceptancemethodandthesensitivity-basedapproach

YIN Tao， YIN Menglin

(School of Civil Engineering, Wuhan University, Wuhan 430072, China)

This paper developed a novel damage detection method for large periodically-supported structures based on the characteristic receptance method and the sensitivity analysis technique. By analyzing the free vibration of a finite periodically-supported structure with a single disorder based on the wave propagation method, the sensitivity matrix of the non-dimensional natural frequencies with respect to the change in element stiffness was obtained. And then, the damage scenarios in large periodically-supported structures were identified with the damage induced changes of natural frequencies by solving a set of underdetermined equations based on the sensitivity matrix. Furthermore, it was found that the sensitivities of the non-dimensional natural frequencies are independent of the structural physical parameters and thus any prior information of the original structures is never required. The proposed method is demonstrated by the numerical case studies conducted for both a periodically-supported beam and a periodically-supported flanged pipeline with various damage scenarios by utilizing only the frequency measurements for the first few modes before and after damage.

characteristic receptance; sensitivity analysis; periodic structures; damage detection; flanged pipeline

国家自然科学基金(51778506)

2016-05-10 修改稿收到日期： 2016-08-03

尹涛 男，博士，副教授，1979年生

O327

A

10.13465/j.cnki.jvs.2017.22.015