基于改进尾流振子模型的柔性圆柱体涡激振动响应特性数值研究

高 云, 谭 暖, 熊友明, 邹 丽, 宗 智

(1. 西南石油大学 油气藏地质及开发工程国家重点实验室，成都 610500; 2. 东京大学 机械工程学院，东京 113-86563. 大连理工大学 船舶工程学院，辽宁 大连 116024)

基于改进尾流振子模型的柔性圆柱体涡激振动响应特性数值研究

高 云1,2, 谭 暖1, 熊友明1, 邹 丽3, 宗 智3

(1. 西南石油大学 油气藏地质及开发工程国家重点实验室，成都 610500; 2. 东京大学 机械工程学院，东京 113-86563. 大连理工大学 船舶工程学院，辽宁 大连 116024)

基于改进的尾流振子模型对柔性圆柱体涡激振动响应特性进行了数值研究，先分别建立了柔性圆柱体结构振子模型以及尾流振子模型，随后将二振子模型进行耦合。研究中通过改变无量纲张力、细长比以及质量比等无量纲参数，对柔性圆柱体的振幅比、相位角、频率比以及位移响应时间特性等参数进行了分析。分析结果表明：柔性圆柱体涡激振动响应特性呈现典型的行波特性，行波传播速度随着无量纲张力的增加而呈现上升趋势；行波传播速度随着细长比的增加呈下降趋势。随着无量纲张力以及细长比的增加，位移与升力之间的相位角会发生突变，突变点均发生在振动频率经过固有频率处。

柔性圆柱体； 尾流振子模型； 数值研究； 行波； 相位角

柔性圆柱体在一定的来流下，会在其两侧形成交替脱落的漩涡，漩涡脱落会引起圆柱体产生周期性的振动，称为涡激振动(Vortex Induced Vibration, VIV)[1]。当漩涡脱落频率接近圆柱体固有频率时，便会发生锁定(lock-in)。锁定区域内，圆柱体会发生大幅的、危险的涡激振动响应，这种响应会对结构带来很大的疲劳损伤。

现有的研究圆柱体涡激振动响应的方法主要有实验方法[2-5]、计算流体动力学(Computational Fluid Dynamics, CFD)方法[6-8]以及经验模型方法。对于柔性圆柱体，由于其结构轴向尺寸较大，使得在整个流场区域内展开全尺度涡激振动位移响应时域模拟非常困难，目前的CFD计算水平很难达到这种计算需求。实验方法本身存在很多优点，如分析数据可靠、分析现象直观等；但实验方法通常研究成本较高。基于此，使用经验模型方法来研究圆柱体的涡激振动响应特性得到了国内外诸多学者的关注，而尾流振子模型法则是经验模型方法中应用较为广泛的一种数值方法。表1给出了近几十年国内外使用尾流振子模型来预测圆柱体涡激振动响应特性的研究[9-21]。

表1 基于尾流振子模型的圆柱体涡激振动响应相关研究

由表1可知：①尾流振子模型已广泛应用于空气以及水中的圆柱体涡激振动响应研究，圆柱体包括刚性圆柱体以及柔性圆柱体；②尾流振子模型除了在均匀流中得到了普遍应用以外，在剪切流以及阶梯流等非均匀流中同样得到了一定范围的应用。从目前的国内外研究现状来看，针对柔性圆柱体的涡激振动响应特性，尚存在很多问题需要更为深入的研究。比如：ⓐ 柔性圆柱体涡激振动响应特性通常呈现出很明显的行波特性，那么随着张力、细长比以及质量比的增加，这种行波特性呈现怎样的变化趋势？ⓑ 柔性圆柱体的涡激振动位移响应又是怎样随着张力、细长比以及质量比的变化而发生变化的？ⓒ 柔性圆柱体涡激振动响应位移与升力之间始终存在一个相位差，相位差是怎样随着张力、细长比以及质量比的变化而发生变化的？

基于以上问题，本文基于改进的尾流振子模型对柔性圆柱体涡激振动响应特性展开了系统的数值研究。研究内容如下：先建立柔性圆柱体结构振子以及尾流振子之间的耦合方程，然后通过解耦分析得到圆柱体涡激振动位移响应以及升力表达式。通过与多位研究者的分析结果进行对比验证了本文数值模型的可靠性。依次展开了张力、细长比以及质量比对柔性圆柱体涡激振动响应特性影响的研究。

1 分析模型

1.1 柔性圆柱体结构振子模型

如图1所示，考虑一个无限长的细长柔性圆柱体在均匀来流作用下引起的横流方向涡激振动响应问题。本文在无限长的圆柱体上截取典型样本段L作为研究对象，L两端采取周期性边界条件。取坐标原点O为L段的下端，X方向为顺流方向，Z方向为铅直方向，X,Y以及Z三个方向形成右手直角坐标系。柔性圆柱体上受到的张力为Θ，来流大小为U。

图1 稳定均匀流中的细长柔性圆柱体模型Fig.1 A flexible cylinder subjected to a stationary uniform flow

将细长柔性圆柱体看作张力索模型，其振动方程可表示为

(1)

式中：Y(Z,T)为T时刻坐标位置为Z处的涡激振动位移响应；P(Z,T)为升力分布，可表示为[22]

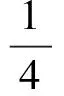
(2)

式中：q(Z,T)为尾流振子的运动；CL0为横向升力系数，这里CL0=0.3[23]。式(1)中柔性圆柱体单位长度质量m包括结构质量ms和附加流体质量mf，可表示为

m=ms+mf,mf=CMρD2π/4

(3)

式中：ρ为流体密度；D为柔性圆柱体的直径；CM为附加质量系数，CM=1.0[24]。 式(1)中阻尼R包括结构阻尼Rn和流体阻尼Rf，可表示为

R=Rn+Rf,Rf=γωfρD2

(4)

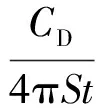
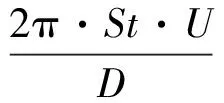
(5)

1.2 尾流振子模型

采用改进的Van der pol方程来满足尾流振子的非线性特性[25]，表达式为

(6)

q(Z,T)与结构升力系数有关，可定义为

(7)

式中：ε为非线性项中的小参数；A为结构对流体的耦合动力参数。参数ε和结构对流体的耦合作用力系数A的值分别取为：ε=0.3，A=12；CL为流体对结构的瞬时升力系数。

1.3 柔性圆柱体和尾流振子耦合

将式(1)和式(6)转换成无量纲形式。则令

y=Y/D,z=Z/D,t=T·ωf

(8)

将这三个等式分别代入式(1)和式(6)中，整理得到无量纲方程为

(9)

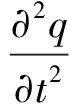
(10)

(11)

当结构振动频率ωv、漩涡脱落频率ωf以及结构固有频率ωn接近时，结构与流体之间会发生锁定现象。在锁定区域内,ωv=ωf，但由于结构与流体之间的非线性相互作用，最大稳态振幅通常并不发生在ωv(ωf)与ωn相等处，而是发生在锁定区域的中段，这种现象称之为失谐。因此引入失谐参数ω，并表示为

(12)

考虑上述流固耦合问题，假设式(9)和式(10)的解为

y(z,t)=y0·cos(kz-ωt-φ)

(13)

q(z,t)=q0cos(kz-ωt)

(14)

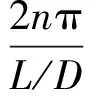
(15)

(16)

将式(13)和式(14)代入式(10)，并进行整理得到

(17)

ω6-[1+2c2k2-(2ξδ+γ/μ)2-AM]ω4-
[-2c2k2+(2ξδ+γ/μ)2-c4k4+AMc2k2]ω2-
c4k4=0

(18)

那么得到结构振动的位移及升力振子表达式为

(19)

(20)

可根据式(18)求得ω的值，进一步结合式(19)和式(20)计算出结构的振动位移和升力振子的值。

2 数值模型验证

为了验证本文尾流振子模型的可靠性，这里进行了数值验证，验证过程中选取了与文献[26]中相同的参数进行了计算，然后将计算结果与他人计算结果[27]进行了对比。图2给出了使用本文模型计算得到的以及他人计算得到的涡激动振动位移响应对比云图；表2给出了最大无量纲位移对比结果。由图3和表2可知，本文数值模型的计算结果与其他研究者的计算结果吻合良好，从而验证了本文数值模型的可靠性。

图2 涡激振动位移响应对比Fig.2 Comparison of VIV displacement response

表2 本文模型计算结果与其他研究者的研究结果对比

3 分析与讨论

本文计算工况如表3所示，讨论了无量纲张力、细长比以及质量比这三个参数对柔性圆柱体涡激振动响应特性的影响，共计算了48种工况。

表3 计算工况

3.1 张力的影响

图3给出了不同无量纲张力下的最大无量纲振幅比、相位角以及频率比。由图3可知，随着无量纲张力的增加，无量纲振幅比呈现先上升再下降的趋势，且最大无量纲振幅比0.58出现在无量纲张力为三处。

(a) 振幅比

(b) 相位角

(c) 频率比图3 不同无量纲张力下的最大无量纲振幅比、相位角以及频率比Fig.3 The maximum value of non-dimensional displacement, phase angle and frequency ratio at different non-dimensional tension

当无量纲张力从1增加到3.7(图3中A点所示)时，升力与位移之间的相位角φ呈现逐渐上升的趋势；当无量纲张力继续增加到4(图3中B点所示)时，φ发生了突降，此时对应的频率比刚好经过1，意味着此时振动频率ωv刚好经过固有频率ωn； 随着无量纲张力的进一步增加，当从4增加到6时，φ再次呈现逐渐上升的趋势。随着无量纲张力的增大频率比是先缓慢下降再迅速上升的趋势。

图4进一步给出了相位角发生突变前后两点A点和B点对应的位移响应以及升力响应时间历程。A点处，位移与升力之间的相位角为正相位83.01°；从A点变到B点处，相位角发生了突变，由正相位83.01°变成了负相位90°。

图5给出了4种不同张力下柔性圆柱体的涡激振动位移响应云图以及无量纲振幅比均方根值。由图5可知，柔性圆柱体的涡激振动位移响应呈现典型的行波特性，且随着张力增加行波的传播速度越来越快。当无量纲张力为3时，无量纲行波速度为3.59；当无量纲张力增加到6时，无量纲行波速度上升为8.37。

图4 位移以及升力时间历程曲线Fig.4 Time series of displacement and lift force

图5 不同无量纲张力下位移响应变化云图以及无量纲振幅比均方根值Fig.5 Time series of displacement fluctuation and RMS values of non-dimensional displacements at different non-dimensional tension

3.2 细长比的影响

图6给出了不同细长比下对应的最大无量纲振幅比、相位角以及频率比。由图6可知，随着细长比的增加，无量纲振幅比呈现先迅速上升再趋于稳定的趋势，且最大无量纲振幅比0.584出现在细长比10.8π处。

当细长比从6π增加到8π时，升力与位移之间的相位角φ呈现逐渐下降趋势；当无量纲张力从8π(图6中A点所示)增加到8.4π(图6中B点所示)时，相位角φ发生了突变，由负相位变成了正相位；随着细长比的进一步增加，当从8.4π增加到14π时，φ再次呈现逐渐下降的趋势。频率比随着细长比的上升呈下降趋势。图7进一步给出了相位角发生突变前后两点A点和B点对应的位移时间曲线以及升力时间曲线。A点处，位移与升力之间的相位角为负相位90°；从A点变到B点处，相位角发生了突变，由负相位90°变成了正相位85.49°。

图8给出了4种不同细长比下柔性圆柱体的涡激振动位移响应云图以及无量纲振幅比均方根值。由图8可知，柔性圆柱体的涡激振动位移响应呈现行波特性，且随着圆柱体细长比的增加，行波传播速度越来越慢。当细长比为6π时，无量纲行波速度为4.71；当细长比增加到12π时，无量纲行波速度下降为3.77。

图6 不同细长比下的最大无量纲振幅比、相位角以及频率比Fig.6 The maximum value of non-dimensional displacement, phase angle and frequency ratio at different aspect ratio

图7 位移以及升力时间历程曲线Fig.7 Time series of displacement and lift force

图8 不同细长比下位移响应变化云图以及无量纲振幅比均方根值Fig.8 Time series of displacement fluctuation and RMS values of non-dimensional displacements at different aspect ratio

3.3 质量比的影响

图9给出了不同质量比下对应的最大无量纲振幅比、相位角以及频率比。由图9可知，随着质量比的增加，无量纲振幅比呈下降趋势，升力与位移之间的相位角φ也呈下降趋势，意味着：位移与升力之间的相位没有发生突变，始终保持同相位。随着质量比的增大，频率比呈现先快速下降再缓慢上升的趋势。

图10给出了不同质量比下柔性圆柱体的涡激振动位移响应云图以及无量纲振幅比均方根值。由图10可以看出: 随着圆柱体质量比的增加，柔性圆柱体的涡激振动位移响应行波传播速度逐渐变小，但是变化幅值比较缓慢。当质量比为0.785时，无量纲行波速度为5.23；当质量比增加到2.785时，无量纲行波速度下降为3.93。

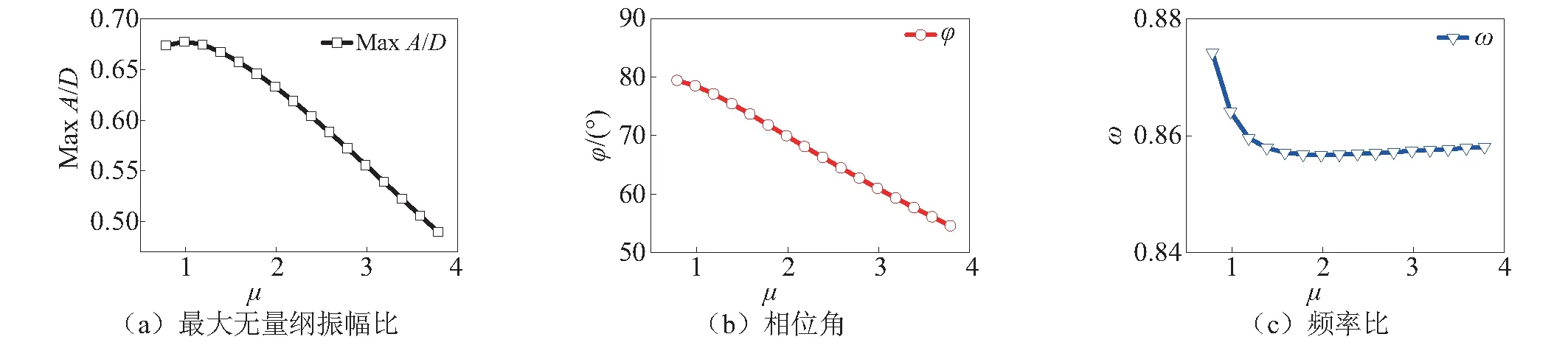
图9 不同质量比下的最大无量纲振幅比、相位角以及频率比 Fig.9 The maximum value of non-dimensional displacement, phase angle and frequency ratio at different mass ratio

图10 不同质量比下无量纲振幅比时间历程云图以及无量纲振幅比均方根值Fig.10 Time series of displacement fluctuation and RMS values of non-dimensional displacements at different mass ratio

4 结 论

本文基于尾流振子模型对柔性圆柱体的涡激振动响应特性进行了数值研究，系统地研究了不同无量纲张力、不同细长比以及不同质量比下柔性圆柱体的涡激振动响应特性，通过研究得到如下结论：

(1) 柔性圆柱体的涡激振动响应特性呈现典型的行波特性，行波传播速度随着无量纲张力的增加逐渐上升；传播速度随细长比的增加而逐渐下降；传播速度随着质量比的增加同样呈下降趋势，但下降速度非常缓慢。

(2) 随着无量纲张力的增加，柔性圆柱体的涡激振动位移响应呈现先上升后下降的趋势，最大位移响应出现在无量纲张力为三处；随着细长比的增加，涡激振动位移响应呈现先迅速上升再趋于稳定的趋势；随着质量比的增加，涡激振动位移响应呈下降趋势。

(3) 随着无量纲张力以及细长比的增加，柔性圆柱体的涡激振动位移响应与升力响应之间的相位角均会发生相位突变，且突变点发生在涡激振动位移响应频率经过结构固有频率处。

[ 1 ] BLEVINS R D. Flow-induced vibration [M]. 2nd ed. Malabar: Krieger Publishing, 2001.

[ 2 ] 张永波, 郭海燕, 孟凡顺, 等. 基于小波变换的顶张力立管涡激振动规律实验研究 [J]. 振动与冲击, 2011, 30(2): 149-154.

ZHANG Yongbo, GUO Haiyan, MENG Fanshun, et al. Model tests for vortex-induced vibration of a top tension riser based on wavelet transformation [J]. Journal of Vibration and Shock, 2011, 30(2): 149-154.

[ 3 ] 康庄, 贾鲁生. 圆柱体双自由度涡激振动轨迹的模型试验 [J]. 力学学报, 2012, 44(6): 970-979.

KANG Zhuang, JIA Lusheng. An experiment investigation on VIV trajectories of a two degree free vibration cylinder [J]. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(6): 970-979.

[ 4 ] 高云, 任铁, 付世晓, 等. 柔性立管涡激振动响应特性试验研究 [J]. 振动与冲击, 2015, 34(17): 6-11.

GAO Yun, REN Tie, FU Shixiao, et al. Tests for response characteristics of VIV of a flexible riser [J]. Journal of Vibration and Shock, 2015, 34(17): 6-11.

[ 5 ] CHEN W L, ZHANG Q Q, LI H, et al. An experimental investigation on vortex induced vibration of a flexible inclined cable under a shear flow [J]. Journal of Fluids and Structures, 2015, 54: 297-311.

[ 6 ] 唐友刚, 樊娟娟, 张杰, 等. 高雷诺数下圆柱顺流向和横流向涡激振动分析 [J]. 振动与冲击, 2013, 32(13): 88-92.

TANG Yougang, FAN Juanjuan, ZHANG Jie, et al. In line and transverse vortex-induced vibration analysis for a circular cylinder under high Reynolds number [J]. Journal of Vibration and Shock, 2013, 32(13): 88-92.

[ 7 ] ZHANG H, FAN C F, CHEN Z H, et al. An in-depth study on vortex-induced vibration of a circular cylinder with shear flow [J]. Computers and Fluids, 2014, 100: 30-44.

[ 8 ] ZHAO M, CHENG L, AN H W, et al. Three-dimensional numerical simulation of vortex-induced vibration of a elastically mounted rigid circular cylinder in steady current [J]. Journal of Fluids and Structures, 2014, 50: 292-311.

[ 9 ] GRIFFIN O M. Vortex-excited cross-flow vibrations of a single cylindrical tube [J]. Journal of Pressure Vessel Technology, 1980,102(2): 158-166.

[10] BASU R I, VICKERY B J. Across-wind vibrations of structures of circular cross-section-part 2: development of a mathematical model for full-scale application [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1983, 12(1): 75-97.

[11] CAI Y, CHEN S S. Dynamic response of a stack-cable system subjected to vortex-induced vibration [J]. Journal of Sound and Vibration, 1996,196(3): 337-349.

[12] FACHINETTI M L, DE LANGRE E, BIOLLEY F. Vortex shedding modeling using diffusive van der Pol oscillators [J]. Comptes Rendus Mécanique, 2002,330(7): 451-456.

[13] MATHELIN L, DE LANGRE E. Vortex-induced vibrations and waves under shear flow with a wake oscillator model [J]. European Journal of Mechanics B/Fluids, 2005, 24(4): 478-490.

[14] 陈伟民, 张立武, 李敏. 采用改进尾流振子模型的柔性海洋立管的涡激振动响应分析 [J]. 工程力学, 2010, 27(5): 240-246.

CHEN Weimin, ZHANG Liwu, LI Min. Prediction of vortex-induced vibration of flexible riser using improved wake-oscillator model [J]. Engineering Mechanics, 2010, 27(5): 240-246.

[15] FARSHIDIANFAR A, ZANGANEH H. A modified wake oscillator model for vortex-induced vibration of circular cylinders for a wide range of mass-damping ratio [J]. Journal of Fluids and Structures, 2010, 26(3): 430-441.

[16] VIOLETTE R, DE LANGRE E, SZYDLOWSKI J. A linear stability approach to vortex-induced vibrations and waves [J]. Journal of Fluids and Structures, 2010, 26(3): 442-466.

[17] 高云, 宗智, 于馨. 均匀来流中Spar平台涡激运动响应研究[J]. 中国科学:物理学 力学 天文学, 2011, 41(2): 132-139.

GAO Yun, ZONG Zhi, YU Xin. Response analysis of vortex induced Spar motions in uniform currents [J]. Scientia Sinica: Physics, Mechanics, Astronomy, 2011, 41(2): 132-139.

[18] SRINIL N. Analysis and prediction of vortex-induced vibrations of variable-tension vertical risers in linearly sheared currents [J]. Applied Ocean Research, 2011, 33(1): 41-53.

[19] 郑中钦, 陈伟民. 结构与尾流非线性耦合涡激振动预测模型 [J]. 海洋工程, 2012, 30(4): 37-54.

ZHENG Zhongqin, CHEN Weimin. Prediction of vortex-induced vibration of cylinder based on the nonlinear coupling of structure and wake oscillator [J]. The Ocean Engineering, 2012, 30(4): 37-54.

[20] GROUTHIER C, MICHELIN S, BOURGUET R, et al. On the efficiency of energy harvesting using vortex-induced vibrations of cables [J]. Journal of Fluids and Structures, 2014, 49(8): 427-440.

[21] XU K, GE Y, ZHANG D. Wake oscillator model for assessment of vortex-induced vibration of flexible structures under wind action [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 136: 192-200.

[22] FACCHINETTI M L, DE LANGRE E, BIOLLEY F. Coupling of structure and wake oscillators in vortex-induced vibrations [J]. Journal of Fluids and Structures, 2004, 19(2): 123-140.

[23] NORBERG C. Fluctuating lift on a circular cylinder: review and new measurements [J]. Journal of Fluids and Structures, 2003, 17(1): 57-96.

[24] FACCHINETTI M L, DE LANGRE E, BIOLLEY F. Vortex-induced travelling waves along a cable [J]. European Journal of Mechanics B-Fluids, 2004, 23(1): 199-208.

[25] DE LANGRE E. Frequency lock-in is caused by coupled-mode flutter [J]. Journal of Fluids and Structures, 2006, 22(6): 783-791.

[26] VIOLETTE R, DE LANGRE E, SZYDLOWSKI J. Computation of vortex-induced vibrations of long structures using a wake oscillator model: comparison with DNS and experiments [J]. Computers and Structures, 2007, 85(11): 1134-1141.

[27] NEWMAN D J, KARNIADAKIS G E. A direct numerical simulation study of flow past a freely vibrating cable [J]. Journal of Fluid Mechanics, 1997, 344: 95-136.

Numericalstudyofresponseperformanceofvortex-inducedvibrationonaflexiblecylinderusingamodifiedwakeoscillatormodel

GAO Yun1,2, TAN Nuan1, XIONG Youming1, ZOU Li3, ZONG Zhi3

(1. State Key Laboratory of Oil and Gas Reservoir Geology and Exploration, Southwest Petroleum University, Chengdu 610500, China; 2. School of Mechanical Engineering, The University of Tokyo, Tokyo 113-8656, Japan; 3. School of Naval Architecture, Dalian University of Technology, Dalian 116024, China)

Numerical study was conducted for the response performance of VIV of a flexible cylinder based on a modified wake oscillator model. The structure oscillator model of a flexible cylinder and wake oscillator model were established, and then the two models were coupled. Parameters analyses of non-dimensional displacement, phase angle, frequency ratio and displacement fluctuation characteristics were executed by changing non-dimensional tension, aspect ratio and mass ratio. The analysis results indicate that the VIV response of a flexible cylinder has an obvious travelling wave behavior. The propagation speed increases as non-dimensional tension increases and aspect ratio decreases, respectively. The phase angle has a sudden transition with increased non-dimensional tension and aspect ratio. The sudden transition appears at the point when the vibrating frequency passes the natural frequency.

flexible cylinder; wake oscillator model; numerical study; travelling wave; phase angle

国家自然科学基金资助项目(51609206；51522902；51379033)；国家留学基金资助项目(201608515007)

2016-06-08 修改稿收到日期： 2016-08-30

高云 男, 讲师, 硕士生导师, 1985年生

E-mail: dutgaoyun@163.com

O357

A

10.13465/j.cnki.jvs.2017.22.014