基于循环相关和LPSO算法的自适应MCKD方法的滚动轴承早期故障特征提取

陈昆弘， 刘小峰

(重庆大学 机械传动国家重点实验室，重庆 400044)

基于循环相关和LPSO算法的自适应MCKD方法的滚动轴承早期故障特征提取

陈昆弘， 刘小峰

(重庆大学 机械传动国家重点实验室，重庆 400044)

针对强噪声情况下滚动轴承早期故障信号特征难以提取的问题，提出了MCKD与对称差分能量算子解调的特征提取方法。MCKD算法进行滤波时，滤波器长度L和故障周期T对滤波效果的影响至关重要，因此提出基于循环相关和LPSO算法结合的自适应的MCKD算法，自动搜寻MCKD算法所需最优参数；原信号经滤波后，故障特征被明显突出，为了剔除剩余噪声，对滤波后信号进一步做对称差分能量算子解调，剔除剩余噪声同时获得解调谱，进而提取滚动轴承的早期故障。实验分析验证了该方法的有效性。

循环相关； 局部粒子群优化； 最大相关峭度解卷积； 对称能量算子解调； 早期故障； 特征提取

滚动轴承出现早期局部故障时，故障产生的冲击成分一般十分微弱，往往会被强大的背景噪声淹没而无法提取。针对该问题，不少学者进行了深入研究。莫代一等[1]提出一种基于双重Q因子的故障诊断方法，可将轴承早期故障信号分解成高共振和低共振两个分量，对低共振分量进行分析即可提取出轴承故障特征信息，但该方法的参数过多，如果任一参数设定不合理都会对最终结果产生不利影响；曾庆虎等[2]利用小波相关滤波的降噪特性，将相关滤波降噪与包络谱相结合，提出了基于小波相关滤波包络分析的轴承早期微弱故障特征提取，诊断效果明显，然而该方法中小波基函数的选择缺乏自适应性，选取不同的小波基函数时，诊断结果差异较大；王宏超等[3]将最小熵卷积(Minimum Entropy Deconvolution, MED)用于早期轴承信号的降噪，取得了较好的效果。McDonald等[4]对MED进行了改进，提出了最大相关峭度解卷积(Maximum Correlated Kurtosis Deconvolution, MCKD)方法，以相关峭度为评价指标，充分考虑了信号所含冲击成分的周期特性，通过迭代过程实现解卷积运算，突出信号中被强烈噪声所掩盖的连续脉冲，并用于齿轮故障诊断，取得了良好的效果。

钟先友等[5-6]研究发现，采用MCKD对滚动轴承早期振动信号进行降噪，也取得了良好的结果，但有限冲击响应滤波器长度和信号周期这两个参数决定了滤波效果，实际过程中，往往采用试验的方法确定，浪费时间，故需要采用一种自适应的方法，使得MCKD方法取得较优效果。

本文提出将LPSO(Local Particle Swarm Optimization)算法和循环相关结合，对MCKD的影响参数进行寻优，实现自动寻找最优参数的自适应MCKD算法，并结合对称能量算子解调[7]，得到滤波后信号解调谱，分析故障特征。实例分析表明，该方法可有效提取滚动轴承的早期故障特征。

1 MCKD原理

为了提取周期故障信号，MCKD通过选定一个有限冲击滤波器f使周期已知信号滤波后的相关峭度最大，从而使得信号中的冲击成分最突出。相关峭度的定义为

(1)

式中：yn为周期信号；T为信号的周期；f为滤波器向量；L为滤波器长度；M为位移数，增加位移数能增加算法的周期序列脉冲数。M一般取值为1～7，当M的取值大于7时，会使计算超出浮点数范围，因此本文选取的M值为7。

为了选取一个最优的滤波器f，使得CKM(T)最大，根据函数求极值，即令

(2)

算得的结果及其矩阵表示为

(3)

其中，

r=[0T, 2T, …,mT],

在MCKD算法中，滤波器长度L和故障信号周期T两个因素决定着滤波器滤波效果。本文提出了改进的局部PSO(Particle Swarm Optimization)算法和循环相关结合的方法，自动获得L和T两个参数的最优解，使得MCKD能够对周期未知信号进行滤波，扩大了MCKD滤波算法的适用范围。

2 改进的LPSO算法

PSO算法是一种粒子群优化算法，具有较好的全局寻优能力，假设在D维空间中有M个粒子，即其组成的粒子空间X=(X1,X2, …,XM)，每个粒子是一个D维向量，其第i个粒子的向量为Xi=(xi1,xi2, …,xiD)，代表第i个粒子在D维搜索空间中的位置， 同时，第i个粒子的速度为Vi=(vi1,vi2, …,vin)， 其个体历史最优解Pi=(pi1,pi2, …,pin)，整个空间的全局最优解为G=(g1,g2, …,gn)，其粒子随着迭代的进行，速度和位置变化更新公式为

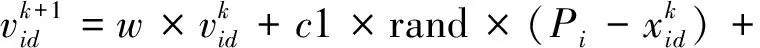
(4)

(5)

式中：w为惯性因子；i=1,2,…,M；d=1,2,…,D；k为当前的迭代次数；c1，c2为粒子的学习因子。rand是介于[0,1]的随机数。

以上就是标准PSO算法。然而，标准PSO算法存在易陷入局部最优的缺点。故本文是用改进后的局部PSO算法(LPSO)，改进了速度更新公式，将粒子群的全局历史最优解g替换为粒子的邻域内粒子的最优解pnext，使得粒子群速度更新不再依赖全局最优，不易陷入局部最优解。改进后的速度更新公式为

(6)

式中，pi next为第i个粒子邻域内粒子的最优解。

[8]发现，为使粒子群算法中的速度变化取得更好的收敛效果，从而得到更精确的结果，惯性因子w按照凹函数变化时优于线性变化，线性变化优于常量，因此本文中w采用凹函数随迭代次数而变化，公式如下

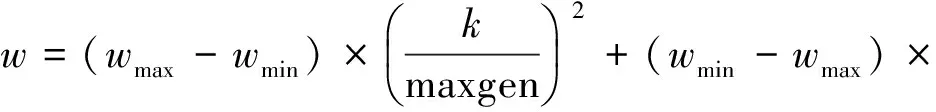
(7)

式中：wmax为w的最大值；wmin为w的最小值；k为粒子群此次迭代次数； maxgen为PSO算法的总迭代次数。

在标准粒子群算法中，学习因子c1、c2一般是恒定的常值，但是依据实验表明，随着迭代而变化的学习因子可以获得更好的收敛效果，即在粒子进化初期，使粒子能仔细的在自己的邻域内搜索，防止粒子较快地收敛于局部最优解；而在进化后期，应使粒子群更快、更准确地收敛于全局最优解[9]。即在初期使c1的值较大，而在后期使c2的值随着迭代次数增大。故改进的学习因子公式为

(8)

c2=4-c1

(9)

使用粒子群进行寻优解时，需要选取一个适应度函数来衡量寻优效果。每当粒子更新自己的位置时，根据适应度函数，计算一次适应度的值，再比较选出最优解。依据钟先友等的研究，结合实际中的实验表明，信噪比在衡量MCKD滤波效果方面，比各种熵值衡量效果较优，故本文选取信噪比作为粒子群的适应度函数，用于评判粒子在MCKD滤波效果方面的优劣。即对MCKD滤波后信号取包络，计算功率谱，再计算信噪比Rsnr

(10)

(11)

式中：S(f0)为滤波后信号的功率谱；N(f0)为原信号的功率谱；f0为滤波后信号在故障频率附近的平均值。信噪比越大，表明滤波效果越好。

在本文处理信号时，因为未提前预知信号故障频率f0，故需要对信号进行预处理。本文提出，通过循环相关算法，对信号频率进行预筛选，得到可能的信号频率f=[f1f2f3…]，再通过LPSO算法得到精确值。

3 循环相关

MCKD滤波器中，需要确定[L,T]两个变量，但是在测试中发现局部PSO算法在处理多变量多峰函数时，即含噪声信号时，依然得不到足够精确的解。故本文在局部PSO算法前，加入循环相关算法，在信号进入局部PSO算法处理前，利用循环相关，对信号的周期T做一轮筛选，使得局部PSO算法对变量T的搜索范围极大的减小，提高整个算法的精确程度。循环相关分析中，所提取的信号周期定义为循环周期Tα，频率称之为循环频率α，全部循环频率的集合定义为循环频率域[10]。

定义信号x(t)的自相关函数为

(12)

式中：*为共轭运算；τ为时间延迟变量。

当x(t)为二阶循环平稳信号时，Rx(t,τ)随时间变化呈现出周期特征， 即Rx(t,τ)=Rx(t+Tα,τ)，Tα=1/α表示循环周期。因此，二阶循环平稳信号的自相关函数Rx(t,τ)可以用傅里叶级数展开为

(13)

(14)

循环自相关函数能够将调幅信号的调制频率解调到循环频率低频带上，实现与载波频率的分离。根据循环相关结果图和对应切片图，对信号周期进行初步筛选，得到信号频率f=[f1f2f3…]，进而得到对应的周期T=[T1T2T3…]，在程序中，所需T的计算方法为Tn=fs/fn。

此时，再初始化变量L，将得到的多个周期序列T与变量L组成一个二维变量[L,T]，然后由LPSO自动搜寻最优解。

4 对称差分能量算子解调

能量算子解调相对于FFT(Fast Fourier Transform)解调而言，对噪声不敏感，能较好的突出信号特征部分，但是基本的能量算子解调算法在端点处以及突变点处仍比较敏感，为了尽量减少这些因素对信号解调的影响，故本文选取改进后的对称差分能量算子解调对滤波后信号进行处理。

离散信号的瞬时幅值—频率表示为

x(n)=a(n) cos(φ(n) )=
a(n) cos(ω(n)+θ)

(15)

对x(n)进行能量算子计算得

φx(n)=x2(n)-x(n-1)x(n+1)

(16)

又由于φ(a(n) )≈0，φ″≈0，式(16)简化为

φ(x(n) )≈a2(n) sin2(ω(n))

(17)

对称差分能量算子解调对能量算子中的差分序列进行了改进。首先，对x(n)的差分序列定义为

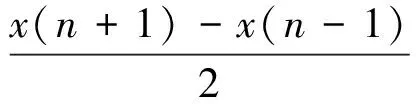
(18)

y(n)的差分序列定义为

(19)

得到改进的算子

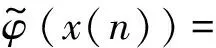
(20)

使用传递函数求解，得到能量算子的幅、频估计值为

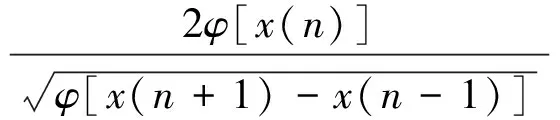
(21)

(22)

5 故障分析

在实际分析中，选择合适[L,T]参数，突出被噪声淹没的特征成分，是利用MCKD进行滚动轴承早期故障特征分析的关键。利用循环相关对T参数进行第一轮筛选后，再利用改进LPSO对[L,T]参数进行第二轮筛选，既避免了人为设定的主观性，又提高了对[L,T]两参数选择的准确性。在信号经MCKD滤波后，信噪比会显著提高，但仍存在部分噪声。利用对称差分能量算子解调对噪声的不敏感特性，可有效地剔除噪声并得到解调谱。具体故障分析步骤如下：

步骤1利用循环相关筛选的多个周期合成的周期数组T。

步骤2设定LPSO算法的粒子群种群大小M和迭代次数N，设置惯性因子的最大值wmax及最小值wmin，初始化L，并与由步骤1得到的T组成二维变量数组[L,T]。

步骤3将[L,T]和信号输入改进LPSO中，利用改进LPSO对MCKD的两个影响参数进行寻优，得到最优解[L0,T0]。

步骤4根据[L0,T0]，输入MCKD滤波器对信号进行滤波，得到滤波后信号。

步骤5对滤波后信号根据对称差分能量算子解调，得到信号的解调谱。

步骤6根据解调谱分析信号，判断信号故障类型。

在本文中，默认粒子群种群大小M=30，迭代次数N=20，wmax=0.9，wmin=0.4。

6 仿真信号分析

滚动轴承的故障大部分都是周期性冲击信号，故仿真信号采用周期冲击信号，其模拟表达式为

x(t)=5×e-c(t-kT)×sin[2πf(t-kT) ]×
U(t-kT)+n(t)k=1,2,3,…

(23)

式中：f为信号的固有频率，设为3 kHz；T为故障冲击周期，设为1/100； 阻尼系数c=0.1，U(t-kT)为单位阶跃函数；n(t)为噪声。本次模拟中，采样频率为20 kHz。噪声为高斯白噪声，信噪比为-5，其时域波形和频谱如图1所示。

对信号进行Hilbert包络解调得到波形，如图2所示。由图2可知，故障频率可以识别，但是有太多的杂频，不易快速辨认。

图1 复合信号的时域波形及频谱图Fig.1 The time domain and frequency domain of composite signal

图2 复合信号的Hilbert包络解调谱Fig.2 The Hilbert envelop spectrum of composite signal

对模拟使用基本LPSO算法和对称能量算子解调对模拟信号进行处理，设置算法中惯性因子ω=0.7，c1=1.49,c2=1.49，变量为[L,T]，当迭代至第18次时，得到最优解 [L0,T0]=[131,500]，再将最优解代入MCKD算法，得到滤波后信号，再对滤波后信号用对称差分能量算子解调，处理结果如图3所示。由图3可知，虽然可以辨认故障频率，但杂频太多，效果并不明显。

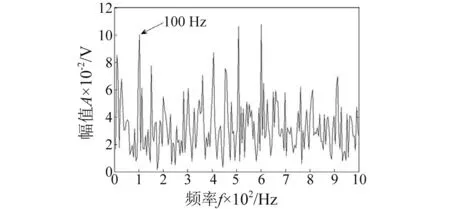
图3 信号进行LPSO和对称能量算子解调结果Fig.3 The result of LPSO and demodulation

利用循环相关对模拟信号进行筛选，得到循环相关结果及τ=1时切片图，如图4所示。由于滚动轴承故障频率在低频段，故只需截取0～500 Hz频带进行筛选，由图明显可知，可选100 Hz及其倍频程为所需频率，根据公式Tn=fs/fn得到筛选后多个周期，序列T=[200,100,67,50]，初始化变量L，组合成所需寻优组合[L,T]。将变量[L,T]和模拟信号输入改进LPSO算法中，自动对[L,T]进行筛选，在第6次迭代时，即当L=343，T=200时，得到最优解，将最优解[L0,T0]=[343,200]输入MCKD方法进行滤波，得到滤波后信号如图5所示。再将滤波后信号用对称差分能量算子解调，得到解调谱，如图6所示。

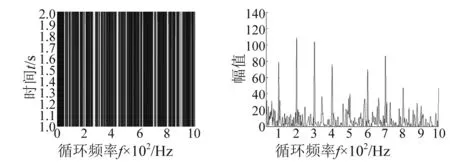
(a) 循环相关结果 (b) τ=1时切片图图4 循环相关处理结果Fig.4 The result of cyclic correlation

图5 滤波后信号Fig.5 The signal after filtering

图6 复合信号对称差分能量算子解调谱Fig.6 The symmetrical differencing energy operator demodulation spectrum of composite signal

由图6可知，信号的故障频率为100 Hz及其倍频程，如图中f及其倍频程标示，与预设值相符，且其他频带对故障的识别无影响。表明利用局部PSO算法和循环均值相结合的自适应MCKD滤波器能对模拟信号有较好的滤波效果。

7 实验验证

本文采用西储大学公开的轴承故障数据进行实验验证。西储大学在实验中采用一台2马力的电机进行驱动，加速度传感器采集信号，信号通过16通道的DAT记录器记录。本文使用采样率12 kHz条件下的107 mat文件中的驱动端数据进行验证，并在实验前，加上-1 dB的高斯白噪声。其中主要参数如下：故障深度0.178 mm英寸，载荷为1.491 4 kW，实际转速1 772 r/min，内圈故障。取2 048个点进行分析，其时域波形及频谱如图7所示。

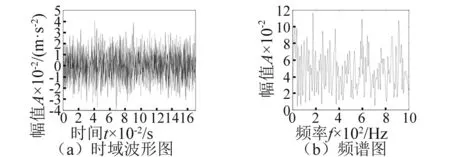
图7 信号时域波形图及其频谱Fig.7 The time domain and frequency domain of signal

对信号进行Hilbert包络解调，得到波形图如图8所示。由图可知，Hilbert包络解调已经不能准确识别信号成分。

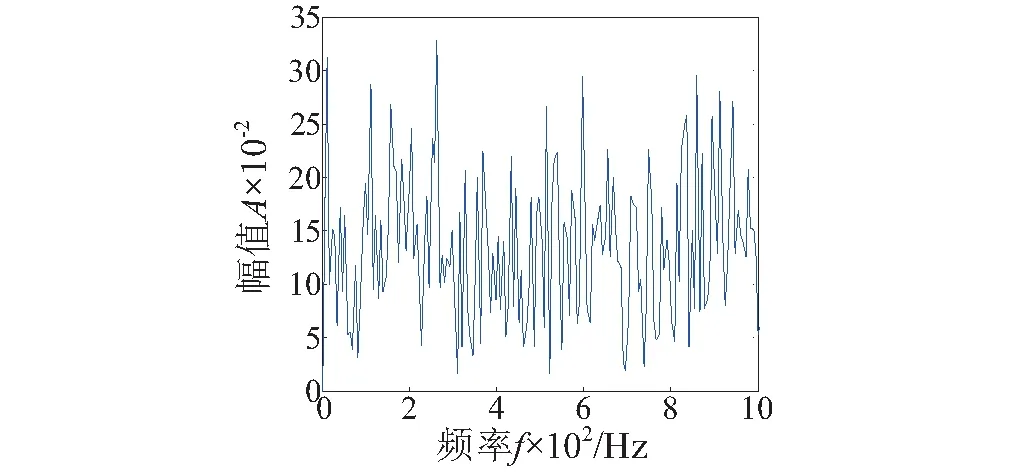
图8 Hilbert包络处理结果Fig.8 The Hilbert envelop of signal

对信号以[L,T]为未知量，使用基本LPSO进行筛选，再对滤波后信号进行对称差分能量算子解调，其中设置算法中惯性因子ω=0.7，c1=1.49,c2=1.49，在迭代至第13次时，得到最优解[L0,T0]=[10,500]，将最优解代入MCKD方法，得到滤波后信号，再对滤波后信号进行对称能量算子解调，解调结果如图9所示。由图9可知，几乎无法准确识别故障特征。

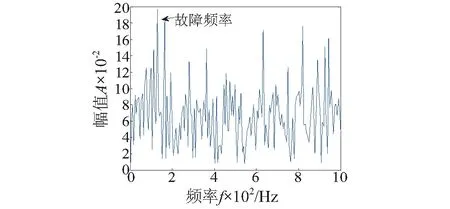
图9 信号进行LPSO和能量算子解调结果Fig.9 The result of LPSO and symmetrical differencing energy operator demodulation

对信号做循环相关，并对得到频率通过切片进行筛选，循环相关结果在τ=1时切片图，如图10所示。因大部分的滚动轴承故障都集中在低频段，故只需截取0～500 Hz范围选取频率，取幅值大于0～500 Hz幅值均值点对应频率作为筛选频率，将筛选后的频率求得对应T=[187,145,86,76,40,34,24]，初始化变量L，组成二维变量矩阵[L,T]，与原始信号一同导入改进LPSO算法中自动寻优，在迭代至18次时，得到最优解T=76,L=496,将最优解[L0,T0]=[496,76]输入MCKD方法，得到滤波后信号后，如图11所示。再对信号进行对称差分能量算子解调，得到解调谱如图12所示。

由图12可知，故障信号为158.2 Hz及其倍频程，如图中f及其倍频程所标示，与理论计算结果趋于一致，且其余信息对故障识别几乎没有影响，效果较优。说明本文所述方法能较好地对早期滚动轴承故障信号进行处理。

图10 循环相关切片结果Fig.10 The slice of cyclic correlation

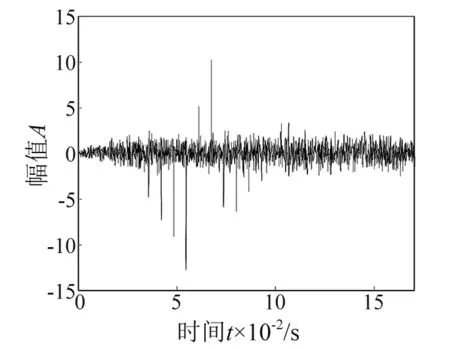
图11 滤波后信号Fig.11 The signal after filtering

图12 故障信号对称差分能量算子解调谱Fig.12 The symmetrical differencing energy operator demodulation spectrum of signal

8 结 论

通过实例验证，表明采用循环相关和LPSO结合的自适应MCKD滤波、对称差分能量算子解调的方法在进行滚动轴承的早期故障诊断是可行的。本文得到的主要结论有：

(1) 自适应的MCKD滤波器滤波效果相对于简单的Hilbert包络解调效果好。

(2) 与未用循环相关做第一次筛选，粒子群参数未改进的LPSO算法和能量算子解调的特征提取方法相比，有明显地优化。

(3) 通过仿真和实验验证表明，本文提出的滤波算法在处理滚动轴承早期故障方面具有较好的效果，具有一定的工程应用价值。

参 考 文 献

[ 1 ] 莫代一，崔玲丽，王婧.基于双重因子的稀疏分解法在滚动轴承早期故障诊断中的应用[J].机械工程学报, 2013, 49(9): 37-41.

MO Daiyi, CUI Lingli, WANG Jing. Sparse signal decomposition method based on the dual Q-factor and its application to rolling bearing early fault diagnosis [J]. Journal of Mechanical Engineering, 2013, 49(9): 37-41.

[ 2 ] 曾庆虎，邱静，刘冠军，等.基于小波相关滤波-包络分析的早期故障特征提取方法[J].仪器仪表学报, 2008, 29(4): 729-933.

ZENG Qinghu, QIU Jing, LIU Guanjun, et al. Approach to extraction of incipient fault features based on wavelet correlation filter and envelope analysis [J]. Chinese Journal of Scientific Instrument, 2008, 29(4): 729-933.

[ 3 ] 王宏超，陈进，董广明.基于最小熵解卷积与稀疏分解的滚动轴承微弱故障特征提取[J].机械工程学报, 2013, 49(1): 88-94.

WANG Hongchao, CHEN Jin, DONG Guangming. Fault diagnosis method for rolling bearing’s weak fault based on minimum entropy deconvolution and sparse decomposition [J]. Chinese Journal of Mechanical Engineering, 2013, 49(1): 88-94.

[ 4 ] MCDONALD G L, ZHAO Q，ZUO M J. Maximum correlated Kurtosis de-convolution and application on gear tooth chip fault detection [J]. Mechanical Systems and Signal Processing, 2012, 33(1): 237-255.

[ 5 ] 钟先友，赵春华，陈保家，等.基于形态自相关和时频切片分析的轴承故障诊断方法[J].振动与冲击, 2014, 33(4): 11-16.

ZHONG Xianyou, ZHAO Chunhua, CHEN Baojia, et al. Bearing fault diagnosis method based on morphological filtering, time-delayed autocorrelation and time-frequency slice analysis [J]. Journal of Vibration and Shock, 2014, 33(4): 11-16.

[ 6 ] 唐贵基，王晓龙．自适应最大相关峭度解卷积方法及其在轴承早期故障诊断中的应用[J]．中国电机工程学报， 2015，35(6): 1436-1444.

TANG Guiji, WANG Xiaolong. Adaptive maximum correlated kurtosis deconvolution method and its application on incipient fault diagnosis of bearing [J]. Proceedings of the CSEE, 2015, 35(6): 1436-1444.

[ 7 ] 李姗姗.基于 LMD 时频分析的旋转机械故障特征提取方法研究[D].秦皇岛:燕山大学, 2013.

[ 8 ] 陈贵敏，贾建援，韩琪.粒子群优化算法的惯性权值递减策略研究[J].西安交通大学学报, 2006, 40(1): 53-57.

CHEN Guimin, JIA Jianyuan, HAN Qi. Study on the strategy of decreasing inertia weight in particle swarm optimization algorithm [J]. Journal of Xi’an Jiaotong University, 2006, 40(1): 53-57.

[ 9 ] 刘国安.粒子群算法改进研究及其在图像检索中的应用[D].哈尔滨:哈尔滨工程大学,2008.

[10] 彭畅.旋转机械轴承振动信号分析方法研究[D].重庆:重庆大学, 2014.

[11] ELEGBEDE C. Structural reliability assessment based on particles swarm optimization [J].Structural Safety, 2005, 27(10): 171-186.

[12] 王天金，冯志鹏，郝如江，等.基于Teager能量算子的滚动轴承故障诊断研究[J].振动与冲击, 2012, 31(2): 1-5.

WANG Tianjin, FENG Zhipeng, HAO Rujiang, et al. Fault diagnosis of rolling element bearings based on Teager energy operator [J].Journal of Vibration and Shock, 2012, 31(2): 1-5.

[13] 周敏，李太勇.粒子群优化算法中的惯性权值非线性调整策略[J].计算机工程, 2011, 37(5): 204-206.

ZHOU Min, LI Taiyong. Nonlinear adjustment at strategy of inertia weight in particle swarm optimization algorithm [J]. Computer Engineering, 2011, 37(5): 204-206.

[14] 何正嘉，訾艳阳，张西宁.现代信号处理及工程应用[M].西安：西安交通大学出版社, 2007.

[15] 周福昌.基于循环平稳信号处理的滚动轴承故障诊断方法研究[D].上海：上海交通大学，2006.

Incipientfaultdiagnosisofrollingelementbearingbasedonadaptivemaximumcorrelatedkurtosisdeconvolution

CHEN Kunhong, LIU Xiaofeng

(The State Key Laboratory of Mechanical Transmissions, Chongqing University, Chongqing 400044, China)

Aiming at the problem that the feature of incipient fault of rolling element bearing is difficult to be extracted under strong noise background, a fault diagnosis method based on MCKD and symmetrical differencing energy operator demodulation was proposed. The filter sizeLand the period of interesting signalTplay an important role in MCKD filtering. An adaptive MCKD filter based on cyclic correlation and LPSO was proposed, which could search for the best parameters automatically. The feature after filtering was outstanding, but some residual noise was still remained. To reduce the residual noise and get the demodulation spectrum, symmetrical differencing energy operator demodulation was applied after filtering. The result of incipient fault diagnosis of rolling element bearing shows that the method is effective.

cyclic correlation; local particle swarm optimization(LPSO); maximum correlated kurtosis deconvolution (MCKD); symmetrical differencing energy operator demodulation; incipient fault; feature extraction

国家自然科学基金项目(51475052)；中央高校基本科研业务费(106112016CDJZR115502)

2016-05-24 修改稿收到日期： 2016-09-06

陈昆弘 男，硕士，1991年生

刘小峰 女，博士，教授，博士生导师，1980年生

TH133.3; TH17

A

10.13465/j.cnki.jvs.2017.22.013