微尺度悬臂管的空间弯曲振动-非线性运动方程及尺度效应

郭 勇， 谢建华

(西南交通大学 力学与工程学院，成都 610031)

微尺度悬臂管的空间弯曲振动-非线性运动方程及尺度效应

郭 勇， 谢建华

(西南交通大学 力学与工程学院，成都 610031)

具有圆环形横截面的微尺度悬臂输液管可以同等地向空间各方向产生弯曲振动。按照欧拉-伯努利梁理论，在分析管道上点的位移及相关几何关系的基础上，考虑Lagrange应变张量所给出的几何非线性，基于修正的偶应力理论计算了管的应变能，运用Hamilton原理建立了微尺度悬臂输液管的空间弯曲振动的非线性动力学方程。研究了无量纲材料长度尺寸参数对系统动力学性质的影响，结果表明，尺度效应增大管道的临界流速，并使得稳定的平面周期运动(空间周期运动)在整个质量比区间上占的比例越大(小)。

微尺度悬臂管；空间弯曲振动；偶应力理论；Lagrange应变张量；周期运动

输液管道是一种重要的工程结构，在实际应用中，管道横截面通常被设计成圆环形，从而可以同等地向空间各方向弯曲。在宏观管研究方面，Lundgren等[1]用力平衡法推导了输液管道的空间振动方程。Bajaj等[2]研究悬臂管的空间振动，运用严格的方法将无穷维系统降阶为限制在不变流形上的三个方程，在此基础上论述了管道平面周期运动、空间周期运动及环面运动的存在性、稳定性。Wadham-Gagnon等的工作推进了悬臂管空间非线性振动问题的研究。Wadham-Gagnon等[3]用Hamilton原理推导了具有弹簧约束和终端质量的悬臂输液管的空间弯曲振动方程。Païdoussis等研究了中间支承弹簧对悬臂管的三维运动的影响。Modarres-Sadeghi等研究了自由端附有质量块的悬臂管的空间动力学行为。文献[4-5]还讨论了作伽辽金离散时所取模态数对问题结果的影响。Ghayesh等[6]首次考虑支承弹簧和末端质量块同时存在时悬臂管的空间运动。Chang等[7]研究了具有末端附加质量的悬臂管的受迫振动。

随着科学技术的发展，管道的特征尺寸可以设计得越来越小，在文献[8]中，圆型微管的内径已达1～100 μm的数量级。微尺度管道广泛应用于微机电力学系统以及微流体的传输，例如微流管已应用于谐振器的设计及药物的注射[9-10]，微流管喷头已应用于微小平面的书写及打印等等[11-12]。为给实际应用提供理论基础，有必要对微尺度流管的动力特性及稳定性进行深入的研究。Fleck等[13-15]的工作表明，微结构具有尺度依赖行为。因此，不能直接对微尺度管应用宏观管理论，需要借助非经典的连续介质力学理论对其加以描述。实验观测表明，对于微结构的扭转、弯曲等，由Yang等[16]所修正的偶应力理论能够成功地估计其尺度效应。基于该理论，微梁的自由振动[17]、强迫振动[18]、屈曲[19]、参数振动[20]等相继得到研究。在微尺度流管研究方面，Wang等[21-22]分别在输液管的欧拉梁模型和Timoshenko梁模型假设下建立微管的线性振动方程，考察了不同微尺度情形下流速对管道固有频率的影响。文献[23]研究微管的空间弯曲振动的线性方程，不仅考虑了管材料的微尺度效应，还引入了管内流体的微尺度因素。Yang等[24]考虑轴向拉伸所导致的几何非线性，基于修正的偶应力理论研究了微管的平面振动。Hosseini等[25]考虑悬臂微管平面振动的稳定性问题，研究了微尺度效应对系统频率、临界流速的影响，发现相同条件下，微管较之于宏观管具有更大的频率及更高的临界流速。Bahaadini等[26]进一步研究了耗散等因素对科学仪黏弹性碳纳米悬臂管稳定性的影响。Tang等[27]研究了两端固支曲管的空间非线性振动。

从已有文献可知，在微尺度输液管的动力学建模方面，平面或者空间振动的非线性方程均是针对两端支撑管建立的，对悬臂管的大振幅空间弯曲振动问题，目前似还没有相应的文献可以参考，因此在非线性建模方面的工作有待完善，进一步地，尺度效应对系统动力学性质的影响有待考察。当考虑微尺度效应的时候，微元体的应变能不能明显地表示为管的形心线(管横截面的形心连线)曲率的函数，因此本文从应变能的基本表达式出发，结合运动的几何分析，运用Hamilton原理建立系统的非线性动力学方程；以此为基础，研究了尺度效应对管道振动特性的影响。

1 力学模型、位移场及相关几何分析

如图1(a)所示，长为L的微尺度悬臂输液管，横截面积为Ap，抗弯刚度为EI，单位长度的质量为m，其输送的流体单位长度的质量为M，流速V相对管的形心线为常数。管的横截面是具有O(2)对称性的圆环(见图1(b))。

以管道未变形时的形心线为x轴，悬臂端面为yz平面建立参考系oxyz(见图1(c))，管道作一般的空间弯曲振动(见图1(d))。取另一个坐标系OXYZ与管道固结，作为管道上物质点的拉格朗日描述，该系在管未变形时与oxyz重合。X的值等于管道横截面形心离原点的弧长s，因此，为了突出物理意义，以下用(s,Y,Z)代替(X,Y,Z)表示管道上的物质点的坐标。

图1 力学模型Fig. 1 The mechanical model

分析管道上点的位移及相关的几何关系，借此导出它的应变能。本文考虑细长管，根据欧拉-贝努利梁假设，由j′k′(见图1(d))确定的圆截面视为刚性的，即在运动过程中不发生变形。从而管道上某点在任一瞬时的位移包括：其所在的横截面随圆心的平移部分及该面绕圆心的转动部分。平移部分容易分析，也就是随形心线的运动(见图2(a)中点圈到短划线圈的平移)。下面分析转动部分。我们知道，圆心固定的刚性圆盘在空间的位置由两个方面确定：过圆心的法线及绕法线的转动(见图2(b))。因此，管道上任一横截面在平移之后的转动部分可以分解为：

(1) 平移后的构形绕圆心(具体为绕图2(a)中的ω轴)旋转至与瞬时构形平行(见图2(c)中的短划线圈旋转到实线圈)。

(2) 图2(c)中的实线圈绕过圆心的法线(如图2(d)所示的τ轴)旋转，直到与瞬时构形(粗实线圈)重合。

设管道形心线上一点(s, 0, 0)在t时刻的位置为

r=r(s,t)=(s+u,v,w)

(1)

由欧拉-贝努利梁假设，横截面在运动的过程中始终垂直于管道形心线的切线，即切线与τ轴重合。刚体绕点的有限转动可以通过刚体绕某条过该点的轴的一次转动实现，从而转动(i)的有限转角方向为

(2a)

单位化以后得

图2 横截面的运动Fig. 2 The motions of a cross section

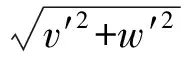
(2b)

转角大小|ω|为转动前后横截面各自的法线方向i与τ的夹角(见图3)，满足关系

图3 转角大小|ω|的几何关系Fig. 3 The geometrical relation for the rotation

(3)

因为没有初始外力矩，绕τ轴的转动为零。

虽然有限转动可以用一个有大小、有方向的量描述，但是其不满足矢量运算，因此不是矢量，即

ω1+ω2≠ω2+ω1

但是转动沿弧长方向的无穷小增量却是一矢量，满足矢量运算平行四边形法则所要求的对易律，即

[ω(s+ds)-ω(s)]

(4)

是一矢量。

由以上转动分析可知转动所导致的截面上点的轴向位移

(5)

至此可以写出位移场，也就是点(s,Y,Z)的位移

(6)

式中，(u,v,w)为形心线上点的位移，见式(1)。

因为没有初始轴力，可认为管的形心线在运动中不发生伸长或压缩，从而式(7)成立

(1+u′)2+v′2+w′2=1

(7)

2 应变能的计算及动能

微尺度结构中微元体的应变能密度表达式和通常弹性力学中给出的不同，其不仅是应变张量的函数，而且还包括曲率张量对能量的贡献项，该部分可由一个材料长度尺寸参数加以刻画。根据文献[16]中的结论，各向同性线弹性材料区域Ω内的应变能可以写成

(8)

式中：σ和ε分别为应力张量和应变张量；m、χ分别为偶应力张量的偏部分和对称曲率张量，其相互间的关系为

σ=λtr(ε)δ+2Gε

(9)

ε=(1/2)[u+(u)T]+(1/2)u·(u)T

(10)

m=2l2/Gχ

(11)

χ=(1/2)[θ+(θ)T]

(12)

式中：λ、G为Lamé常数，其中G也就是通常的剪切模量；δ为单位张量；式(10)为Lagrange应变张量，其非线性部分源于管道的大变形；l为表征微尺度效应的材料长度尺寸参数，取决于材料性质；为拉氏梯度算子；u为位移矢量，其分量见式(1)；θ可通过u的旋度表示为

θ=(1/2)curl(u)

(13)

由不可压缩条件式(7)

(14)

对转角关系式(3)可以进行如下一系列简化

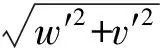
(15)

由式(6)，式(9)～式(13)均可计算出，代入式(8)并利用式(14)、式(15)对其进行整理，得应变能

(16)

式中，dv=dsdYdZ(下文中如没有其它说明，均是如此)。横向振动相对于管的长度来说是小量，不妨设其为O(ε)阶的。几何大变形意味着方程中的非线性项对系统性态会有本质的影响，但是在平衡态附近，低阶的非线性项才起决定性的作用，因此本文中仅保留了三次非线性项。运用哈密顿原理推导振动方程时，求变分的过程会让作用量泛函的次数降低一次，因此在对式(16)的处理中，仅将其保留到四次项，下文关于动能的推导中亦是如此。

在式(16)中，宏观部分的势能为

(17)

利用截面对称性进一步整理，得

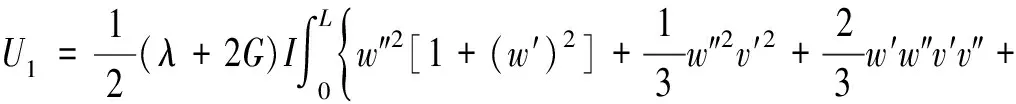
忽略泊松效应，以EI代替上式中的(λ+2G)I，得

(18)

整理微观部分的势能，得

(19)

总的势能为宏观和微观两部分之和

U=U1+U2

(20)

给出动能之前，我们先来研究下面的问题，借此说明下文中宏观部分势能U1的变分与文献[3]中按照弯曲势能公式得到的结果一致。

因式(4)是一矢量，考虑转角沿弧长的变化率，其也是一个矢量

(21)

式(1)对s求导，得

r′=(1+u′)i+v′j+w′k

(22)

上文已经提到，因为没有外加扭矩，截面的相对扭转为零，即转角沿弧长的变化率矢量在形心线切方向上的投影为零，即

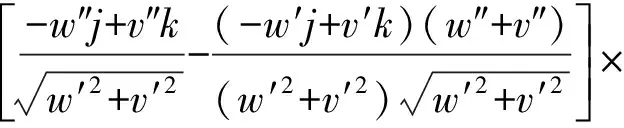
(23)

管道和管中流体的动能分别为

(24a)

(24b)

3 空间弯曲振动方程的推导

将势能式(20)及动能式(24a)、式(24b)代入描述管道振动的哈密顿变分方程[28]

(25)

式中：r见式(1)，下标L表示相应的量在管道自由端s=L处的值，点和撇分别代表∂()/∂t和∂()/∂s。需要指出的是，在下文对变分的计算中，我们可以导出边界条件，并且根据其对式子作了简化。

对势能的宏观部分求变分

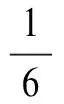
8v′w″w‴+4v′w′w(4))δvdsdt

(26)

根据式(23)可导出

(27)

将式(27)代入式(26)

(28a)

式(28a)与文献[3]中利用公式

计算出的结果一致，其中为管道形心线的曲率。

将式(27)的第一式代入式(19)(势能的微观部分)并对其求变分，得

(28b)

对动能T=Tp+Tf求变分的过程与文献[3]中的相同，经整理，最后得到振动控制方程

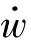
(29a)

(29b)

相应的边界条件为

w(0,t)=w′(0,t)=w″(L,t)=w‴(L,t)=0

(30a)

v(0,t)=v′(0,t)=v″(L,t)=v‴(L,t)=0

(30b)

引入如下无量纲量

得到式(29a)、式(29b)的无量纲形式为

(31a)

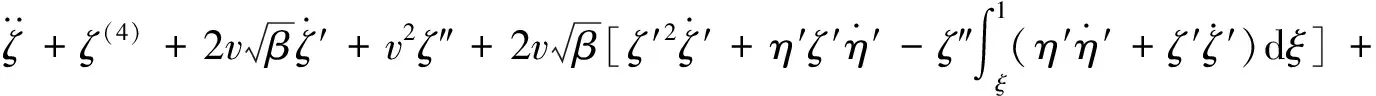
(31b)

相应地，边界条件式(30a)、式(30b)化成

η(0,τ)=η′(0,τ)=η″(1,τ)=η‴(1，τ)=0

(32a)

ζ(0,τ)=ζ′(0,τ)=ζ″(1,τ)=ζ‴(1，τ)=0

(32b)

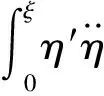
将上面两式代入式(31a)、式(31b)消除其中的非线性惯性项，整理后得到

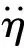
(33a)

(33b)

4 尺度效应的影响

设式(33a)、式(33b)的解为

(34)

式中：r取1～n(n为模态截断数)；φr(ξ)、ψr(ξ)为悬臂梁的特征函数；qr(τ)、pr(τ)为两个横向上相应的广义坐标。根据Galerkin方法，将式(34)代入式(33a)、式(33b)并分别用φr(ξ)、ψr(ξ)乘两边，从0～1积分，可得关于qi,pi的二阶常微分方程组

(35)

其中，

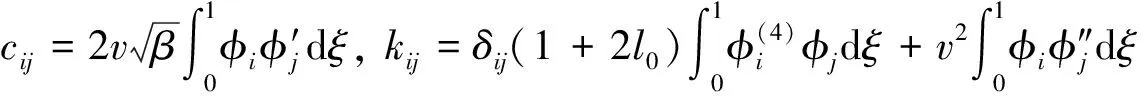
令

(36)

将式(35)化成一阶形式

(37)

根据文献[4]中关于模态截断数的讨论，取n=6。下面给出尺度效应对系统动力学性质的影响规律，包括：①对管道临界流速、临界频率的影响(见图4)；②对管道周期运动类型的影响(见图5)。

从图4可知，无量纲材料长度尺寸参数l0越大，相应的临界流速和临界频率越大，即尺度效应使得管道更稳定。当流速取值在临界流速曲线右边时，管道的初始构形是稳定的；当流速在临界值附近变化时，管道会发生颤振，作平面或者空间的周期运动，以η=0为Poincaré截面，相应的ζ值如图5所示：ζ=0对应系统

作稳定的平面周期运动；ζ≠0对应系统作稳定的空间周期运动。观察图5(a)～图5(d)的变化规律可知，无量纲材料长度尺寸参数l0越大，管道稳定的平面周期运动(空间周期运动)在整个质量比区间上占的比例越大(小)。

图4 临界流速和临界频率Fig. 4 The critical flow velocity and critical frequency

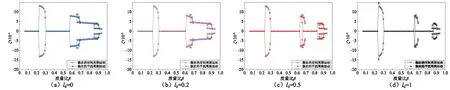
图5 不同尺度管的稳定周期运动的分布Fig. 5 The distribution of stable periodic motion for pipe with different material length scale parameters

5 结 论

(1) 微尺度效应使得微元体的应变能不能明显地表示为管的形心线曲率的函数，本文在分析管道位移场及相关几何关系的基础上，考虑Lagrange应变张量所给出的几何非线性，基于修正的偶应力理论计算了管的应变能，对应变能的退化比较表明其中的宏观部分和已有文献中的结论一致。

(2) 运用Hamilton原理建立了微尺度悬臂管的空间弯曲振动的非线性动力学方程，其中，材料长度尺寸参数对方程的影响得以刻画，其不仅出现在方程的线性项中，影响诸如频率、临界流速等；也出现在方程的非线性项中，影响系统失稳后的分岔性质。

(3) 具体而言：尺度效应增大管道的临界流速和临界频率，即使得管道更加稳定；同时，管道稳定的周期运动类型在整个质量比区间的分布也受尺度效应的影响：无量纲材料长度尺寸参数l0越大，稳定的平面周期运动(空间周期运动)在整个质量比区间上占的比例越大(小)。

[ 1 ] LUNDGREN, SETHNA P R, BAJAJ A K. Stability boundaries for flow induced motions of tubes with an inclined terminal nozzle [J]. Journal of Sound and Vibration, 1979, 64(4): 553-571.

[ 2 ] BAJAJ A K, SETHNA P R. Flow induced bifurcations to three-dimensional oscillatory motions in continuous tubes [J]. SIAM Journal of Applied Mathematics, 1984, 44(2): 270-286.

[ 3 ] WADHAM-GAGNON M, PAÏDOUSSIS M P, SEMLER C. Dynamics of cantilevered pipes conveying fluid. Part 1:nonlinear equations of three-dimensional motion [J]. Journal of Fluids and Structures, 2007, 23(4): 545-567.

[ 4 ] PAÏDOUSSIS M P, GHAYESH M H. Three-dimensional dynamics of a cantilevered pipe conveying fluid, additionally supported by an intermediate spring array [J]. International Journal of Non-Linear Mechanics, 2010, 45(5): 507-524.

[ 5 ] MODARRES-SADEGHI Y, SEMLER C, WADHAM-GAGNON M, et al.Dynamics of cantilevered pipes conveying fluid. Part 3: three-dimensional dynamics in the presence of an end-mass [J]. Journal of Fluids and Structures, 2007, 23(4): 589-603.

[ 6 ] GHAYESH M H, PAÏDOUSSIS M P, MODARRES-SADEGHI Y. Three-dimensional dynamics of a fluid-conveying cantilevered pipe fitted with an additional spring-support and an end-mass [J]. Journal of Sound and Vibration, 2011, 330(12): 2869-2899.

[ 7 ] CHANG C H, MODARRES-SADEGHI Y. Flow-induced oscillations of a cantilevered pipe conveying fluid with base excitation [J]. Journal of Sound and Vibration, 2014, 333(18): 4265-4280.

[ 8 ] RINALDI S, PRABHAKAR S, VENGALLATORE S, et al. Dynamics of microscale pipes containing internal fluid flow: damping, frequency shift, and stability [J]. Journal of Sound and Vibration, 2010, 329(8): 1081-1088.

[ 9 ] NAJMZADEH M, HAASL S, ENOKSSON P. A silicon straight tube fluid density sensor [J]. Journal of Micromechanics and Microengineering, 2007, 17(8): 1657-1663.

[10] BHIRDE A A, PATEL V, GAVARD J, et al. Targeted killing of cancer cells in vivo and in vitro with EGT-directed carbon nanotube-based drug delivery [J]. ACS Nano, 2009, 3(2): 307-316.

[11] DELADI S, BERENSCHOT J W, TAS N R, et al. Fabrication of micromachined fountain pen with in situ characterization possibility of nanoscale surface modification [J]. Journal of Micromechanics and Microengineering, 2005, 15(3): 528-534.

[12] KIM K H, MOLDOVAN N, ESPINOSA H D. A nano fountain probe with sub-100 nm molecular writing resolution [J]. Small, 2005, 1(6): 632-635.

[13] FLECK N A, MULLER G M, ASHBY M F, et al. Strain gradient plasticity: Theory and experiment [J]. Acta Metallurgica et Materialia, 1994, 42(2): 475-487.

[14] LAM D C C, YANG F, CHONG A C M, et al. Experiments and theory in strain gradient elasticity [J]. Journal of the Mechanics and Physics of Solids, 2003, 51(8): 1477-1508.

[15] MCFARLAND A W, COLTON J S. Role of material microstructure in plate stiffness with relevance to microcantilever sensors [J]. Journal of Micromechanics and Microengineering, 2005, 15: 1060-1067.

[16] YANG F, CHONG A C M, LAM D C C, et al. Couple stress based strain gradient theory for elasticity [J]. International Journal of Solids and Structures, 2002, 39(10): 2731-2743.

[17] WANG Y G, LIN W H, LIU N. Nonlinear free vibration of a microscale beam based on modified couple stress theory [J]. Physica E, 2013, 47(Sup1): 80-85.

[18] DAI H L, WANG Y K, WANG L. Nonlinear dynamics of cantilevered microbeams based on modified couple stress theory [J]. International Journal of Engineering Science, 2015, 94: 103-112.

[19] MOHAMMAD-ABADI M, DANESHMEHR A R. Size dependent buckling analysis of microbeams based on modified couple stress theory with high order theories and general boundary conditions [J]. International Journal of Engineering Science, 2014, 74(1): 1-14.

[20] GHAYESH M H, FAROKHI H, ALICI G. Subcritical parametric dynamics of microbeams [J]. International Journal of Engineering Science, 2015, 95: 36-48.

[21] WANG L. Size-dependent vibration characteristics of fluid-conveying microtubes [J]. Journal of Fluids and Structures, 2010, 26(4): 675-684.

[22] XIA W, WANG L. Microfluid-induced vibration and stability of structures modeled as microscale pipes conveying fluid based on non-classical Timoshenko beam theory [J]. Microfluidics and Nanofluidics, 2010, 9(4/5): 955-962.

[23] WANG L, LIU H T, NI Q, et al. Flexural vibrations of microscale pipes conveying fluid by considering the size effects of micro-flow and micro-structure [J]. International Journal of Engineering Science, 2013, 71: 92-101.

[24] YANG T Z, JI S D, YANG X D, et al. Microfluid-induced nonlinear free vibration of microtubes [J]. International Journal of Engineering Science, 2014, 76: 47-55.

[25] HOSSEINI M, BAHAADINI R. Size dependent stability analysis of cantilever micro-pipes conveying fluid based on modified strain gradient theory [J]. International Journal of Engineering Science, 2016, 101(4): 1-13.

[26] BAHAADINI R, HOSSEINI M. Effects of nonlocal elasticity and slip condition on vibration and stability analysis of viscoelastic cantilever carbon nanotubes conveying fluid [J]. Computational Materials Science, 2016, 114: 151-159.

[27] TANG M, NI Q, WANG L, et al. Nonlinear modeling and size-dependent vibration analysis of curved microtubes conveying fluid based on modified couple stress theory [J]. International Journal of Engineering Science, 2014, 84(11): 1-10.

[28] BENJAMIN T B. Dynamics of a system of articulated pipes conveying fluid: I. Theory [J]. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, 1961, 261: 457-486.

[29] SEMLER C, LI G X, PAÏDOUSSIS M P. The non-linear equations of motion of pipes conveying fluid [J]. Journal of Sound and Vibration, 1994, 169(5): 577-599.

[30] LI G X, PAÏDOUSSIS M P. Stability, double degeneracy and chaos in cantilevered pipes conveying fluid [J]. International Journal of Non-Linear Mechanics, 1994, 29(1): 83-107.

Three-dimensionalflexuralvibrationofamicro-scalecantileverpipe-nonlinearequationsofmotionandscaleeffect

GUO Yong, XIE Jianhua

(School of Mechanics and Engineering, Southwest Jiaotong University, Chengdu 610031, China)

Flexural vibration of a micro-scale cantilever fluid-conveying pipe with annulus cross section can occur in each direction in the three-dimensional space. According to the Euler-Bernoulli beam theory, the displace components of the pipe and the relevant geometrical relations could be analyzed. The geometric nonlinearity, arising from the Lagrange strain tensor, was taken into account. Based on a modified couple stress theory, the strain energy in the pipe was calculated. The nonlinear dynamical equations of three-dimensional flexural vibration for a micro-scale cantilever fluid-conveying pipe were derived by using the Hamilton principle. The effect of the dimensionless material length scale parameter on the dynamics of the system was investigated. It is found that the scale effect increases the critical flow velocity of the pipe and that the larger the dimensionless material length scale parameter is, the wider (narrower) the region of stable planar (spatial) periodic motion is.

micro-scale cantilever pipe; three-dimensional flexural vibration; couple stress theory; Lagrange strain tensor; periodic motion

国家自然科学基金(11572263)

2016-10-18 修改稿收到日期： 2017-02-17

郭勇 男，博士生，1985年生

谢建华 男，博士，教授，1957年生

O322；O326

A

10.13465/j.cnki.jvs.2017.22.011